2022中考数学三轮冲刺考前提分微课06 隐圆问题
文档属性
| 名称 | 2022中考数学三轮冲刺考前提分微课06 隐圆问题 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 11:06:13 | ||
图片预览






文档简介
(共39张PPT)
2022年中考数学三轮复习(人教版)
提分微课 06
隐圆问题
●构图模型
●例题精析
●巩固训练
“隐圆”一般有如下呈现方式:①定点定长:当遇到同一个端点出发的等长线段时,通常以这个端点为圆心,等线段长为半径构造辅助圆;②定弦定角:当遇到动点对定线段所张的角为定值时,通常把张角转化为圆周角构造辅助圆.当遇到直角时,通常以斜边为直径构造辅助圆.“隐圆”常与线段最值结合考查.
构图模型
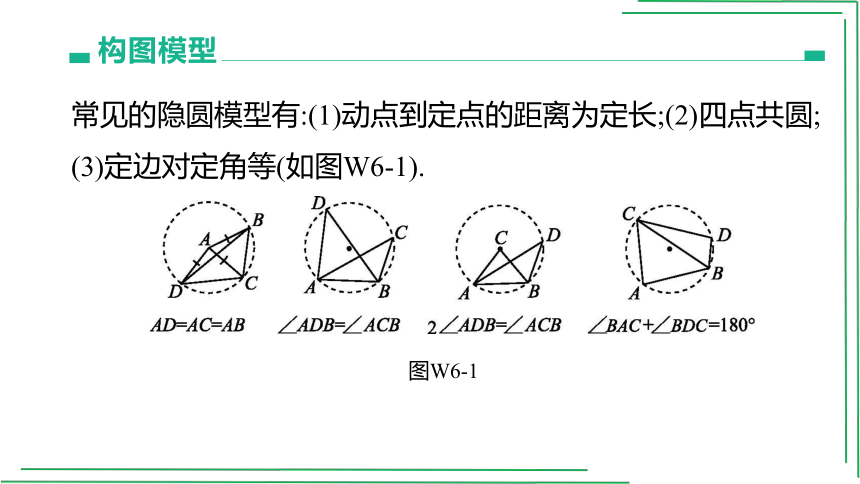
常见的隐圆模型有:(1)动点到定点的距离为定长;(2)四点共圆;
(3)定边对定角等(如图W6-1).
图W6-1
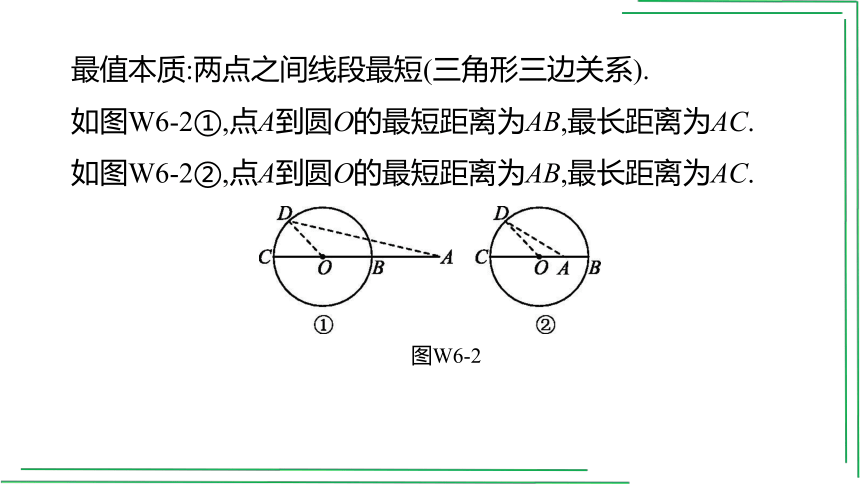
最值本质:两点之间线段最短(三角形三边关系).
如图W6-2①,点A到圆O的最短距离为AB,最长距离为AC.
如图W6-2②,点A到圆O的最短距离为AB,最长距离为AC.
图W6-2
例题精析
例1 如图W6-3,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 .
图W6-3
[例1思路分析]△CEF沿直线EF翻折时,点F为定点,∵CF=PF,∴PF为定线,即点P在以F为圆心,PF长为半径的圆弧上运动.——转化为圆上一点到直线的最短距离问题.
1.2
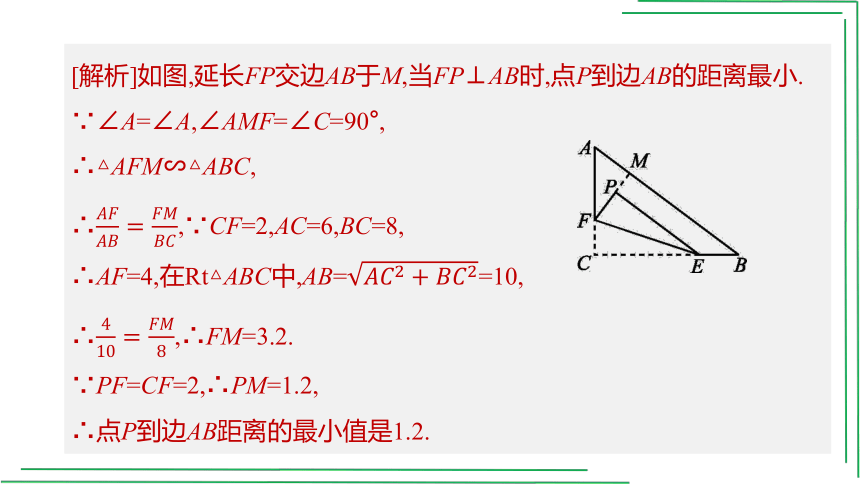
[解析]如图,延长FP交边AB于M,当FP⊥AB时,点P到边AB的距离最小.
∵∠A=∠A,∠AMF=∠C=90°,
∴△AFM∽△ABC,
∴,∵CF=2,AC=6,BC=8,
∴AF=4,在Rt△ABC中,AB==10,
∴,∴FM=3.2.
∵PF=CF=2,∴PM=1.2,
∴点P到边AB距离的最小值是1.2.
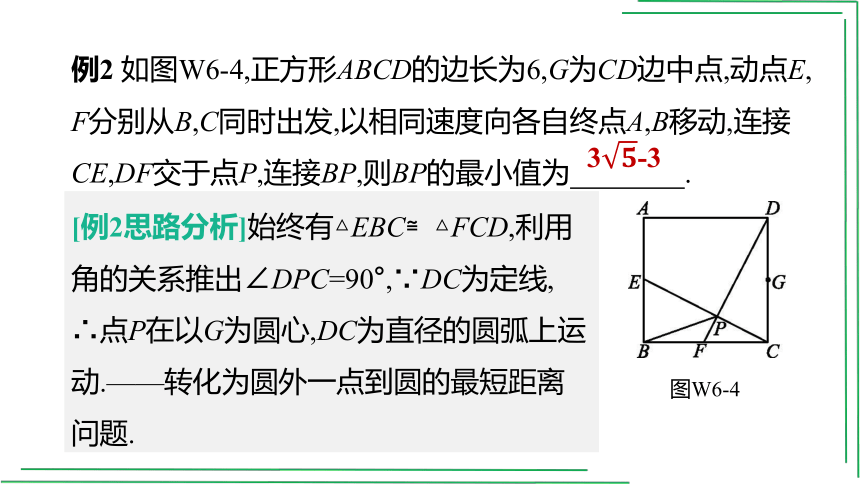
例2 如图W6-4,正方形ABCD的边长为6,G为CD边中点,动点E,
F分别从B,C同时出发,以相同速度向各自终点A,B移动,连接CE,DF交于点P,连接BP,则BP的最小值为 .
图W6-4
[例2思路分析]始终有△EBC≌△FCD,利用角的关系推出∠DPC=90°,∵DC为定线,
∴点P在以G为圆心,DC为直径的圆弧上运动.——转化为圆外一点到圆的最短距离问题.
3-3
[解析]连接BG,由题可知BE=CF,∠EBC=∠DCF,BC=DC,
∴△EBC≌△FCD,∴∠ECB=∠FDC.
∵∠ECB+∠DCP=90°,
∴∠FDC+∠DCP=90°,即∠DPC=90°,
∴点P在以DC为直径的圆上运动,
∴当B,P,G三点共线时,BP长度最小.
在Rt△BCG中,由勾股定理可知BG==3,
∴BP的最小值为3-3.
例3 如图W6-5,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A'MN,连接A'C,则线段A'C长度的最小值是 .
图W6-5
[例3思路分析]△AMN沿MN所在直线翻折得到△A'MN,可得MA'=MA=2,即点A'在以M点为圆心,MA为半径的圆弧上运动.——转化为圆外一点到圆的最短距离问题.
2-2
[解析]如图所示, ∵在N的运动过程中,A'在以M为圆心,MA的长为半径的圆上运动,
∴MA'是定值,A'C长度取最小值时,A'在MC上.
过点M作MF⊥DC交CD延长线于点F,
∵在边长为4的菱形ABCD中,∠A=60°,M为AD中点,
∴MD=2,∠FDM=60°,∴∠FMD=30°,∴FD=MD=1,FM=DM·cos30°=,CF=FD+DC=5,∴在Rt△MFC中,MC==2,
∴A'C=MC-MA'=2-2.故答案为:2-2.
巩固训练
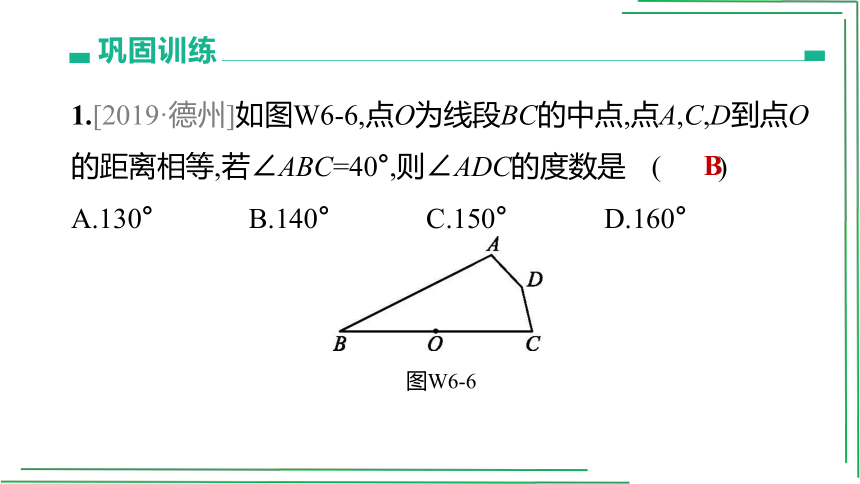
1.[2019·德州]如图W6-6,点O为线段BC的中点,点A,C,D到点O的距离相等,若∠ABC=40°,则∠ADC的度数是 ( )
A.130° B.140° C.150° D.160°
图W6-6
B
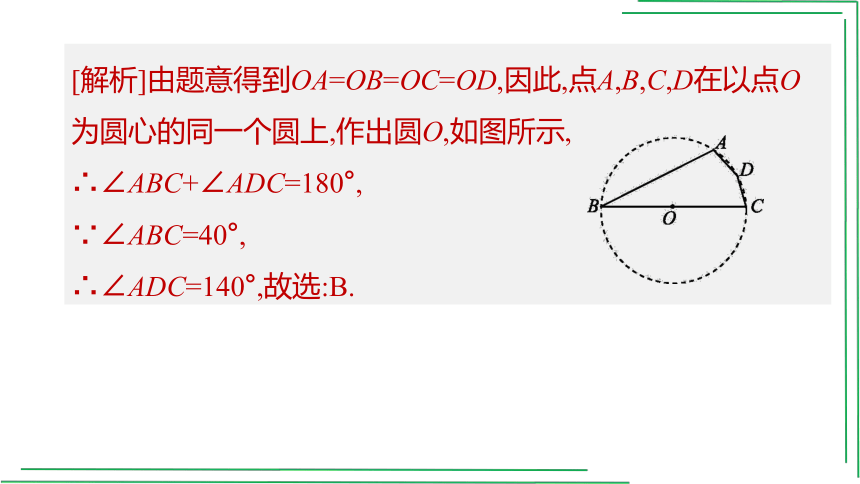
[解析]由题意得到OA=OB=OC=OD,因此,点A,B,C,D在以点O为圆心的同一个圆上,作出圆O,如图所示,
∴∠ABC+∠ADC=180°,
∵∠ABC=40°,
∴∠ADC=140°,故选:B.
2.如图W6-7,在四边形ABCD中,AB=AC=AD,若∠BAC=25°,
∠CAD=75°,则∠BDC= °,∠DBC= °.
图W6-7
12.5
37.5
3.如图W6-8,在矩形ABCD中,AB=8,BC=6,将点D沿过A点的直线折叠,点D的对称点为D',则线段CD'的最小值为 .
图W6-8
4
[解析]连接AC.∵四边形ABCD是矩形,
∴AD=BC=6,∠B=90°.
∵AB=8,BC=6,∴AC==10.
由折叠的性质知AD=AD'=6,
∴点D'在以点A为圆心,AD长为半径的圆上,
∴当点D'在线段AC上时,CD'最小,
∴CD'的最小值=10-6=4.
4.如图W6-9,在△ABC中,∠ABC=90°,AB=6,BC=8,点P为△ABC内部一动点,且∠PAB=∠PBC,连接CP,则CP的最小值为
.
图W6-9
-3
[解析]∵∠ABC=90°,∴∠ABP+∠PBC=90°.
∵∠PAB=∠PBC,∴∠BAP+∠ABP=90°,∴∠APB=90°,
∴点P在以AB为直径的☉O上,连接OC交☉O于点P,此时PC最小,
∴OP=OA=OB,
在Rt△BCO中,
∵∠OBC=90°,BC=8,OB=3,
∴OC=.
∴PC=OC-OP=-3.∴PC最小值为-3.
5.如图W6-10,正方形ABCD的边长是4,点E是AD边上一动点,连接BE,过点A作AF⊥BE于点F,点P是AD边上另一动点,则PC+PF的最小值为 .
图W6-10
2-2
[解析]∠AFB=90°且AB是定线段,故F点轨迹是以AB中点O为圆心、AB为直径的圆弧.考虑PC+PF是折线段,作点C关于AD的对称点C',化PC+PF为PC'+PF,当C',P,F,O共线时,取到最小值.易知C'O==2,
所以C'F=2-2.
所以PC+PF的最小值为2-2.
6.[2019·南京]在△ABC中,AB=4,∠C=60°,∠A>∠B,则BC长的取值范围是 .
4[解析]作△ABC的外接圆,如图所示.
∵∠BAC>∠ABC,AB=4,
∴当∠BAC=90°,BC是直径时最长,
∵∠C=60°,
∴AC=,BC=;
当∠BAC=∠ABC时,△ABC是等边三角形,BC1=AB=4,
∵∠BAC>∠ABC,
∴BC长的取值范围是4故答案为:47.如图W6-11,在等腰直角三角形ABC中,AB=BC=2,点P为等腰直角三角形ABC所在平面内一点,且满足PA⊥PB,则PC的取值范围为 .
图W6-11
-1≤PC≤+1
[解析]根据条件可知线段AB是定值,
且AB所对的张角∠APB是定值.根据
同弧所对的圆周角相等可知,动点P的
运动轨迹在过点A,B,P三点的圆周上(不与A,B重合).又因为∠APB=90°,所以AB恰好是直径,设AB中点为O,以O为圆心,OA为半径作圆,连接CO并延长交圆O于点P1,P2.CP1最小,CP2最大,所以PC的取值范围为-1≤PC≤+1.
8.[2020·徐州]在△ABC中,若AB=6,∠ACB=45°,则△ABC面积的最大值为
.
9+9
[解析]以AB为斜边向上作等腰直角三角形OAB,
∵AB=6,∴OA=3,以O为圆心,OA为半径画圆,
由于∠ACB=45°=∠AOB,∴点C在☉O上,过点O
作OD⊥AB,垂足为D,∴OD=AB=3,当点C在DO的延长线上时,
△ABC的面积最大,最大面积为AB×CD=×6×(3+3)=9+9.
9.如图W6-12,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为 .
图W6-12
[解析]连接AC,过G作GH⊥AC于H,
∵四边形ABCD是矩形,
∴CD=AB=3,AD=BC=4,∠ABC=∠D=90°,
根据勾股定理得,AC=5,
∵AB=3,AE=2,
∴点F在BC上的任何位置时,
点G始终在AC的下方,
设点G到AC的距离为h,
∵=S△ACD+S△ACG=AD×CD+AC×h=×4×3+×5×h
=h+6,
∴h最小时,四边形AGCD的面积最小,
∵点G是以点E为圆心,BE=1为半径的圆弧上的点,
∴EG⊥AC时,h最小,
在Rt△ABC中,sin∠BAC=,
在Rt△AEH中,AE=2,sin∠BAC=,
∴EH=AE=,∴h=EH-EG=-1=,
∴h+6=+6=.
10.如图W6-13,在平面直角坐标系中,直线y=kx(k≠0)经过点(a,a)(a>0),线段BC的两个端点分别在x轴与直线y=kx上(点B,C均与原点O不重合)滑动,且BC=2,分别作BP⊥x轴,CP⊥直线y=kx,交点为P.经探究,在整个滑动过程中,P,O两点间的距离
为定值 .
图W6-13
[解析]如图,连接OP,取OP的中点D,连接CD,BD.
因为CP⊥直线y=kx,BP⊥x轴,
所以∠PCO=∠PBO=90°,
所以OD=DP=CD=BD.
所以O,B,P,C四点共圆,OP为直径.
因为直线y=kx(k≠0)经过点(a,a),
所以tan∠BOC=,
所以∠BOC=60°.
所以∠BDC=2∠BOC=120°.
过点D作DE⊥BC于点E.
所以BE=BC=1,∠BDE=∠BDC=60°.
在Rt△BDE中,sin∠BDE=,所以BD=,所以OP=2BD=.
11.如图W6-14,已知正方形ABCD的边长为4,点P是AB边上的一个动点,连接CP,过点P作PC的垂线交AD于点E,以PE为边作正方形PEFG,顶点G在线段PC上,对角线EG,PF相交于点O.
(1)若AP=1,则AE= .
(2)①求证:点O一定在△APE的外接圆上;
②当点P从点A运动到点B时,点O也随之
运动,求点O经过的路径长.
(3)在点P从点A到点B的运动过程中,△APE的外接圆的圆心也随之运动,求该圆心到AB边的距离的最大值.
图W6-14
(1)若AP=1,则AE= .
图W6-14
[解析]∵四边形ABCD、四边形PEFG是正方形,
∴∠A=∠B=∠EPG=90°,PF⊥EG,AB=BC=4,
∴∠AEP+∠APE=90°,∠BPC+∠APE=90°,
∴∠AEP=∠BPC,∴△APE∽△BCP,
∴,即,解得AE=.
(2)①求证:点O一定在△APE的外接圆上;
②当点P从点A运动到点B时,点O也随之运动,求点O经过的路径长.
图W6-14
解:(2)①证明:∵PF⊥EG,∴∠EOP=90°,
∴∠EOP+∠A=180°,∴A,P,O,E四点共圆,
∴点O一定在△APE的外接圆上.
②连接OA,AC,
如图①所示.
∵四边形ABCD是正方形,∴∠B=90°,∠BAC=45°,
∴AC==4,
∵A,P,O,E四点共圆,
∴∠OAP=∠OEP=45°,
∴点O在AC上,
当P运动到点B时,O为AC的中点,OA=AC=2,
即点O经过的路径长为2.
(3)在点P从点A到点B的运动过程中,△APE的外接圆的圆心也随之运动,求该圆心到AB边的距离的最大值.
图W6-14
(3)设△APE的外接圆的圆心为M,
作MN⊥AB于N,如图②所示,
则MN∥AE,
∵ME=MP,
∴AN=PN,
∴MN=AE,
设AP=x,则BP=4-x,
由(1)得△APE∽△BCP,∴,
即,
解得AE=x-x2=-(x-2)2+1,
∴x=2时,AE的最大值为1,
此时MN的最大值=×1=,
即△APE的外接圆的圆心到AB边的距离的最大值为.
https://www.21cnjy.com/help/help_extract.php
2022年中考数学三轮复习(人教版)
提分微课 06
隐圆问题
●构图模型
●例题精析
●巩固训练
“隐圆”一般有如下呈现方式:①定点定长:当遇到同一个端点出发的等长线段时,通常以这个端点为圆心,等线段长为半径构造辅助圆;②定弦定角:当遇到动点对定线段所张的角为定值时,通常把张角转化为圆周角构造辅助圆.当遇到直角时,通常以斜边为直径构造辅助圆.“隐圆”常与线段最值结合考查.
构图模型
常见的隐圆模型有:(1)动点到定点的距离为定长;(2)四点共圆;
(3)定边对定角等(如图W6-1).
图W6-1
最值本质:两点之间线段最短(三角形三边关系).
如图W6-2①,点A到圆O的最短距离为AB,最长距离为AC.
如图W6-2②,点A到圆O的最短距离为AB,最长距离为AC.
图W6-2
例题精析
例1 如图W6-3,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 .
图W6-3
[例1思路分析]△CEF沿直线EF翻折时,点F为定点,∵CF=PF,∴PF为定线,即点P在以F为圆心,PF长为半径的圆弧上运动.——转化为圆上一点到直线的最短距离问题.
1.2
[解析]如图,延长FP交边AB于M,当FP⊥AB时,点P到边AB的距离最小.
∵∠A=∠A,∠AMF=∠C=90°,
∴△AFM∽△ABC,
∴,∵CF=2,AC=6,BC=8,
∴AF=4,在Rt△ABC中,AB==10,
∴,∴FM=3.2.
∵PF=CF=2,∴PM=1.2,
∴点P到边AB距离的最小值是1.2.
例2 如图W6-4,正方形ABCD的边长为6,G为CD边中点,动点E,
F分别从B,C同时出发,以相同速度向各自终点A,B移动,连接CE,DF交于点P,连接BP,则BP的最小值为 .
图W6-4
[例2思路分析]始终有△EBC≌△FCD,利用角的关系推出∠DPC=90°,∵DC为定线,
∴点P在以G为圆心,DC为直径的圆弧上运动.——转化为圆外一点到圆的最短距离问题.
3-3
[解析]连接BG,由题可知BE=CF,∠EBC=∠DCF,BC=DC,
∴△EBC≌△FCD,∴∠ECB=∠FDC.
∵∠ECB+∠DCP=90°,
∴∠FDC+∠DCP=90°,即∠DPC=90°,
∴点P在以DC为直径的圆上运动,
∴当B,P,G三点共线时,BP长度最小.
在Rt△BCG中,由勾股定理可知BG==3,
∴BP的最小值为3-3.
例3 如图W6-5,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A'MN,连接A'C,则线段A'C长度的最小值是 .
图W6-5
[例3思路分析]△AMN沿MN所在直线翻折得到△A'MN,可得MA'=MA=2,即点A'在以M点为圆心,MA为半径的圆弧上运动.——转化为圆外一点到圆的最短距离问题.
2-2
[解析]如图所示, ∵在N的运动过程中,A'在以M为圆心,MA的长为半径的圆上运动,
∴MA'是定值,A'C长度取最小值时,A'在MC上.
过点M作MF⊥DC交CD延长线于点F,
∵在边长为4的菱形ABCD中,∠A=60°,M为AD中点,
∴MD=2,∠FDM=60°,∴∠FMD=30°,∴FD=MD=1,FM=DM·cos30°=,CF=FD+DC=5,∴在Rt△MFC中,MC==2,
∴A'C=MC-MA'=2-2.故答案为:2-2.
巩固训练
1.[2019·德州]如图W6-6,点O为线段BC的中点,点A,C,D到点O的距离相等,若∠ABC=40°,则∠ADC的度数是 ( )
A.130° B.140° C.150° D.160°
图W6-6
B
[解析]由题意得到OA=OB=OC=OD,因此,点A,B,C,D在以点O为圆心的同一个圆上,作出圆O,如图所示,
∴∠ABC+∠ADC=180°,
∵∠ABC=40°,
∴∠ADC=140°,故选:B.
2.如图W6-7,在四边形ABCD中,AB=AC=AD,若∠BAC=25°,
∠CAD=75°,则∠BDC= °,∠DBC= °.
图W6-7
12.5
37.5
3.如图W6-8,在矩形ABCD中,AB=8,BC=6,将点D沿过A点的直线折叠,点D的对称点为D',则线段CD'的最小值为 .
图W6-8
4
[解析]连接AC.∵四边形ABCD是矩形,
∴AD=BC=6,∠B=90°.
∵AB=8,BC=6,∴AC==10.
由折叠的性质知AD=AD'=6,
∴点D'在以点A为圆心,AD长为半径的圆上,
∴当点D'在线段AC上时,CD'最小,
∴CD'的最小值=10-6=4.
4.如图W6-9,在△ABC中,∠ABC=90°,AB=6,BC=8,点P为△ABC内部一动点,且∠PAB=∠PBC,连接CP,则CP的最小值为
.
图W6-9
-3
[解析]∵∠ABC=90°,∴∠ABP+∠PBC=90°.
∵∠PAB=∠PBC,∴∠BAP+∠ABP=90°,∴∠APB=90°,
∴点P在以AB为直径的☉O上,连接OC交☉O于点P,此时PC最小,
∴OP=OA=OB,
在Rt△BCO中,
∵∠OBC=90°,BC=8,OB=3,
∴OC=.
∴PC=OC-OP=-3.∴PC最小值为-3.
5.如图W6-10,正方形ABCD的边长是4,点E是AD边上一动点,连接BE,过点A作AF⊥BE于点F,点P是AD边上另一动点,则PC+PF的最小值为 .
图W6-10
2-2
[解析]∠AFB=90°且AB是定线段,故F点轨迹是以AB中点O为圆心、AB为直径的圆弧.考虑PC+PF是折线段,作点C关于AD的对称点C',化PC+PF为PC'+PF,当C',P,F,O共线时,取到最小值.易知C'O==2,
所以C'F=2-2.
所以PC+PF的最小值为2-2.
6.[2019·南京]在△ABC中,AB=4,∠C=60°,∠A>∠B,则BC长的取值范围是 .
4
∵∠BAC>∠ABC,AB=4,
∴当∠BAC=90°,BC是直径时最长,
∵∠C=60°,
∴AC=,BC=;
当∠BAC=∠ABC时,△ABC是等边三角形,BC1=AB=4,
∵∠BAC>∠ABC,
∴BC长的取值范围是4
图W6-11
-1≤PC≤+1
[解析]根据条件可知线段AB是定值,
且AB所对的张角∠APB是定值.根据
同弧所对的圆周角相等可知,动点P的
运动轨迹在过点A,B,P三点的圆周上(不与A,B重合).又因为∠APB=90°,所以AB恰好是直径,设AB中点为O,以O为圆心,OA为半径作圆,连接CO并延长交圆O于点P1,P2.CP1最小,CP2最大,所以PC的取值范围为-1≤PC≤+1.
8.[2020·徐州]在△ABC中,若AB=6,∠ACB=45°,则△ABC面积的最大值为
.
9+9
[解析]以AB为斜边向上作等腰直角三角形OAB,
∵AB=6,∴OA=3,以O为圆心,OA为半径画圆,
由于∠ACB=45°=∠AOB,∴点C在☉O上,过点O
作OD⊥AB,垂足为D,∴OD=AB=3,当点C在DO的延长线上时,
△ABC的面积最大,最大面积为AB×CD=×6×(3+3)=9+9.
9.如图W6-12,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为 .
图W6-12
[解析]连接AC,过G作GH⊥AC于H,
∵四边形ABCD是矩形,
∴CD=AB=3,AD=BC=4,∠ABC=∠D=90°,
根据勾股定理得,AC=5,
∵AB=3,AE=2,
∴点F在BC上的任何位置时,
点G始终在AC的下方,
设点G到AC的距离为h,
∵=S△ACD+S△ACG=AD×CD+AC×h=×4×3+×5×h
=h+6,
∴h最小时,四边形AGCD的面积最小,
∵点G是以点E为圆心,BE=1为半径的圆弧上的点,
∴EG⊥AC时,h最小,
在Rt△ABC中,sin∠BAC=,
在Rt△AEH中,AE=2,sin∠BAC=,
∴EH=AE=,∴h=EH-EG=-1=,
∴h+6=+6=.
10.如图W6-13,在平面直角坐标系中,直线y=kx(k≠0)经过点(a,a)(a>0),线段BC的两个端点分别在x轴与直线y=kx上(点B,C均与原点O不重合)滑动,且BC=2,分别作BP⊥x轴,CP⊥直线y=kx,交点为P.经探究,在整个滑动过程中,P,O两点间的距离
为定值 .
图W6-13
[解析]如图,连接OP,取OP的中点D,连接CD,BD.
因为CP⊥直线y=kx,BP⊥x轴,
所以∠PCO=∠PBO=90°,
所以OD=DP=CD=BD.
所以O,B,P,C四点共圆,OP为直径.
因为直线y=kx(k≠0)经过点(a,a),
所以tan∠BOC=,
所以∠BOC=60°.
所以∠BDC=2∠BOC=120°.
过点D作DE⊥BC于点E.
所以BE=BC=1,∠BDE=∠BDC=60°.
在Rt△BDE中,sin∠BDE=,所以BD=,所以OP=2BD=.
11.如图W6-14,已知正方形ABCD的边长为4,点P是AB边上的一个动点,连接CP,过点P作PC的垂线交AD于点E,以PE为边作正方形PEFG,顶点G在线段PC上,对角线EG,PF相交于点O.
(1)若AP=1,则AE= .
(2)①求证:点O一定在△APE的外接圆上;
②当点P从点A运动到点B时,点O也随之
运动,求点O经过的路径长.
(3)在点P从点A到点B的运动过程中,△APE的外接圆的圆心也随之运动,求该圆心到AB边的距离的最大值.
图W6-14
(1)若AP=1,则AE= .
图W6-14
[解析]∵四边形ABCD、四边形PEFG是正方形,
∴∠A=∠B=∠EPG=90°,PF⊥EG,AB=BC=4,
∴∠AEP+∠APE=90°,∠BPC+∠APE=90°,
∴∠AEP=∠BPC,∴△APE∽△BCP,
∴,即,解得AE=.
(2)①求证:点O一定在△APE的外接圆上;
②当点P从点A运动到点B时,点O也随之运动,求点O经过的路径长.
图W6-14
解:(2)①证明:∵PF⊥EG,∴∠EOP=90°,
∴∠EOP+∠A=180°,∴A,P,O,E四点共圆,
∴点O一定在△APE的外接圆上.
②连接OA,AC,
如图①所示.
∵四边形ABCD是正方形,∴∠B=90°,∠BAC=45°,
∴AC==4,
∵A,P,O,E四点共圆,
∴∠OAP=∠OEP=45°,
∴点O在AC上,
当P运动到点B时,O为AC的中点,OA=AC=2,
即点O经过的路径长为2.
(3)在点P从点A到点B的运动过程中,△APE的外接圆的圆心也随之运动,求该圆心到AB边的距离的最大值.
图W6-14
(3)设△APE的外接圆的圆心为M,
作MN⊥AB于N,如图②所示,
则MN∥AE,
∵ME=MP,
∴AN=PN,
∴MN=AE,
设AP=x,则BP=4-x,
由(1)得△APE∽△BCP,∴,
即,
解得AE=x-x2=-(x-2)2+1,
∴x=2时,AE的最大值为1,
此时MN的最大值=×1=,
即△APE的外接圆的圆心到AB边的距离的最大值为.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
