2022中考数学三轮冲刺考前提分微课08 PA±PB型最值问题 课件(共39张PPT)
文档属性
| 名称 | 2022中考数学三轮冲刺考前提分微课08 PA±PB型最值问题 课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 11:00:30 | ||
图片预览









文档简介
(共39张PPT)
2022年中考数学三轮复习(人教版)
提分微课 08
PA±PB型最值问题
●构图模型
●例题精析
●巩固训练
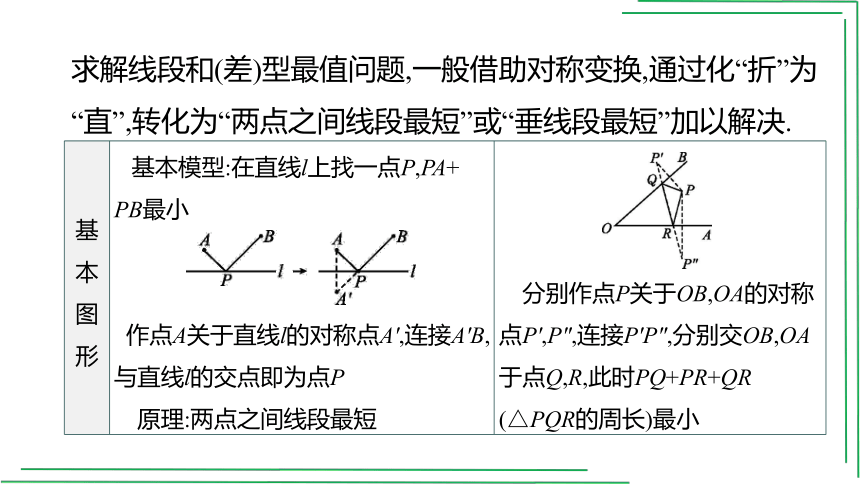
求解线段和(差)型最值问题,一般借助对称变换,通过化“折”为“直”,转化为“两点之间线段最短”或“垂线段最短”加以解决.
基本 图形 基本模型:在直线l上找一点P,PA+ PB最小 作点A关于直线l的对称点A',连接A'B,与直线l的交点即为点P 原理:两点之间线段最短
分别作点P关于OB,OA的对称点P',P″,连接P'P″,分别交OB,OA于点Q,R,此时PQ+PR+QR
(△PQR的周长)最小
(续表)
基本 图形 考虑到PQ为定值,故当QM +MN+NP最小时,PQ+MQ+MN +PN(四边形PQMN的周长)最小.类似地,当P',N,M,Q'共线时取最小值 在OA,OB上分别取点M,N,使得PM+
MN最小(垂线段最短)
此处M为“折点”,作点P关于OA的对称点P',则PM+MN=P'M+MN.过点P'作OB的垂线,与OA,OB的交点即为满足条件的M,N
原理:垂线段最短
(续表)
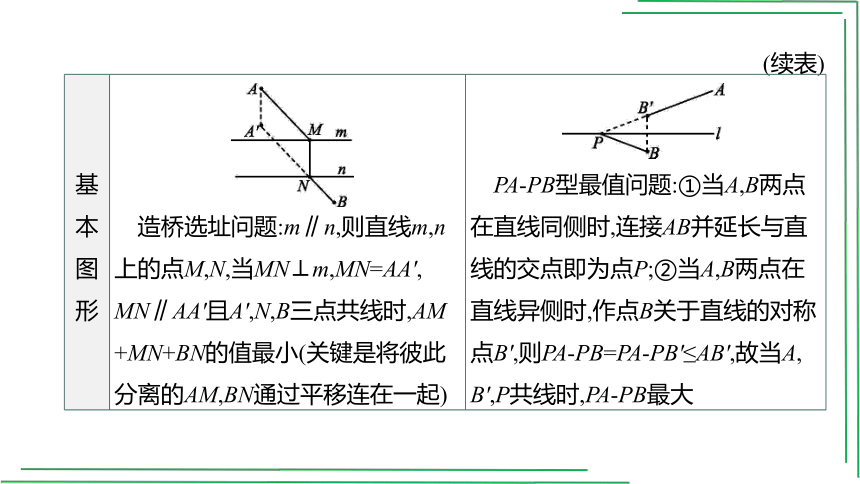
基本 图形 造桥选址问题:m∥n,则直线m,n上的点M,N,当MN⊥m,MN=AA', MN∥AA'且A',N,B三点共线时,AM +MN+BN的值最小(关键是将彼此分离的AM,BN通过平移连在一起)
PA-PB型最值问题:①当A,B两点在直线同侧时,连接AB并延长与直线的交点即为点P;②当A,B两点在直线异侧时,作点B关于直线的对称点B',则PA-PB=PA-PB'≤AB',故当A,
B',P共线时,PA-PB最大
(续表)
总结 求解此类问题的关键是构造对称.构图原则:同侧化异侧,折线变直线
例题精析
例 (1)如图W8-1①,正方形ABCD的边长为8,M在DC上,且DM=
2,N是AC上一动点,则DN+MN的最小值为 .
图W8-1
10
[解析]如图①,由条件易知,B,D关于直线AC对称,连接BM,则BM的长为DN+NM的最小值.
在直角三角形BCM中,BC=8,CM=8-2=6,
则BM==10.
例 (2)如图②,点A是半圆上(半径为1)的三等分点,B是的中点,P是直径MN上一动点,则PA+PB的最小值为 .
图W8-1
[解析]如图②,作B关于MN的对称点C,则C在圆上.连接AC,OC,则AC的长就是AP+BP的最小值.
∵∠AOC=∠AON+∠NOC=60°+30°=90°,
∴△AOC是等腰直角三角形,
∴AC=OA=,
即AP+BP的最小值是.
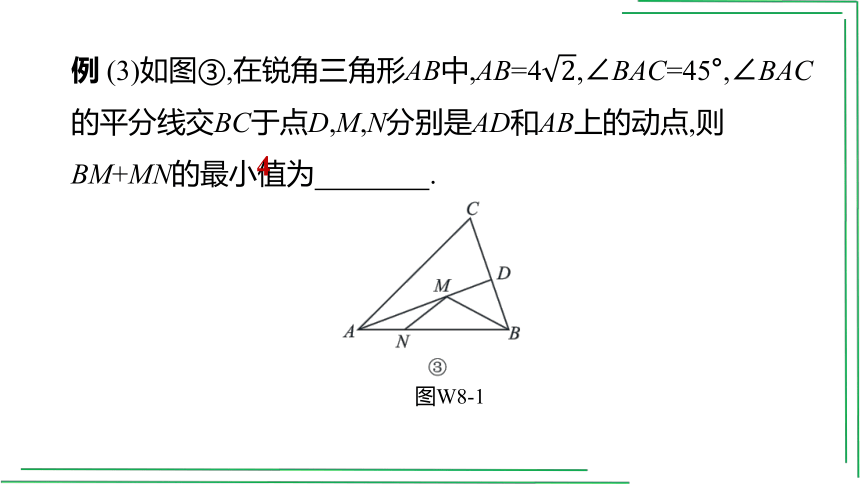
例 (3)如图③,在锐角三角形AB中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值为 .
图W8-1
4
[解析]如图③,作点N关于AD的对称点N',作BH⊥AC于H.
∵BM+MN=BM+MN',BM+MN'≥BH,
∴BH的长就是BM+MN的最小值.
∵∠BAC=45°,∴△ABH是等腰直角三角形,
∴BH=×4=4.
[思路分析]
求解时,首先分析求最值的线段中涉及几个动点、几个定点,再根据上面的类型转化求解.如(3)中,对于BM+MN,M,N是动点,B是定点,作点N关于直线AD的对称点N',则BM+MN=BM+
MN',所以当B,M,N'三点共线,即BN'⊥AC时,BM+MN取最小值.
巩固训练
1.如图W8-2,点P是边长为2的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边的中点,则MP+PN的最小值是 ( )
A.1 B.2 C.2 D.4
图W8-2
B
[解析]如图,作点M关于AC的对称点M',连接M'N交AC于P,此时MP+NP有最小值,最小值为M'N的长.
∵菱形ABCD关于AC对称,M是AB边的中点,
∴M'是AD的中点.
又∵N是BC边的中点,∴AM'∥BN,AM'=BN,
∴四边形ABNM'是平行四边形,∴M'N=AB=2,
即MP+NP的最小值为2.故选B.
2.如图W8-3,在等边三角形ABC中,AB=6,AD⊥BC,E是AC上的一点,M是AD上的一点,且AE=2,则ME+MC的最小值为 ( )
A. B.3 C.2 D.4
图W8-3
C
[解析]设点C关于直线AD的对称点是点B,连接BE,交AD于点M,
此时ME+MC的值最小.
过点B作BH⊥AC于点H,此时CH=AH=AC=3,
则EH=AH-AE=3-2=1,
BH==3.
在Rt△BHE中,BE==2,
即ME+MC的最小值为2.故选C.
3.如图W8-4,在Rt△AOB中,∠AOB=90°,OA=3,OB=4,以点O为圆心,2为半径的圆与OB交于点C,过点C作CD⊥OB交AB于点D,点P是边OA上的动点.当PC+PD最小时,OP的长为 ( )
A. B. C.1 D.
图W8-4
B
[解析]如图,延长CO交☉O于点E,连接ED,交AO于点P,此时PC+PD的值最小.
∵CD⊥OB,∴∠DCB=90°.
又∠AOB=90°,∴∠DCB=∠AOB,∴CD∥AO,∴.
∵OC=2,OB=4,∴BC=2,∴,解得CD=.
∵CD∥AO,∴,即,解得PO=.
故选B.
4.如图W8-5,在矩形ABCD中,AD=4,∠DAC=30°,点P,E分别在AC,AD上,则PE+PD的最小值是 .
图W8-5
2
[解析]如图,作点D关于直线AC的对称点D',当D',P,E三点共线,且D'E⊥AD时,PE+PD最小,易得CD=,
∠ADD'=60°,
DD'=4,所以D'E=2.
5.如图W8-6,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为 .
图W8-6
[解析]如图,作点P关于BD的对称点P',
则PK+QK=P'K+QK.当P',K,Q三点共线,且P'Q⊥CD时,
PK+QK取得最小值.
过点A作AE⊥CD于点E.
∵在菱形ABCD中,AB=AD=2,∠BAD=120°,
∴∠ADC=60°,∴AE=AD·sin∠ADC=2×,
∵P'Q⊥CD,AE⊥CD,AB∥CD,∴P'Q=AE=.
∴PK+QK的最小值为.
6.如图W8-7,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=S矩形ABCD,则点P到A,B两点的距离之和PA+PB的最小值为 .
图W8-7
4
[解析]如图,设△PAB中AB边上的高是h,
∵S△PAB=S矩形ABCD,∴AB·h=AB·AD,
∴h=AD=2,∴动点P在与AB平行且与
AB的距离是2的线段l(线段l的长度为4,且点P不过线段l与AD,BC的交点)上,如图,作点A关于直线l的对称点A',连接AA',BA',交l于P',则BA'即为所求的最短距离.
在Rt△ABA'中,AB=4,AA'=2+2=4,
∴BA'==4,即PA+PB的最小值为4.
7.如图W8-8,正比例函数y=x的图象与反比例函数y=在第一象限的图象交于A点,点B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,点P为x轴上一点,当PA+PB的值最小时,点P的
坐标为 .
图W8-8
(,0)
[解析]联立得解得∴A(2,1).
设A点关于x轴的对称点为C,
则C点的坐标为(2,-1).
连接BC交x轴于点P,此时PA+PB的值最小,如图所示.
设直线BC的解析式为y=mx+n.
易知B点坐标为(1,2),
将B和C的坐标代入得解得
∴BC的解析式为y=-3x+5.
当y=0时,x=,∴P点坐标为(,0).
8.如图W8-9,抛物线y=x2+2x-3与x轴交于A,B两点,与y轴交于点C,点P是抛物线对称轴上任意一点,若点D,E,F分别是BC,BP,
PC的中点,连接DE,DF,则DE+DF的最小值为 .
图W8-9
[解析]因为点D,E,F分别是BC,BP,PC的中点,所以DE,DF是△PBC的中位线,所以DE=PC,DF=PB,所以DE+DF=(PC+PB),故本题可转化为求PC+PB的最小值,因为B,C为定点,P为对称轴上一动点,点A,B关于对称轴对称,所以连接AC,PC+PB的最小值等于AC的长度,由抛物线解析式可得A(-3,0),C(0,-3),
∴AC=3,DE+DF的最小值=AC=.
9.如图W8-10,四边形ABCD中,∠C=50°,∠B=∠D=90°,E,F分别是BC,DC上的动点,当△AEF的周长最小时,∠EAF的度数为
.
图W8-10
80°
[解析]如图,分别作A关于BC和CD的对称点A',A″,连接A'A″,交BC于E,交CD于F,则A'A″的长即为△AEF周长的最小值.作DA延长线AH,易知∠DAB=130°,∠HAA'=50°.
又∠EA'A=∠EAA',∠FAD=∠A″,
且∠EA'A+∠EAA'=∠AEF,∠FAD+∠A″=∠AFE,
所以∠AEF+∠AFE=∠EA'A+∠EAA'+∠FAD+∠A″
=2(∠AA'E+∠A″)=2∠HAA'=100°,
所以∠EAF=180°-100°=80°.
10.[2019·陕西]如图W8-11,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6.P为对角线BD上一点,则PM-PN的最大值为 .
图W8-11
2
[解析]作点M关于BD的对称点M',根据对称性可知M'在AB上且AM'=2,连接PM',则PM'=PM,∴PM-PN=PM'-PN≤M'N,
当M',N,P共线时,此时PM'-PN=M'N,取得最大值.
∵,∴△AM'N∽△ABC,
即△AM'N是等腰直角三角形,
∴M'N=AM'=2,
∴PM-PN的最大值为2.
11.如图W8-12,已知直线l1∥l2,l1,l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ=4,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ最小,此时PA+BQ= .
图W8-12
16
[解析]作PE⊥l1于E,交l2于F,在PF上截取PC=8,连接QC交l2于B,此时PA+AB+BQ最短.作QD⊥PF交PF的延长线于D.
在Rt△PQD中,∵∠D=90°,PQ=4,PD=18,
∴DQ=,CD=PD-PC=18-8=10.
∵AB=PC=8,AB∥PC,
∴四边形ABCP是平行四边形,∴PA=BC,
∴PA+BQ=CB+BQ=QC==16.
故答案为16.
12.如图W8-13,已知菱形ABCD的对角线AC,BD相交于点O,
AC=6,BD=8,点E在AD上,,点F为AB的中点,点G,H为BD上的动点,GH=1,连接FH,EG,则FH+EG的最小值为 .
图W8-13
[解析]∵四边形ABCD是菱形,∴AC⊥BD,
∴∠AOD=90°,OB=OD,OC=OA,
∵AC=6,BD=8,∴OA=3,OB=4,
作F关于DB的对称点F',作EE'⊥OA于E',
∴EE'∥OD,∴△AE'E∽△AOD,
∴,∴EE'=1,
连接E'F'交BD于H点,过E作EG∥E'H交BD于G点,
易得四边形EE'HG为平行四边形.
∴EG=E'H,可得FH+EG的最小值为F'H+E'H的最小值,即E'F'为FH+EG的最小值.
作F'I⊥AC于I,
∵F是AB的中点,
∴F'是BC的中点,
∴△CIF'∽△COB,
∴,
∴OI=IC=OC=,F'I=2.
∵,∴AE'=×3=,
∴E'O=3-,∴E'I=E'O+OI=,
∵F'I=2,∴E'F'=,
故FH+EG的最小值为.
https://www.21cnjy.com/help/help_extract.php
2022年中考数学三轮复习(人教版)
提分微课 08
PA±PB型最值问题
●构图模型
●例题精析
●巩固训练
求解线段和(差)型最值问题,一般借助对称变换,通过化“折”为“直”,转化为“两点之间线段最短”或“垂线段最短”加以解决.
基本 图形 基本模型:在直线l上找一点P,PA+ PB最小 作点A关于直线l的对称点A',连接A'B,与直线l的交点即为点P 原理:两点之间线段最短
分别作点P关于OB,OA的对称点P',P″,连接P'P″,分别交OB,OA于点Q,R,此时PQ+PR+QR
(△PQR的周长)最小
(续表)
基本 图形 考虑到PQ为定值,故当QM +MN+NP最小时,PQ+MQ+MN +PN(四边形PQMN的周长)最小.类似地,当P',N,M,Q'共线时取最小值 在OA,OB上分别取点M,N,使得PM+
MN最小(垂线段最短)
此处M为“折点”,作点P关于OA的对称点P',则PM+MN=P'M+MN.过点P'作OB的垂线,与OA,OB的交点即为满足条件的M,N
原理:垂线段最短
(续表)
基本 图形 造桥选址问题:m∥n,则直线m,n上的点M,N,当MN⊥m,MN=AA', MN∥AA'且A',N,B三点共线时,AM +MN+BN的值最小(关键是将彼此分离的AM,BN通过平移连在一起)
PA-PB型最值问题:①当A,B两点在直线同侧时,连接AB并延长与直线的交点即为点P;②当A,B两点在直线异侧时,作点B关于直线的对称点B',则PA-PB=PA-PB'≤AB',故当A,
B',P共线时,PA-PB最大
(续表)
总结 求解此类问题的关键是构造对称.构图原则:同侧化异侧,折线变直线
例题精析
例 (1)如图W8-1①,正方形ABCD的边长为8,M在DC上,且DM=
2,N是AC上一动点,则DN+MN的最小值为 .
图W8-1
10
[解析]如图①,由条件易知,B,D关于直线AC对称,连接BM,则BM的长为DN+NM的最小值.
在直角三角形BCM中,BC=8,CM=8-2=6,
则BM==10.
例 (2)如图②,点A是半圆上(半径为1)的三等分点,B是的中点,P是直径MN上一动点,则PA+PB的最小值为 .
图W8-1
[解析]如图②,作B关于MN的对称点C,则C在圆上.连接AC,OC,则AC的长就是AP+BP的最小值.
∵∠AOC=∠AON+∠NOC=60°+30°=90°,
∴△AOC是等腰直角三角形,
∴AC=OA=,
即AP+BP的最小值是.
例 (3)如图③,在锐角三角形AB中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值为 .
图W8-1
4
[解析]如图③,作点N关于AD的对称点N',作BH⊥AC于H.
∵BM+MN=BM+MN',BM+MN'≥BH,
∴BH的长就是BM+MN的最小值.
∵∠BAC=45°,∴△ABH是等腰直角三角形,
∴BH=×4=4.
[思路分析]
求解时,首先分析求最值的线段中涉及几个动点、几个定点,再根据上面的类型转化求解.如(3)中,对于BM+MN,M,N是动点,B是定点,作点N关于直线AD的对称点N',则BM+MN=BM+
MN',所以当B,M,N'三点共线,即BN'⊥AC时,BM+MN取最小值.
巩固训练
1.如图W8-2,点P是边长为2的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边的中点,则MP+PN的最小值是 ( )
A.1 B.2 C.2 D.4
图W8-2
B
[解析]如图,作点M关于AC的对称点M',连接M'N交AC于P,此时MP+NP有最小值,最小值为M'N的长.
∵菱形ABCD关于AC对称,M是AB边的中点,
∴M'是AD的中点.
又∵N是BC边的中点,∴AM'∥BN,AM'=BN,
∴四边形ABNM'是平行四边形,∴M'N=AB=2,
即MP+NP的最小值为2.故选B.
2.如图W8-3,在等边三角形ABC中,AB=6,AD⊥BC,E是AC上的一点,M是AD上的一点,且AE=2,则ME+MC的最小值为 ( )
A. B.3 C.2 D.4
图W8-3
C
[解析]设点C关于直线AD的对称点是点B,连接BE,交AD于点M,
此时ME+MC的值最小.
过点B作BH⊥AC于点H,此时CH=AH=AC=3,
则EH=AH-AE=3-2=1,
BH==3.
在Rt△BHE中,BE==2,
即ME+MC的最小值为2.故选C.
3.如图W8-4,在Rt△AOB中,∠AOB=90°,OA=3,OB=4,以点O为圆心,2为半径的圆与OB交于点C,过点C作CD⊥OB交AB于点D,点P是边OA上的动点.当PC+PD最小时,OP的长为 ( )
A. B. C.1 D.
图W8-4
B
[解析]如图,延长CO交☉O于点E,连接ED,交AO于点P,此时PC+PD的值最小.
∵CD⊥OB,∴∠DCB=90°.
又∠AOB=90°,∴∠DCB=∠AOB,∴CD∥AO,∴.
∵OC=2,OB=4,∴BC=2,∴,解得CD=.
∵CD∥AO,∴,即,解得PO=.
故选B.
4.如图W8-5,在矩形ABCD中,AD=4,∠DAC=30°,点P,E分别在AC,AD上,则PE+PD的最小值是 .
图W8-5
2
[解析]如图,作点D关于直线AC的对称点D',当D',P,E三点共线,且D'E⊥AD时,PE+PD最小,易得CD=,
∠ADD'=60°,
DD'=4,所以D'E=2.
5.如图W8-6,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为 .
图W8-6
[解析]如图,作点P关于BD的对称点P',
则PK+QK=P'K+QK.当P',K,Q三点共线,且P'Q⊥CD时,
PK+QK取得最小值.
过点A作AE⊥CD于点E.
∵在菱形ABCD中,AB=AD=2,∠BAD=120°,
∴∠ADC=60°,∴AE=AD·sin∠ADC=2×,
∵P'Q⊥CD,AE⊥CD,AB∥CD,∴P'Q=AE=.
∴PK+QK的最小值为.
6.如图W8-7,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=S矩形ABCD,则点P到A,B两点的距离之和PA+PB的最小值为 .
图W8-7
4
[解析]如图,设△PAB中AB边上的高是h,
∵S△PAB=S矩形ABCD,∴AB·h=AB·AD,
∴h=AD=2,∴动点P在与AB平行且与
AB的距离是2的线段l(线段l的长度为4,且点P不过线段l与AD,BC的交点)上,如图,作点A关于直线l的对称点A',连接AA',BA',交l于P',则BA'即为所求的最短距离.
在Rt△ABA'中,AB=4,AA'=2+2=4,
∴BA'==4,即PA+PB的最小值为4.
7.如图W8-8,正比例函数y=x的图象与反比例函数y=在第一象限的图象交于A点,点B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,点P为x轴上一点,当PA+PB的值最小时,点P的
坐标为 .
图W8-8
(,0)
[解析]联立得解得∴A(2,1).
设A点关于x轴的对称点为C,
则C点的坐标为(2,-1).
连接BC交x轴于点P,此时PA+PB的值最小,如图所示.
设直线BC的解析式为y=mx+n.
易知B点坐标为(1,2),
将B和C的坐标代入得解得
∴BC的解析式为y=-3x+5.
当y=0时,x=,∴P点坐标为(,0).
8.如图W8-9,抛物线y=x2+2x-3与x轴交于A,B两点,与y轴交于点C,点P是抛物线对称轴上任意一点,若点D,E,F分别是BC,BP,
PC的中点,连接DE,DF,则DE+DF的最小值为 .
图W8-9
[解析]因为点D,E,F分别是BC,BP,PC的中点,所以DE,DF是△PBC的中位线,所以DE=PC,DF=PB,所以DE+DF=(PC+PB),故本题可转化为求PC+PB的最小值,因为B,C为定点,P为对称轴上一动点,点A,B关于对称轴对称,所以连接AC,PC+PB的最小值等于AC的长度,由抛物线解析式可得A(-3,0),C(0,-3),
∴AC=3,DE+DF的最小值=AC=.
9.如图W8-10,四边形ABCD中,∠C=50°,∠B=∠D=90°,E,F分别是BC,DC上的动点,当△AEF的周长最小时,∠EAF的度数为
.
图W8-10
80°
[解析]如图,分别作A关于BC和CD的对称点A',A″,连接A'A″,交BC于E,交CD于F,则A'A″的长即为△AEF周长的最小值.作DA延长线AH,易知∠DAB=130°,∠HAA'=50°.
又∠EA'A=∠EAA',∠FAD=∠A″,
且∠EA'A+∠EAA'=∠AEF,∠FAD+∠A″=∠AFE,
所以∠AEF+∠AFE=∠EA'A+∠EAA'+∠FAD+∠A″
=2(∠AA'E+∠A″)=2∠HAA'=100°,
所以∠EAF=180°-100°=80°.
10.[2019·陕西]如图W8-11,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6.P为对角线BD上一点,则PM-PN的最大值为 .
图W8-11
2
[解析]作点M关于BD的对称点M',根据对称性可知M'在AB上且AM'=2,连接PM',则PM'=PM,∴PM-PN=PM'-PN≤M'N,
当M',N,P共线时,此时PM'-PN=M'N,取得最大值.
∵,∴△AM'N∽△ABC,
即△AM'N是等腰直角三角形,
∴M'N=AM'=2,
∴PM-PN的最大值为2.
11.如图W8-12,已知直线l1∥l2,l1,l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ=4,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ最小,此时PA+BQ= .
图W8-12
16
[解析]作PE⊥l1于E,交l2于F,在PF上截取PC=8,连接QC交l2于B,此时PA+AB+BQ最短.作QD⊥PF交PF的延长线于D.
在Rt△PQD中,∵∠D=90°,PQ=4,PD=18,
∴DQ=,CD=PD-PC=18-8=10.
∵AB=PC=8,AB∥PC,
∴四边形ABCP是平行四边形,∴PA=BC,
∴PA+BQ=CB+BQ=QC==16.
故答案为16.
12.如图W8-13,已知菱形ABCD的对角线AC,BD相交于点O,
AC=6,BD=8,点E在AD上,,点F为AB的中点,点G,H为BD上的动点,GH=1,连接FH,EG,则FH+EG的最小值为 .
图W8-13
[解析]∵四边形ABCD是菱形,∴AC⊥BD,
∴∠AOD=90°,OB=OD,OC=OA,
∵AC=6,BD=8,∴OA=3,OB=4,
作F关于DB的对称点F',作EE'⊥OA于E',
∴EE'∥OD,∴△AE'E∽△AOD,
∴,∴EE'=1,
连接E'F'交BD于H点,过E作EG∥E'H交BD于G点,
易得四边形EE'HG为平行四边形.
∴EG=E'H,可得FH+EG的最小值为F'H+E'H的最小值,即E'F'为FH+EG的最小值.
作F'I⊥AC于I,
∵F是AB的中点,
∴F'是BC的中点,
∴△CIF'∽△COB,
∴,
∴OI=IC=OC=,F'I=2.
∵,∴AE'=×3=,
∴E'O=3-,∴E'I=E'O+OI=,
∵F'I=2,∴E'F'=,
故FH+EG的最小值为.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
