2022中考数学三轮冲刺考前提分微课09 PA+kPB型最值问题 课件(共31张PPT)
文档属性
| 名称 | 2022中考数学三轮冲刺考前提分微课09 PA+kPB型最值问题 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 11:03:51 | ||
图片预览






文档简介
(共31张PPT)
2022年中考数学三轮复习(人教版)
考前提分微课 09
PA+kPB型最值问题
●构图模型
●例题精析
●巩固训练
“PA+kPB”型的最值问题是近几年中考考查的热点更是难点.当k值为1时,即可转化为“PA+PB”之和最短问题,就可用我们常见的“将军饮马”模型来处理,即可以转化为轴对称问题来处理.当k取任意不为1的正数时,若再以常规的轴对称思想来解决问题,则无法进行,因此必须转换思路.其中动点P在直线上运动的类型称为“胡不归”问题.
构图模型
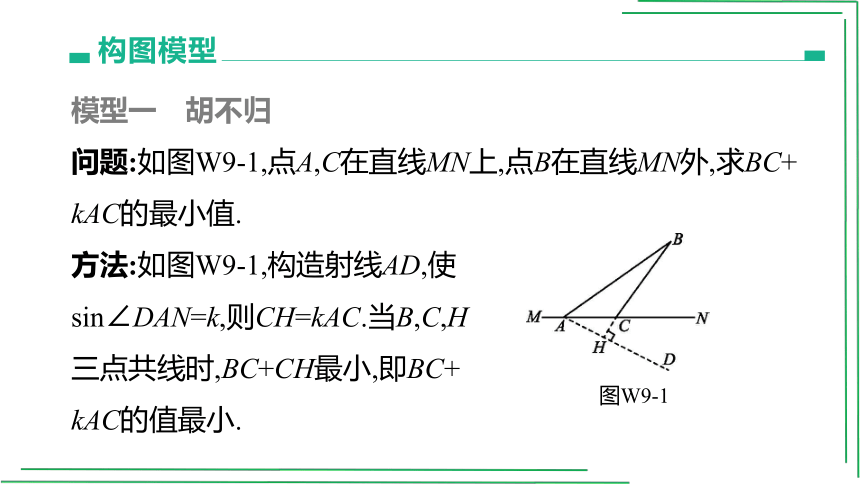
模型一 胡不归
问题:如图W9-1,点A,C在直线MN上,点B在直线MN外,求BC+
kAC的最小值.
方法:如图W9-1,构造射线AD,使
sin∠DAN=k,则CH=kAC.当B,C,H
三点共线时,BC+CH最小,即BC+
kAC的值最小.
图W9-1
模型二 阿氏圆
阿氏圆:已知平面上两点A,B,则所有满足PA=k·PB(k≠1)的点P的轨迹是一个圆,这个轨迹最早由古希腊数学家阿波罗尼斯发现,故称“阿氏圆”.
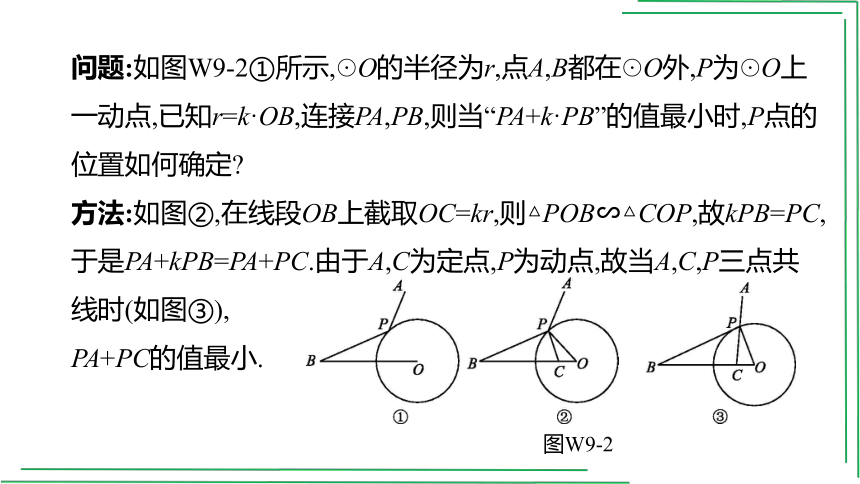
问题:如图W9-2①所示,☉O的半径为r,点A,B都在☉O外,P为☉O上一动点,已知r=k·OB,连接PA,PB,则当“PA+k·PB”的值最小时,P点的位置如何确定
方法:如图②,在线段OB上截取OC=kr,则△POB∽△COP,故kPB=PC,于是PA+kPB=PA+PC.由于A,C为定点,P为动点,故当A,C,P三点共线时(如图③),
PA+PC的值最小.
图W9-2
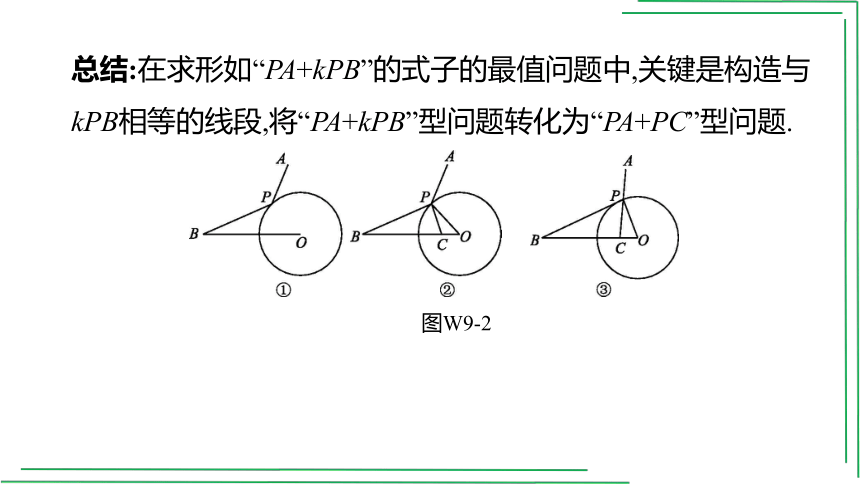
总结:在求形如“PA+kPB”的式子的最值问题中,关键是构造与kPB相等的线段,将“PA+kPB”型问题转化为“PA+PC”型问题.
图W9-2
例题精析
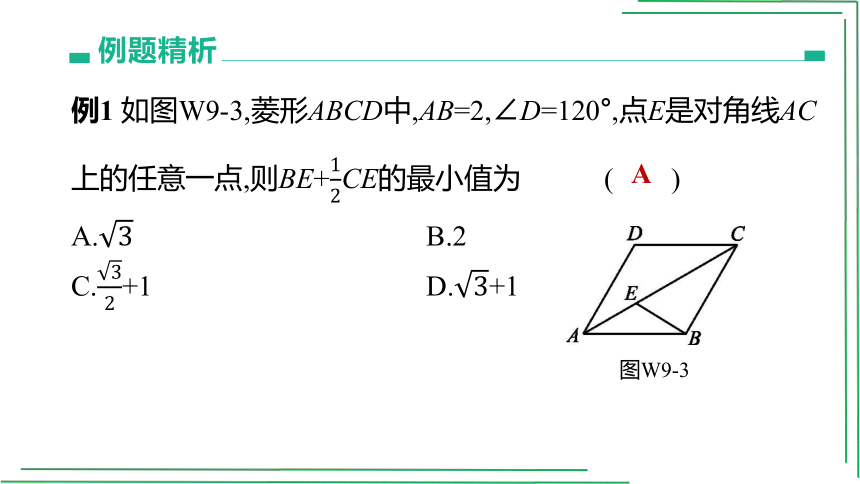
例1 如图W9-3,菱形ABCD中,AB=2,∠D=120°,点E是对角线AC上的任意一点,则BE+CE的最小值为 ( )
A. B.2
C.+1 D.+1
图W9-3
A
思路分析:
菱形ABCD中,由∠D=120°得∠DCE=30°,过点E作EF
⊥CD,则EF=CE
当B,E,F三点共线时,
BE+CE最小,为菱形的高
[解析]如图所示,过点E作EF⊥DC,垂足为F,
∵DA=DC,∠D=120°,∴∠ACD=30°,
∴在Rt△EFC中,EF=EC,
∴BE+CE=BE+EF,易知当B,E,F三点共线时,BE+EF最小,
∴BE+CE的最小值=BF=BC=×2=.
故选A.
例2 如图W9-4,四边形ABCD为边长为4的正方形,☉B的半径为2,P为☉B上一动点,则PD+PC的最小值为 ( )
A.6 B.5 C.4 D.2
图W9-4
B
思路分析:
在BC上取一点E,使BE=1,则△BPE∽△BCP,PE=PC
当D,P,E三点共线时,
PD+PC的值最小
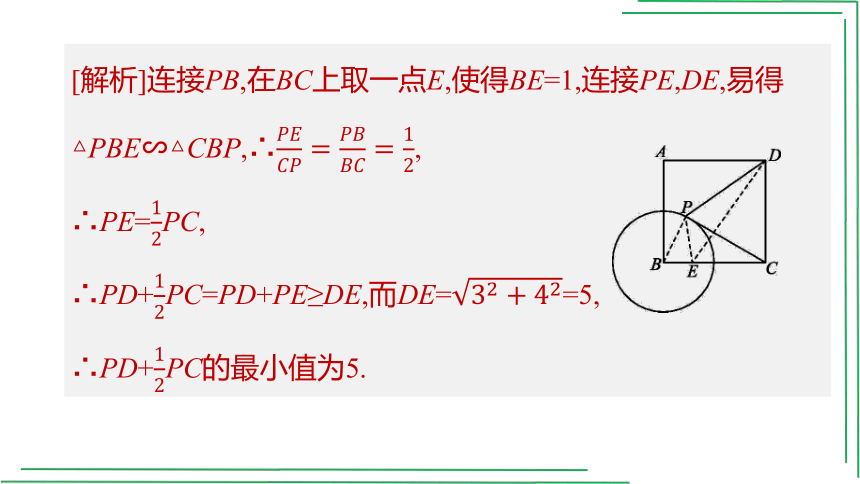
[解析]连接PB,在BC上取一点E,使得BE=1,连接PE,DE,易得△PBE∽△CBP,∴,
∴PE=PC,
∴PD+PC=PD+PE≥DE,而DE==5,
∴PD+PC的最小值为5.
巩固训练
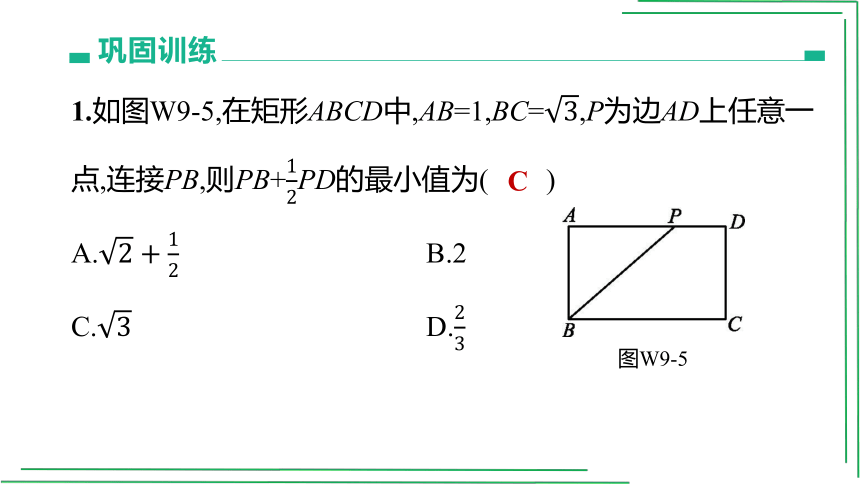
1.如图W9-5,在矩形ABCD中,AB=1,BC=,P为边AD上任意一点,连接PB,则PB+PD的最小值为( )
A. B.2
C. D.
图W9-5
C
[解析]连接BD,易得∠ADB=30°,过点P作PF⊥BD,垂足为F,则PF=PD,作点B关于AD的对称点B',过点B'作B'G⊥BD,当点G与点F重合时,PB+PD的值最小,此时PB+PD=B'G=.
2.如图W9-6,在正方形ABCD中,AB=8,点P是正方形ABCD内部的一点,且满足BP=4,则PD+PC的最小值为 ( )
A.6 B.8 C.10 D.12
图W9-6
C
[解析]如图,在BC边上取一点E,使BE=2,连接PE,DE,
则△PBE∽△CBP,则PE=PC,PD+PE≥DE(当D,P,E三点共线时,等号成立),
故PD+PC的最小值为
=10.
3.[2020·芜湖一模]如图W9-7,△ABC中,AB=AC=10,tanA=2,
BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是( )
A.2 B.4
C.5 D.10
图W9-7
B
[解析]方法一:如图,作DH⊥AB于H,CM⊥AB于M.
∵BE⊥AC,∴∠AEB=90°,∵tanA==2,
∴设AE=a,BE=2a,则有100=a2+4a2,∴a2=20,
∴a=2或-2(舍去),
即AE=2,BE=2a=4,
∵AB=AC,BE⊥AC,CM⊥AB,
∴CM=BE=4.
在Rt△BHD和Rt△BAE中,∠BHD=∠BEA=90°,
∴sin∠DBH=,
∴DH=BD,∴CD+BD=CD+DH,
由图可得CD+DH≥CM,∴CD+BD≥4,
∴CD+BD的最小值为4.
方法二:作CM⊥AB于M,交BE于点D,则点D满足题意.通过三角形相似或三角函数证得BD=DM,
从而得到CD+BD=CM=4.
故选B.
4.如图W9-8,在△ABC中,∠ACB=90°,BC=12,AC=9,以点C为圆心,6为半径的圆上有一个动点D,连接AD,BD,CD,则AD+BD最小值为( )
A.3 B.4
C.5 D.6
图W9-8
B
[解析]在CA上截取CM,使CM=4,连接BM,DM,
易得△DCM∽△ACD,所以,即DM=AD,
因为DM+BD≥BM,所以AD+BD≥BM.在Rt△CBM中,由勾股定理得BM==4,
所以当点M,D,B在同一直线上时,
AD+BD取得最小值,最小值为4.
5.如图W9-9,在Rt△ABC中,∠B=90°,AB=CB=2,以点B为圆心作圆B与AC相切,P为圆B上一动点,则PA+PC的最小值为 .
图W9-9
[解析]在BC上截取BE=1,连接EP,BP.
易得☉B半径为 ,故BP=
,∠EBP=∠PBC,
∴△EBP∽△PBC.∴,EP=PC.
∴PA+PC=PA+EP≥AE=.当A,E,P三点共线即EA与☉B交于点P时取等号.故PA+PC的最小值为.
6.如图W9-10,点A,B在☉O上,OA=OB=6,且OA⊥OB,点C是OA的中点,点D在OB上,OD=4,动点P在☉O上,则2PC+PD的最小值为 .
图W9-10
4
[解析]如图,连接OP,在射线OA上截取AE=6,连接DE,交☉O于点P,此时2PC+PD最小.
∴,又∠POC=∠EOP,
∴△OPC∽△OEP,∴,∴PE=2PC.
∴2PC+PD=PE+PD=DE.
在Rt△OED中,DE==4,即2PC+PD的最小值为4.
7.如图W9-11,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(-1,0),B(0,-),C(2,0),其中对称轴与x轴交于点D.
(1)抛物线的顶点坐标为 .
(2)若P为y轴上的一个动点,连接PD,
求PB+PD的最小值.
图W9-11
(,-)
(1)[解析]由题意得解得
∴抛物线的解析式为y=x2-x-,
∵y=x2-x-(x-)2-,
∴顶点坐标为(,-).
(2)若P为y轴上的一个动点,连接PD,
求PB+PD的最小值.
图W9-11
解:(2)如图,连接AB,作DH⊥AB于H,交OB于P,
此时PB+PD最小.
理由:∵OA=1,OB=,
∴tan∠ABO=,
∴∠ABO=30°,∴PH=PB,
∴PB+PD=PH+PD=DH,
∴此时PB+PD最短(垂线段最短).
在Rt△ADH中,∵∠AHD=90°,AD=,∠HAD=60°,
∴sin60°=,∴DH=,
∴PB+PD的最小值为.
https://www.21cnjy.com/help/help_extract.php
2022年中考数学三轮复习(人教版)
考前提分微课 09
PA+kPB型最值问题
●构图模型
●例题精析
●巩固训练
“PA+kPB”型的最值问题是近几年中考考查的热点更是难点.当k值为1时,即可转化为“PA+PB”之和最短问题,就可用我们常见的“将军饮马”模型来处理,即可以转化为轴对称问题来处理.当k取任意不为1的正数时,若再以常规的轴对称思想来解决问题,则无法进行,因此必须转换思路.其中动点P在直线上运动的类型称为“胡不归”问题.
构图模型
模型一 胡不归
问题:如图W9-1,点A,C在直线MN上,点B在直线MN外,求BC+
kAC的最小值.
方法:如图W9-1,构造射线AD,使
sin∠DAN=k,则CH=kAC.当B,C,H
三点共线时,BC+CH最小,即BC+
kAC的值最小.
图W9-1
模型二 阿氏圆
阿氏圆:已知平面上两点A,B,则所有满足PA=k·PB(k≠1)的点P的轨迹是一个圆,这个轨迹最早由古希腊数学家阿波罗尼斯发现,故称“阿氏圆”.
问题:如图W9-2①所示,☉O的半径为r,点A,B都在☉O外,P为☉O上一动点,已知r=k·OB,连接PA,PB,则当“PA+k·PB”的值最小时,P点的位置如何确定
方法:如图②,在线段OB上截取OC=kr,则△POB∽△COP,故kPB=PC,于是PA+kPB=PA+PC.由于A,C为定点,P为动点,故当A,C,P三点共线时(如图③),
PA+PC的值最小.
图W9-2
总结:在求形如“PA+kPB”的式子的最值问题中,关键是构造与kPB相等的线段,将“PA+kPB”型问题转化为“PA+PC”型问题.
图W9-2
例题精析
例1 如图W9-3,菱形ABCD中,AB=2,∠D=120°,点E是对角线AC上的任意一点,则BE+CE的最小值为 ( )
A. B.2
C.+1 D.+1
图W9-3
A
思路分析:
菱形ABCD中,由∠D=120°得∠DCE=30°,过点E作EF
⊥CD,则EF=CE
当B,E,F三点共线时,
BE+CE最小,为菱形的高
[解析]如图所示,过点E作EF⊥DC,垂足为F,
∵DA=DC,∠D=120°,∴∠ACD=30°,
∴在Rt△EFC中,EF=EC,
∴BE+CE=BE+EF,易知当B,E,F三点共线时,BE+EF最小,
∴BE+CE的最小值=BF=BC=×2=.
故选A.
例2 如图W9-4,四边形ABCD为边长为4的正方形,☉B的半径为2,P为☉B上一动点,则PD+PC的最小值为 ( )
A.6 B.5 C.4 D.2
图W9-4
B
思路分析:
在BC上取一点E,使BE=1,则△BPE∽△BCP,PE=PC
当D,P,E三点共线时,
PD+PC的值最小
[解析]连接PB,在BC上取一点E,使得BE=1,连接PE,DE,易得△PBE∽△CBP,∴,
∴PE=PC,
∴PD+PC=PD+PE≥DE,而DE==5,
∴PD+PC的最小值为5.
巩固训练
1.如图W9-5,在矩形ABCD中,AB=1,BC=,P为边AD上任意一点,连接PB,则PB+PD的最小值为( )
A. B.2
C. D.
图W9-5
C
[解析]连接BD,易得∠ADB=30°,过点P作PF⊥BD,垂足为F,则PF=PD,作点B关于AD的对称点B',过点B'作B'G⊥BD,当点G与点F重合时,PB+PD的值最小,此时PB+PD=B'G=.
2.如图W9-6,在正方形ABCD中,AB=8,点P是正方形ABCD内部的一点,且满足BP=4,则PD+PC的最小值为 ( )
A.6 B.8 C.10 D.12
图W9-6
C
[解析]如图,在BC边上取一点E,使BE=2,连接PE,DE,
则△PBE∽△CBP,则PE=PC,PD+PE≥DE(当D,P,E三点共线时,等号成立),
故PD+PC的最小值为
=10.
3.[2020·芜湖一模]如图W9-7,△ABC中,AB=AC=10,tanA=2,
BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是( )
A.2 B.4
C.5 D.10
图W9-7
B
[解析]方法一:如图,作DH⊥AB于H,CM⊥AB于M.
∵BE⊥AC,∴∠AEB=90°,∵tanA==2,
∴设AE=a,BE=2a,则有100=a2+4a2,∴a2=20,
∴a=2或-2(舍去),
即AE=2,BE=2a=4,
∵AB=AC,BE⊥AC,CM⊥AB,
∴CM=BE=4.
在Rt△BHD和Rt△BAE中,∠BHD=∠BEA=90°,
∴sin∠DBH=,
∴DH=BD,∴CD+BD=CD+DH,
由图可得CD+DH≥CM,∴CD+BD≥4,
∴CD+BD的最小值为4.
方法二:作CM⊥AB于M,交BE于点D,则点D满足题意.通过三角形相似或三角函数证得BD=DM,
从而得到CD+BD=CM=4.
故选B.
4.如图W9-8,在△ABC中,∠ACB=90°,BC=12,AC=9,以点C为圆心,6为半径的圆上有一个动点D,连接AD,BD,CD,则AD+BD最小值为( )
A.3 B.4
C.5 D.6
图W9-8
B
[解析]在CA上截取CM,使CM=4,连接BM,DM,
易得△DCM∽△ACD,所以,即DM=AD,
因为DM+BD≥BM,所以AD+BD≥BM.在Rt△CBM中,由勾股定理得BM==4,
所以当点M,D,B在同一直线上时,
AD+BD取得最小值,最小值为4.
5.如图W9-9,在Rt△ABC中,∠B=90°,AB=CB=2,以点B为圆心作圆B与AC相切,P为圆B上一动点,则PA+PC的最小值为 .
图W9-9
[解析]在BC上截取BE=1,连接EP,BP.
易得☉B半径为 ,故BP=
,∠EBP=∠PBC,
∴△EBP∽△PBC.∴,EP=PC.
∴PA+PC=PA+EP≥AE=.当A,E,P三点共线即EA与☉B交于点P时取等号.故PA+PC的最小值为.
6.如图W9-10,点A,B在☉O上,OA=OB=6,且OA⊥OB,点C是OA的中点,点D在OB上,OD=4,动点P在☉O上,则2PC+PD的最小值为 .
图W9-10
4
[解析]如图,连接OP,在射线OA上截取AE=6,连接DE,交☉O于点P,此时2PC+PD最小.
∴,又∠POC=∠EOP,
∴△OPC∽△OEP,∴,∴PE=2PC.
∴2PC+PD=PE+PD=DE.
在Rt△OED中,DE==4,即2PC+PD的最小值为4.
7.如图W9-11,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(-1,0),B(0,-),C(2,0),其中对称轴与x轴交于点D.
(1)抛物线的顶点坐标为 .
(2)若P为y轴上的一个动点,连接PD,
求PB+PD的最小值.
图W9-11
(,-)
(1)[解析]由题意得解得
∴抛物线的解析式为y=x2-x-,
∵y=x2-x-(x-)2-,
∴顶点坐标为(,-).
(2)若P为y轴上的一个动点,连接PD,
求PB+PD的最小值.
图W9-11
解:(2)如图,连接AB,作DH⊥AB于H,交OB于P,
此时PB+PD最小.
理由:∵OA=1,OB=,
∴tan∠ABO=,
∴∠ABO=30°,∴PH=PB,
∴PB+PD=PH+PD=DH,
∴此时PB+PD最短(垂线段最短).
在Rt△ADH中,∵∠AHD=90°,AD=,∠HAD=60°,
∴sin60°=,∴DH=,
∴PB+PD的最小值为.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
