6.2.3向量的数乘运算 课件(共30张PPT)
文档属性
| 名称 | 6.2.3向量的数乘运算 课件(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 12:46:23 | ||
图片预览











文档简介
(共30张PPT)
6.2.3 向量的数乘运算
问题:一只兔子向东一秒钟的位移对应的向量为 ,
那么它在同一方向上按照相同的速度行走3秒钟的位
移对应的向量怎样表示?是 吗?兔子在相反方向
上按照相同的速度行走3秒钟的位移对应的向量又怎
样表示?是 吗 请同学们自己思考.
1.通过实例分析,掌握平面向量数乘运算及运算法则,理解其几何意义.
2.了解平面向量的线性运算性质及其几何意义.
3.理解两个向量共线的含义.
1.运用向量的数乘运算培养学生的数学运算能力,数乘向量可以判断几何中三点共线和两直线平行等问题,培养学生的逻辑推理能力。
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
向量数乘的定义
思考1:已知非零向量 ,如何求作向量 + + 和(- )+(- )+ (- )?
提示:
O
A
B
C
N
M
O
P
(- )+(- )+(- )
思考2:向量 + + 和(- )+(- )+(- )分别如何简化其表示形式?
提示:
+ + 记为3 ,
(- )+(- )+(- )记为-3 .
思考3:向量3 和-3 与向量 的大小和方向有什么关系?
O
A
B
C
O
M
N
P
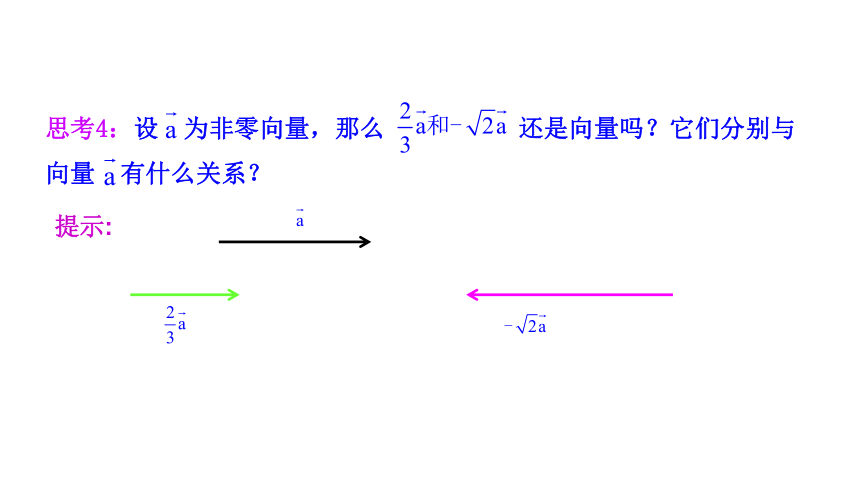
思考4:设 为非零向量,那么 还是向量吗?它们分别与
向量 有什么关系?
提示:
思考5:一般地,我们规定实数λ与向量 的积是一个向量,这种运算
叫做向量的数乘.记作λ ,该向量的长度及方向与向量 有什么关系?
提示:
(1)|λ |=|λ|| |;
(2)λ>0时,λ 与 方向相同;
λ<0时,λ 与 方向相反;
λ=0时,λ = .
【即时训练】
C
向量数乘的运算律及共线向量基本定理
思考1:你认为-2×(5 ),2 +2 ,
可分别转化为什么运算?
提示:
-2× (5 )= -10 ;
2 + 2 = 2( + );
(3+ ) =3 +
思考2:一般地,设λ,μ为实数,则λ(μ ),
(λ+μ) ,λ( + )分别等于什么?
=
提示:
B
C
A
D
E
提升总结:向量数乘的运算律
思考3:对于向量 ( )和 ,若存在实数λ,
使 ,则向量 与 的方向有什么关系?
提示:共线
思考4:若向量 ( )与 共线,则一定存在实
数λ,使 成立吗?
提示:一定存在
思考5:综上可得向量共线定理:向量 ( )与
共线,当且仅当有唯一一个实数λ,使 =λ .
若 = ,上述定理成立吗?
提示:不成立
【即时训练】
B
例1.计算
(1)(-3)×4 ;
(2)3( + )-2( - )- ;
(3)(2 +3 - )-(3 -2 + ).
【解析】
向量与实数之间可以像多项式一样进行运算.
【变式练习】
例2.如图,□ABCD的两条对角线相交于点M,且 = ,
= ,你能用 , 表示 , 吗?
M
A B
D C
【变式练习】
如图,在平行四边形ABCD中,点M是AB的中点,点N在线段BD上,且
有BN= BD,求证:M,N,C三点共线.
提示:设 ,
则
所以M,N,C三点共线.
例3.如图,已知任意两个非零向量 试作
你能判断A,B,C三点之间的
位置关系吗?为什么?
O
A
B
C
分析:
A,B,C三点共线.
【解析】分别作向量 ,过点A,C作直线AC.观察发现,不论向量 怎样变化,点B始终在直线AC
上,猜想A,B,C三点共线.
事实上,因为
1. 向量数乘
的定义.
2.向量数乘的运算律.
3.共线向量定
理.
1.向量的数乘运算可类似于代数多项式运算.
2.用图形中的已知向量表示所求向量,应结合已知和所求,将所求向量反复分解,直到全部可以用已知向量表
示即可.
数学抽象:
向量数乘概念
逻辑推理:
向量共线的充要条件及其应用
数学运算:
向量的线性运算
向量的数乘运算中,“同类项”“公因式”指向量,实数看作是向量的系数
D
A
B
-2
黎明的曙光对暗夜是彻底的决裂,对彩霞是伟大的奠基。
停止前进的脚步,江河就会沦为一潭死水。
6.2.3 向量的数乘运算
问题:一只兔子向东一秒钟的位移对应的向量为 ,
那么它在同一方向上按照相同的速度行走3秒钟的位
移对应的向量怎样表示?是 吗?兔子在相反方向
上按照相同的速度行走3秒钟的位移对应的向量又怎
样表示?是 吗 请同学们自己思考.
1.通过实例分析,掌握平面向量数乘运算及运算法则,理解其几何意义.
2.了解平面向量的线性运算性质及其几何意义.
3.理解两个向量共线的含义.
1.运用向量的数乘运算培养学生的数学运算能力,数乘向量可以判断几何中三点共线和两直线平行等问题,培养学生的逻辑推理能力。
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
向量数乘的定义
思考1:已知非零向量 ,如何求作向量 + + 和(- )+(- )+ (- )?
提示:
O
A
B
C
N
M
O
P
(- )+(- )+(- )
思考2:向量 + + 和(- )+(- )+(- )分别如何简化其表示形式?
提示:
+ + 记为3 ,
(- )+(- )+(- )记为-3 .
思考3:向量3 和-3 与向量 的大小和方向有什么关系?
O
A
B
C
O
M
N
P
思考4:设 为非零向量,那么 还是向量吗?它们分别与
向量 有什么关系?
提示:
思考5:一般地,我们规定实数λ与向量 的积是一个向量,这种运算
叫做向量的数乘.记作λ ,该向量的长度及方向与向量 有什么关系?
提示:
(1)|λ |=|λ|| |;
(2)λ>0时,λ 与 方向相同;
λ<0时,λ 与 方向相反;
λ=0时,λ = .
【即时训练】
C
向量数乘的运算律及共线向量基本定理
思考1:你认为-2×(5 ),2 +2 ,
可分别转化为什么运算?
提示:
-2× (5 )= -10 ;
2 + 2 = 2( + );
(3+ ) =3 +
思考2:一般地,设λ,μ为实数,则λ(μ ),
(λ+μ) ,λ( + )分别等于什么?
=
提示:
B
C
A
D
E
提升总结:向量数乘的运算律
思考3:对于向量 ( )和 ,若存在实数λ,
使 ,则向量 与 的方向有什么关系?
提示:共线
思考4:若向量 ( )与 共线,则一定存在实
数λ,使 成立吗?
提示:一定存在
思考5:综上可得向量共线定理:向量 ( )与
共线,当且仅当有唯一一个实数λ,使 =λ .
若 = ,上述定理成立吗?
提示:不成立
【即时训练】
B
例1.计算
(1)(-3)×4 ;
(2)3( + )-2( - )- ;
(3)(2 +3 - )-(3 -2 + ).
【解析】
向量与实数之间可以像多项式一样进行运算.
【变式练习】
例2.如图,□ABCD的两条对角线相交于点M,且 = ,
= ,你能用 , 表示 , 吗?
M
A B
D C
【变式练习】
如图,在平行四边形ABCD中,点M是AB的中点,点N在线段BD上,且
有BN= BD,求证:M,N,C三点共线.
提示:设 ,
则
所以M,N,C三点共线.
例3.如图,已知任意两个非零向量 试作
你能判断A,B,C三点之间的
位置关系吗?为什么?
O
A
B
C
分析:
A,B,C三点共线.
【解析】分别作向量 ,过点A,C作直线AC.观察发现,不论向量 怎样变化,点B始终在直线AC
上,猜想A,B,C三点共线.
事实上,因为
1. 向量数乘
的定义.
2.向量数乘的运算律.
3.共线向量定
理.
1.向量的数乘运算可类似于代数多项式运算.
2.用图形中的已知向量表示所求向量,应结合已知和所求,将所求向量反复分解,直到全部可以用已知向量表
示即可.
数学抽象:
向量数乘概念
逻辑推理:
向量共线的充要条件及其应用
数学运算:
向量的线性运算
向量的数乘运算中,“同类项”“公因式”指向量,实数看作是向量的系数
D
A
B
-2
黎明的曙光对暗夜是彻底的决裂,对彩霞是伟大的奠基。
停止前进的脚步,江河就会沦为一潭死水。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
