【中考数学总复习】第13课时 二次函数的图象与性质 课件
文档属性
| 名称 | 【中考数学总复习】第13课时 二次函数的图象与性质 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 14:50:29 | ||
图片预览








文档简介
(共29张PPT)
第三单元 函 数
第13课时 二次函数的图象与性质
(每年第10题必考,3分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:九下第二章P28-P63;
人教:九上第二十二章P27-P57.
二次函数表
达式的确定
二次函数
图象的平移
二次函数与
一元二次方程、
不等式的关系
二次函数的概念
与一元二次
方程的关系
与不等式的关系
二次函数的
图象与性质
二次函数
的图象与性质
根据二次函数解析
式判断函数性质
根据二次函数解析
式判断函数图象
根据二次函数图象
判断相关结论
二次函数的概念
考点
1
形如y=ax2+bx+c(a,b,c为常数,a≠0)的函数叫做二次函数.其中a、b、c分别是函数解析式的二次项系数、一次项系数和常数项.
返回思维导图
二次函数的图象与性质
考点
2
1. 根据二次函数解析式判断函数性质
函数 二次函数y=ax2+bx+c(a≠0)
对称轴 (1)直接利用公式x=________
(2)配方转化为顶点式y=a(x-h)2+k,则对称轴为________
注:还可利用x= (其中x1、x2为y值相等的两点的横坐标)求解
顶点坐标 (1)直接利用顶点坐标公式_________________
(2)配方化为顶点式y=a(x-h)2+k,则顶点坐标为________
(3)将对称轴x=x0代入函数表达式求得对应的y0
x=h
(h,k)
返回思维导图
函数 二次函数y=ax2+bx+c(a≠0) 增减性 a>0 对称轴左侧,即x< , y随x的增大而________
对称轴右侧,即x> , y随x的增大而________
a<0 对称轴左侧,即x< , y随x的增大而________
对称轴右侧,即x> , y随x的增大而________
最大值或最小值 a>0 当x=________时,y最小值=
a<0
当x=________时,y最大值=
减小
增大
增大
减小
返回思维导图
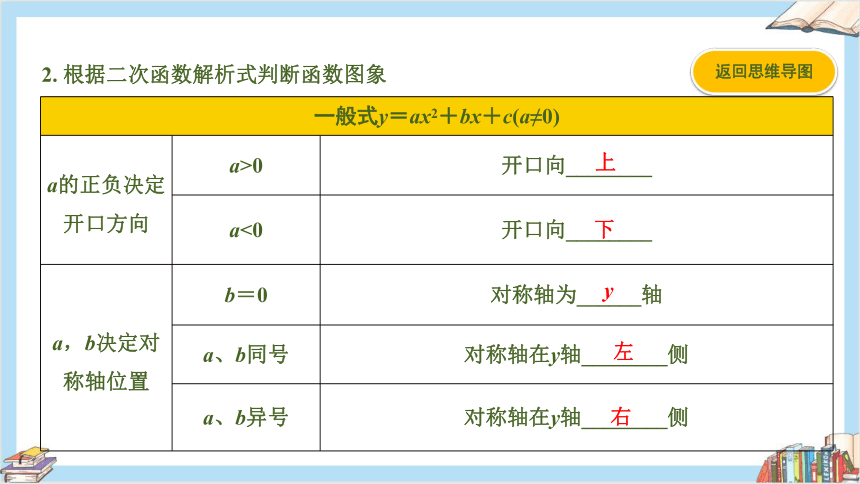
2. 根据二次函数解析式判断函数图象
一般式y=ax2+bx+c(a≠0) a的正负决定开口方向 a>0 开口向________
a<0 开口向________
a,b决定对称轴位置 b=0 对称轴为______轴
a、b同号 对称轴在y轴________侧
a、b异号 对称轴在y轴________侧
上
下
y
左
右
返回思维导图
一般式y=ax2+bx+c(a≠0) c决定与y轴交点位置 c=0 抛物线过原点
c>0 抛物线与y轴交于________半轴
c<0 抛物线与y轴交于________半轴
b2-4ac决定与x轴交点个数 b2-4ac=0 与x轴有唯一的交点(顶点)
b2-4ac>0 与x轴有________交点
b2-4ac<0 与x轴没有交点
正
负
两个
返回思维导图
3. 根据二次函数图象判断相关结论
图象
结论 a________0 b________0 c________0 b2-4ac________0 a________0 b________0 c________0 b2-4ac________0 a________0 b________0 c________0 b2-4ac________0 a________0
b________0
c________0
b2-4ac________0
>
>
<
>
<
=
>
>
>
>
>
<
<
<
>
=
返回思维导图
图象
结论 a________0 b________0 c________0 b2-4ac________0 a________0 b________0 c________0 b2-4ac________0 a________0 b________0 c________0 b2-4ac________0 a________0
b________0
c________0
b2-4ac________0
>
>
>
<
>
>
>
=
<
>
>
=
>
=
=
=
返回思维导图
二次函数表达式的确定
考点
3
表达式的三种形式
1. 一般式:y=ax2+bx+c(a≠0,a、b、c为常数);
2. 顶点式:y=a(x-h)2+k(a≠0,a,h,k为常数),其中(h,k)是抛物线的顶点坐标;
3. 交点式:y=a(x-x1)(x-x2)(a≠0,a为常数,x1,x2为抛物线与x轴的两个交点的横坐标).
返回思维导图
二次函数图象的平移
考点
4
平移前的解析式 平移方向 平移后的解析式 简记
y=a(x-h)2+k 向左平移m个单位 y=a(x-h )2+k 左“+”
向右平移m个单位 y=a(x-h )2+k 右“-”
向上平移m个单位 y=a(x-h)2+k 上“+”
向下平移m个单位 y=a(x-h)2+k 下“-”
返回思维导图
【提分要点】(1)在一般式y=ax2+bx+c(a≠0)或顶点式y=a(x-h)2+k(a≠0)中,左右平移给x加减平移单位,上下平移给等号右边整体加减平移单位.
(2)二次函数图象平移的实质是图象上点的整体平移(研究顶点坐标为主),平移过程中a不变,因此可先求出其顶点坐标,根据顶点坐标的平移求解即可.
返回思维导图
二次函数与一元二次方程、不等式的关系
考点
5
1. 二次函数与一元二次方程的关系
方程ax2+bx+c=0的解是二次函数y=ax2+bx+c与x轴交点的横坐标值
抛物线与x轴有两个交点 方程有两个______的实数根 b2-4ac>0
抛物线与x轴有一个交点 方程有两个相等的实数根 b2-4ac______0
抛物线与x轴无交点 方程__________ b2-4ac______0
不相等
=
无实数根
<
返回思维导图
2. 二次函数与不等式的关系
(1)ax2+bx+c>0的解集 函数y=ax2+bx+c的图象位于x轴________对应的点的横坐标的取值范围;
(2)ax2+bx+c<0的解集 函数y=ax2+bx+c的图象位于x轴________对应的点的横坐标的取值范围.
上方
下方
返回思维导图
典例“串”考点
例1 已知抛物线y=x2-2bx+b2-1.
(1)抛物线开口向______,化为顶点式为 ;
(2)抛物线的对称轴为直线____________;
(3)抛物线的顶点坐标为____________;
(4)该二次函数有最________值(填“大”或“小”),为____________;
(5)抛物线与y轴的交点坐标为____________,与x轴的交点坐标为
;
(6)若抛物线对称轴在直线x=1右侧,则抛物线不经过第______象限;
(7)若点(b-3,y1)、(b+3,y2)都在抛物线上,则y1与y2的大小关系为__________;
上
y=(x-b)2-1
x=b
(b,-1)
小
-1
(0,b2-1)
(b+1,0)或(b-1,0)
三
y1=y2
(8)当-1<b<1,若x=2b,则y____0(填“>”、“<”或“=”);
(9)若b=2.
①在如图所示的平面直角坐标系中画出函数图象;
②若y随x的增大而增大,则x的取值范围为________;
③当-2≤x≤5时,y的最大值为__________,最小值为________.
例1题图
<
x≥2
15
-1
例1题解图
(9)①画出函数图像如解图:
例2 在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示.
例2题图
判断下列结论的正误:
(1)abc<0 ( )
(2)4ac-b2<0 ( )
(3)2a+b=0 ( )
(4)3a+b<0 ( )
√
√
×
×
(5)3a+c<0( )
(6)二次函数的最小值为a-b+c( )
(7)9a-3b+c=0( )
(8)当y<0时,-3<x<1( )
(9)对于任意实数m,a-b≥m(am+b)总成立( )
(10)若该函数与y轴的交点在(0,-1)和(0,-2)之间(包括端点),则 ≤a≤ ( )
(11)方程ax2+bx+c-3=0的两根一个小于1,另一个大于-3 ( )
√
√
√
√
×
×
×
例3 已知抛物线y=-x2+3x+4.
(1)将抛物线向左平移2个单位长度,再向上平移1个单位长度,平移后的抛物线表达式为______________
(2)将抛物线平移后,得到的新的抛物线的顶点为( , ),则平移方式为 ;
(3)抛物线关于原点对称的抛物线表达式为 ,关于x轴对称的抛物线的表达式为 ,关于y轴对称的抛物线的表达式为 ;
(4)抛物线关于直线x=1对称的抛物线的表达式为 ;
(5)抛物线关于直线y=-2对称的抛物线的表达式为 ;
y=-x2-x+7
向下平移6个单位长度
y=x2+3x-4
y=x2-3x-4
y=-x2-3x+4
y=-x2+x+6
y=x2-3x-8
【提分要点】抛物线y=a(x-h)2+k(a≠0)的平移、轴对称、旋转变换可以对应看作其顶点(h,k)的平移、轴对称、旋转变换,掌握各种变化后的a值和顶点(h′,k′)便可轻松得到变换后的二次函数表达式,具体如下:
y=a(x-h)2+k a 顶点(h,k)
平移变换 不变 变
轴对称变换 x轴 相反数 (h,-k)
y轴 不变 (-h,k)
旋转变换 绕顶点(180°) 相反数 (h,k)
绕原点(180°) 相反数 (-h,-k)
陕西5年真题、副题“明”考法
命题点
1
二次函数的图象与性质(必考)
类型一 函数增减性
1. (2018陕西副题10题3分)已知抛物线y=x2+(m+1)x+m,当x=1时,y>0,且当x<-2时,y的值随x值的增大而减小,则m的取值范围是( )
A.m>-1 B.m<3
C.-1C
类型二 与函数图象的对称轴或顶点有关的问题(5年4考)
2. (2018陕西10题3分)对于抛物线y=ax2+(2a-1)x+a-3,当x=1时,y>0,则这条抛物线的顶点一定在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
3. (2019陕西10题3分)在同一平面直角坐标系中,若抛物线y=x2+(2m-1)x+2m-4与y=x2-(3m+n)x+n关于y轴对称,则符合条件的m、n的值为( )
A. m= ,n= B. m=5,n=-6
C. m=-1,n=6 D. m=1,n=-2
C
D
4. (2015陕西副题10题3分)在平面直角坐标系中,有两条抛物线关于x轴对称,且它们的顶点相距10个单位长度.若其中一条抛物线的函数表达式为y=x2+6x+m,则m的值是( )
A. -4或-14 B. -4或14 C. 4或-14 D. 4或14
5. (2017陕西10题3分)已知抛物线y=x2-2mx-4(m>0)的顶点M关于坐标原点O的对称点为M′.若点M′ 在这条抛物线上,则点M的坐标为( )
A. (1,-5) B. (3,-13) C. (2,-8) D. (4,-20)
6. (2017陕西副题10题3分)已知抛物线y=x2+bx+c的对称轴为x=1,且它与x轴交于A、B两点.若AB的长是6,则该抛物线的顶点坐标为( )
A. (1,9) B. (1,8) C. (1,-9) D. (1,-8)
D
C
C
7. (2016陕西10题3分)已知抛物线y=-x2-2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
A. B. C. D. 2
D
类型三 函数图象与坐标轴的交点问题(2015.10)
8. (2015陕西10题3分)下列关于二次函数y=ax2-2ax+1(a>1)的图象与x轴交点的判断,正确的是( )
A. 没有交点
B. 只有一个交点,且它位于y轴右侧
C. 有两个交点,且它们均位于y轴左侧
D. 有两个交点,且它们均位于y轴右侧
D
命题点
2
二次函数图象的平移
9. (2019陕西副题10题3分)在平面直角坐标系中,将抛物线y=x2-(a-2)x+a2-1向右平移4个单位长度,平移后的抛物线与y轴的交点为A(0,3),则平移后的抛物线的对称轴为( )
A. x=-1 B. x=1 C. x=-2 D. x=2
10. (2016陕西副题10题3分)将抛物线M:y= x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M′.若抛物线M′与x轴交于A、B两点,M′的顶点记为C,则∠ACB=( )
A. 45° B. 60° C. 90° D. 120°
D
C
点击链接至练习册
第三单元 函 数
第13课时 二次函数的图象与性质
(每年第10题必考,3分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:九下第二章P28-P63;
人教:九上第二十二章P27-P57.
二次函数表
达式的确定
二次函数
图象的平移
二次函数与
一元二次方程、
不等式的关系
二次函数的概念
与一元二次
方程的关系
与不等式的关系
二次函数的
图象与性质
二次函数
的图象与性质
根据二次函数解析
式判断函数性质
根据二次函数解析
式判断函数图象
根据二次函数图象
判断相关结论
二次函数的概念
考点
1
形如y=ax2+bx+c(a,b,c为常数,a≠0)的函数叫做二次函数.其中a、b、c分别是函数解析式的二次项系数、一次项系数和常数项.
返回思维导图
二次函数的图象与性质
考点
2
1. 根据二次函数解析式判断函数性质
函数 二次函数y=ax2+bx+c(a≠0)
对称轴 (1)直接利用公式x=________
(2)配方转化为顶点式y=a(x-h)2+k,则对称轴为________
注:还可利用x= (其中x1、x2为y值相等的两点的横坐标)求解
顶点坐标 (1)直接利用顶点坐标公式_________________
(2)配方化为顶点式y=a(x-h)2+k,则顶点坐标为________
(3)将对称轴x=x0代入函数表达式求得对应的y0
x=h
(h,k)
返回思维导图
函数 二次函数y=ax2+bx+c(a≠0) 增减性 a>0 对称轴左侧,即x< , y随x的增大而________
对称轴右侧,即x> , y随x的增大而________
a<0 对称轴左侧,即x< , y随x的增大而________
对称轴右侧,即x> , y随x的增大而________
最大值或最小值 a>0 当x=________时,y最小值=
a<0
当x=________时,y最大值=
减小
增大
增大
减小
返回思维导图
2. 根据二次函数解析式判断函数图象
一般式y=ax2+bx+c(a≠0) a的正负决定开口方向 a>0 开口向________
a<0 开口向________
a,b决定对称轴位置 b=0 对称轴为______轴
a、b同号 对称轴在y轴________侧
a、b异号 对称轴在y轴________侧
上
下
y
左
右
返回思维导图
一般式y=ax2+bx+c(a≠0) c决定与y轴交点位置 c=0 抛物线过原点
c>0 抛物线与y轴交于________半轴
c<0 抛物线与y轴交于________半轴
b2-4ac决定与x轴交点个数 b2-4ac=0 与x轴有唯一的交点(顶点)
b2-4ac>0 与x轴有________交点
b2-4ac<0 与x轴没有交点
正
负
两个
返回思维导图
3. 根据二次函数图象判断相关结论
图象
结论 a________0 b________0 c________0 b2-4ac________0 a________0 b________0 c________0 b2-4ac________0 a________0 b________0 c________0 b2-4ac________0 a________0
b________0
c________0
b2-4ac________0
>
>
<
>
<
=
>
>
>
>
>
<
<
<
>
=
返回思维导图
图象
结论 a________0 b________0 c________0 b2-4ac________0 a________0 b________0 c________0 b2-4ac________0 a________0 b________0 c________0 b2-4ac________0 a________0
b________0
c________0
b2-4ac________0
>
>
>
<
>
>
>
=
<
>
>
=
>
=
=
=
返回思维导图
二次函数表达式的确定
考点
3
表达式的三种形式
1. 一般式:y=ax2+bx+c(a≠0,a、b、c为常数);
2. 顶点式:y=a(x-h)2+k(a≠0,a,h,k为常数),其中(h,k)是抛物线的顶点坐标;
3. 交点式:y=a(x-x1)(x-x2)(a≠0,a为常数,x1,x2为抛物线与x轴的两个交点的横坐标).
返回思维导图
二次函数图象的平移
考点
4
平移前的解析式 平移方向 平移后的解析式 简记
y=a(x-h)2+k 向左平移m个单位 y=a(x-h )2+k 左“+”
向右平移m个单位 y=a(x-h )2+k 右“-”
向上平移m个单位 y=a(x-h)2+k 上“+”
向下平移m个单位 y=a(x-h)2+k 下“-”
返回思维导图
【提分要点】(1)在一般式y=ax2+bx+c(a≠0)或顶点式y=a(x-h)2+k(a≠0)中,左右平移给x加减平移单位,上下平移给等号右边整体加减平移单位.
(2)二次函数图象平移的实质是图象上点的整体平移(研究顶点坐标为主),平移过程中a不变,因此可先求出其顶点坐标,根据顶点坐标的平移求解即可.
返回思维导图
二次函数与一元二次方程、不等式的关系
考点
5
1. 二次函数与一元二次方程的关系
方程ax2+bx+c=0的解是二次函数y=ax2+bx+c与x轴交点的横坐标值
抛物线与x轴有两个交点 方程有两个______的实数根 b2-4ac>0
抛物线与x轴有一个交点 方程有两个相等的实数根 b2-4ac______0
抛物线与x轴无交点 方程__________ b2-4ac______0
不相等
=
无实数根
<
返回思维导图
2. 二次函数与不等式的关系
(1)ax2+bx+c>0的解集 函数y=ax2+bx+c的图象位于x轴________对应的点的横坐标的取值范围;
(2)ax2+bx+c<0的解集 函数y=ax2+bx+c的图象位于x轴________对应的点的横坐标的取值范围.
上方
下方
返回思维导图
典例“串”考点
例1 已知抛物线y=x2-2bx+b2-1.
(1)抛物线开口向______,化为顶点式为 ;
(2)抛物线的对称轴为直线____________;
(3)抛物线的顶点坐标为____________;
(4)该二次函数有最________值(填“大”或“小”),为____________;
(5)抛物线与y轴的交点坐标为____________,与x轴的交点坐标为
;
(6)若抛物线对称轴在直线x=1右侧,则抛物线不经过第______象限;
(7)若点(b-3,y1)、(b+3,y2)都在抛物线上,则y1与y2的大小关系为__________;
上
y=(x-b)2-1
x=b
(b,-1)
小
-1
(0,b2-1)
(b+1,0)或(b-1,0)
三
y1=y2
(8)当-1<b<1,若x=2b,则y____0(填“>”、“<”或“=”);
(9)若b=2.
①在如图所示的平面直角坐标系中画出函数图象;
②若y随x的增大而增大,则x的取值范围为________;
③当-2≤x≤5时,y的最大值为__________,最小值为________.
例1题图
<
x≥2
15
-1
例1题解图
(9)①画出函数图像如解图:
例2 在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示.
例2题图
判断下列结论的正误:
(1)abc<0 ( )
(2)4ac-b2<0 ( )
(3)2a+b=0 ( )
(4)3a+b<0 ( )
√
√
×
×
(5)3a+c<0( )
(6)二次函数的最小值为a-b+c( )
(7)9a-3b+c=0( )
(8)当y<0时,-3<x<1( )
(9)对于任意实数m,a-b≥m(am+b)总成立( )
(10)若该函数与y轴的交点在(0,-1)和(0,-2)之间(包括端点),则 ≤a≤ ( )
(11)方程ax2+bx+c-3=0的两根一个小于1,另一个大于-3 ( )
√
√
√
√
×
×
×
例3 已知抛物线y=-x2+3x+4.
(1)将抛物线向左平移2个单位长度,再向上平移1个单位长度,平移后的抛物线表达式为______________
(2)将抛物线平移后,得到的新的抛物线的顶点为( , ),则平移方式为 ;
(3)抛物线关于原点对称的抛物线表达式为 ,关于x轴对称的抛物线的表达式为 ,关于y轴对称的抛物线的表达式为 ;
(4)抛物线关于直线x=1对称的抛物线的表达式为 ;
(5)抛物线关于直线y=-2对称的抛物线的表达式为 ;
y=-x2-x+7
向下平移6个单位长度
y=x2+3x-4
y=x2-3x-4
y=-x2-3x+4
y=-x2+x+6
y=x2-3x-8
【提分要点】抛物线y=a(x-h)2+k(a≠0)的平移、轴对称、旋转变换可以对应看作其顶点(h,k)的平移、轴对称、旋转变换,掌握各种变化后的a值和顶点(h′,k′)便可轻松得到变换后的二次函数表达式,具体如下:
y=a(x-h)2+k a 顶点(h,k)
平移变换 不变 变
轴对称变换 x轴 相反数 (h,-k)
y轴 不变 (-h,k)
旋转变换 绕顶点(180°) 相反数 (h,k)
绕原点(180°) 相反数 (-h,-k)
陕西5年真题、副题“明”考法
命题点
1
二次函数的图象与性质(必考)
类型一 函数增减性
1. (2018陕西副题10题3分)已知抛物线y=x2+(m+1)x+m,当x=1时,y>0,且当x<-2时,y的值随x值的增大而减小,则m的取值范围是( )
A.m>-1 B.m<3
C.-1
类型二 与函数图象的对称轴或顶点有关的问题(5年4考)
2. (2018陕西10题3分)对于抛物线y=ax2+(2a-1)x+a-3,当x=1时,y>0,则这条抛物线的顶点一定在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
3. (2019陕西10题3分)在同一平面直角坐标系中,若抛物线y=x2+(2m-1)x+2m-4与y=x2-(3m+n)x+n关于y轴对称,则符合条件的m、n的值为( )
A. m= ,n= B. m=5,n=-6
C. m=-1,n=6 D. m=1,n=-2
C
D
4. (2015陕西副题10题3分)在平面直角坐标系中,有两条抛物线关于x轴对称,且它们的顶点相距10个单位长度.若其中一条抛物线的函数表达式为y=x2+6x+m,则m的值是( )
A. -4或-14 B. -4或14 C. 4或-14 D. 4或14
5. (2017陕西10题3分)已知抛物线y=x2-2mx-4(m>0)的顶点M关于坐标原点O的对称点为M′.若点M′ 在这条抛物线上,则点M的坐标为( )
A. (1,-5) B. (3,-13) C. (2,-8) D. (4,-20)
6. (2017陕西副题10题3分)已知抛物线y=x2+bx+c的对称轴为x=1,且它与x轴交于A、B两点.若AB的长是6,则该抛物线的顶点坐标为( )
A. (1,9) B. (1,8) C. (1,-9) D. (1,-8)
D
C
C
7. (2016陕西10题3分)已知抛物线y=-x2-2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
A. B. C. D. 2
D
类型三 函数图象与坐标轴的交点问题(2015.10)
8. (2015陕西10题3分)下列关于二次函数y=ax2-2ax+1(a>1)的图象与x轴交点的判断,正确的是( )
A. 没有交点
B. 只有一个交点,且它位于y轴右侧
C. 有两个交点,且它们均位于y轴左侧
D. 有两个交点,且它们均位于y轴右侧
D
命题点
2
二次函数图象的平移
9. (2019陕西副题10题3分)在平面直角坐标系中,将抛物线y=x2-(a-2)x+a2-1向右平移4个单位长度,平移后的抛物线与y轴的交点为A(0,3),则平移后的抛物线的对称轴为( )
A. x=-1 B. x=1 C. x=-2 D. x=2
10. (2016陕西副题10题3分)将抛物线M:y= x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M′.若抛物线M′与x轴交于A、B两点,M′的顶点记为C,则∠ACB=( )
A. 45° B. 60° C. 90° D. 120°
D
C
点击链接至练习册
同课章节目录
