【中考数学总复习】第20课时 相似三角形的实际应用 课件
文档属性
| 名称 | 【中考数学总复习】第20课时 相似三角形的实际应用 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 14:50:29 | ||
图片预览







文档简介
(共31张PPT)
第四单元 三角形
第20课时 相似三角形的实际应用
(5年4考,7分)
目
录
典例“串”考点
1
2
陕西5年真题、副题“明”考法
典例“串”考点
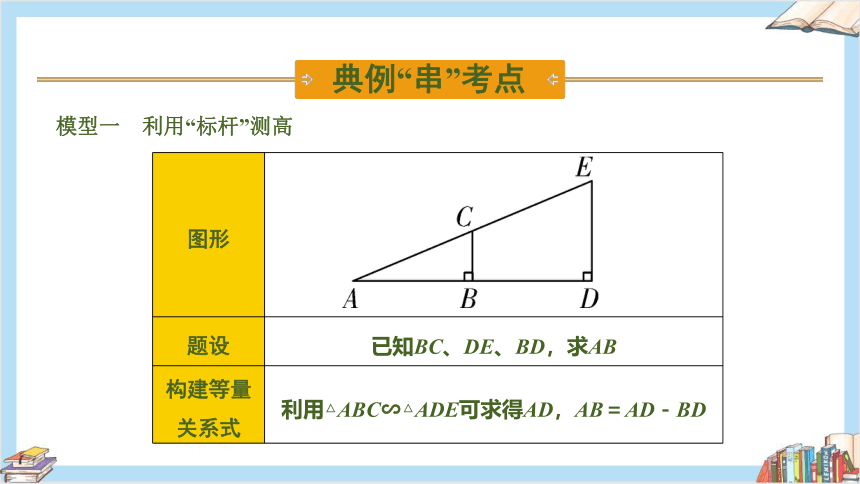
模型一 利用“标杆”测高
图形
题设 已知BC、DE、BD,求AB
构建等量关系式 利用△ABC∽△ADE可求得AD,AB=AD-BD
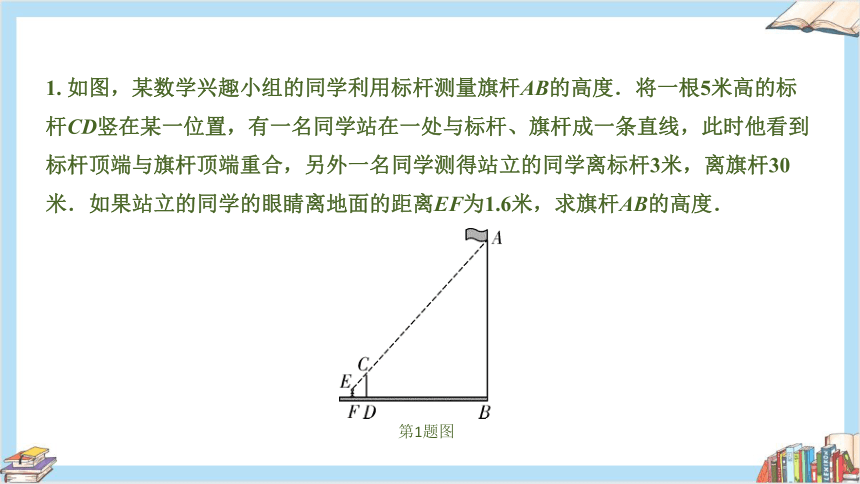
1. 如图,某数学兴趣小组的同学利用标杆测量旗杆AB的高度.将一根5米高的标杆CD竖在某一位置,有一名同学站在一处与标杆、旗杆成一条直线,此时他看到标杆顶端与旗杆顶端重合,另外一名同学测得站立的同学离标杆3米,离旗杆30米.如果站立的同学的眼睛离地面的距离EF为1.6米,求旗杆AB的高度.
第1题图
解:如解图,过点E作EH⊥AB于点H,交CD于点G.
由题意可得四边形EFDG、GDHB都是矩形,AB∥CD∥EF.
∴△ECG∽△EAH,
由题意可得EG=FD=3,GH=BD=30,
CG=CD-GD=CD-EF=5-1.6=3.4,
∴AH=34米,∴AB=AH+HB=34+1.6=35.6米.
答:旗杆AB的高为35.6米.
第1题解图
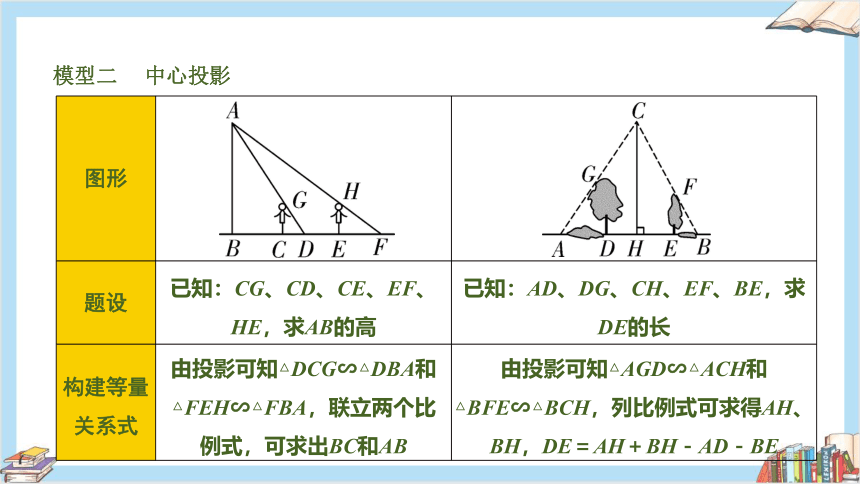
模型二 中心投影
图形
题设 已知:CG、CD、CE、EF、HE,求AB的高 已知:AD、DG、CH、EF、BE,求DE的长
构建等量关系式 由投影可知△DCG∽△DBA和△FEH∽△FBA,联立两个比例式,可求出BC和AB 由投影可知△AGD∽△ACH和△BFE∽△BCH,列比例式可求得AH、BH,DE=AH+BH-AD-BE
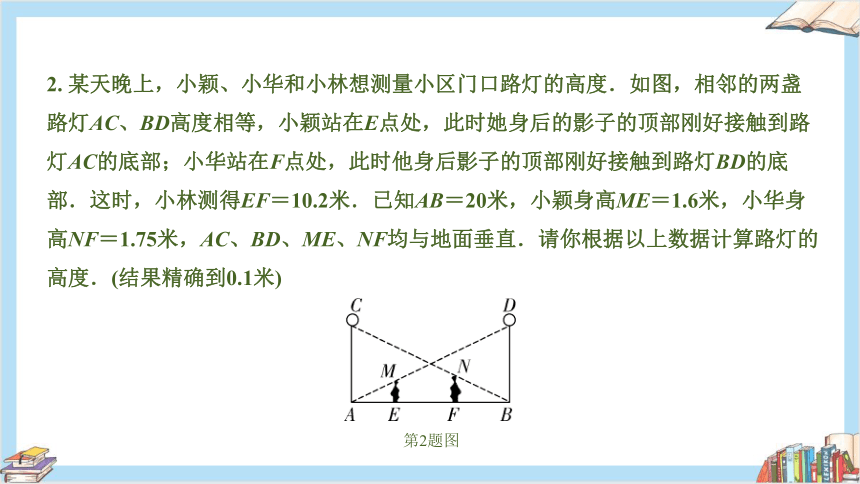
2. 某天晚上,小颖、小华和小林想测量小区门口路灯的高度.如图,相邻的两盏路灯AC、BD高度相等,小颖站在E点处,此时她身后的影子的顶部刚好接触到路灯AC的底部;小华站在F点处,此时他身后影子的顶部刚好接触到路灯BD的底部.这时,小林测得EF=10.2米.已知AB=20米,小颖身高ME=1.6米,小华身高NF=1.75米,AC、BD、ME、NF均与地面垂直.请你根据以上数据计算路灯的高度.(结果精确到0.1米)
第2题图
解:设AE=x,则BF=20-10.2-x=9.8-x,
∵ME∥BD,
∴△AME∽△ADB,
∵NF∥AC, ∴△BNF∽△BCA,
∴BD≈6.8,
答:路灯的高度约为6.8米.
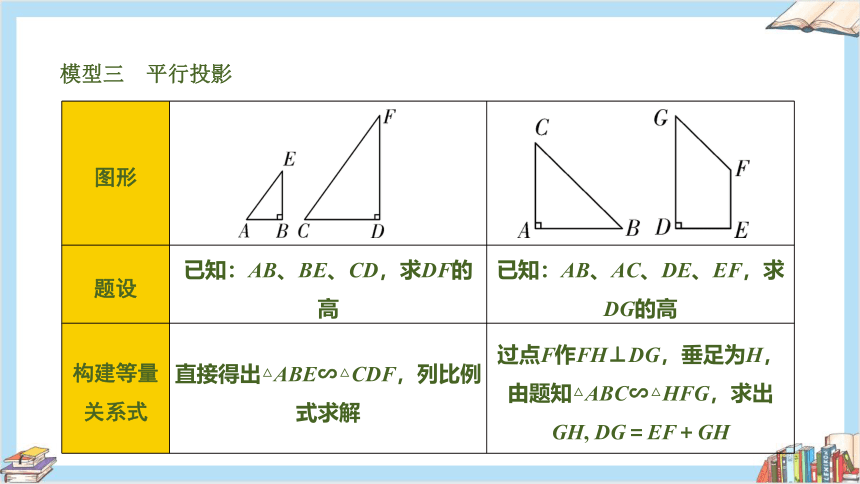
模型三 平行投影
图形
题设 已知:AB、BE、CD,求DF的高 已知:AB、AC、DE、EF,求DG的高
构建等量关系式 直接得出△ABE∽△CDF,列比例式求解 过点F作FH⊥DG,垂足为H,由题知△ABC∽△HFG,求出GH, DG=EF+GH
3. 如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.请你根据以上测量数据,求电线杆AB的高度.
第3题图
解:如解图,过点C作CG⊥AB于点G,则四边形CDBG为矩形,
∴GC=BD=3米,GB=CD=2米.∵∠NMF=∠AGC=90°,NF∥AC,
∴∠NFM=∠ACG,
∴△NMF∽△AGC,
∴AB=AG+GB=6+2=8米,
答:电线杆AB的高为8米.
第3题解图
模型四 镜面反射、投影
图形
题设 已知∠α、AB、AO、OC,求CD的高 已知AB在水中的倒影为BD,及EF、EC、CB,求AB
构建等量关系式 直接得出△ABO∽△CDO,列比例式求解 直接得出△FEC∽△DBC,列比例式求解
4. 小雁塔位于唐长安城安仁坊荐福寺内,又称“荐福寺塔”,是西安的标志性建筑之一.在一次社会实践中,小梅和小鹏想通过测量小雁塔的高度,来检验自己掌握知识和运用知识的能力.如图,由于无法直接到塔的底部,小梅在D处利用测角仪测得塔顶A的仰角为25°,同时小鹏在C、B之间的地面上放置一平面镜(平面镜厚度不计),当小鹏移动平面镜至E处时,小梅恰好通过平面镜看到了塔顶A.经测量,DC=1.5米,CE=3米.已知DC⊥CB,AB⊥CB,且C、E、B在同一条直线上,不考虑其它因素,请你根据题中提供的相关信息,计算小雁塔的高AB.(结果精确到0.1米,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47).
第4题图
解:如解图,过点D作DF⊥AB于点F,则四边形BCDF是矩形,
∴BC=DF,BF=CD=1.5米,
∵∠DEC=∠AEB,∠DCE=∠ABE=90°,∴△DCE∽△ABE,
设AB=x,则BE=2x,∴AF=x-1.5,DF=BC=3+2x,
在Rt△AFD中,tan25°=
解得x≈48.5,即AB≈48.5米,
答:小雁塔的高AB约为48.5米.
第4题解图
模型五 固定视角
图形
题设 已知AB、BC、BE,求BD
构建等量关系式 由一对直角和一锐角相等构造相似三角形,即△ABD∽△CBE,再列比例关系式求解
5. 如图,小明想通过自己所学的知识测量一段笔直的高架桥MN上DQ段的运行距离,设计了如下的测量方案:已知在高架桥的一侧有一排居民楼AB(楼顶AB与高架桥MN在同一水平面上,且AB与点D正好在同一直线上),测得AB=35米,小明先站在A处,测得视线与高架桥MN的垂直距离AH=15米,小明又站在B处,使得视线与BQ在一条直线上,此时测得BQ=45米,且∠QBA=90°,求此高架桥上DQ段的运行距离.
第5题图
解:根据题意得∠AHD=∠QBA=90°,∠ADH=∠QDB,
∴△ADH∽△QDB,
∵AH=15米,BQ=45米,AB=35米,
在Rt△AHD中,根据勾股定理得AD2=AH2+DH2,∴(3DH-35)2=152+DH2,
解得AD=3DH-35.
解得DH=20或DH=6.25(舍去),
答:此高架桥上DQ段的运行距离为75米.
解得DQ=75(米).
陕西5年真题、副题“明”考法
相似三角形的实际应用(5年4考)
命题点
1. (2018陕西20题7分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽,测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C、A共线.已知:CB⊥AD,ED⊥AD,测得BC=1 m,DE=1.5 m,BD=8.5 m,测量示意图
如图所示.请根据相关测量信息,求河宽AB.
第1题图
解:∵CB⊥AD,ED⊥AD,
∴CB∥ED.
又∵∠CAB=∠EAD,∴△ABC∽△ADE,(3分)
∵BC=1 m,DE=1.5 m,BD=8.5 m,AD=AB+BD,
∴AB=17 m,
答:河宽AB为17 m. (7分)
2. (2015陕西20题7分)晚饭后,小聪和小军在社区广场散步.小聪问小军:“你有多高?”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,
AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高
BE的长.(结果精确到0.01米)
第2题图
解:由题意得∠CAD=∠MND=90°,∠CDA=∠MDN,
∴△CAD∽△MND,
∴MN=9.6.(3分)
又∵∠EBF=∠MNF=90°,∠EFB=∠MFN,
∴△EBF∽△MNF,(5分)
解得BE≈1.75.(6分)
答:小军的身高BE约为1.75米.(7分)
3. (2015陕西副题20题7分)周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳篷的宽度.如图,由于无法直接测量,小凯便在楼前地面上选择了一条直线EF,通过在直线EF上选点观测,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳篷A点处;当他位于N′点时,视线从M′点通过D点正好落在遮阳篷B点处.这样观测到的两个点A、B间的距离即为遮阳篷的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、MN、M′N′均垂直于EF,
MN=M′N′,露台的宽CD=GE.测得GE=5米,
EN=12.3米,NN′=6.2米.请你根据以上信息,求出
遮阳篷的宽AB是多少米?(结果精确到0.01米)
第3题图
解:如解图,延长MM′交DE于点P,
∵AG、DE、MN、M′N′均垂直于EF,MN=M′N′,
∴四边形M′MNN′和四边形PMNE均为矩形,
∴MM′=NN′=6.2,PM=EN=12.3.(2分)
∵AB∥CD∥PM,∴△ACD∽△DPM,
△ABD∽△MM′D,
解得AB≈2.52.
答:遮阳篷的宽AB约为2.52米.(7分)
第3题解图
4. (2016陕西20题7分)某市为了打造森林城市,树立城市新地标,实现绿色、共享发展理念,在城南建起了“望月阁”及环阁公园.小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度,来检验自己掌握知识和运用知识的能力.他们经过观察发现,观测点与“望月阁”底部间的距离不易测得,因此经过研究需要两次测量.于是他们首先用平面镜进行测量,方法如下:如图,小芳在小亮和“望月阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C.镜子不动,小亮看着镜面上的标记,他来回走动,走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合.这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米;
然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:如图,小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.
如图,已知:AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计.请你根据题中提供的相关信息,求出“望月阁”的高AB的长度.
第4题图
解:由题意得∠ABC=∠EDC=∠GFH=90°,∠ACB=∠ECD,∠AFB=∠GHF. ∴△ABC∽△EDC,
△ABF∽△GFH,(3分)
解得AB=99米.
答:“望月阁”的高AB为99米.(7分)
5. (2019陕西20题7分)小明想利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学们带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是,他们先在古树周围的空地上选择了一点D,并在点D处安装了测倾器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5 m,并在点G处的地面上水平放置了一个小平面镜,小明沿BG方向移动,当移动到点F时,他刚好在小平
面镜内看到这棵古树的顶端A的像,此时,测得FG=2 m,
小明眼睛与地面的距离EF=1.6 m,测倾器的高CD =0.5 m.
已知点F、G、D、B在同一水平直线上,且EF、CD、AB均
垂直于FB,求这棵古树的高AB.(小平面镜的大小忽略不计)
第5题图
解:如解图,过点C作CH⊥AB于点H,则CH=BD,BH=CD=0.5.(1分)
在Rt△ACH中,∠ACH=45°,∴AH=CH=BD.
∴AB=AH+BH=BD+0.5.(2分)
∵EF⊥FB,AB⊥FB,∴∠EFG=∠ABG=90°.
由题意,易知∠EGF=∠AGB,
∴△EFG∽△ABG.(4分)
解得BD=17.5 m.(6分)
∴AB=17.5+0.5=18(m).
答:这棵古树的高AB为18 m.(7分)
第5题解图
6. (2019陕西副题20题7分)新学期,小华和小明被选为升旗手,为了更好地完成升旗任务,他俩想利用测倾器和阳光下的影子来测量学校旗杆的高度PA.如图所示,旗杆直立于旗台上的点P处,他们的测量方法是:首先,在阳光下,小华站在旗杆影子的顶端F处,此时,量得小华的影长FG=2 m,小华身高EF=1.6 m;然后,在旗杆影子上的点D处,安装测倾器CD,测得旗杆顶端A的仰角为49°,量得CD=0.6 m,DF=6 m,旗台高BP=1.2 m.已知在测量过程中,点B、D、F、G在同一水平直线上,点A、P、B在同一条直线上,
AB、CD、EF均垂直于BG.求旗杆的高度PA.
(参考数据:sin49°≈0.8,cos49°≈0.7,tan49°≈1.2)
第6题图
解:如解图,过点C作CH⊥AB于点H,则CH=BD,BH=CD=0.6.
在Rt△AHC中,tan49°=
∴AH=1.2BD.
∴AB=AH+HB=1.2BD+0.6.(3分)
连接AF、EG.由题意,可得△EFG∽△ABF.
解得BD=10.5,∴AB=13.2.(6分) ∴PA=AB-PB=13.2-1.2=12(m).
答:旗杆的高度PA约为12 m.(7分)
第6题解图
点击链接至练习册
第四单元 三角形
第20课时 相似三角形的实际应用
(5年4考,7分)
目
录
典例“串”考点
1
2
陕西5年真题、副题“明”考法
典例“串”考点
模型一 利用“标杆”测高
图形
题设 已知BC、DE、BD,求AB
构建等量关系式 利用△ABC∽△ADE可求得AD,AB=AD-BD
1. 如图,某数学兴趣小组的同学利用标杆测量旗杆AB的高度.将一根5米高的标杆CD竖在某一位置,有一名同学站在一处与标杆、旗杆成一条直线,此时他看到标杆顶端与旗杆顶端重合,另外一名同学测得站立的同学离标杆3米,离旗杆30米.如果站立的同学的眼睛离地面的距离EF为1.6米,求旗杆AB的高度.
第1题图
解:如解图,过点E作EH⊥AB于点H,交CD于点G.
由题意可得四边形EFDG、GDHB都是矩形,AB∥CD∥EF.
∴△ECG∽△EAH,
由题意可得EG=FD=3,GH=BD=30,
CG=CD-GD=CD-EF=5-1.6=3.4,
∴AH=34米,∴AB=AH+HB=34+1.6=35.6米.
答:旗杆AB的高为35.6米.
第1题解图
模型二 中心投影
图形
题设 已知:CG、CD、CE、EF、HE,求AB的高 已知:AD、DG、CH、EF、BE,求DE的长
构建等量关系式 由投影可知△DCG∽△DBA和△FEH∽△FBA,联立两个比例式,可求出BC和AB 由投影可知△AGD∽△ACH和△BFE∽△BCH,列比例式可求得AH、BH,DE=AH+BH-AD-BE
2. 某天晚上,小颖、小华和小林想测量小区门口路灯的高度.如图,相邻的两盏路灯AC、BD高度相等,小颖站在E点处,此时她身后的影子的顶部刚好接触到路灯AC的底部;小华站在F点处,此时他身后影子的顶部刚好接触到路灯BD的底部.这时,小林测得EF=10.2米.已知AB=20米,小颖身高ME=1.6米,小华身高NF=1.75米,AC、BD、ME、NF均与地面垂直.请你根据以上数据计算路灯的高度.(结果精确到0.1米)
第2题图
解:设AE=x,则BF=20-10.2-x=9.8-x,
∵ME∥BD,
∴△AME∽△ADB,
∵NF∥AC, ∴△BNF∽△BCA,
∴BD≈6.8,
答:路灯的高度约为6.8米.
模型三 平行投影
图形
题设 已知:AB、BE、CD,求DF的高 已知:AB、AC、DE、EF,求DG的高
构建等量关系式 直接得出△ABE∽△CDF,列比例式求解 过点F作FH⊥DG,垂足为H,由题知△ABC∽△HFG,求出GH, DG=EF+GH
3. 如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.请你根据以上测量数据,求电线杆AB的高度.
第3题图
解:如解图,过点C作CG⊥AB于点G,则四边形CDBG为矩形,
∴GC=BD=3米,GB=CD=2米.∵∠NMF=∠AGC=90°,NF∥AC,
∴∠NFM=∠ACG,
∴△NMF∽△AGC,
∴AB=AG+GB=6+2=8米,
答:电线杆AB的高为8米.
第3题解图
模型四 镜面反射、投影
图形
题设 已知∠α、AB、AO、OC,求CD的高 已知AB在水中的倒影为BD,及EF、EC、CB,求AB
构建等量关系式 直接得出△ABO∽△CDO,列比例式求解 直接得出△FEC∽△DBC,列比例式求解
4. 小雁塔位于唐长安城安仁坊荐福寺内,又称“荐福寺塔”,是西安的标志性建筑之一.在一次社会实践中,小梅和小鹏想通过测量小雁塔的高度,来检验自己掌握知识和运用知识的能力.如图,由于无法直接到塔的底部,小梅在D处利用测角仪测得塔顶A的仰角为25°,同时小鹏在C、B之间的地面上放置一平面镜(平面镜厚度不计),当小鹏移动平面镜至E处时,小梅恰好通过平面镜看到了塔顶A.经测量,DC=1.5米,CE=3米.已知DC⊥CB,AB⊥CB,且C、E、B在同一条直线上,不考虑其它因素,请你根据题中提供的相关信息,计算小雁塔的高AB.(结果精确到0.1米,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47).
第4题图
解:如解图,过点D作DF⊥AB于点F,则四边形BCDF是矩形,
∴BC=DF,BF=CD=1.5米,
∵∠DEC=∠AEB,∠DCE=∠ABE=90°,∴△DCE∽△ABE,
设AB=x,则BE=2x,∴AF=x-1.5,DF=BC=3+2x,
在Rt△AFD中,tan25°=
解得x≈48.5,即AB≈48.5米,
答:小雁塔的高AB约为48.5米.
第4题解图
模型五 固定视角
图形
题设 已知AB、BC、BE,求BD
构建等量关系式 由一对直角和一锐角相等构造相似三角形,即△ABD∽△CBE,再列比例关系式求解
5. 如图,小明想通过自己所学的知识测量一段笔直的高架桥MN上DQ段的运行距离,设计了如下的测量方案:已知在高架桥的一侧有一排居民楼AB(楼顶AB与高架桥MN在同一水平面上,且AB与点D正好在同一直线上),测得AB=35米,小明先站在A处,测得视线与高架桥MN的垂直距离AH=15米,小明又站在B处,使得视线与BQ在一条直线上,此时测得BQ=45米,且∠QBA=90°,求此高架桥上DQ段的运行距离.
第5题图
解:根据题意得∠AHD=∠QBA=90°,∠ADH=∠QDB,
∴△ADH∽△QDB,
∵AH=15米,BQ=45米,AB=35米,
在Rt△AHD中,根据勾股定理得AD2=AH2+DH2,∴(3DH-35)2=152+DH2,
解得AD=3DH-35.
解得DH=20或DH=6.25(舍去),
答:此高架桥上DQ段的运行距离为75米.
解得DQ=75(米).
陕西5年真题、副题“明”考法
相似三角形的实际应用(5年4考)
命题点
1. (2018陕西20题7分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽,测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C、A共线.已知:CB⊥AD,ED⊥AD,测得BC=1 m,DE=1.5 m,BD=8.5 m,测量示意图
如图所示.请根据相关测量信息,求河宽AB.
第1题图
解:∵CB⊥AD,ED⊥AD,
∴CB∥ED.
又∵∠CAB=∠EAD,∴△ABC∽△ADE,(3分)
∵BC=1 m,DE=1.5 m,BD=8.5 m,AD=AB+BD,
∴AB=17 m,
答:河宽AB为17 m. (7分)
2. (2015陕西20题7分)晚饭后,小聪和小军在社区广场散步.小聪问小军:“你有多高?”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,
AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高
BE的长.(结果精确到0.01米)
第2题图
解:由题意得∠CAD=∠MND=90°,∠CDA=∠MDN,
∴△CAD∽△MND,
∴MN=9.6.(3分)
又∵∠EBF=∠MNF=90°,∠EFB=∠MFN,
∴△EBF∽△MNF,(5分)
解得BE≈1.75.(6分)
答:小军的身高BE约为1.75米.(7分)
3. (2015陕西副题20题7分)周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳篷的宽度.如图,由于无法直接测量,小凯便在楼前地面上选择了一条直线EF,通过在直线EF上选点观测,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳篷A点处;当他位于N′点时,视线从M′点通过D点正好落在遮阳篷B点处.这样观测到的两个点A、B间的距离即为遮阳篷的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、MN、M′N′均垂直于EF,
MN=M′N′,露台的宽CD=GE.测得GE=5米,
EN=12.3米,NN′=6.2米.请你根据以上信息,求出
遮阳篷的宽AB是多少米?(结果精确到0.01米)
第3题图
解:如解图,延长MM′交DE于点P,
∵AG、DE、MN、M′N′均垂直于EF,MN=M′N′,
∴四边形M′MNN′和四边形PMNE均为矩形,
∴MM′=NN′=6.2,PM=EN=12.3.(2分)
∵AB∥CD∥PM,∴△ACD∽△DPM,
△ABD∽△MM′D,
解得AB≈2.52.
答:遮阳篷的宽AB约为2.52米.(7分)
第3题解图
4. (2016陕西20题7分)某市为了打造森林城市,树立城市新地标,实现绿色、共享发展理念,在城南建起了“望月阁”及环阁公园.小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度,来检验自己掌握知识和运用知识的能力.他们经过观察发现,观测点与“望月阁”底部间的距离不易测得,因此经过研究需要两次测量.于是他们首先用平面镜进行测量,方法如下:如图,小芳在小亮和“望月阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C.镜子不动,小亮看着镜面上的标记,他来回走动,走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合.这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米;
然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:如图,小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.
如图,已知:AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计.请你根据题中提供的相关信息,求出“望月阁”的高AB的长度.
第4题图
解:由题意得∠ABC=∠EDC=∠GFH=90°,∠ACB=∠ECD,∠AFB=∠GHF. ∴△ABC∽△EDC,
△ABF∽△GFH,(3分)
解得AB=99米.
答:“望月阁”的高AB为99米.(7分)
5. (2019陕西20题7分)小明想利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学们带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是,他们先在古树周围的空地上选择了一点D,并在点D处安装了测倾器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5 m,并在点G处的地面上水平放置了一个小平面镜,小明沿BG方向移动,当移动到点F时,他刚好在小平
面镜内看到这棵古树的顶端A的像,此时,测得FG=2 m,
小明眼睛与地面的距离EF=1.6 m,测倾器的高CD =0.5 m.
已知点F、G、D、B在同一水平直线上,且EF、CD、AB均
垂直于FB,求这棵古树的高AB.(小平面镜的大小忽略不计)
第5题图
解:如解图,过点C作CH⊥AB于点H,则CH=BD,BH=CD=0.5.(1分)
在Rt△ACH中,∠ACH=45°,∴AH=CH=BD.
∴AB=AH+BH=BD+0.5.(2分)
∵EF⊥FB,AB⊥FB,∴∠EFG=∠ABG=90°.
由题意,易知∠EGF=∠AGB,
∴△EFG∽△ABG.(4分)
解得BD=17.5 m.(6分)
∴AB=17.5+0.5=18(m).
答:这棵古树的高AB为18 m.(7分)
第5题解图
6. (2019陕西副题20题7分)新学期,小华和小明被选为升旗手,为了更好地完成升旗任务,他俩想利用测倾器和阳光下的影子来测量学校旗杆的高度PA.如图所示,旗杆直立于旗台上的点P处,他们的测量方法是:首先,在阳光下,小华站在旗杆影子的顶端F处,此时,量得小华的影长FG=2 m,小华身高EF=1.6 m;然后,在旗杆影子上的点D处,安装测倾器CD,测得旗杆顶端A的仰角为49°,量得CD=0.6 m,DF=6 m,旗台高BP=1.2 m.已知在测量过程中,点B、D、F、G在同一水平直线上,点A、P、B在同一条直线上,
AB、CD、EF均垂直于BG.求旗杆的高度PA.
(参考数据:sin49°≈0.8,cos49°≈0.7,tan49°≈1.2)
第6题图
解:如解图,过点C作CH⊥AB于点H,则CH=BD,BH=CD=0.6.
在Rt△AHC中,tan49°=
∴AH=1.2BD.
∴AB=AH+HB=1.2BD+0.6.(3分)
连接AF、EG.由题意,可得△EFG∽△ABF.
解得BD=10.5,∴AB=13.2.(6分) ∴PA=AB-PB=13.2-1.2=12(m).
答:旗杆的高度PA约为12 m.(7分)
第6题解图
点击链接至练习册
同课章节目录
