【中考数学总复习】第16课时 三角形及其性质 课件
文档属性
| 名称 | 【中考数学总复习】第16课时 三角形及其性质 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 14:50:29 | ||
图片预览





文档简介
(共18张PPT)
第四单元 三角形
第16课时 三角形及其性质
(5年1考,3分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
中考试题中的数学文化
4
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:七下第四章P81-P91,八上第七章P178-P183,
八下第六章P150-P152;
人教:八上第十一章P1-P18.
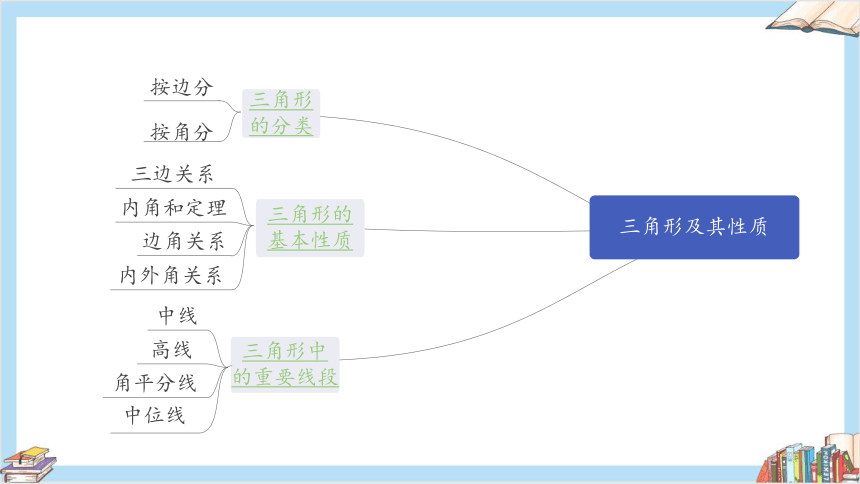
三角形中
的重要线段
三角形的
基本性质
三角形
的分类
按边分
按角分
高线
角平分线
中线
中位线
内角和定理
边角关系
三边关系
内外角关系
三角形及其性质
三角形的分类
考点
1
三角形
三边各不相等的三角形
等腰三角形
“底边≠腰”的等腰三角形
等边三角形
1. 按边分
2. 按角分:锐角三角形、直角三角形、钝角三角形.
返回思维导图
三角形的基本性质
考点
2
1. 三边关系:三角形两边之和______第三边,两边之差________第三边.若一个三角形的三边长分别为a、b、c,则|a-b|2. 内角和定理:三角形三个内角的和等于________.
3. 内外角关系:
(1)三角形的任意一个外角________与它不相邻的两个内角之和;
(2)三角形的任意一个外角________任何一个与它不相邻的内角.
4. 边角关系:在同一个三角形中,等边对等角,大边对______,小边对小角.
大于
小于
180°
等于
大于
大角
返回思维导图
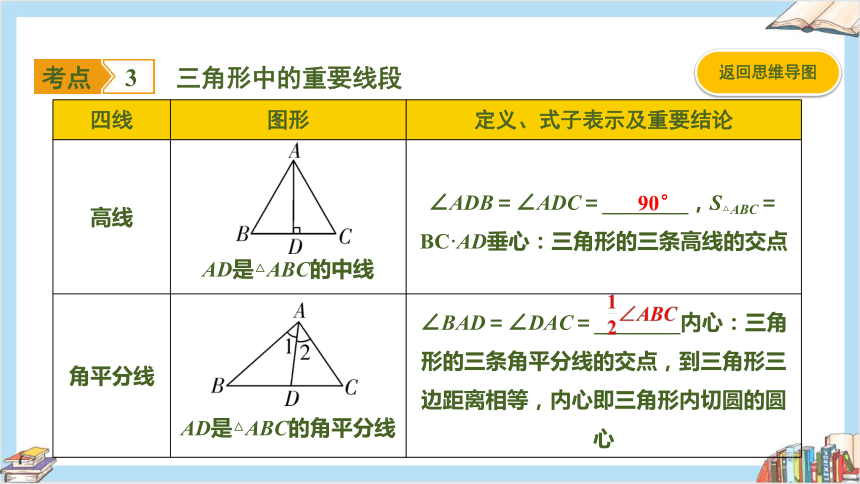
三角形中的重要线段
考点
3
四线 图形 定义、式子表示及重要结论
高线 AD是△ABC的中线 ∠ADB=∠ADC=________,S△ABC=BC·AD垂心:三角形的三条高线的交点
角平分线 AD是△ABC的角平分线 ∠BAD=∠DAC=________内心:三角形的三条角平分线的交点,到三角形三边距离相等,内心即三角形内切圆的圆心
90°
返回思维导图
四线 图形 定义、式子表示及重要结论
中线 AD是△ABC的中线 BD=DC=________,
S△ABD=S△ADC= S△ABC
重心:三角形三条中线的交点
中位线 DE是△ABC的中位线 AD=DB,AE=EC,______∥BC,且______= BC
DE
DE
返回思维导图
【提分要点】当三角形中遇到中点时,常构造三角形的中位线,利用其证明线段平行或倍分问题,可简单地概括为“已知中点找中位线”;在平行四边形或菱形中,边上有中点时,可连接中点与对角线的交点构造中位线.
返回思维导图
回归教材
证明:三角形的内角和等于180°.
1. 已知:如图,△ABC是任意一个三角形.
求证:∠A+∠B+∠C=180°.
【自主解答】
第1题图
证明:如解图①,延长BC至点D,过点C作射线CE∥BA,
则∠1=∠A(两直线平行,内错角相等),
∠2=∠B(两直线平行,同位角相等).
∵∠1+∠2+∠ACB=180°(平角的定义),
∴∠A+∠B+∠ACB=180°(等量代换).
第1题解图①
【以下方法源自人教八上P12】
证明:如解图②,过点A作直线PQ∥BC,
则∠1=∠B,∠2=∠C,
∵∠1+∠BAC+∠2=180°,
∴∠B+∠BAC+∠C=180°.
第1题解图②
2. 已知:如图,DE是△ABC的中位线.
求证:DE∥BC,DE= BC.
【自主解答】
第2题图
证明:三角形的中位线平行于第三边,且等于第三边的一半.
证明:如解图,延长DE至点F,使FE=DE,连接CF.
在△ADE和△CFE中,
∵AE=CE,∠1=∠2,DE=FE,
∴△ADE≌△CFE(SAS).∴∠A=∠ECF,AD=CF.
∴CF∥AB.
∵BD=AD,∴CF=BD.
∴四边形DBCF是平行四边形(一组对边平行且相等的四边形是平行四边形).
∴DF∥BC(平行四边形的定义),DF=BC(平行四边形的对边相等).
第2题解图
典例“串”考点
例 如图,在△ABC中,点D是BC边上一点,点E是AC边上一点,连接AD、DE.
例题图
(1)当AD是∠BAC的平分线.
①若∠BAC=80°,∠B=50°,则∠C=______,∠ADC=______;
②若AC=4,△ADC的面积为6,点D到AB的距离是________.
50°
90°
3
(2)当DE垂直平分AC.
①若AB+BC=10,则△ABD的周长为________;
②若∠C=30°,∠B=50°,则∠BAD的度数为________.
(3)当点D为BC的中点,DE∥AB.
①若△ABC的面积为24,则△ADC的面积为______,连接BE,则△ABE的面积为________;
②△ADE的周长为12,AD=5,AC=6,则AB的长为________.
10
70°
12
12
8
陕西5年真题、副题“明”考法
三角形中的重要线段(2017.12A,常在尺规作图中考查)
命题点
1. (2015陕西副题6题3分)如图,点P是△ABC内一点,且PA=PB=PC,则点P是( )
A. △ABC三边垂直平分线的交点
B. △ABC三条角平分线的交点
C. △ABC三条高线的交点
D. △ABC三条中线的交点
第1题图
A
2. (2017陕西副题6题3分)如图,在△ABC中,∠A=60°,∠B=45°.若边AC的垂直平分线DE交边AB于点D,交边AC于点E,连接CD,则∠DCB=( )
A. 15° B. 20°
C. 25° D. 30°
A
第2题图
3. (2017陕西12A题3分)如图,在△ABC中,BD和CE是△ABC的两条角平分线.若∠A=52°,则∠1+∠2的度数为________.
第3题图
64°
点击链接至练习册
第四单元 三角形
第16课时 三角形及其性质
(5年1考,3分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
中考试题中的数学文化
4
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:七下第四章P81-P91,八上第七章P178-P183,
八下第六章P150-P152;
人教:八上第十一章P1-P18.
三角形中
的重要线段
三角形的
基本性质
三角形
的分类
按边分
按角分
高线
角平分线
中线
中位线
内角和定理
边角关系
三边关系
内外角关系
三角形及其性质
三角形的分类
考点
1
三角形
三边各不相等的三角形
等腰三角形
“底边≠腰”的等腰三角形
等边三角形
1. 按边分
2. 按角分:锐角三角形、直角三角形、钝角三角形.
返回思维导图
三角形的基本性质
考点
2
1. 三边关系:三角形两边之和______第三边,两边之差________第三边.若一个三角形的三边长分别为a、b、c,则|a-b|
3. 内外角关系:
(1)三角形的任意一个外角________与它不相邻的两个内角之和;
(2)三角形的任意一个外角________任何一个与它不相邻的内角.
4. 边角关系:在同一个三角形中,等边对等角,大边对______,小边对小角.
大于
小于
180°
等于
大于
大角
返回思维导图
三角形中的重要线段
考点
3
四线 图形 定义、式子表示及重要结论
高线 AD是△ABC的中线 ∠ADB=∠ADC=________,S△ABC=BC·AD垂心:三角形的三条高线的交点
角平分线 AD是△ABC的角平分线 ∠BAD=∠DAC=________内心:三角形的三条角平分线的交点,到三角形三边距离相等,内心即三角形内切圆的圆心
90°
返回思维导图
四线 图形 定义、式子表示及重要结论
中线 AD是△ABC的中线 BD=DC=________,
S△ABD=S△ADC= S△ABC
重心:三角形三条中线的交点
中位线 DE是△ABC的中位线 AD=DB,AE=EC,______∥BC,且______= BC
DE
DE
返回思维导图
【提分要点】当三角形中遇到中点时,常构造三角形的中位线,利用其证明线段平行或倍分问题,可简单地概括为“已知中点找中位线”;在平行四边形或菱形中,边上有中点时,可连接中点与对角线的交点构造中位线.
返回思维导图
回归教材
证明:三角形的内角和等于180°.
1. 已知:如图,△ABC是任意一个三角形.
求证:∠A+∠B+∠C=180°.
【自主解答】
第1题图
证明:如解图①,延长BC至点D,过点C作射线CE∥BA,
则∠1=∠A(两直线平行,内错角相等),
∠2=∠B(两直线平行,同位角相等).
∵∠1+∠2+∠ACB=180°(平角的定义),
∴∠A+∠B+∠ACB=180°(等量代换).
第1题解图①
【以下方法源自人教八上P12】
证明:如解图②,过点A作直线PQ∥BC,
则∠1=∠B,∠2=∠C,
∵∠1+∠BAC+∠2=180°,
∴∠B+∠BAC+∠C=180°.
第1题解图②
2. 已知:如图,DE是△ABC的中位线.
求证:DE∥BC,DE= BC.
【自主解答】
第2题图
证明:三角形的中位线平行于第三边,且等于第三边的一半.
证明:如解图,延长DE至点F,使FE=DE,连接CF.
在△ADE和△CFE中,
∵AE=CE,∠1=∠2,DE=FE,
∴△ADE≌△CFE(SAS).∴∠A=∠ECF,AD=CF.
∴CF∥AB.
∵BD=AD,∴CF=BD.
∴四边形DBCF是平行四边形(一组对边平行且相等的四边形是平行四边形).
∴DF∥BC(平行四边形的定义),DF=BC(平行四边形的对边相等).
第2题解图
典例“串”考点
例 如图,在△ABC中,点D是BC边上一点,点E是AC边上一点,连接AD、DE.
例题图
(1)当AD是∠BAC的平分线.
①若∠BAC=80°,∠B=50°,则∠C=______,∠ADC=______;
②若AC=4,△ADC的面积为6,点D到AB的距离是________.
50°
90°
3
(2)当DE垂直平分AC.
①若AB+BC=10,则△ABD的周长为________;
②若∠C=30°,∠B=50°,则∠BAD的度数为________.
(3)当点D为BC的中点,DE∥AB.
①若△ABC的面积为24,则△ADC的面积为______,连接BE,则△ABE的面积为________;
②△ADE的周长为12,AD=5,AC=6,则AB的长为________.
10
70°
12
12
8
陕西5年真题、副题“明”考法
三角形中的重要线段(2017.12A,常在尺规作图中考查)
命题点
1. (2015陕西副题6题3分)如图,点P是△ABC内一点,且PA=PB=PC,则点P是( )
A. △ABC三边垂直平分线的交点
B. △ABC三条角平分线的交点
C. △ABC三条高线的交点
D. △ABC三条中线的交点
第1题图
A
2. (2017陕西副题6题3分)如图,在△ABC中,∠A=60°,∠B=45°.若边AC的垂直平分线DE交边AB于点D,交边AC于点E,连接CD,则∠DCB=( )
A. 15° B. 20°
C. 25° D. 30°
A
第2题图
3. (2017陕西12A题3分)如图,在△ABC中,BD和CE是△ABC的两条角平分线.若∠A=52°,则∠1+∠2的度数为________.
第3题图
64°
点击链接至练习册
同课章节目录
