【中考数学总复习】第21课时 锐角三角函数及其实际应用 课件
文档属性
| 名称 | 【中考数学总复习】第21课时 锐角三角函数及其实际应用 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 14:50:29 | ||
图片预览






文档简介
(共32张PPT)
第四单元 三角形
第21课时 锐角三角函数及其实际应用
(每年必考1道,3分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:九下第一章P1-P27;
人教:八下第十七章P21-P39,九下第二十八章P60-P85.
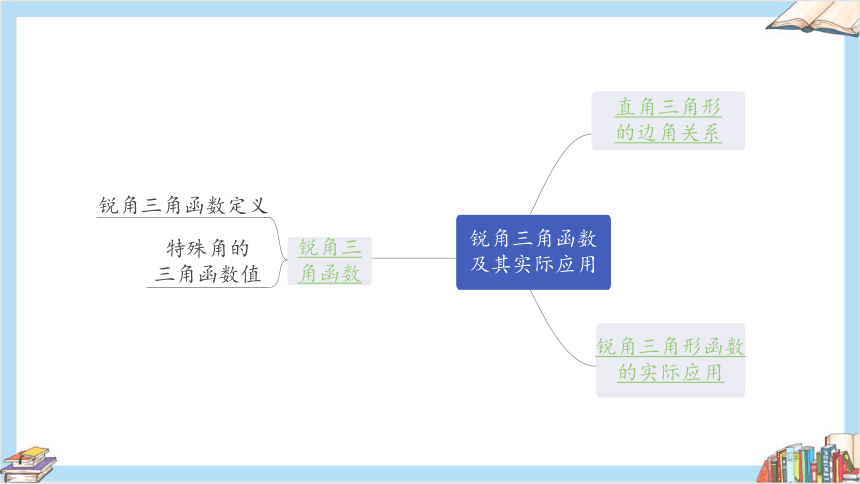
锐角三
角函数
直角三角形
的边角关系
锐角三角形函数
的实际应用
锐角三角函数定义
特殊角的
三角函数值
锐角三角函数
及其实际应用
锐角三角函数
考点
1
1. 锐角三角函数的定义
图①
如图①,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦,记作sinA.
sinA=斜边(∠A的对边)=________.
∠A的余弦:cosA=斜边(∠A的邻边)=________.
∠A的正切:tanA=∠A的邻边(∠A的对边)=________.
返回思维导图
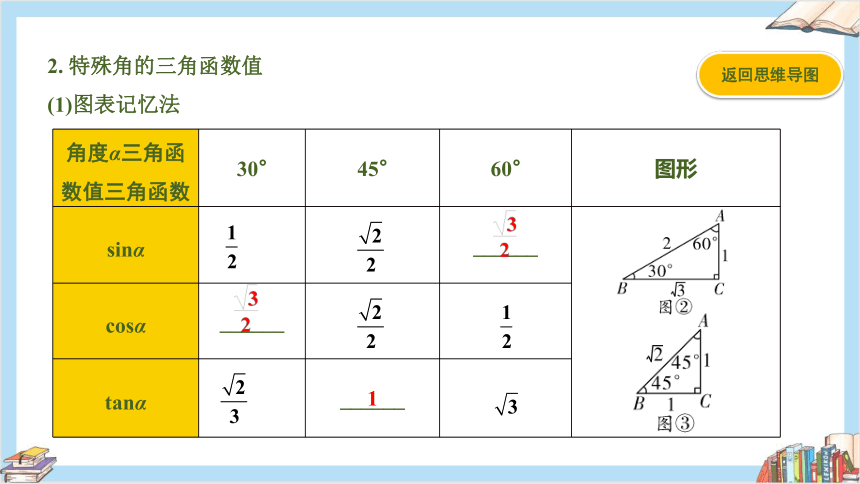
2. 特殊角的三角函数值
(1)图表记忆法
角度α三角函数值三角函数 30° 45° 60° 图形
sinα ______
cosα ______ tanα ______ 1
返回思维导图
(2)规律记忆法:30°、45°、60°角的正弦值的分母都是2,分子依次为1、 、 ;30°、45°、60°角的余弦值恰好是60°、45°、30°角的正弦值.
返回思维导图
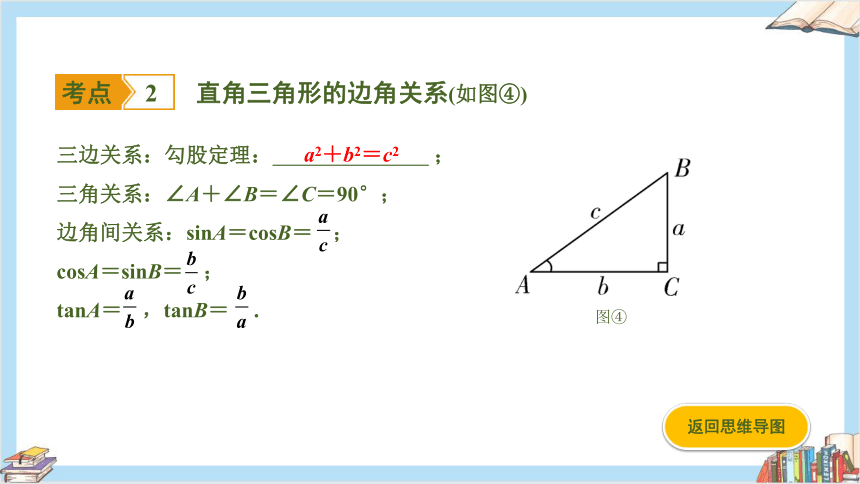
直角三角形的边角关系(如图④)
考点
2
三边关系:勾股定理: ;
三角关系:∠A+∠B=∠C=90°;
边角间关系:sinA=cosB= ;
cosA=sinB= ;
tanA= ,tanB= .
a2+b2=c2
图④
返回思维导图
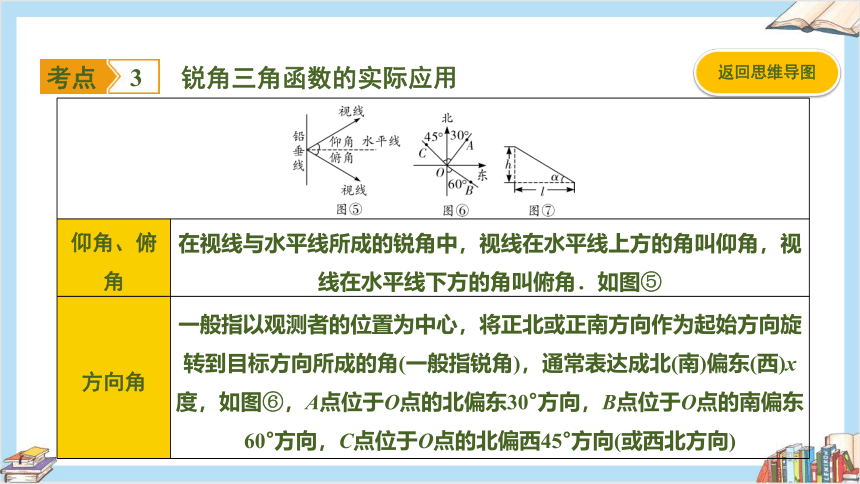
锐角三角函数的实际应用
考点
3
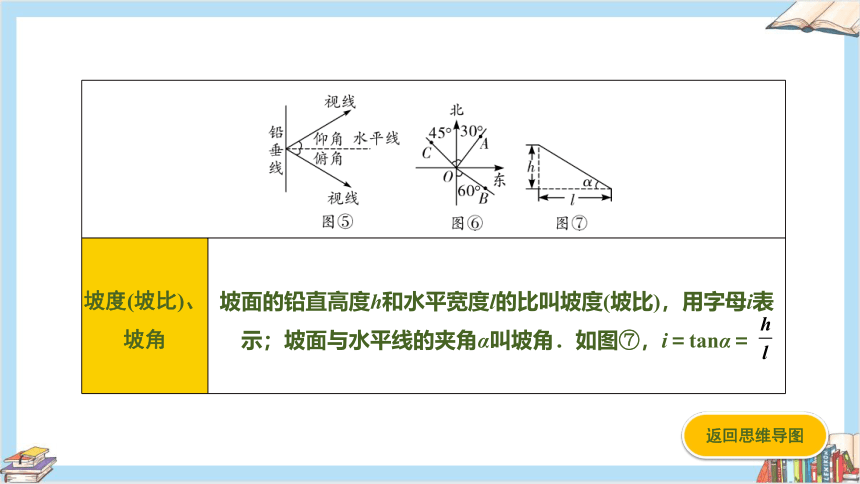
仰角、俯角 在视线与水平线所成的锐角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角.如图⑤
方向角 一般指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标方向所成的角(一般指锐角),通常表达成北(南)偏东(西)x度,如图⑥,A点位于O点的北偏东30°方向,B点位于O点的南偏东60°方向,C点位于O点的北偏西45°方向(或西北方向)
返回思维导图
坡度(坡比)、坡角 坡面的铅直高度h和水平宽度l的比叫坡度(坡比),用字母i表示;坡面与水平线的夹角α叫坡角.如图⑦,i=tanα=
返回思维导图
典例“串”考点
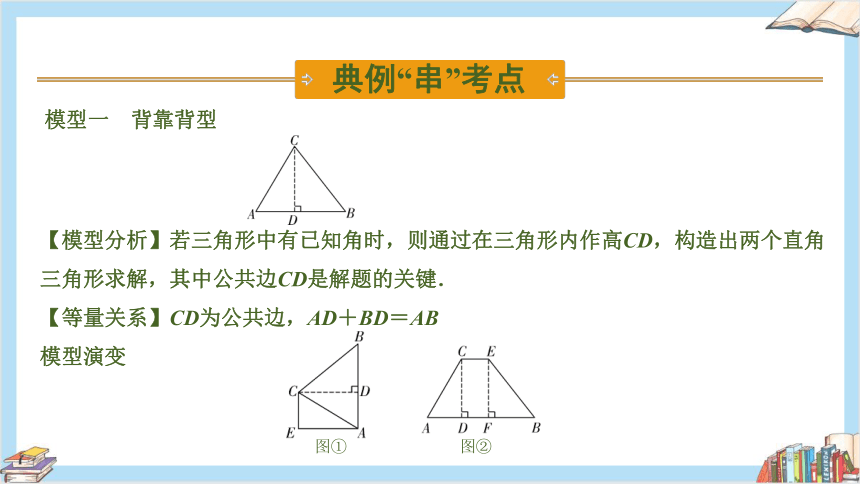
模型一 背靠背型
【模型分析】若三角形中有已知角时,则通过在三角形内作高CD,构造出两个直角三角形求解,其中公共边CD是解题的关键.
【等量关系】CD为公共边,AD+BD=AB
模型演变
图①
图②
【等量关系】如图①,CE=DA,CD=EA,CE+BD=AB;如图②,CD=EF,CE=DF,AD+CE+BF=AB.
1. 周六下午,王武和父亲开车出去办事.如图,他们在A处测得其北偏东30°处有一座移动信号发射塔C,当车以每小时60公里的速度向正东方向行驶10分钟到达B处后,此时他们测得信号发射塔C在其北偏西15°处,请你求出此时车和发射塔之间的距离BC.(结果保留根号)
第1题图
解:如解图,过点B作BD⊥AC于点D,则∠BDA=∠BDC=90°,
∠BAC=90°-30°=60°,∠ABC=90°-15°=75°,
∴∠ABD=30°,
∴∠CBD=45°,AD=
∵∠C=180°-∠BAC-∠ABC=45°,
∴△BCD是等腰直角三角形,
第1题解图
2. 小婷在放学路上,看到隧道上方有一块宣传“垃圾分类从我做起”的竖直标语牌CD.如图,她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10 m,隧道高6.5 m(即BC=6.5 m),求标语牌CD的高(结果精确到0.1米,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90, ≈1.73)
第2题图
解:如解图,过点A作AE⊥BD于点E.
在Rt△AEB中,∵∠EAB=30°,AB=10 m,
∴BE= AB=5 m,AE= m,
在Rt△ADE中,DE=AE·tan42°≈7.79 m,
∴BD=DE+BE≈12.79 m,
∴CD=BD-BC≈12.79-6.5≈6.3 m,
答:标语牌CD的高约为6.3 m.
第2题解图
模型二 母子型
图①
图②
【模型分析】若三角形中有已知角,通过在三角形外作垂线BC,构造有公共直角的两个三角形求解,其中公共边BC是解题的关键.
【等量关系】BC为公共边,如图①,AD+DC=AC;如图②,DC-BC=DB.
图③
图④
模型演变1
【等量关系】如图③,DF=EC,DE=FC,BF+DE=BC,AE+DF=AC;如图④,AF=CE,AC=FE,BC+AF=BE.
模型演变2
图⑤
图⑥
图⑦
【等量关系】如图⑤,BE+EC=BC;如图⑥,EC-BC=BE;如图⑦,AC=FG,AF=CG,AD+DC=FG,BC+AF=BG.
图⑧
图⑨
【等量关系】如图⑧,BC=FG,BF=CG,AC+BF=AG,EF+BC=EG;如图⑨,BC=FG,BF=CG,EF+BC=EG,BD+DF=BF,AC+BD+DF=AG.
模型演变3
3. (2019湘潭)我国于2019年6月5日首次完成运载火箭海上发射,这标志着我国火箭发射技术达到了一个崭新的高度.如图,运载火箭从海面发射站点M处垂直海面发射,当火箭到达点A处时,海岸边N处的雷达站测得点N到点A的距离为8千米,仰角为30°.火箭继续直线上升到达点B处,此时海岸边N处的雷达测得B处的仰角增加15°,求此时火箭所在点B处与发射站点M处的距离.(结果精确到0.1千米)(参考数据: ≈1.41, ≈1.73)
第3题图
解:在Rt△AMN中,cos∠ANM= ,
∵∠ANM=30°,AN=8,
∴MN=AN·cos∠ANM=8cos30°=
在Rt△BMN中,∠BNM=45°,
∴MB=MN= ≈4×1.73≈6.9(千米).
答:此时火箭所在点B处与发射站点M处的距离约为6.9千米.
4. (2019陕师大附中模拟)某校在“建设特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C处测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E处测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度.(结果精确到0.1米,参考数据: ≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
第4题图
解:如解图,过点C作CN⊥BM于点N,则四边形CDMN是矩形,点E在线段CN上.
∴BN=BM-CD=17-1=16米,
在Rt△BCN中,BN=16米,∠BEN=37°,
在Rt△AEN中,∵EN=CN-CE≈17.33米,∠AEN=45°,
∴AN=EN·tan45°≈17.33米,
∴AB=AN-BN≈17.33-16≈1.3米.
答:宣传牌AB的高度约为1.3米.
第4题解图
模型三 拥抱型
【模型分析】分别解两个直角三角形,其中公共边BC是解题的关键.
【等量关系】BC为公共边
【模型演变】
图①
图②
图③
【等量关系】如图①,BF+FC+CE=BE;如图②,BC+CE=BE;如图③,
AB=GE,AG=BE,BC+CE=AG,DG+AB=DE.
5. (2019西安铁一中模拟)如图所示,某数学活动小组为了测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是60°,若坡角∠FAE=30°,求大树的高度.
第5题图
解:如解图,过点D作DG⊥BC于点G,则DG∥EC.
∵∠FAE=30°,∠BAC=60°,
∴∠ADG=30°,∠DAB=90°.
又∵∠BDG=30°.
∴∠BDA=∠BDG+∠ADG=60°.
在Rt△ABD中,AD=6米,
∴AB=AD·tan∠BDA= (米).
在Rt△ABC中,BC=AB·sin∠BAC=
答:大树的高度为9米.
第5题解图
陕西5年真题、副题“明”考法
锐角三角函数的实际应用(5年2考)
注:2018年开始陕西中考取消使用科学计算器,为了计算简便,以下真题参考数据统一改为两位小数.
命题点
类型一 仰角、俯角(2017.20)
1. (2018陕西副题20题7分)如图所示,某集团的项目组计划在山脚下A点与山顶B点之间修建一条索道,现利用无人机测算A、B两点间的距离.无人机飞至山顶点B的正上方点C处时,测得山脚下A点的俯角约为45°,C点与A点的高度差为400 m,BC=100 m,求山脚下A点到山顶B点的距离AB.
第1题图
解:如解图,延长CB与A点所在水平面相交于点D,
由题意,知CD⊥AD,CD=400,∠CAD=45°.∴AD=CD=400.(2分)
∵CB=100,∴BD=CD-BC=300.(4分)
在Rt△ABD中,
=500 m.
答:山脚下A点到山顶B点的距离AB为500 m.(7分)
第1题解图
2. (2017陕西20题7分)某市一湖的湖心岛有一棵百年古树,当地人称它为“乡思柳”,不乘船不易到达,每年初春时节,人们喜欢在“聚贤亭”观湖赏柳.小红和小军很想知道“聚贤亭”与“乡思柳”之间的大致距离,于是,有一天,他们俩带着测倾器和皮尺来测量这个距离.测量方案如下:如图,首先,小军站在“聚贤亭”的A处,用测倾器测得“乡思柳”顶端M点的仰角为23°,此时测得小军的眼睛距地面的高度AB为1.7米;然后,小军在A处蹲下,用测倾器测得“乡思柳”顶端M点的仰角为24°,这时测得小军的眼睛距地面的高度AC为 1米.请你利用以上所测得的数据,计算“聚贤亭”与“乡思柳”之间的距离AN的长(结果
精确到1米).(参考数据:sin23°≈0.39,cos23°≈0.92,
tan23°≈0.42,sin24°≈0.41,cos24°≈0.91,tan24°≈0.45)
第2题图
解:如解图,过点B作BD⊥MN,垂足为D,过点C作CE⊥MN,垂足为E.
设AN=x米,则BD=CE=x米,
在Rt△MBD中,MD=x·tan23°.
在Rt△MCE中,ME=x·tan24°.(4分)
∵ME-MD=DE=BC,
∴x·tan24°-x·tan23°=1.7-1,
解得x≈23.
答:“聚贤亭”与“乡思柳”之间的距离AN的长约为23米.(7分)
第2题解图
类型二 方向角
3. (2016陕西副题20题7分)某市为了创建绿色生态城市,在城东建了“东州湖”景区.小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.请你根据以上提供的信息,计算“东州湖”东西
两端之间AB的长.(结果精确到 1米)
(参考数据:sin73°≈0.96,cos73°≈0.29,
tan73°≈3.27, ≈1.41)
第3题图
解:在Rt△BCD中,∠BCD=45°,BC=350米,
∴BD=BC·sin∠BCD=350·sin45°= 米,(3分)
∴CD=BD= 米,
在Rt△ACD中,∠ACD=73°,
∴AD=CD·tan∠ACD= · tan73°米,(5分)
∴AB=AD+BD= ·tan73°+ ≈1054(米).
答:“东州湖”东西两端之间AB的长约为1054米.(7分)
点击链接至练习册
第四单元 三角形
第21课时 锐角三角函数及其实际应用
(每年必考1道,3分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:九下第一章P1-P27;
人教:八下第十七章P21-P39,九下第二十八章P60-P85.
锐角三
角函数
直角三角形
的边角关系
锐角三角形函数
的实际应用
锐角三角函数定义
特殊角的
三角函数值
锐角三角函数
及其实际应用
锐角三角函数
考点
1
1. 锐角三角函数的定义
图①
如图①,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦,记作sinA.
sinA=斜边(∠A的对边)=________.
∠A的余弦:cosA=斜边(∠A的邻边)=________.
∠A的正切:tanA=∠A的邻边(∠A的对边)=________.
返回思维导图
2. 特殊角的三角函数值
(1)图表记忆法
角度α三角函数值三角函数 30° 45° 60° 图形
sinα ______
cosα ______ tanα ______ 1
返回思维导图
(2)规律记忆法:30°、45°、60°角的正弦值的分母都是2,分子依次为1、 、 ;30°、45°、60°角的余弦值恰好是60°、45°、30°角的正弦值.
返回思维导图
直角三角形的边角关系(如图④)
考点
2
三边关系:勾股定理: ;
三角关系:∠A+∠B=∠C=90°;
边角间关系:sinA=cosB= ;
cosA=sinB= ;
tanA= ,tanB= .
a2+b2=c2
图④
返回思维导图
锐角三角函数的实际应用
考点
3
仰角、俯角 在视线与水平线所成的锐角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角.如图⑤
方向角 一般指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标方向所成的角(一般指锐角),通常表达成北(南)偏东(西)x度,如图⑥,A点位于O点的北偏东30°方向,B点位于O点的南偏东60°方向,C点位于O点的北偏西45°方向(或西北方向)
返回思维导图
坡度(坡比)、坡角 坡面的铅直高度h和水平宽度l的比叫坡度(坡比),用字母i表示;坡面与水平线的夹角α叫坡角.如图⑦,i=tanα=
返回思维导图
典例“串”考点
模型一 背靠背型
【模型分析】若三角形中有已知角时,则通过在三角形内作高CD,构造出两个直角三角形求解,其中公共边CD是解题的关键.
【等量关系】CD为公共边,AD+BD=AB
模型演变
图①
图②
【等量关系】如图①,CE=DA,CD=EA,CE+BD=AB;如图②,CD=EF,CE=DF,AD+CE+BF=AB.
1. 周六下午,王武和父亲开车出去办事.如图,他们在A处测得其北偏东30°处有一座移动信号发射塔C,当车以每小时60公里的速度向正东方向行驶10分钟到达B处后,此时他们测得信号发射塔C在其北偏西15°处,请你求出此时车和发射塔之间的距离BC.(结果保留根号)
第1题图
解:如解图,过点B作BD⊥AC于点D,则∠BDA=∠BDC=90°,
∠BAC=90°-30°=60°,∠ABC=90°-15°=75°,
∴∠ABD=30°,
∴∠CBD=45°,AD=
∵∠C=180°-∠BAC-∠ABC=45°,
∴△BCD是等腰直角三角形,
第1题解图
2. 小婷在放学路上,看到隧道上方有一块宣传“垃圾分类从我做起”的竖直标语牌CD.如图,她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10 m,隧道高6.5 m(即BC=6.5 m),求标语牌CD的高(结果精确到0.1米,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90, ≈1.73)
第2题图
解:如解图,过点A作AE⊥BD于点E.
在Rt△AEB中,∵∠EAB=30°,AB=10 m,
∴BE= AB=5 m,AE= m,
在Rt△ADE中,DE=AE·tan42°≈7.79 m,
∴BD=DE+BE≈12.79 m,
∴CD=BD-BC≈12.79-6.5≈6.3 m,
答:标语牌CD的高约为6.3 m.
第2题解图
模型二 母子型
图①
图②
【模型分析】若三角形中有已知角,通过在三角形外作垂线BC,构造有公共直角的两个三角形求解,其中公共边BC是解题的关键.
【等量关系】BC为公共边,如图①,AD+DC=AC;如图②,DC-BC=DB.
图③
图④
模型演变1
【等量关系】如图③,DF=EC,DE=FC,BF+DE=BC,AE+DF=AC;如图④,AF=CE,AC=FE,BC+AF=BE.
模型演变2
图⑤
图⑥
图⑦
【等量关系】如图⑤,BE+EC=BC;如图⑥,EC-BC=BE;如图⑦,AC=FG,AF=CG,AD+DC=FG,BC+AF=BG.
图⑧
图⑨
【等量关系】如图⑧,BC=FG,BF=CG,AC+BF=AG,EF+BC=EG;如图⑨,BC=FG,BF=CG,EF+BC=EG,BD+DF=BF,AC+BD+DF=AG.
模型演变3
3. (2019湘潭)我国于2019年6月5日首次完成运载火箭海上发射,这标志着我国火箭发射技术达到了一个崭新的高度.如图,运载火箭从海面发射站点M处垂直海面发射,当火箭到达点A处时,海岸边N处的雷达站测得点N到点A的距离为8千米,仰角为30°.火箭继续直线上升到达点B处,此时海岸边N处的雷达测得B处的仰角增加15°,求此时火箭所在点B处与发射站点M处的距离.(结果精确到0.1千米)(参考数据: ≈1.41, ≈1.73)
第3题图
解:在Rt△AMN中,cos∠ANM= ,
∵∠ANM=30°,AN=8,
∴MN=AN·cos∠ANM=8cos30°=
在Rt△BMN中,∠BNM=45°,
∴MB=MN= ≈4×1.73≈6.9(千米).
答:此时火箭所在点B处与发射站点M处的距离约为6.9千米.
4. (2019陕师大附中模拟)某校在“建设特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C处测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E处测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度.(结果精确到0.1米,参考数据: ≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
第4题图
解:如解图,过点C作CN⊥BM于点N,则四边形CDMN是矩形,点E在线段CN上.
∴BN=BM-CD=17-1=16米,
在Rt△BCN中,BN=16米,∠BEN=37°,
在Rt△AEN中,∵EN=CN-CE≈17.33米,∠AEN=45°,
∴AN=EN·tan45°≈17.33米,
∴AB=AN-BN≈17.33-16≈1.3米.
答:宣传牌AB的高度约为1.3米.
第4题解图
模型三 拥抱型
【模型分析】分别解两个直角三角形,其中公共边BC是解题的关键.
【等量关系】BC为公共边
【模型演变】
图①
图②
图③
【等量关系】如图①,BF+FC+CE=BE;如图②,BC+CE=BE;如图③,
AB=GE,AG=BE,BC+CE=AG,DG+AB=DE.
5. (2019西安铁一中模拟)如图所示,某数学活动小组为了测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是60°,若坡角∠FAE=30°,求大树的高度.
第5题图
解:如解图,过点D作DG⊥BC于点G,则DG∥EC.
∵∠FAE=30°,∠BAC=60°,
∴∠ADG=30°,∠DAB=90°.
又∵∠BDG=30°.
∴∠BDA=∠BDG+∠ADG=60°.
在Rt△ABD中,AD=6米,
∴AB=AD·tan∠BDA= (米).
在Rt△ABC中,BC=AB·sin∠BAC=
答:大树的高度为9米.
第5题解图
陕西5年真题、副题“明”考法
锐角三角函数的实际应用(5年2考)
注:2018年开始陕西中考取消使用科学计算器,为了计算简便,以下真题参考数据统一改为两位小数.
命题点
类型一 仰角、俯角(2017.20)
1. (2018陕西副题20题7分)如图所示,某集团的项目组计划在山脚下A点与山顶B点之间修建一条索道,现利用无人机测算A、B两点间的距离.无人机飞至山顶点B的正上方点C处时,测得山脚下A点的俯角约为45°,C点与A点的高度差为400 m,BC=100 m,求山脚下A点到山顶B点的距离AB.
第1题图
解:如解图,延长CB与A点所在水平面相交于点D,
由题意,知CD⊥AD,CD=400,∠CAD=45°.∴AD=CD=400.(2分)
∵CB=100,∴BD=CD-BC=300.(4分)
在Rt△ABD中,
=500 m.
答:山脚下A点到山顶B点的距离AB为500 m.(7分)
第1题解图
2. (2017陕西20题7分)某市一湖的湖心岛有一棵百年古树,当地人称它为“乡思柳”,不乘船不易到达,每年初春时节,人们喜欢在“聚贤亭”观湖赏柳.小红和小军很想知道“聚贤亭”与“乡思柳”之间的大致距离,于是,有一天,他们俩带着测倾器和皮尺来测量这个距离.测量方案如下:如图,首先,小军站在“聚贤亭”的A处,用测倾器测得“乡思柳”顶端M点的仰角为23°,此时测得小军的眼睛距地面的高度AB为1.7米;然后,小军在A处蹲下,用测倾器测得“乡思柳”顶端M点的仰角为24°,这时测得小军的眼睛距地面的高度AC为 1米.请你利用以上所测得的数据,计算“聚贤亭”与“乡思柳”之间的距离AN的长(结果
精确到1米).(参考数据:sin23°≈0.39,cos23°≈0.92,
tan23°≈0.42,sin24°≈0.41,cos24°≈0.91,tan24°≈0.45)
第2题图
解:如解图,过点B作BD⊥MN,垂足为D,过点C作CE⊥MN,垂足为E.
设AN=x米,则BD=CE=x米,
在Rt△MBD中,MD=x·tan23°.
在Rt△MCE中,ME=x·tan24°.(4分)
∵ME-MD=DE=BC,
∴x·tan24°-x·tan23°=1.7-1,
解得x≈23.
答:“聚贤亭”与“乡思柳”之间的距离AN的长约为23米.(7分)
第2题解图
类型二 方向角
3. (2016陕西副题20题7分)某市为了创建绿色生态城市,在城东建了“东州湖”景区.小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.请你根据以上提供的信息,计算“东州湖”东西
两端之间AB的长.(结果精确到 1米)
(参考数据:sin73°≈0.96,cos73°≈0.29,
tan73°≈3.27, ≈1.41)
第3题图
解:在Rt△BCD中,∠BCD=45°,BC=350米,
∴BD=BC·sin∠BCD=350·sin45°= 米,(3分)
∴CD=BD= 米,
在Rt△ACD中,∠ACD=73°,
∴AD=CD·tan∠ACD= · tan73°米,(5分)
∴AB=AD+BD= ·tan73°+ ≈1054(米).
答:“东州湖”东西两端之间AB的长约为1054米.(7分)
点击链接至练习册
同课章节目录
