【中考数学总复习】第24课时 圆的基本性质 课件
文档属性
| 名称 | 【中考数学总复习】第24课时 圆的基本性质 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 14:50:29 | ||
图片预览






文档简介
(共27张PPT)
第六单元 圆
第24课时 圆的基本性质
(每年必考1道,3分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
中考试题中的数学文化
4
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:九下第三章P64-P88;
人教:九上第二十四章P79-P91、P105-P110.
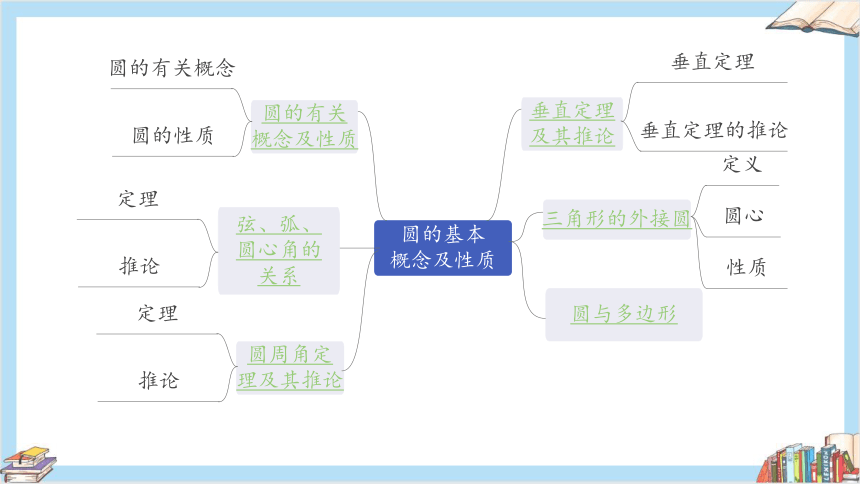
圆的基本
概念及性质
圆的有关
概念及性质
圆的有关概念
圆的性质
弦、弧、
圆心角的
关系
定理
推论
圆周角定
理及其推论
定理
推论
垂直定理
及其推论
垂直定理
垂直定理的推论
三角形的外接圆
定义
圆心
性质
圆与多边形
圆的有关概念及性质
考点
1
1. 定义:平面上到定点的距离等于定长的所有点组成的图形叫做圆.其中定点称为______,定长称为半径.如图,以点O为圆心的圆记作⊙O,线段OA叫做半径.
2. 确定圆的条件:
(1)圆心确定圆的位置,________确定圆的大小;
(2)不在同一条直线上的三个点确定一个圆.
圆心
半径
返回思维导图
3. 圆的有关概念:
(1)弦:连接圆上任意两点的________叫做弦,如AC、BC;
(2)直径:经过________的弦叫做直径,直径等于半径的2倍;
(3)弧:圆上任意两点间的部分叫做圆弧,简称弧,大于半圆的弧叫做______,如 ,小于半圆的弧叫做______,如 、 、 ;
(4)圆周角:顶点在圆上,并且两边都与圆相交的角叫做圆周角,如∠ACB;
(5)圆心角:顶点在________的角叫做圆心角,如∠AOB;
(6)弦心距:圆心到弦的距离叫做弦心距,如OD.
4. 圆的对称性:圆既是轴对称图形又是中心对称图形,对称轴是任意一条____ 所在的直线,对称中心是________.
线段
圆心
优弧
劣弧
圆心
直径
圆心
返回思维导图
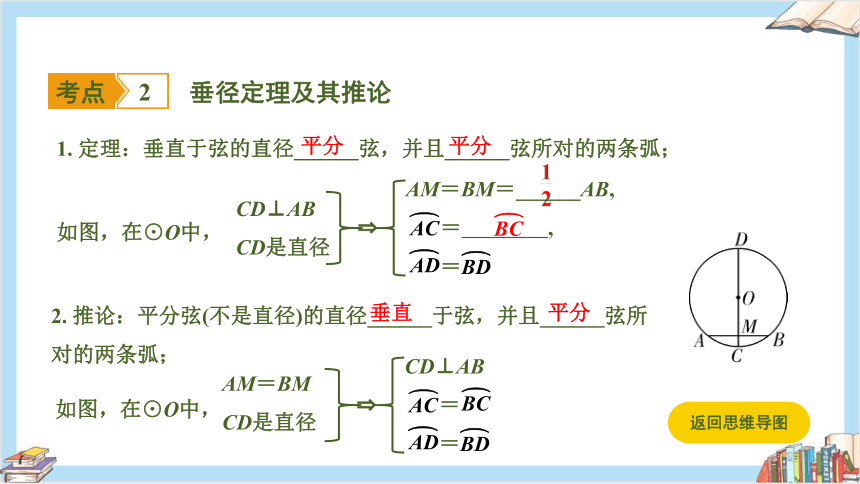
垂径定理及其推论
考点
2
1. 定理:垂直于弦的直径______弦,并且______弦所对的两条弧;
如图,在⊙O中,
CD⊥AB
CD是直径
AM=BM=______AB,
= ,
=
2. 推论:平分弦(不是直径)的直径______于弦,并且______弦所对的两条弧;
如图,在⊙O中,
AM=BM
CD是直径
CD⊥AB
=
=
平分
平分
垂直
平分
返回思维导图
【提分要点】垂径定理及其推论的延伸:根据圆的对称性,在以下五个结论中:① = ;② = ;③AM=BM;④AB⊥CD;⑤CD是直径,只要满足其中两个结论,另外三个结论一定成立,即“知二推三”.
返回思维导图
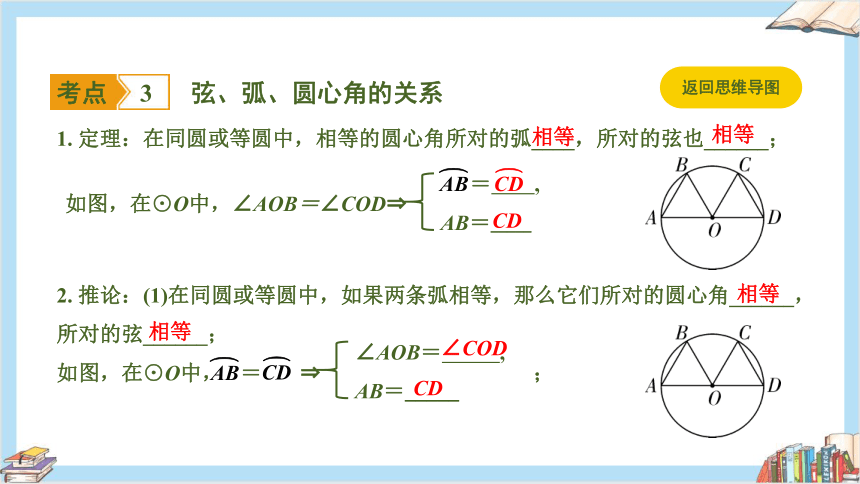
弦、弧、圆心角的关系
考点
3
1. 定理:在同圆或等圆中,相等的圆心角所对的弧____,所对的弦也______;
如图,在⊙O中,∠AOB=∠COD
= ,
AB=_____
2. 推论:(1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角______,所对的弦______;
如图,在⊙O中, = ;
∠AOB= ,
AB=_____
相等
相等
CD
相等
相等
∠COD
CD
返回思维导图
(2)在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角______,所对的优弧与劣弧分别______;
AB=CD
∠AOB= ,
=______
【提分要点】(1)理解圆心角、弧、弦三者之间的关系时,注意一条弦对着两条弧,一条弧对应无数个圆周角.(2)在同圆或等圆中,两个圆心角、两条弦、两条弧中如果有一组量相等,则它们所对应的其余各组量也相等.
相等
相等
∠COD
返回思维导图
圆周角定理及其推论
考点
4
1. 定理
内容 一条弧所对的圆周角等于它所对的圆心角的______ 常见图形
结论 ∠APB=______ 一半
返回思维导图
2. 推论
(1)同弧或等弧所对的圆周角____;如图,在⊙O中,∠A和____是 所对的圆周角 ∠A=____; = ∠A=______;
(2)半圆(或直径)所对的圆周角是___________,90°的圆周角所对的弦是______;如图,在⊙O中,AB是直径 ∠ACB=______.
【提分要点】在遇到与直径有关的问题时,一般要构造直径所对的圆周角,由直径转化出直角.
相等
∠D
∠D
∠BCD
直角(或90°)
直径
90°
返回思维导图
三角形的外接圆
考点
5
1. 定义:经过三角形的三个顶点形成的圆.
2. 圆心:外心(三角形外接圆的圆心或三角形 __________________的交点).
3. 性质:三角形的外心到三角形__________的距离相等.
三边垂直平分线
三个顶点
返回思维导图
圆与多边形
考点
6
1. 圆内接四边形的概念:如图,四边形ABCD的所有顶点都在同一个圆上,这个四边形叫做圆内接四边形.
2. 圆内接四边形的性质:(如图)
(1)圆内接四边形的对角______,如∠A+∠BCD=_____,∠B+∠D=_____;
(2)圆内接四边形的任意一个角的外角等于它的______,如∠DCE=______.
互补
180°
180°
内对角
∠A
返回思维导图
3. 圆与正多边形
如图,设正n边形的边长为a,则边心距r= ;正n边形的周长L=na;正n边形的面积S= Lr= nar;中心角θ= .
返回思维导图
回归教材
题图
证明:圆内接四边形对角互补.
已知:如图,四边形ABCD为⊙O的内接四边形.
求证:∠B+∠D=180°.
【自主解答】
解图①
证明:
证法一:如解图①,连接AO、CO,由圆周角定理得:
证法二:
如解图②,连接CA、BD,
∵∠1=∠2,∠3=∠4,
∴∠ADC=∠1+∠3=∠2+∠4,
∴∠ADC+∠ABC=∠2+∠4+∠ABC=180°.
解图②
典例“串”考点
例题图
例 如图,在⊙O中,AB为⊙O的直径,点C为⊙O上异于A,B的点.
(1)如图①,∠ACB=________°.
(2)如图①,连接OC,若∠COB=110°,则∠CAB=____°.
(3)如图②,点D为⊙O上异于A、B、C的一点,且位于AB上方,连接AD、BD、CD,并延长BD至点E,若∠ABC=30°.
①∠CDE=________°;
②连接OC,OD,若AC=BD,则∠COD=________°;
90
55
60
60
③若点C是弧 的中点,连接OC交AD于点F,AD=8,则∠CAD=________°,⊙O的半径为________.
(4)如图③,点D为⊙O上异于A、B、C的一点,且位于AB下方,连接BD、CD.
①若∠CAB=50°,CD=BD,则∠ABD=______°;
②若AB⊥CD于点E,CD=8,AE=2,则⊙O的半径为______;
③若点D为弧 的中点,连接OD,cos∠ABC= ,AC=6,则BD的长为______,CD的长为______.
30
25
5
陕西5年真题、副题“明”考法
垂径定理及圆周角定理的相关(5年4考)
命题点
1
第1题图
类型一 圆周角定理的相关计算(5年2考)
1. (2021陕西9题3分)如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为( )
A. 15° B. 35° C. 25° D. 45°
A
第2题图
2. (2021襄阳9题3分)如图,AB是⊙O的直径,EF、EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF.若∠AOF=40°,则∠F的度数是( )
A. 20° B. 35° C. 40° D. 55°
第3题图
3. (2021南阳副题9题3分)如图,矩形ABCD内接于⊙O,点P是 上一点,连接PB、PC.若AD=2AB,则sin∠BPC的值为( )
A. B. C. D.
B
B
类型二 垂径定理与圆周角定理结合的相关计算(5年2考)
4. (2021福州副题9题3分)如图,在⊙O中,弦AB垂直平分半径OC,垂足为D.若点P是⊙O上异于点A、B的任意一点,则∠APB=( )
A.30°或60° B.60°或150° C.30°或150° D.60°或120°
第4题图
5. (2021厦门9题3分)如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )
A. B. C. D.
第5题图
D
B
6. (2021烟台9题3分)如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5.若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )
A. 5 B. C. D.
第6题图
7. (2019陕西副题9题3分)如图,⊙O的半径为5,△ABC内接于⊙O,且BC=8,AB=AC,点D在 上.若∠AOD=∠BAC,则CD的长为( )
A. 5 B. 6 C. 7 D. 8
第7题图
D
B
圆内接四边形
命题点
2
8. (2021烟台副题9题3分)如图,四边形ABCD是⊙O的内接四边形,AD=BC.若∠BAC=45°,∠B=75°,则下列等式成立的是( )
A. AB=2CD B. AB= CD
C. AB= CD D. AB= CD
B
第8题图
命题点
3
与圆有关的最值问题(2015.14,近4年填空题未考查此题型,但在第25题利用辅助圆解题时会涉及)
9. (2021兰州 14题3分)如图,AB是⊙O的弦,AB=6,点C是⊙O上的一个动点,且∠ACB=45°.若点M、N分别是AB、BC的中点,则MN长的最大值是____.
10. (2021陕西副题14题3分)如图,A、B是半圆O上的两点,MN是直径,OB⊥MN.若AB=4,OB=5,P是MN上的一动点,则PA+PB的最小值为_____.
第9题图
第10题图
点击链接至练习册
第六单元 圆
第24课时 圆的基本性质
(每年必考1道,3分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
中考试题中的数学文化
4
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:九下第三章P64-P88;
人教:九上第二十四章P79-P91、P105-P110.
圆的基本
概念及性质
圆的有关
概念及性质
圆的有关概念
圆的性质
弦、弧、
圆心角的
关系
定理
推论
圆周角定
理及其推论
定理
推论
垂直定理
及其推论
垂直定理
垂直定理的推论
三角形的外接圆
定义
圆心
性质
圆与多边形
圆的有关概念及性质
考点
1
1. 定义:平面上到定点的距离等于定长的所有点组成的图形叫做圆.其中定点称为______,定长称为半径.如图,以点O为圆心的圆记作⊙O,线段OA叫做半径.
2. 确定圆的条件:
(1)圆心确定圆的位置,________确定圆的大小;
(2)不在同一条直线上的三个点确定一个圆.
圆心
半径
返回思维导图
3. 圆的有关概念:
(1)弦:连接圆上任意两点的________叫做弦,如AC、BC;
(2)直径:经过________的弦叫做直径,直径等于半径的2倍;
(3)弧:圆上任意两点间的部分叫做圆弧,简称弧,大于半圆的弧叫做______,如 ,小于半圆的弧叫做______,如 、 、 ;
(4)圆周角:顶点在圆上,并且两边都与圆相交的角叫做圆周角,如∠ACB;
(5)圆心角:顶点在________的角叫做圆心角,如∠AOB;
(6)弦心距:圆心到弦的距离叫做弦心距,如OD.
4. 圆的对称性:圆既是轴对称图形又是中心对称图形,对称轴是任意一条____ 所在的直线,对称中心是________.
线段
圆心
优弧
劣弧
圆心
直径
圆心
返回思维导图
垂径定理及其推论
考点
2
1. 定理:垂直于弦的直径______弦,并且______弦所对的两条弧;
如图,在⊙O中,
CD⊥AB
CD是直径
AM=BM=______AB,
= ,
=
2. 推论:平分弦(不是直径)的直径______于弦,并且______弦所对的两条弧;
如图,在⊙O中,
AM=BM
CD是直径
CD⊥AB
=
=
平分
平分
垂直
平分
返回思维导图
【提分要点】垂径定理及其推论的延伸:根据圆的对称性,在以下五个结论中:① = ;② = ;③AM=BM;④AB⊥CD;⑤CD是直径,只要满足其中两个结论,另外三个结论一定成立,即“知二推三”.
返回思维导图
弦、弧、圆心角的关系
考点
3
1. 定理:在同圆或等圆中,相等的圆心角所对的弧____,所对的弦也______;
如图,在⊙O中,∠AOB=∠COD
= ,
AB=_____
2. 推论:(1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角______,所对的弦______;
如图,在⊙O中, = ;
∠AOB= ,
AB=_____
相等
相等
CD
相等
相等
∠COD
CD
返回思维导图
(2)在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角______,所对的优弧与劣弧分别______;
AB=CD
∠AOB= ,
=______
【提分要点】(1)理解圆心角、弧、弦三者之间的关系时,注意一条弦对着两条弧,一条弧对应无数个圆周角.(2)在同圆或等圆中,两个圆心角、两条弦、两条弧中如果有一组量相等,则它们所对应的其余各组量也相等.
相等
相等
∠COD
返回思维导图
圆周角定理及其推论
考点
4
1. 定理
内容 一条弧所对的圆周角等于它所对的圆心角的______ 常见图形
结论 ∠APB=______ 一半
返回思维导图
2. 推论
(1)同弧或等弧所对的圆周角____;如图,在⊙O中,∠A和____是 所对的圆周角 ∠A=____; = ∠A=______;
(2)半圆(或直径)所对的圆周角是___________,90°的圆周角所对的弦是______;如图,在⊙O中,AB是直径 ∠ACB=______.
【提分要点】在遇到与直径有关的问题时,一般要构造直径所对的圆周角,由直径转化出直角.
相等
∠D
∠D
∠BCD
直角(或90°)
直径
90°
返回思维导图
三角形的外接圆
考点
5
1. 定义:经过三角形的三个顶点形成的圆.
2. 圆心:外心(三角形外接圆的圆心或三角形 __________________的交点).
3. 性质:三角形的外心到三角形__________的距离相等.
三边垂直平分线
三个顶点
返回思维导图
圆与多边形
考点
6
1. 圆内接四边形的概念:如图,四边形ABCD的所有顶点都在同一个圆上,这个四边形叫做圆内接四边形.
2. 圆内接四边形的性质:(如图)
(1)圆内接四边形的对角______,如∠A+∠BCD=_____,∠B+∠D=_____;
(2)圆内接四边形的任意一个角的外角等于它的______,如∠DCE=______.
互补
180°
180°
内对角
∠A
返回思维导图
3. 圆与正多边形
如图,设正n边形的边长为a,则边心距r= ;正n边形的周长L=na;正n边形的面积S= Lr= nar;中心角θ= .
返回思维导图
回归教材
题图
证明:圆内接四边形对角互补.
已知:如图,四边形ABCD为⊙O的内接四边形.
求证:∠B+∠D=180°.
【自主解答】
解图①
证明:
证法一:如解图①,连接AO、CO,由圆周角定理得:
证法二:
如解图②,连接CA、BD,
∵∠1=∠2,∠3=∠4,
∴∠ADC=∠1+∠3=∠2+∠4,
∴∠ADC+∠ABC=∠2+∠4+∠ABC=180°.
解图②
典例“串”考点
例题图
例 如图,在⊙O中,AB为⊙O的直径,点C为⊙O上异于A,B的点.
(1)如图①,∠ACB=________°.
(2)如图①,连接OC,若∠COB=110°,则∠CAB=____°.
(3)如图②,点D为⊙O上异于A、B、C的一点,且位于AB上方,连接AD、BD、CD,并延长BD至点E,若∠ABC=30°.
①∠CDE=________°;
②连接OC,OD,若AC=BD,则∠COD=________°;
90
55
60
60
③若点C是弧 的中点,连接OC交AD于点F,AD=8,则∠CAD=________°,⊙O的半径为________.
(4)如图③,点D为⊙O上异于A、B、C的一点,且位于AB下方,连接BD、CD.
①若∠CAB=50°,CD=BD,则∠ABD=______°;
②若AB⊥CD于点E,CD=8,AE=2,则⊙O的半径为______;
③若点D为弧 的中点,连接OD,cos∠ABC= ,AC=6,则BD的长为______,CD的长为______.
30
25
5
陕西5年真题、副题“明”考法
垂径定理及圆周角定理的相关(5年4考)
命题点
1
第1题图
类型一 圆周角定理的相关计算(5年2考)
1. (2021陕西9题3分)如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为( )
A. 15° B. 35° C. 25° D. 45°
A
第2题图
2. (2021襄阳9题3分)如图,AB是⊙O的直径,EF、EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF.若∠AOF=40°,则∠F的度数是( )
A. 20° B. 35° C. 40° D. 55°
第3题图
3. (2021南阳副题9题3分)如图,矩形ABCD内接于⊙O,点P是 上一点,连接PB、PC.若AD=2AB,则sin∠BPC的值为( )
A. B. C. D.
B
B
类型二 垂径定理与圆周角定理结合的相关计算(5年2考)
4. (2021福州副题9题3分)如图,在⊙O中,弦AB垂直平分半径OC,垂足为D.若点P是⊙O上异于点A、B的任意一点,则∠APB=( )
A.30°或60° B.60°或150° C.30°或150° D.60°或120°
第4题图
5. (2021厦门9题3分)如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )
A. B. C. D.
第5题图
D
B
6. (2021烟台9题3分)如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5.若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )
A. 5 B. C. D.
第6题图
7. (2019陕西副题9题3分)如图,⊙O的半径为5,△ABC内接于⊙O,且BC=8,AB=AC,点D在 上.若∠AOD=∠BAC,则CD的长为( )
A. 5 B. 6 C. 7 D. 8
第7题图
D
B
圆内接四边形
命题点
2
8. (2021烟台副题9题3分)如图,四边形ABCD是⊙O的内接四边形,AD=BC.若∠BAC=45°,∠B=75°,则下列等式成立的是( )
A. AB=2CD B. AB= CD
C. AB= CD D. AB= CD
B
第8题图
命题点
3
与圆有关的最值问题(2015.14,近4年填空题未考查此题型,但在第25题利用辅助圆解题时会涉及)
9. (2021兰州 14题3分)如图,AB是⊙O的弦,AB=6,点C是⊙O上的一个动点,且∠ACB=45°.若点M、N分别是AB、BC的中点,则MN长的最大值是____.
10. (2021陕西副题14题3分)如图,A、B是半圆O上的两点,MN是直径,OB⊥MN.若AB=4,OB=5,P是MN上的一动点,则PA+PB的最小值为_____.
第9题图
第10题图
点击链接至练习册
同课章节目录
