【中考数学总复习】第30课时 统 计 课件
文档属性
| 名称 | 【中考数学总复习】第30课时 统 计 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 14:50:29 | ||
图片预览











文档简介
(共31张PPT)
第八单元 统计与概率
第30课时 统 计
(每年必考1道,2018年开始调整在第19题考查,5或7分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:七上第六章P154-P188,八上第六章P135-P160;
人教:七下第十章P134-P161,八下第二十章P110-P137.
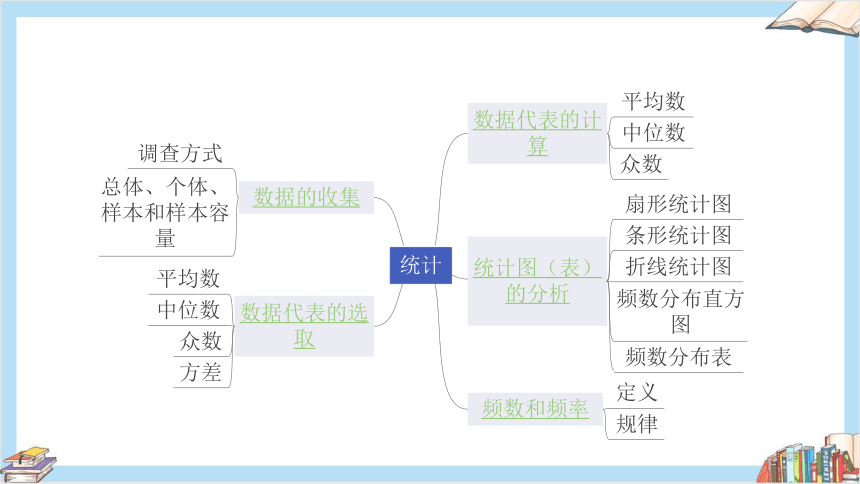
统计
数据的收集
调查方式
总体、个体、样本和样本容量
数据代表的计算
平均数
中位数
众数
平均数
数据代表的选取
中位数
众数
方差
统计图(表)的分析
扇形统计图
条形统计图
折线统计图
频数分布直方图
频数分布表
定义
频数和频率
规律
数据的收集
考点
1
1. 调查方式
(1)全面调查
定义:考察全体对象的调查,也称普查.
①测量某班学生的身高;(调查范围小)
②乘飞机前对乘客的安检;(意义重大)
③对嫦娥五号飞船上各种零部件质量情况的检查;(意义重大)
④人口普查.(数据要求准确)
总结:一般当调查的范围小、调查不具有破坏性、意义重大、数据要求准确、全面时,采用全面调查.
返回思维导图
(2)抽样调查
定义:抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况.
①调查全国中小学生课外阅读情况;(人数多,范围广)
②调查某市中学生的视力情况;(人数多)
③对70周年大阅兵收视率的调查;(人数多)
④检查一批手机电池的使用寿命.(具有破坏性)
总结:一般当所调查对象涉及面广、范围大、受条件限制或具有破坏性时,采用抽样调查.
返回思维导图
2. 总体、个体、样本和样本容量
某中学初三800名学生参加了中考体育测试,为了解这些学生的体考成绩,现从中抽取80名学生的体考成绩进行分析,则在这次调查中,
总体(在统计中所考查对象的全体):___________________________;
个体(组成总体的每个对象):_________________________________;
样本(从总体中抽取的一部分个体):____________________________;
样本容量(样本中个体的数量):___________________.
800名初三学生的体考成绩
每名初三学生的体考成绩
80名初三学生的体考成绩
80
返回思维导图
数据代表的计算
考点
2
1. 平均数
(1)算术平均数
对于n个数x1,x2,…,xn,其(算术)平均数x=________________.
(2)加权平均数
当所给的一组数据中存在一些数据出现的次数大于1,则该组数据的平均数叫加权平均数.
x=______________________,其中f1,f2,…,fk分别表示x1,x2,…,xk出现的次数,n=f1+f2+…+fk.
返回思维导图
2. 中位数
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数据为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
3. 众数
一组数据中出现次数最多的数据称为这组数据的众数.
【提分要点】1. 一组数据中,平均数、中位数都是唯一的,众数可以有多个,也可以没有;
2. 如果有两个或两个以上的数据出现次数都是最多的,那么这几个数据都是这组数据的众数;如果所有数据出现的次数都一样,那么这组数据没有众数.
返回思维导图
4. 方差
若n个数据x1,x2,…,xn的平均数是x,则方差:s2= ×[(x1-x)2+(x2-x)2+…+(xn-x)2]
返回思维导图
数据代表的选取
考点
3
1. 平均数
特点:唯一能反映一组数据的平均水平,与数据的排列位置无关,容易受最大或最小这两个数据的影响;
适用情况:求某班期末考试数学成绩的平均成绩、歌唱比赛去掉最高分和最低分求平均得分等.
2. 中位数
特点:通过数据排序得到,故不受最大或最小这两个数据的影响;
适用情况:根据比赛成绩的中位数,确定某人的成绩是否在全部参赛人员的前50%,去掉一组数据的一个最大值和一个最小值,中位数不变等.
返回思维导图
3. 众数
特点:表示一组数据中出现次数最多的数据,次数多能够反映一组数据的集中程度;
适用情况:日常生活中“最佳”“最受欢迎”“最满意”“最受关注”等,都与众数有关,它反映的是一组数据的集中程度.
4. 方差
特点:方差越大,数据的波动越大,稳定性越差;方差越小,数据的波动越小,稳定性越好.反之也成立;
适用情况:在平均成绩相同的情况下,比较两个人状态的稳定性.(被调查的每个数据同时加上(或减去)同一个数值,该组数据的方差不变)
返回思维导图
统计图(表)的分析
考点
4
名称 优点 图中所含信息
扇形统计图 能清楚地表示出各部分在总体中所占的百分比 1. 各百分比之和等于12. 圆心角的度数=百分比×360°
条形统计图 能清楚地表示出每个项目的具体数目 各组数量之和等于抽样数据总数(样本容量)
折线统计图 能清楚地反映数据的变化情况 各组数据之和等于抽样数据总数(样本容量)
返回思维导图
名称 优点 图中所含信息
频数分布直方图 能清楚地表示出收集或调查到的数据,能显示出各数据分布的情况以及各组频数之间的差别 各组频数之和等于抽样数据总数(样本容量)
频数分布表 能清楚地表示出各部分在总体中所占的百分比,能清楚地表示出每个项目的具体数目 1. 各组频率之和等于1
2. 数据总数×某组的频率=相应组的频数
返回思维导图
频数和频率
考点
5
频数 频率
定义 统计时,落在各小组的数据________ 每个小组的________与数据总数的比值
规律 各小组的频数之和等于数据________ 各小组的频率之和等于________
个数
频数
总数
1
返回思维导图
典例“串”考点
例 某市正在努力创建“全国文明城市”,为进一步营造 “创文”氛围,某学校组织了一次“创文知识竞赛”,竞 赛题满分 10分.竞赛活动结束后,学校团委随机抽查 20名考生的考卷,对考生答题得分情况进行统计,发 现所抽取的考 卷 中 得 分 最 少 为 6分,且 统 计 数 据 如下:
数据收集:
7 8 6 8 10 9 8 7 10 9
9 8 10 9 7 8 6 10 9 9
数据整理:
“创文知识竞赛”学生答题得分统计表
得分分值(分) 画正计数 人数(频数)
6 ________
7 ________
8 ______ ________
9 ______ ________
10 ______ ________
“创文知识竞赛”学生答题得分统计图
A-6分
B-7分
C-8分
D-9分
E-10分
例题图
2
3
正
5
6
4
请根据以上统计信息,解答下列问题:
(1)本次抽查的样本容量是________;
(2)在扇形统计图中,m=________,n=________;
(3)在扇形统计图中,“D-9分”所对圆心角的度数为________;
(4)补全条形统计图;
(5)本次所抽取考卷中答题得分的众数为______分,中位数为________分;
(6)求本次所抽取考卷中答题得分的平均数;
(7)参与调查的小明同学说“这次知识竞赛中我得了8分,排名在中等偏上!”小明的说法正确吗?请说明理由;
(8)已知该校共有2000名学生,请你估计该校学生“创文知识竞赛”答题得分为10分的人数.
20
15
30
108°
例题解图
9
8.5
(6)本次所抽取考卷中答题得分的平均数为 ×(2×6+3×7+5×8+6×9+10×4)=8.35;
(7)不正确.理由:本次所抽取考卷中答题得分分值的中位数是8.5,
∵8<8.5,
∴小明的排名在中等偏下;
(8)2000× =400(人),
答:该校学生中“创文知识竞赛”答题得分为10分的人数约为400人.
陕西5年真题、副题“明”考法
命题点
统计图(表)的分析(必考)
1. (2017陕西18题5分)养成良好的早锻炼习惯,对学生的学习和生活都非常有益.某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间x(分钟)进行了调查.现把调查结果分成A、B、C、D四组,如表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
组别 时间x(分钟)
A 0≤x<10
B 10≤x<20
C 20≤x<30
D 30≤x<40
第1题图
请你根据以上提供的信息,解答下列问题:
(1)补全频数分布直方图和扇形统计图;
(2)所抽取的七年级学生早锻炼时间的中位数落在________区间内;
(3)已知该校七年级共有1200名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.(早锻炼:指学生在早晨7:00~7:40之间的锻炼)
解:(1)补全频数分布直方图和扇形统计图如解图;(2分)
(2)20≤x<30(或填C);(3分)
(3)1200×(65%+20%)=1020(人),
答:该校七年级学生中约有1020人一天早锻炼的时间不少于20分钟.(5分)
第1题解图
2. (2021陕西19题7分)本学期初,某校为迎接中华人民共和国建国七十周年,开展了以“不忘初心,缅怀革命先烈,奋斗新时代”为主题的读书活动.校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”(下面简称:“读书量”)进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,如下图所示:
所抽取该校七年级学生四月份“读书量”的统计图
第2题图
根据以上信息,解答下列问题:
(1)补全上面两幅统计图;填出本次所抽取学生四月份“读书量”的众数为______;
(2)求本次所抽取学生四月份“读书量”的平均数;
(3)已知该校七年级有1200名学生,请你估计该校七年级学生中,四月份“读书量”为5本的学生人数.
3本
第2题解图
(2)∵18÷30%=60(人),
∴x= ×(1×3+2×18+3×21+4×12+5×6)=3(本).
答:本次所抽取学生四月份“读书量”的平均数为3本;(5分)
(3)1200×10%=120(人),
答:估计该校七年级学生中,四月份“读书量”为5 本的学生有120人.(7分)
3. (2021洛阳副题19题7分)今年植树节,某校开展了“植树造林,从我做起”的植树活动.该校参加本次植树活动的全体学生被分成了115个植树小组,按学校要求,每个植树小组至少植树10棵.经过一天的植树活动,校团委为了了解本次植树任务的完成情况,从这115个植树小组中随机抽查了10个小组,并对这10个小组植树的棵数进行了统计,结果如下:
第3题图
根据以上提供的信息,解答下列问题:
(1)求所统计的这组数据的中位数和平均数;
(2)求抽查的这10个小组中,完成本次植树任务的小组所占的百分比;
(3)请你估计在本次植树活动中,该校学生共植树多少棵.
解:(1)∵ =10.5(棵); x= =10.6(棵).
∴所统计的这组数据的中位数为10.5棵,平均数为10.6棵;(3分)
(2)∵ ×100%=90%.
∴在抽查的10个小组中,90%的小组完成了植树任务.(5分)
(3)∵10.6×115=1219(棵).
∴估计在本次植树活动中,该校学生共植树1219棵.(7分)
4. (2021襄阳19题7分)对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,他们将全部测试成绩分成A、B、C、D四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计图表
组别 分数/分 频数 各组总分/分
A 60B 70C 80D 90第4题图
依据以上统计信息,解答下列问题:
(1)求得m=________,n=________;
(2)这次测试成绩的中位数落在____________组;
(3)求本次全部测试成绩的平均数.
30
19%
B(或70本次全部测试成绩的平均数为
答:本次全部测试成绩的平均数是80.1分.
点击链接至练习册
第八单元 统计与概率
第30课时 统 计
(每年必考1道,2018年开始调整在第19题考查,5或7分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:七上第六章P154-P188,八上第六章P135-P160;
人教:七下第十章P134-P161,八下第二十章P110-P137.
统计
数据的收集
调查方式
总体、个体、样本和样本容量
数据代表的计算
平均数
中位数
众数
平均数
数据代表的选取
中位数
众数
方差
统计图(表)的分析
扇形统计图
条形统计图
折线统计图
频数分布直方图
频数分布表
定义
频数和频率
规律
数据的收集
考点
1
1. 调查方式
(1)全面调查
定义:考察全体对象的调查,也称普查.
①测量某班学生的身高;(调查范围小)
②乘飞机前对乘客的安检;(意义重大)
③对嫦娥五号飞船上各种零部件质量情况的检查;(意义重大)
④人口普查.(数据要求准确)
总结:一般当调查的范围小、调查不具有破坏性、意义重大、数据要求准确、全面时,采用全面调查.
返回思维导图
(2)抽样调查
定义:抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况.
①调查全国中小学生课外阅读情况;(人数多,范围广)
②调查某市中学生的视力情况;(人数多)
③对70周年大阅兵收视率的调查;(人数多)
④检查一批手机电池的使用寿命.(具有破坏性)
总结:一般当所调查对象涉及面广、范围大、受条件限制或具有破坏性时,采用抽样调查.
返回思维导图
2. 总体、个体、样本和样本容量
某中学初三800名学生参加了中考体育测试,为了解这些学生的体考成绩,现从中抽取80名学生的体考成绩进行分析,则在这次调查中,
总体(在统计中所考查对象的全体):___________________________;
个体(组成总体的每个对象):_________________________________;
样本(从总体中抽取的一部分个体):____________________________;
样本容量(样本中个体的数量):___________________.
800名初三学生的体考成绩
每名初三学生的体考成绩
80名初三学生的体考成绩
80
返回思维导图
数据代表的计算
考点
2
1. 平均数
(1)算术平均数
对于n个数x1,x2,…,xn,其(算术)平均数x=________________.
(2)加权平均数
当所给的一组数据中存在一些数据出现的次数大于1,则该组数据的平均数叫加权平均数.
x=______________________,其中f1,f2,…,fk分别表示x1,x2,…,xk出现的次数,n=f1+f2+…+fk.
返回思维导图
2. 中位数
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数据为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
3. 众数
一组数据中出现次数最多的数据称为这组数据的众数.
【提分要点】1. 一组数据中,平均数、中位数都是唯一的,众数可以有多个,也可以没有;
2. 如果有两个或两个以上的数据出现次数都是最多的,那么这几个数据都是这组数据的众数;如果所有数据出现的次数都一样,那么这组数据没有众数.
返回思维导图
4. 方差
若n个数据x1,x2,…,xn的平均数是x,则方差:s2= ×[(x1-x)2+(x2-x)2+…+(xn-x)2]
返回思维导图
数据代表的选取
考点
3
1. 平均数
特点:唯一能反映一组数据的平均水平,与数据的排列位置无关,容易受最大或最小这两个数据的影响;
适用情况:求某班期末考试数学成绩的平均成绩、歌唱比赛去掉最高分和最低分求平均得分等.
2. 中位数
特点:通过数据排序得到,故不受最大或最小这两个数据的影响;
适用情况:根据比赛成绩的中位数,确定某人的成绩是否在全部参赛人员的前50%,去掉一组数据的一个最大值和一个最小值,中位数不变等.
返回思维导图
3. 众数
特点:表示一组数据中出现次数最多的数据,次数多能够反映一组数据的集中程度;
适用情况:日常生活中“最佳”“最受欢迎”“最满意”“最受关注”等,都与众数有关,它反映的是一组数据的集中程度.
4. 方差
特点:方差越大,数据的波动越大,稳定性越差;方差越小,数据的波动越小,稳定性越好.反之也成立;
适用情况:在平均成绩相同的情况下,比较两个人状态的稳定性.(被调查的每个数据同时加上(或减去)同一个数值,该组数据的方差不变)
返回思维导图
统计图(表)的分析
考点
4
名称 优点 图中所含信息
扇形统计图 能清楚地表示出各部分在总体中所占的百分比 1. 各百分比之和等于12. 圆心角的度数=百分比×360°
条形统计图 能清楚地表示出每个项目的具体数目 各组数量之和等于抽样数据总数(样本容量)
折线统计图 能清楚地反映数据的变化情况 各组数据之和等于抽样数据总数(样本容量)
返回思维导图
名称 优点 图中所含信息
频数分布直方图 能清楚地表示出收集或调查到的数据,能显示出各数据分布的情况以及各组频数之间的差别 各组频数之和等于抽样数据总数(样本容量)
频数分布表 能清楚地表示出各部分在总体中所占的百分比,能清楚地表示出每个项目的具体数目 1. 各组频率之和等于1
2. 数据总数×某组的频率=相应组的频数
返回思维导图
频数和频率
考点
5
频数 频率
定义 统计时,落在各小组的数据________ 每个小组的________与数据总数的比值
规律 各小组的频数之和等于数据________ 各小组的频率之和等于________
个数
频数
总数
1
返回思维导图
典例“串”考点
例 某市正在努力创建“全国文明城市”,为进一步营造 “创文”氛围,某学校组织了一次“创文知识竞赛”,竞 赛题满分 10分.竞赛活动结束后,学校团委随机抽查 20名考生的考卷,对考生答题得分情况进行统计,发 现所抽取的考 卷 中 得 分 最 少 为 6分,且 统 计 数 据 如下:
数据收集:
7 8 6 8 10 9 8 7 10 9
9 8 10 9 7 8 6 10 9 9
数据整理:
“创文知识竞赛”学生答题得分统计表
得分分值(分) 画正计数 人数(频数)
6 ________
7 ________
8 ______ ________
9 ______ ________
10 ______ ________
“创文知识竞赛”学生答题得分统计图
A-6分
B-7分
C-8分
D-9分
E-10分
例题图
2
3
正
5
6
4
请根据以上统计信息,解答下列问题:
(1)本次抽查的样本容量是________;
(2)在扇形统计图中,m=________,n=________;
(3)在扇形统计图中,“D-9分”所对圆心角的度数为________;
(4)补全条形统计图;
(5)本次所抽取考卷中答题得分的众数为______分,中位数为________分;
(6)求本次所抽取考卷中答题得分的平均数;
(7)参与调查的小明同学说“这次知识竞赛中我得了8分,排名在中等偏上!”小明的说法正确吗?请说明理由;
(8)已知该校共有2000名学生,请你估计该校学生“创文知识竞赛”答题得分为10分的人数.
20
15
30
108°
例题解图
9
8.5
(6)本次所抽取考卷中答题得分的平均数为 ×(2×6+3×7+5×8+6×9+10×4)=8.35;
(7)不正确.理由:本次所抽取考卷中答题得分分值的中位数是8.5,
∵8<8.5,
∴小明的排名在中等偏下;
(8)2000× =400(人),
答:该校学生中“创文知识竞赛”答题得分为10分的人数约为400人.
陕西5年真题、副题“明”考法
命题点
统计图(表)的分析(必考)
1. (2017陕西18题5分)养成良好的早锻炼习惯,对学生的学习和生活都非常有益.某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间x(分钟)进行了调查.现把调查结果分成A、B、C、D四组,如表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
组别 时间x(分钟)
A 0≤x<10
B 10≤x<20
C 20≤x<30
D 30≤x<40
第1题图
请你根据以上提供的信息,解答下列问题:
(1)补全频数分布直方图和扇形统计图;
(2)所抽取的七年级学生早锻炼时间的中位数落在________区间内;
(3)已知该校七年级共有1200名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.(早锻炼:指学生在早晨7:00~7:40之间的锻炼)
解:(1)补全频数分布直方图和扇形统计图如解图;(2分)
(2)20≤x<30(或填C);(3分)
(3)1200×(65%+20%)=1020(人),
答:该校七年级学生中约有1020人一天早锻炼的时间不少于20分钟.(5分)
第1题解图
2. (2021陕西19题7分)本学期初,某校为迎接中华人民共和国建国七十周年,开展了以“不忘初心,缅怀革命先烈,奋斗新时代”为主题的读书活动.校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”(下面简称:“读书量”)进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,如下图所示:
所抽取该校七年级学生四月份“读书量”的统计图
第2题图
根据以上信息,解答下列问题:
(1)补全上面两幅统计图;填出本次所抽取学生四月份“读书量”的众数为______;
(2)求本次所抽取学生四月份“读书量”的平均数;
(3)已知该校七年级有1200名学生,请你估计该校七年级学生中,四月份“读书量”为5本的学生人数.
3本
第2题解图
(2)∵18÷30%=60(人),
∴x= ×(1×3+2×18+3×21+4×12+5×6)=3(本).
答:本次所抽取学生四月份“读书量”的平均数为3本;(5分)
(3)1200×10%=120(人),
答:估计该校七年级学生中,四月份“读书量”为5 本的学生有120人.(7分)
3. (2021洛阳副题19题7分)今年植树节,某校开展了“植树造林,从我做起”的植树活动.该校参加本次植树活动的全体学生被分成了115个植树小组,按学校要求,每个植树小组至少植树10棵.经过一天的植树活动,校团委为了了解本次植树任务的完成情况,从这115个植树小组中随机抽查了10个小组,并对这10个小组植树的棵数进行了统计,结果如下:
第3题图
根据以上提供的信息,解答下列问题:
(1)求所统计的这组数据的中位数和平均数;
(2)求抽查的这10个小组中,完成本次植树任务的小组所占的百分比;
(3)请你估计在本次植树活动中,该校学生共植树多少棵.
解:(1)∵ =10.5(棵); x= =10.6(棵).
∴所统计的这组数据的中位数为10.5棵,平均数为10.6棵;(3分)
(2)∵ ×100%=90%.
∴在抽查的10个小组中,90%的小组完成了植树任务.(5分)
(3)∵10.6×115=1219(棵).
∴估计在本次植树活动中,该校学生共植树1219棵.(7分)
4. (2021襄阳19题7分)对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,他们将全部测试成绩分成A、B、C、D四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计图表
组别 分数/分 频数 各组总分/分
A 60
依据以上统计信息,解答下列问题:
(1)求得m=________,n=________;
(2)这次测试成绩的中位数落在____________组;
(3)求本次全部测试成绩的平均数.
30
19%
B(或70
答:本次全部测试成绩的平均数是80.1分.
点击链接至练习册
同课章节目录
