【中考数学总复习】第3课时 整式及因式分解 课件
文档属性
| 名称 | 【中考数学总复习】第3课时 整式及因式分解 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 14:50:29 | ||
图片预览







文档简介
(共20张PPT)
第一单元 数与式
第3课时 整式及因式分解
(5年4考,考则1道,3分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
中考试题中的数学文化
4
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:七上第三章P77-P104;七下第一章P1-P36;
八下第四章P91-P106
人教:七上第二章P53-P76;八上第十四章P94-P125
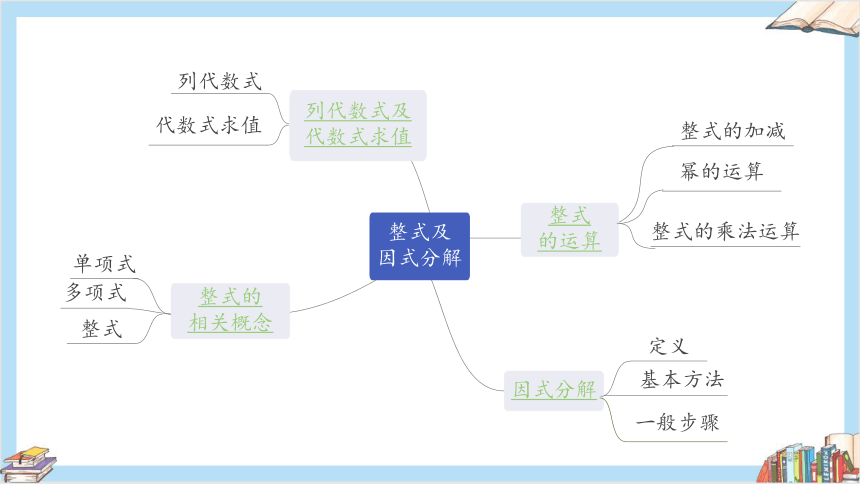
因式分解
列代数式及
代数式求值
列代数式
代数式求值
多项式
整式
整式的
相关概念
单项式
定义
一般步骤
基本方法
整式的加减
整式
的运算
幂的运算
整式的乘法运算
整式及
因式分解
列代数式及代数式求值
考点
1
1. 列代数式:
把问题中与数量有关的词语,用含有数、字母和运算符号的式子表示出来,与实际问题结合关键是找出问题中的等量关系式,如路程=速度×时间,售价=标价×折扣等.
2. 代数式求值:
直接代入法:给定字母的值,可直接将值代入式子中求解
整体代入法:当单个字母的值不能或不易求时,可把已知条件作为一个整体,代入到所求的代数式中,这种方法常要先对已知条件或者所求代数式进行变形,如找倍数关系,因式分解、配方等.
返回思维导图
整式的相关概念
考点
2
1. 单项式:由数字与字母或字母与字母的乘积所组成的代数式叫做单项式.单独一个数字或字母也是单项式;
(1)单项式的系数:单项式中的数字因数;
(2)单项式的次数:一个单项式中,所有字母的指数之和.
如
2. 多项式:几个单项式的和.
多项式中次数最高项的次数叫做多项式的次数,如2x+x2y的次数是________.
3. 整式:单项式与多项式统称为整式.
3
返回思维导图
整式的运算
考点
3
1. 整式的加减:实质是合并同类项.
(1)同类项:所含字母相同,并且相同字母的______也相同.常数项都是同类项.
(2)合并同类项:同类项的________相加减,作为结果的系数,字母与字母的________不变.
(3)去括号法则:括号前是“+”号,括号内各项不变号,
a+(b+c)= a______b______c;
括号前是“-”号,括号内每一项都变号,
a-(b+c)=a_____b______c.
指数
系数
指数
+
+
-
-
返回思维导图
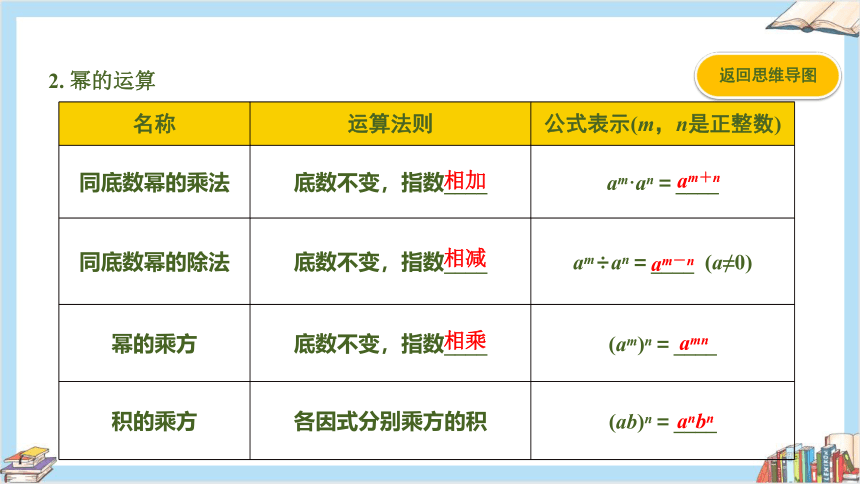
2. 幂的运算
名称 运算法则 公式表示(m,n是正整数)
同底数幂的乘法 底数不变,指数____ am·an=____
同底数幂的除法 底数不变,指数____ am÷an=____ (a≠0)
幂的乘方 底数不变,指数____ (am)n=____
积的乘方 各因式分别乘方的积 (ab)n=____
相加
am+n
相减
am-n
相乘
amn
anbn
返回思维导图
3. 整式的乘法运算
运算 法则
单项式乘单项式 (1)系数:系数与系数的________作为积的系数;(2)相同字母:同底数幂相乘作为积的一个因式;(3)单独字母:单独含有的字母连同它的指数直接作为积的一个因式
单项式乘多项式 用单项式去乘多项式的每一项,再把所得的积相加
多项式乘多项式 先用一个多项式的每一项去乘另一个多项式的每一项,再把所得的积相加
乘法公式 平方差公式:(a+b)(a-b)=________完全平方公式:(a±b)2=__________
乘积
a2-b2
a2±2ab+b2
返回思维导图
因式分解
考点
4
1. 定义:把一个多项式表示成若干个整式的积的形式.
2. 基本方法
(1)提公因式法:ma+mb+mc=__________;
(2)公式法:a2-b2
因式分解
整式乘法
_________
a2±2ab+b2
______
m(a+b+c)
(a+b)(a-b)
(a±b)2
因式分解
整式乘法
返回思维导图
3. 一般步骤
【提分要点】(1)因式分解一定要分解到每个因式都不能再分解为止;(2)能提取公因式的,首先要提取公因式,特别是有数字因式的,更不要忽略;(3)结果一定是积的形式.
返回思维导图
回归教材
用图形面积验证乘法公式
1. 如图①,边长为a的大正方形中有一个边长为b的小正方形.将图①中的阴影部分拼成如图②所示的长方形.
(1)图①中阴影部分的面积为___________,图②中阴影部分面积为 _;
(2)通过观察比较两图的阴影部分面积,可以得到乘法公式为 ___________________ .(用式子表达)
第1题图
a2-b2
(a+b)(a-b)
a2-b2=(a+b)(a-b)
2. 如图,将一个边长为a的正方形的边长增加b,形成两个正方形和两个矩形,请通过图形面积验证完全平方公式.
第2题图
【自主解答】
证明:∵边长为a的正方形边长增加b后形成的大正方形的边长为a+b,
∴其面积可以表示成(a+b)2,
又∵它由两个正方形和两个矩形构成,
∴其面积又可以表示成a2+2ab+b2,
则(a+b)2=a2+2ab+b2.
典例“串”考点
例1 下列各式中:① 2x2y3 ,② x-3y,③ - ambn,
④ 2xy-6y,⑤ 5a2bcp,⑥ 3+2x-6y,⑦-3x2+3x.
(1)其中单项式有________,多项式有__________;
(2)2x2y3的系数是________,次数是________;
(3)-3x2+3x是________次________项式;
(4)若- ambn与5a2bcp为同类项,则m=______,n=______,p=________;
(5)当x=2,y=1时,x-3y的值为______,此时3+2x-6y的值为________.
①③⑤
②④⑥⑦
2
5
二
二
2
1
0
-1
1
例2 判断下列运算的正误:
(1)x2+4x2=5x4 ( )
(2)2x-3x2=-x ( )
(3)3a2·2a3=5a5 ( )
(4)(-2a3b2)2=4a6b4 ( )
(5)12m6n2÷(-4m3n)=-3m3n ( )
(6)(a-2b)2=a2-4ab+4b2 ( )
(7)(2-a)(a+2)=a2-4 ( )
(8)(x-1)(x-2)=x2-3x-2 ( )
×
√
√
√
×
×
×
×
例3 根据题意解答下列各题:
(1)因式分解:5x2-5xy=________;
(2)因式分解:x2y-y3= _ ;
(3)因式分解:4x2+4xy+y2= ;
(4)因式分解:-x3y+6x2y-9xy= .
5x(x-y)
y(x-y)(x+y)
(2x+y)2
-xy(x-3)2
5年真题、副题“明”考法
命题点
整式的运算(5年4考)
1. 计算:(-2x2y)3=( )
A. -8x6y3 B. 8x6y3
C. -6x6y3 D. 6x5y3
2.下列计算正确的是( )
A. x2+3x2=4x4 B. x2y·2x3=2x6y
C. (6x3y2)÷(3x)=2x2 D. (-3x)2=9x2
A
D
3. 下列计算正确的是( )
A. 2a2·3a2=6a2 B. (-3a2b)2=6a4b2
C. (a-b)2=a2-b2 D. -a2+2a2=a2
4. 下列计算正确的是( )
A. 3a4-a4=3
B. (-5x3y2 )2=10x6y4
C. (x+1)(x-2)=x2-x-2
D. (ab-1)2=a2b2-1
D
C
5. 下列计算正确的是( )
A.a2+a3=a5
B.2x2·( xy)= x3y
C.(a-b)(-a-b)=a2-b2
D.(-2x2y)3=-6x6y3
B
点击链接至练习册
第一单元 数与式
第3课时 整式及因式分解
(5年4考,考则1道,3分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
中考试题中的数学文化
4
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:七上第三章P77-P104;七下第一章P1-P36;
八下第四章P91-P106
人教:七上第二章P53-P76;八上第十四章P94-P125
因式分解
列代数式及
代数式求值
列代数式
代数式求值
多项式
整式
整式的
相关概念
单项式
定义
一般步骤
基本方法
整式的加减
整式
的运算
幂的运算
整式的乘法运算
整式及
因式分解
列代数式及代数式求值
考点
1
1. 列代数式:
把问题中与数量有关的词语,用含有数、字母和运算符号的式子表示出来,与实际问题结合关键是找出问题中的等量关系式,如路程=速度×时间,售价=标价×折扣等.
2. 代数式求值:
直接代入法:给定字母的值,可直接将值代入式子中求解
整体代入法:当单个字母的值不能或不易求时,可把已知条件作为一个整体,代入到所求的代数式中,这种方法常要先对已知条件或者所求代数式进行变形,如找倍数关系,因式分解、配方等.
返回思维导图
整式的相关概念
考点
2
1. 单项式:由数字与字母或字母与字母的乘积所组成的代数式叫做单项式.单独一个数字或字母也是单项式;
(1)单项式的系数:单项式中的数字因数;
(2)单项式的次数:一个单项式中,所有字母的指数之和.
如
2. 多项式:几个单项式的和.
多项式中次数最高项的次数叫做多项式的次数,如2x+x2y的次数是________.
3. 整式:单项式与多项式统称为整式.
3
返回思维导图
整式的运算
考点
3
1. 整式的加减:实质是合并同类项.
(1)同类项:所含字母相同,并且相同字母的______也相同.常数项都是同类项.
(2)合并同类项:同类项的________相加减,作为结果的系数,字母与字母的________不变.
(3)去括号法则:括号前是“+”号,括号内各项不变号,
a+(b+c)= a______b______c;
括号前是“-”号,括号内每一项都变号,
a-(b+c)=a_____b______c.
指数
系数
指数
+
+
-
-
返回思维导图
2. 幂的运算
名称 运算法则 公式表示(m,n是正整数)
同底数幂的乘法 底数不变,指数____ am·an=____
同底数幂的除法 底数不变,指数____ am÷an=____ (a≠0)
幂的乘方 底数不变,指数____ (am)n=____
积的乘方 各因式分别乘方的积 (ab)n=____
相加
am+n
相减
am-n
相乘
amn
anbn
返回思维导图
3. 整式的乘法运算
运算 法则
单项式乘单项式 (1)系数:系数与系数的________作为积的系数;(2)相同字母:同底数幂相乘作为积的一个因式;(3)单独字母:单独含有的字母连同它的指数直接作为积的一个因式
单项式乘多项式 用单项式去乘多项式的每一项,再把所得的积相加
多项式乘多项式 先用一个多项式的每一项去乘另一个多项式的每一项,再把所得的积相加
乘法公式 平方差公式:(a+b)(a-b)=________完全平方公式:(a±b)2=__________
乘积
a2-b2
a2±2ab+b2
返回思维导图
因式分解
考点
4
1. 定义:把一个多项式表示成若干个整式的积的形式.
2. 基本方法
(1)提公因式法:ma+mb+mc=__________;
(2)公式法:a2-b2
因式分解
整式乘法
_________
a2±2ab+b2
______
m(a+b+c)
(a+b)(a-b)
(a±b)2
因式分解
整式乘法
返回思维导图
3. 一般步骤
【提分要点】(1)因式分解一定要分解到每个因式都不能再分解为止;(2)能提取公因式的,首先要提取公因式,特别是有数字因式的,更不要忽略;(3)结果一定是积的形式.
返回思维导图
回归教材
用图形面积验证乘法公式
1. 如图①,边长为a的大正方形中有一个边长为b的小正方形.将图①中的阴影部分拼成如图②所示的长方形.
(1)图①中阴影部分的面积为___________,图②中阴影部分面积为 _;
(2)通过观察比较两图的阴影部分面积,可以得到乘法公式为 ___________________ .(用式子表达)
第1题图
a2-b2
(a+b)(a-b)
a2-b2=(a+b)(a-b)
2. 如图,将一个边长为a的正方形的边长增加b,形成两个正方形和两个矩形,请通过图形面积验证完全平方公式.
第2题图
【自主解答】
证明:∵边长为a的正方形边长增加b后形成的大正方形的边长为a+b,
∴其面积可以表示成(a+b)2,
又∵它由两个正方形和两个矩形构成,
∴其面积又可以表示成a2+2ab+b2,
则(a+b)2=a2+2ab+b2.
典例“串”考点
例1 下列各式中:① 2x2y3 ,② x-3y,③ - ambn,
④ 2xy-6y,⑤ 5a2bcp,⑥ 3+2x-6y,⑦-3x2+3x.
(1)其中单项式有________,多项式有__________;
(2)2x2y3的系数是________,次数是________;
(3)-3x2+3x是________次________项式;
(4)若- ambn与5a2bcp为同类项,则m=______,n=______,p=________;
(5)当x=2,y=1时,x-3y的值为______,此时3+2x-6y的值为________.
①③⑤
②④⑥⑦
2
5
二
二
2
1
0
-1
1
例2 判断下列运算的正误:
(1)x2+4x2=5x4 ( )
(2)2x-3x2=-x ( )
(3)3a2·2a3=5a5 ( )
(4)(-2a3b2)2=4a6b4 ( )
(5)12m6n2÷(-4m3n)=-3m3n ( )
(6)(a-2b)2=a2-4ab+4b2 ( )
(7)(2-a)(a+2)=a2-4 ( )
(8)(x-1)(x-2)=x2-3x-2 ( )
×
√
√
√
×
×
×
×
例3 根据题意解答下列各题:
(1)因式分解:5x2-5xy=________;
(2)因式分解:x2y-y3= _ ;
(3)因式分解:4x2+4xy+y2= ;
(4)因式分解:-x3y+6x2y-9xy= .
5x(x-y)
y(x-y)(x+y)
(2x+y)2
-xy(x-3)2
5年真题、副题“明”考法
命题点
整式的运算(5年4考)
1. 计算:(-2x2y)3=( )
A. -8x6y3 B. 8x6y3
C. -6x6y3 D. 6x5y3
2.下列计算正确的是( )
A. x2+3x2=4x4 B. x2y·2x3=2x6y
C. (6x3y2)÷(3x)=2x2 D. (-3x)2=9x2
A
D
3. 下列计算正确的是( )
A. 2a2·3a2=6a2 B. (-3a2b)2=6a4b2
C. (a-b)2=a2-b2 D. -a2+2a2=a2
4. 下列计算正确的是( )
A. 3a4-a4=3
B. (-5x3y2 )2=10x6y4
C. (x+1)(x-2)=x2-x-2
D. (ab-1)2=a2b2-1
D
C
5. 下列计算正确的是( )
A.a2+a3=a5
B.2x2·( xy)= x3y
C.(a-b)(-a-b)=a2-b2
D.(-2x2y)3=-6x6y3
B
点击链接至练习册
同课章节目录
