【中考数学总复习】第1课时 实 数 课件
文档属性
| 名称 | 【中考数学总复习】第1课时 实 数 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 14:50:29 | ||
图片预览








文档简介
(共23张PPT)
第一单元 数与式
第1课时 实 数
(5年14考,每年2~3道,以3道为主,实数的运算必考,8~11分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
中考试题中的数学文化
4
5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:七上第二章P23-P71;八上第二章P21-P25、P33-P40
人教:七上第一章P2-P52;七下第六章P53-P58
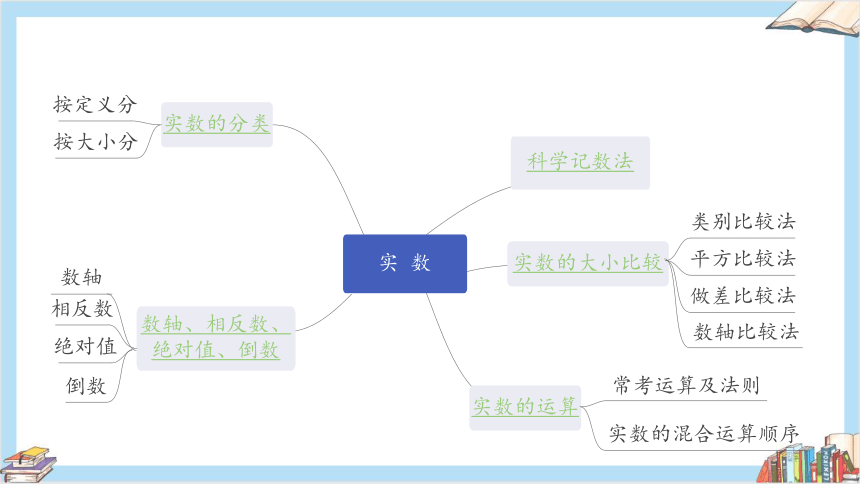
实数的分类
数轴、相反数、
绝对值、倒数
按定义分
按大小分
相反数
绝对值
倒数
数轴
科学记数法
实数的大小比较
类别比较法
平方比较法
做差比较法
数轴比较法
实数的运算
常考运算及法则
实数的混合运算顺序
实 数
实数的分类
考点
1
1.按定义分类
有理数
无理数:_____________小数
实数
整数
分数
无限不循环
有限小数或 小数
无限循环
【提分要点】常见的四种无理数类型:
(1)开方开不尽的数:如 , , 等;
(2)π及化简后含π的数:如 π, 等;
(3)有规律的无限不循环小数:如0.010010001…(相邻两个1之间依次多一个0)等;
(4)一些含有根式的三角函数值,如sin60°,tan30°等.
返回思维导图
(2)正负数的意义
正负数可以用于表示相反意义的量.如:规定“盈(+)”则“亏(-)”,“胜(+)”则“负(-)”,“收入(+)”则“支出(-)”,“零上(+)”则“零下(-)”,“上升(+)”则“下降(-)”等.
2. 按大小分
(1)实数
正数(>0)
(既不是正数,也不是负数)
负数(<0)
0
返回思维导图
数轴、相反数、绝对值、倒数
考点
2
1. 数轴
(1)三要素:
(2)实数与数轴上的点是一 一对应的.
2. 相反数
(1)非零实数a的相反数为________,特别地,0的相反数为0;
(2)实数a,b互为相反数 a+b=________;
(3)几何意义:互为相反数的两个数分别位于数轴上原点的两侧,且到原点的距离________;
-a
0
相等
返回思维导图
3.绝对值
(1)|a|=
a(a>0)
0(a=0)
(a<0)
-a
(2)几何意义:数轴上表示这个数的点到原点的距离, 离原点越远的数的绝对值越________.
4. 倒数
(1)实数a、b互为倒数 ab=______.
(2)非零实数a的倒数是________.特别注意:0没有倒数,倒数是它本身的数是±1.
大
1
返回思维导图
科学记数法
考点
3
表示形式:a×10n,其中______≤|a|<______,n是整数.
1. 对于一个绝对值大于10的数,n是正整数,它的值等于原数的整数位数减1或原数变为a时,小数点移动的位数.如:1950000000用科学记数法表示为 ,249530亿用科学记数法表示为 .
2. 对于一个绝对值大于0且小于1的数,n是负整数,它的绝对值等于原数左起第一个非零数字前零的个数或原数变为a时,小数点移动的位数.如:0.000067用科学记数法表示为 .
1
10
1.95×109
2.4953×1013
6.7×10-5
返回思维导图
实数的大小比较
考点
4
1. 数轴比较法:数轴上两个点表示的数,右边的总比左边的______.
2. 类别比较法:
(1)正数>0>负数;
(2)两个负数比较大小,_______大的数反而小.
3. 作差比较法:设两数分别为a、b.
(1)a-b>0 ______;
(2)a-b=0 a=b;
(3)a-b<0 ______.
4. 平方比较法: >b a___b2(a>0,b>0).(主要应用于含有根式的实数的大小比较)
大
绝对值
a>b
a<b
>
返回思维导图
实数的运算
考点
5
1. 常考运算及法则
(1)乘方:an=
a ·a · … · a
n个a
(2)-1的奇偶次幂:(-1 )n= ,如:(-1)2019=____,(-1)2020=____;
-1(n为奇数)
1(n为偶数)
(3)0次幂:a0(a≠0)=______,即遇到0次幂就写1;
(4)负整数指数幂:a-p=______(a≠0,p为正整数),特别地a-1=________;
1
1
-1
(5)去绝对值符号:|a-b|=
a-b(a>b)
0(a=b)
b-a(a<b)
返回思维导图
【提分要点】绝对值是非负数,因此在去绝对值符号时,先判断绝对值符号里面的数或式子的正负性,若为负,去绝对值符号时需改变其符号;若为正,直接去掉绝对值符号即可.
2. 实数的混合运算顺序
第一步:将包含每个小项的值计算出来;
第二步:根据实数的运算顺序计算:先乘除,后加减,有括号时先计算括号里面的,同级运算按照从左到右的顺序进行运算;
第三步:计算结果.
返回思维导图
典例“串”考点
例1 在实数3, , ,-1, , , ,sin45°,0,π,0.202002…(相邻两个2之间依次多一个0)中.
(1)无理数有 ,负数有 ;
(2)若规定零上3 ℃记作+3 ℃,则零下3 ℃可记作 ;
(3)如图,数轴上A,B两点表示的数之和为________;
,sin45°,π,0.202002…(相邻两个2之间依次多一个0)
-3 ℃
2
例1题图
(4) 的倒数为________,相反数为________,绝对值为________.
例2 把下列各数用科学记数法表示出来:
(1)1090000=________________;
(2)0.00031=________________;
(3)3240万=________________;
(4)258.9亿=________________.
例3 (1)比较大小:3____ ;
(2)实数3, , ,0,π中最小的数是________,将这组数据由小到大用“<”号连起来,可表示为______________________.
-4
1.09×106
3.1×10-4
3.24×107
2.589×1010
>
例4 (1)计算:|-3|=________,| -1|=________,
| -3|=________,-| -3|=________,
(π-1)0=________,(3- )0=________,
(-3)2=________,-3-1=________,
( )-1=________,( )-2=________ ;
(2)计算:3× +| -3|+(π-3)0;
3
1
1
9
-4
16
解:原式=3×(-2)+3- +1
=-2- .
(3)计算:- × -| -3|+( )-1.
解:原式=-2 -(3- )+4
=1- .
5年真题、副题“明”考法
命题点
1
实数的分类(2021.11)
1. (2021陕西11题3分)已知实数- ,0.16, ,π, , ,其中为无理数的是____________.
命题点
2
数轴、相反数、绝对值、 倒数
2. (西安)- 的倒数是( )
A. B. C. D.
3. (兰州) 的相反数是( )
A. B. C. D.
4. (2021陕西副题11题3分)如图,数轴上的A、B两点所表示的数分别为a、b,则a+b________0(填“>”,“=”或“<”).
第4题图
D
D
<
命题点
3
实数的大小比较
5. (2020武汉副题1题3分)下列四个实数中,最大的是( )
A. 2 B. C. 0 D. -1
6. (2021西宁11题3分)比较大小:3________ (填“>”、“<”或“=”).
7. (2020黄冈副题11题3分)比较大小: ____ (填“>”,“=”或“<”).
8. (2020三明11题3分)在实数-5,- ,0,π, 中,最大的一个数是________.
9. (2021怀化11题3分)将实数 ,π,0,-6由小到大用“<”号连起来,可表示为________________.
A
<
<
π
-6<0< <π
命题点
4
实数的运算
10. 计算:(-3)0=( )
A. 1 B. 0 C. 3 D. -
11. 计算:3-2=( )
A. B. C. -6 D. -
12. (2021青岛1题3分)计算:( )×2=( )
A. -1 B. 1 C. 4 D. -4
13. (2021襄阳1题3分)计算:( )2-1=( )
A. B. C. D. 0
A
B
A
C
解:原式=-2×(-3)+( -1)-4 (3分)
=6+ -5 (4分)
=1+ . (5分)
15. (2021陕西副题15题5分)计算:-2×( )2+| -3|-(-65)0.
解:原式=-2×3+(3- )-1 (3分)
=-6+3- -1 (4分)
=-4- . (5分)
14. 计算:-2× +|1- |-( )-2.
17. (2020绥化15题5分)计算:(- )× + | -2|-( )-1.
解:原式=- +2- -2 (3分)
= -
= . (5分)
16. (2018陕西15题5分)计算:(- )×(- )+| -1|+(5-2π)0.
解:原式= + -1+1 (3分)
= + -1+1
= . (5分)
20. (2021广州副题15题5分)计算: × -2×|-5|+(- )-2.
解:原式= -2×5+9 (3分)
= -10+9
= -1. (5分)
18.计算: -(π-5)0+|2 -3|.
解:原式= -1+3- (3分)
=2+ . (5分)
19. 计算:(-3)2+|2- |- .
解:原式=9+ -2- (3分)
=7- . (5分)
点击链接至练习册
第一单元 数与式
第1课时 实 数
(5年14考,每年2~3道,以3道为主,实数的运算必考,8~11分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
中考试题中的数学文化
4
5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:七上第二章P23-P71;八上第二章P21-P25、P33-P40
人教:七上第一章P2-P52;七下第六章P53-P58
实数的分类
数轴、相反数、
绝对值、倒数
按定义分
按大小分
相反数
绝对值
倒数
数轴
科学记数法
实数的大小比较
类别比较法
平方比较法
做差比较法
数轴比较法
实数的运算
常考运算及法则
实数的混合运算顺序
实 数
实数的分类
考点
1
1.按定义分类
有理数
无理数:_____________小数
实数
整数
分数
无限不循环
有限小数或 小数
无限循环
【提分要点】常见的四种无理数类型:
(1)开方开不尽的数:如 , , 等;
(2)π及化简后含π的数:如 π, 等;
(3)有规律的无限不循环小数:如0.010010001…(相邻两个1之间依次多一个0)等;
(4)一些含有根式的三角函数值,如sin60°,tan30°等.
返回思维导图
(2)正负数的意义
正负数可以用于表示相反意义的量.如:规定“盈(+)”则“亏(-)”,“胜(+)”则“负(-)”,“收入(+)”则“支出(-)”,“零上(+)”则“零下(-)”,“上升(+)”则“下降(-)”等.
2. 按大小分
(1)实数
正数(>0)
(既不是正数,也不是负数)
负数(<0)
0
返回思维导图
数轴、相反数、绝对值、倒数
考点
2
1. 数轴
(1)三要素:
(2)实数与数轴上的点是一 一对应的.
2. 相反数
(1)非零实数a的相反数为________,特别地,0的相反数为0;
(2)实数a,b互为相反数 a+b=________;
(3)几何意义:互为相反数的两个数分别位于数轴上原点的两侧,且到原点的距离________;
-a
0
相等
返回思维导图
3.绝对值
(1)|a|=
a(a>0)
0(a=0)
(a<0)
-a
(2)几何意义:数轴上表示这个数的点到原点的距离, 离原点越远的数的绝对值越________.
4. 倒数
(1)实数a、b互为倒数 ab=______.
(2)非零实数a的倒数是________.特别注意:0没有倒数,倒数是它本身的数是±1.
大
1
返回思维导图
科学记数法
考点
3
表示形式:a×10n,其中______≤|a|<______,n是整数.
1. 对于一个绝对值大于10的数,n是正整数,它的值等于原数的整数位数减1或原数变为a时,小数点移动的位数.如:1950000000用科学记数法表示为 ,249530亿用科学记数法表示为 .
2. 对于一个绝对值大于0且小于1的数,n是负整数,它的绝对值等于原数左起第一个非零数字前零的个数或原数变为a时,小数点移动的位数.如:0.000067用科学记数法表示为 .
1
10
1.95×109
2.4953×1013
6.7×10-5
返回思维导图
实数的大小比较
考点
4
1. 数轴比较法:数轴上两个点表示的数,右边的总比左边的______.
2. 类别比较法:
(1)正数>0>负数;
(2)两个负数比较大小,_______大的数反而小.
3. 作差比较法:设两数分别为a、b.
(1)a-b>0 ______;
(2)a-b=0 a=b;
(3)a-b<0 ______.
4. 平方比较法: >b a___b2(a>0,b>0).(主要应用于含有根式的实数的大小比较)
大
绝对值
a>b
a<b
>
返回思维导图
实数的运算
考点
5
1. 常考运算及法则
(1)乘方:an=
a ·a · … · a
n个a
(2)-1的奇偶次幂:(-1 )n= ,如:(-1)2019=____,(-1)2020=____;
-1(n为奇数)
1(n为偶数)
(3)0次幂:a0(a≠0)=______,即遇到0次幂就写1;
(4)负整数指数幂:a-p=______(a≠0,p为正整数),特别地a-1=________;
1
1
-1
(5)去绝对值符号:|a-b|=
a-b(a>b)
0(a=b)
b-a(a<b)
返回思维导图
【提分要点】绝对值是非负数,因此在去绝对值符号时,先判断绝对值符号里面的数或式子的正负性,若为负,去绝对值符号时需改变其符号;若为正,直接去掉绝对值符号即可.
2. 实数的混合运算顺序
第一步:将包含每个小项的值计算出来;
第二步:根据实数的运算顺序计算:先乘除,后加减,有括号时先计算括号里面的,同级运算按照从左到右的顺序进行运算;
第三步:计算结果.
返回思维导图
典例“串”考点
例1 在实数3, , ,-1, , , ,sin45°,0,π,0.202002…(相邻两个2之间依次多一个0)中.
(1)无理数有 ,负数有 ;
(2)若规定零上3 ℃记作+3 ℃,则零下3 ℃可记作 ;
(3)如图,数轴上A,B两点表示的数之和为________;
,sin45°,π,0.202002…(相邻两个2之间依次多一个0)
-3 ℃
2
例1题图
(4) 的倒数为________,相反数为________,绝对值为________.
例2 把下列各数用科学记数法表示出来:
(1)1090000=________________;
(2)0.00031=________________;
(3)3240万=________________;
(4)258.9亿=________________.
例3 (1)比较大小:3____ ;
(2)实数3, , ,0,π中最小的数是________,将这组数据由小到大用“<”号连起来,可表示为______________________.
-4
1.09×106
3.1×10-4
3.24×107
2.589×1010
>
例4 (1)计算:|-3|=________,| -1|=________,
| -3|=________,-| -3|=________,
(π-1)0=________,(3- )0=________,
(-3)2=________,-3-1=________,
( )-1=________,( )-2=________ ;
(2)计算:3× +| -3|+(π-3)0;
3
1
1
9
-4
16
解:原式=3×(-2)+3- +1
=-2- .
(3)计算:- × -| -3|+( )-1.
解:原式=-2 -(3- )+4
=1- .
5年真题、副题“明”考法
命题点
1
实数的分类(2021.11)
1. (2021陕西11题3分)已知实数- ,0.16, ,π, , ,其中为无理数的是____________.
命题点
2
数轴、相反数、绝对值、 倒数
2. (西安)- 的倒数是( )
A. B. C. D.
3. (兰州) 的相反数是( )
A. B. C. D.
4. (2021陕西副题11题3分)如图,数轴上的A、B两点所表示的数分别为a、b,则a+b________0(填“>”,“=”或“<”).
第4题图
D
D
<
命题点
3
实数的大小比较
5. (2020武汉副题1题3分)下列四个实数中,最大的是( )
A. 2 B. C. 0 D. -1
6. (2021西宁11题3分)比较大小:3________ (填“>”、“<”或“=”).
7. (2020黄冈副题11题3分)比较大小: ____ (填“>”,“=”或“<”).
8. (2020三明11题3分)在实数-5,- ,0,π, 中,最大的一个数是________.
9. (2021怀化11题3分)将实数 ,π,0,-6由小到大用“<”号连起来,可表示为________________.
A
<
<
π
-6<0< <π
命题点
4
实数的运算
10. 计算:(-3)0=( )
A. 1 B. 0 C. 3 D. -
11. 计算:3-2=( )
A. B. C. -6 D. -
12. (2021青岛1题3分)计算:( )×2=( )
A. -1 B. 1 C. 4 D. -4
13. (2021襄阳1题3分)计算:( )2-1=( )
A. B. C. D. 0
A
B
A
C
解:原式=-2×(-3)+( -1)-4 (3分)
=6+ -5 (4分)
=1+ . (5分)
15. (2021陕西副题15题5分)计算:-2×( )2+| -3|-(-65)0.
解:原式=-2×3+(3- )-1 (3分)
=-6+3- -1 (4分)
=-4- . (5分)
14. 计算:-2× +|1- |-( )-2.
17. (2020绥化15题5分)计算:(- )× + | -2|-( )-1.
解:原式=- +2- -2 (3分)
= -
= . (5分)
16. (2018陕西15题5分)计算:(- )×(- )+| -1|+(5-2π)0.
解:原式= + -1+1 (3分)
= + -1+1
= . (5分)
20. (2021广州副题15题5分)计算: × -2×|-5|+(- )-2.
解:原式= -2×5+9 (3分)
= -10+9
= -1. (5分)
18.计算: -(π-5)0+|2 -3|.
解:原式= -1+3- (3分)
=2+ . (5分)
19. 计算:(-3)2+|2- |- .
解:原式=9+ -2- (3分)
=7- . (5分)
点击链接至练习册
同课章节目录
