【中考数学总复习】第4课时 分 式 课件
文档属性
| 名称 | 【中考数学总复习】第4课时 分 式 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 14:50:29 | ||
图片预览





文档简介
(共18张PPT)
第一单元 数与式
第4课时 分 式
(5年4考,考则1道 ,3~5分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:八下第五章P108-P124;
人教:八上第十五章P126-P148.
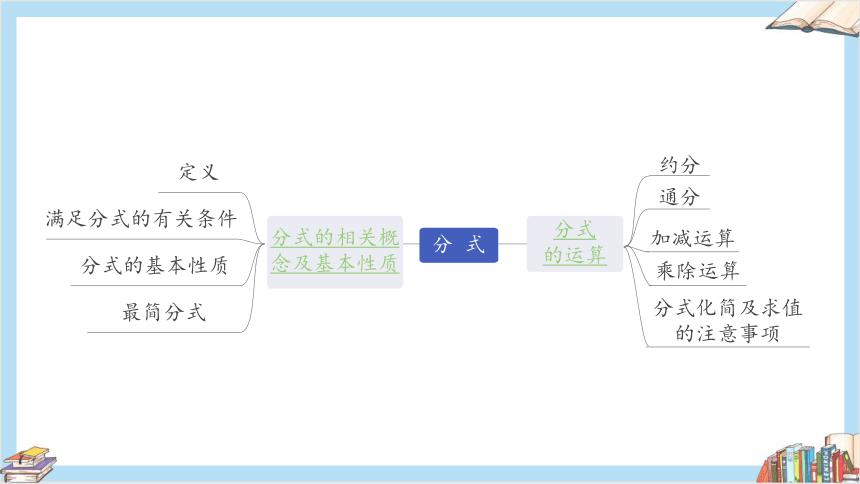
加减运算
通分
约分
分式
的运算
分式的相关概
念及基本性质
定义
最简分式
满足分式的有关条件
分 式
分式的基本性质
乘除运算
分式化简及求值
的注意事项
分式的相关概念及基本性质
考点
1
1. 定义:形如 (A,B是整式,且B中含有________,B_____0)的式子.
2. 满足分式的有关条件
(1)分式 有意义的条件:__________;
(2)分式 的值为0的条件:A____0且B______0.
3. 分式的基本性质
分式的分子与分母都乘或除以同一个________的整式,分式的值________.
即 = (用于通分)= (用于约分)(其中A、B、C是整式,且C≠0).
4. 最简分式:分子与分母没有________的分式.
字母
≠
B≠0
=
≠
不为零
不变
公因式
返回思维导图
分式的运算
考点
2
1. 约分:把一个分式的分子与分母的________约去.
约分的关键是确定公因式.
确定公因式的方法:
(1)分子、分母能因式分解的先因式分解;
(2)取分子、分母中相同因式的最低次幂(数字因式的最大公约数)的积作为公因式.
2. 通分:把几个异分母的分式分别化为与原来的分式相等的同分母的分式,叫做分式的通分.
公因式
返回思维导图
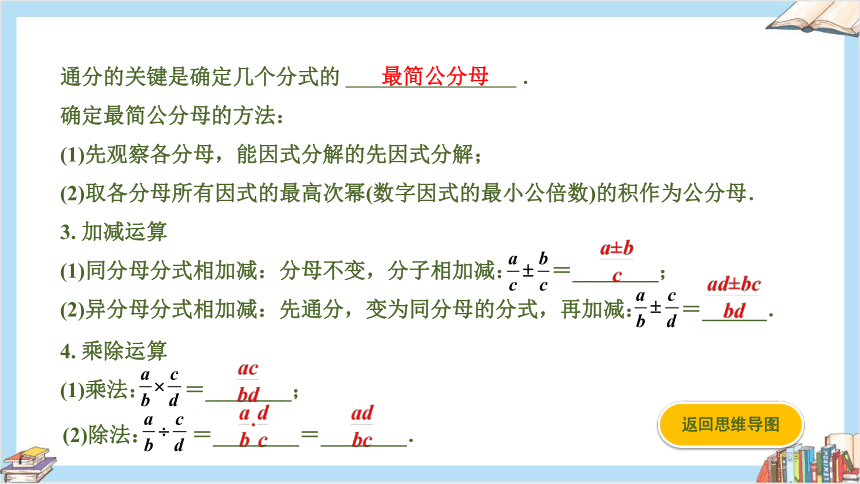
通分的关键是确定几个分式的 .
确定最简公分母的方法:
(1)先观察各分母,能因式分解的先因式分解;
(2)取各分母所有因式的最高次幂(数字因式的最小公倍数)的积作为公分母.
3. 加减运算
(1)同分母分式相加减:分母不变,分子相加减: =________;
(2)异分母分式相加减:先通分,变为同分母的分式,再加减: =______.
最简公分母
4. 乘除运算
(1)乘法: =________;
(2)除法: =________=________.
返回思维导图
5. 分式化简及求值的注意事项
(1)化简求值题一定要做到“先”化简,“再”求值;
(2)通分时要记得给不含分母的项乘最简公分母;
(3)化简结果应为最简分式或整式;
(4)求值时必须保证所“代”数值使原分式的分母及运算过程中分式的分母都不为0.
返回思维导图
典例“串”考点
例1 仔细观察下列各式,完成下列各题.
① ,② ,③ , ④ x+1, ⑤ .
(1)上列式子中,是分式的是________,是最简分式的是________,将 化为最简分式为____________;
(2)代数式 有意义的条件为________;
(3)代数式 值为零的条件为________.
①②③⑤
①②③
x≠-1
x=0
例2 (1)化简下列各式:
=________; =________;
1- =________; =________;
=________; =________;
a+1+ =________; -x+1=________.
(2)化简: ÷(1+ ).
(3)先化简,再求值:( )÷ ,其中x= .
5年真题、副题“明”考法
命题点
分式的化简(5年4考)
1. (2021西安5题3分)化简: ,结果正确的是( )
A. 1 B.
C. D. x2+y2
2. 化简:a+1- ,结果正确的是( )
A. B. 1 C. D.
类型一 加减运算(2017.5)
2a+1
B
D
类型二 混合运算(5年3考)
3. (2020兰州16题5分)化简:( )÷ .
4. (2019陕西16题5分)化简:( )÷ .
5. (2021梧州16题5分)化简:(x-5+ )÷ .
解:原式=
6. (2021南宁副题16题5分)化简:( )÷ .
解:原式=
点击链接至练习册
第一单元 数与式
第4课时 分 式
(5年4考,考则1道 ,3~5分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:八下第五章P108-P124;
人教:八上第十五章P126-P148.
加减运算
通分
约分
分式
的运算
分式的相关概
念及基本性质
定义
最简分式
满足分式的有关条件
分 式
分式的基本性质
乘除运算
分式化简及求值
的注意事项
分式的相关概念及基本性质
考点
1
1. 定义:形如 (A,B是整式,且B中含有________,B_____0)的式子.
2. 满足分式的有关条件
(1)分式 有意义的条件:__________;
(2)分式 的值为0的条件:A____0且B______0.
3. 分式的基本性质
分式的分子与分母都乘或除以同一个________的整式,分式的值________.
即 = (用于通分)= (用于约分)(其中A、B、C是整式,且C≠0).
4. 最简分式:分子与分母没有________的分式.
字母
≠
B≠0
=
≠
不为零
不变
公因式
返回思维导图
分式的运算
考点
2
1. 约分:把一个分式的分子与分母的________约去.
约分的关键是确定公因式.
确定公因式的方法:
(1)分子、分母能因式分解的先因式分解;
(2)取分子、分母中相同因式的最低次幂(数字因式的最大公约数)的积作为公因式.
2. 通分:把几个异分母的分式分别化为与原来的分式相等的同分母的分式,叫做分式的通分.
公因式
返回思维导图
通分的关键是确定几个分式的 .
确定最简公分母的方法:
(1)先观察各分母,能因式分解的先因式分解;
(2)取各分母所有因式的最高次幂(数字因式的最小公倍数)的积作为公分母.
3. 加减运算
(1)同分母分式相加减:分母不变,分子相加减: =________;
(2)异分母分式相加减:先通分,变为同分母的分式,再加减: =______.
最简公分母
4. 乘除运算
(1)乘法: =________;
(2)除法: =________=________.
返回思维导图
5. 分式化简及求值的注意事项
(1)化简求值题一定要做到“先”化简,“再”求值;
(2)通分时要记得给不含分母的项乘最简公分母;
(3)化简结果应为最简分式或整式;
(4)求值时必须保证所“代”数值使原分式的分母及运算过程中分式的分母都不为0.
返回思维导图
典例“串”考点
例1 仔细观察下列各式,完成下列各题.
① ,② ,③ , ④ x+1, ⑤ .
(1)上列式子中,是分式的是________,是最简分式的是________,将 化为最简分式为____________;
(2)代数式 有意义的条件为________;
(3)代数式 值为零的条件为________.
①②③⑤
①②③
x≠-1
x=0
例2 (1)化简下列各式:
=________; =________;
1- =________; =________;
=________; =________;
a+1+ =________; -x+1=________.
(2)化简: ÷(1+ ).
(3)先化简,再求值:( )÷ ,其中x= .
5年真题、副题“明”考法
命题点
分式的化简(5年4考)
1. (2021西安5题3分)化简: ,结果正确的是( )
A. 1 B.
C. D. x2+y2
2. 化简:a+1- ,结果正确的是( )
A. B. 1 C. D.
类型一 加减运算(2017.5)
2a+1
B
D
类型二 混合运算(5年3考)
3. (2020兰州16题5分)化简:( )÷ .
4. (2019陕西16题5分)化简:( )÷ .
5. (2021梧州16题5分)化简:(x-5+ )÷ .
解:原式=
6. (2021南宁副题16题5分)化简:( )÷ .
解:原式=
点击链接至练习册
同课章节目录
