【中考数学总复习】第6课时 一元二次方程 课件
文档属性
| 名称 | 【中考数学总复习】第6课时 一元二次方程 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第二单元 方程(组)与不等(组)
第6课时 一元二次方程
(近5年未单独考查)
目
录
点对点“过”考点
1
典例“串”考点
2
中考试题中的数学文化
3
点对点“过”考点
【对接教材】北师:九上第二章P31-P58;
人教:九上第二十一章P2-P26.
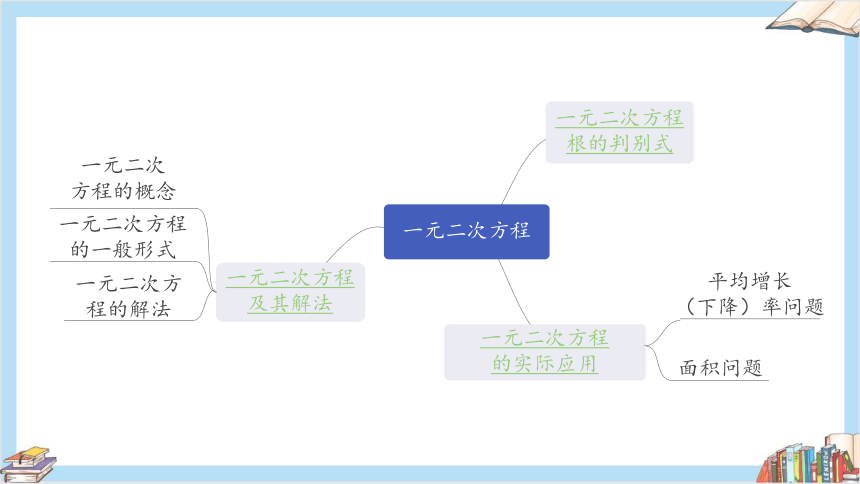
一元二次方
程的解法
一元二次方程
根的判别式
一元二次方程
的实际应用
一元二次方程
及其解法
一元二次
方程的概念
一元二次方程
的一般形式
平均增长
(下降)率问题
面积问题
一元二次方程
一元二次方程及其解法
考点
1
1. 一元二次方程的概念:只含有一个未知数,并且未知数的最高次数是________的整式方程.
2. 一元二次方程的一般形式:
2
返回思维导图
3. 一元二次方程的解法
解法 适用方程类型 方法或步骤
直接开平方法 ax2+c=0(a≠0,ac<0) 移项、系数化为1得x2= ,两边开方得x=±
形如(x+m)2=n(n≥0) 两边开方得x+m=± , 即x=± -m
配方法 所有一元二次方程,其中(1)当二次项系数化为1后,一次项系数为偶数时,使用配方法较简便;(2)各项的系数比较小,且便于配方 (1)若二次项系数不为1,先把系数化为1再配方,即x2+px+q=0;(2)把常数项移到方程的另一边,即x2+px=-q;(3)在方程两边同时加上____,即x2+px+____=-q+____;(4)把方程整理成(x+______)2=-q+______的形式;(5)运用直接开平方法解方程
返回思维导图
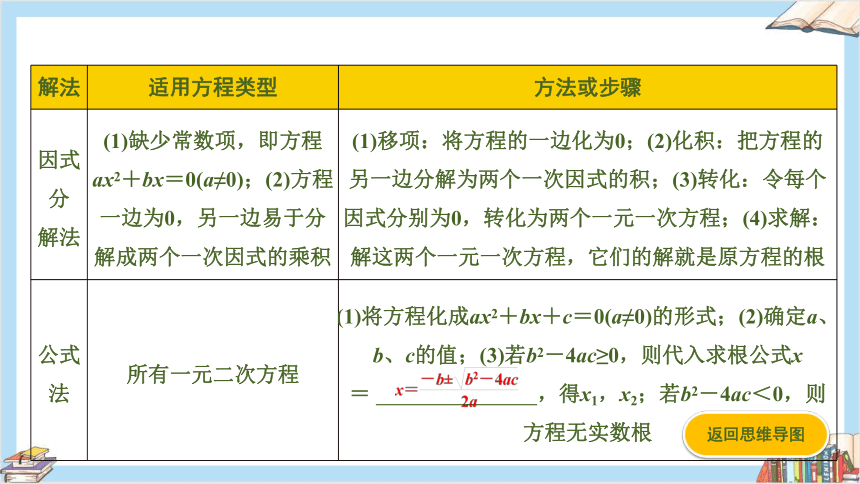
解法 适用方程类型 方法或步骤
因式分 解法 (1)缺少常数项,即方程ax2+bx=0(a≠0);(2)方程一边为0,另一边易于分解成两个一次因式的乘积 (1)移项:将方程的一边化为0;(2)化积:把方程的另一边分解为两个一次因式的积;(3)转化:令每个因式分别为0,转化为两个一元一次方程;(4)求解:解这两个一元一次方程,它们的解就是原方程的根
公式法 所有一元二次方程 (1)将方程化成ax2+bx+c=0(a≠0)的形式;(2)确定a、b、c的值;(3)若b2-4ac≥0,则代入求根公式x= ,得x1,x2;若b2-4ac<0,则方程无实数根
返回思维导图
一元二次方程根的判别式
考点
2
一元二次方程ax2+bx+c=0(a≠0)的根的判别式为b2-4ac.
1. b2-4ac________0 方程有两个不相等的实数根;
2. b2-4ac=0 方程有两个________的实数根;
3. b2-4ac____0 方程无实数根.
【提分要点】根的判别式的两个作用:1.不解方程,直接判断一元二次方程根的情况;2.根据方程根的情况,确定某个未知系数的值或取值范围.
>
相等
<
返回思维导图
一元二次方程的实际应用
考点
3
1. 平均增长(下降)率问题:
(1)增长率= ×100%;
(2)设a是基础量,m为平均增长率,2为增长次数,b为增长后的量,则b=_______;当m为平均下降率,2为下降次数,b为下降后的量,则b=________.
2. 面积问题:
(1)如图①,设空白部分的宽为x,则S阴影= ;
(2)如图②,设阴影道路的宽为x,则S空白= ;
a(1+m)2
a(1-m)2
(a-x)(b-x)
返回思维导图
(3)如图③,设阴影道路的宽为x,则S空白= ;
(4)如图④,围栏总长为a,BC的长为b,则S阴影=__________________.
(a-x)(b-x)
返回思维导图
回归教材
用配方法推导一元二次方程的求根公式
利用配方法解一元二次方程ax2+bx+c=0(a≠0).
【自主解答】
解:对于一元二次方程ax2+bx+c=0(a≠0),因为二次项系数a≠0,所以方程两边同除以a,得
配方得
∵a≠0,∴4a2>0.
当b2-4ac≥0时,
是一个非负数,此时两边开平方,得
典例“串”考点
例 已知关于x的方程(m-1)x2-4x-5=0.
(1)若该方程为一元二次方程,则m的取值范围为________;
(2)若m=2,请用三种不同的方法求解该方程.
方法一:
m≠1
方法一(因式分解法):
(x-5)(x+1)=0,
解得x1=5,x2=-1;
当m=2时,该方程为x2-4x-5=0.
方法二(公式法):由方程可知,a=1,b=-4,c=-5,
由x=
=
∴x1=5,x2=-1;
方法三:
方法三(配方法):配方得(x-2)2=9,
解得x1=5,x2=-1.
方法二:
(3)若x=1是该一元二次方程的一个根,则m的值为________,该方程的另一个根为________;
(4)若m=-3,则该一元二次方程根的情况是 ;
(5)若该一元二次方程有两个相等的实数根,则m的值为________;
(6)若该一元二次方程有两个不相等的实数根,则m的取值范围是 .
10
无实数根
点击链接至练习册
第二单元 方程(组)与不等(组)
第6课时 一元二次方程
(近5年未单独考查)
目
录
点对点“过”考点
1
典例“串”考点
2
中考试题中的数学文化
3
点对点“过”考点
【对接教材】北师:九上第二章P31-P58;
人教:九上第二十一章P2-P26.
一元二次方
程的解法
一元二次方程
根的判别式
一元二次方程
的实际应用
一元二次方程
及其解法
一元二次
方程的概念
一元二次方程
的一般形式
平均增长
(下降)率问题
面积问题
一元二次方程
一元二次方程及其解法
考点
1
1. 一元二次方程的概念:只含有一个未知数,并且未知数的最高次数是________的整式方程.
2. 一元二次方程的一般形式:
2
返回思维导图
3. 一元二次方程的解法
解法 适用方程类型 方法或步骤
直接开平方法 ax2+c=0(a≠0,ac<0) 移项、系数化为1得x2= ,两边开方得x=±
形如(x+m)2=n(n≥0) 两边开方得x+m=± , 即x=± -m
配方法 所有一元二次方程,其中(1)当二次项系数化为1后,一次项系数为偶数时,使用配方法较简便;(2)各项的系数比较小,且便于配方 (1)若二次项系数不为1,先把系数化为1再配方,即x2+px+q=0;(2)把常数项移到方程的另一边,即x2+px=-q;(3)在方程两边同时加上____,即x2+px+____=-q+____;(4)把方程整理成(x+______)2=-q+______的形式;(5)运用直接开平方法解方程
返回思维导图
解法 适用方程类型 方法或步骤
因式分 解法 (1)缺少常数项,即方程ax2+bx=0(a≠0);(2)方程一边为0,另一边易于分解成两个一次因式的乘积 (1)移项:将方程的一边化为0;(2)化积:把方程的另一边分解为两个一次因式的积;(3)转化:令每个因式分别为0,转化为两个一元一次方程;(4)求解:解这两个一元一次方程,它们的解就是原方程的根
公式法 所有一元二次方程 (1)将方程化成ax2+bx+c=0(a≠0)的形式;(2)确定a、b、c的值;(3)若b2-4ac≥0,则代入求根公式x= ,得x1,x2;若b2-4ac<0,则方程无实数根
返回思维导图
一元二次方程根的判别式
考点
2
一元二次方程ax2+bx+c=0(a≠0)的根的判别式为b2-4ac.
1. b2-4ac________0 方程有两个不相等的实数根;
2. b2-4ac=0 方程有两个________的实数根;
3. b2-4ac____0 方程无实数根.
【提分要点】根的判别式的两个作用:1.不解方程,直接判断一元二次方程根的情况;2.根据方程根的情况,确定某个未知系数的值或取值范围.
>
相等
<
返回思维导图
一元二次方程的实际应用
考点
3
1. 平均增长(下降)率问题:
(1)增长率= ×100%;
(2)设a是基础量,m为平均增长率,2为增长次数,b为增长后的量,则b=_______;当m为平均下降率,2为下降次数,b为下降后的量,则b=________.
2. 面积问题:
(1)如图①,设空白部分的宽为x,则S阴影= ;
(2)如图②,设阴影道路的宽为x,则S空白= ;
a(1+m)2
a(1-m)2
(a-x)(b-x)
返回思维导图
(3)如图③,设阴影道路的宽为x,则S空白= ;
(4)如图④,围栏总长为a,BC的长为b,则S阴影=__________________.
(a-x)(b-x)
返回思维导图
回归教材
用配方法推导一元二次方程的求根公式
利用配方法解一元二次方程ax2+bx+c=0(a≠0).
【自主解答】
解:对于一元二次方程ax2+bx+c=0(a≠0),因为二次项系数a≠0,所以方程两边同除以a,得
配方得
∵a≠0,∴4a2>0.
当b2-4ac≥0时,
是一个非负数,此时两边开平方,得
典例“串”考点
例 已知关于x的方程(m-1)x2-4x-5=0.
(1)若该方程为一元二次方程,则m的取值范围为________;
(2)若m=2,请用三种不同的方法求解该方程.
方法一:
m≠1
方法一(因式分解法):
(x-5)(x+1)=0,
解得x1=5,x2=-1;
当m=2时,该方程为x2-4x-5=0.
方法二(公式法):由方程可知,a=1,b=-4,c=-5,
由x=
=
∴x1=5,x2=-1;
方法三:
方法三(配方法):配方得(x-2)2=9,
解得x1=5,x2=-1.
方法二:
(3)若x=1是该一元二次方程的一个根,则m的值为________,该方程的另一个根为________;
(4)若m=-3,则该一元二次方程根的情况是 ;
(5)若该一元二次方程有两个相等的实数根,则m的值为________;
(6)若该一元二次方程有两个不相等的实数根,则m的取值范围是 .
10
无实数根
点击链接至练习册
同课章节目录
