【中考数学总复习】第8课时 一次不等式与一次不等式组 课件
文档属性
| 名称 | 【中考数学总复习】第8课时 一次不等式与一次不等式组 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第二单元 方程(组)与不等式(组)
第8课时 一次不等式与一次不等式组
(注:不含一次不等式组的实际应用)(5年2考,考则1道,3分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:八下第二章P36-P49、P54-P63
人教:七下第九章P113-P133.
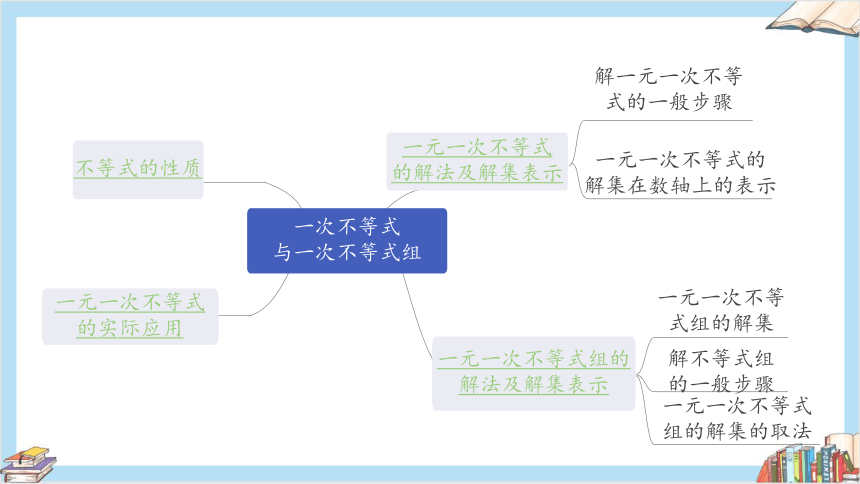
一元一次不等式
的解法及解集表示
一元一次不等式组的
解法及解集表示
解一元一次不等
式的一般步骤
一元一次不等式的
解集在数轴上的表示
一元一次不等
式组的解集
解不等式组
的一般步骤
不等式的性质
一元一次不等式
的实际应用
一元一次不等式
组的解集的取法
一次不等式
与一次不等式组
不等式的性质
考点
1
性质1:不等式两边同时加(或减)同一个数(或式子),不等号的方向不变.即若a>b,
则a±c____b±c;
性质2:不等式两边同时乘(或除以)同一个正数,不等号的方向不变.即若a>b,c
>0,则ac______bc或 ;
性质3:不等式两边同时乘(或除以)同一个负数,不等号的方向改变.即若a>b,c
<0,则ac______bc或 ______ .
【提分要点】在运用不等式的性质3时,不等号的方向要改变.
>
>
<
<
返回思维导图
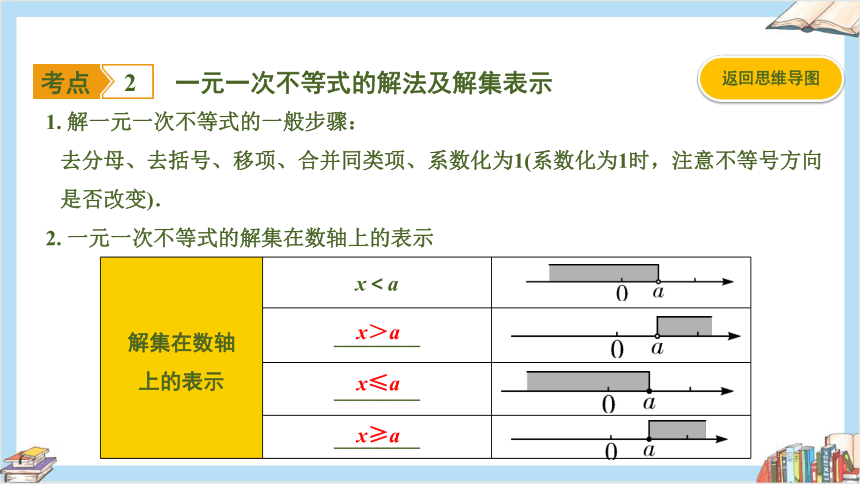
一元一次不等式的解法及解集表示
考点
2
1. 解一元一次不等式的一般步骤:
去分母、去括号、移项、合并同类项、系数化为1(系数化为1时,注意不等号方向
是否改变).
2. 一元一次不等式的解集在数轴上的表示
解集在数轴 上的表示 x<a
________
________
________
x>a
x≤a
x≥a
返回思维导图
【提分要点】在数轴上表示解集时,要注意“<”和“>”在数轴上表示为空心圆圈,“≤”和“≥”在数轴上表示为实心圆点.
返回思维导图
一元一次不等式组的解法及解集表示
考点
3
1. 一元一次不等式组的解集:一元一次不等式组各个不等式的解集的公共部分叫做这个一元一次不等式组的解集.
2. 解不等式组的一般步骤:
(1)解每一个一元一次不等式;
(2)在数轴上表示各不等式的解集;
(3)确定公共部分;
(4)写出不等式组的解集.
返回思维导图
3. 一元一次不等式组的解集的取法:
类型(a>b) 在数轴上的表示 口诀 解集
同大取大 ______
同小取小 x≤b
大小小大取中间 ______
大大小小取不了 无解
x≥a
b≤x≤a
返回思维导图
一元一次不等式的实际应用
考点
4
常见关键词与不等号的关系表:
常用关键词 符号
大于,多于,超过,高于 >
小于,少于,不足,低于 <
至少,不低于,不小于,不少于 ______
至多,不超过,不高于,不大于 ______
≥
≤
返回思维导图
典例“串”考点
例1 若a①a-1③ > ④a2例2 解不等式 >x-2;
解:去分母,得________________;
去括号,得________________;
移项,合并同类项,得________________;
系数化为1,得________________.
④
x-1>2(x-2)
x-1>2x-4
-x>-3
x<3
例3 解不等式组
(1)解不等式①,得____________;
(2)解不等式②,得____________;
(3)把不等式①和②的解集在数轴上表示出来:
(4)原不等式组的解集为____________;
(5)原不等式组的最小整数解为________;
例3题图
x>-4
例3题解图
-3
(3)不等式①②的解集在数轴上表示如解图:
(6)原不等式组的最大整数解为________;
(7)原不等式组的整数解的和为________.
【提分要点】
1. 解不等式时要注意正确运用不等式的性质3,即在不等式两边同时乘或除以同一个负数时,不等号要改变方向.
2. 求整数解时,“实心”所表示的实数如果是整数,则该点也是一个解,如果不是整数,则要从解集中离该点最近的整数点开始算起;“空心”所表示的实数如果是整数,则整数解取不到该点,如果不是整数,则要从解集中离该点最近的整数点开始算起.若求最大整数解,则找数轴上最右边的整数解;若求最小整数解,则找数轴上最左边的整数解.
0
-6
5年真题、副题“明”考法
命题点
1
一元一次不等式的解法
1. (2021洛阳11题3分)不等式 x+3<0的解集是________.
2. (2020西宁副题11题3分)不等式-2x+1>-5的最大整数解是________.
x>6
2
命题点
2
一元一次不等式组的解法
3. (2020陕西7题3分)不等式组 的最大整数解为( )
A. 8 B. 6 C. 5 D. 4
C
命题点
3
一元一次不等式的实际应用
4. (2021福州题7题3分)张老师准备用200元购买A、B两种笔记本共30本,并将这些笔记本奖给期末进步的学生.已知A种笔记本每本5元,B种笔记本每本8元,则张老师最多能购买B种笔记本( )
A. 18本 B. 17本
C. 16本 D. 15本
C
点击链接至练习册
第二单元 方程(组)与不等式(组)
第8课时 一次不等式与一次不等式组
(注:不含一次不等式组的实际应用)(5年2考,考则1道,3分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:八下第二章P36-P49、P54-P63
人教:七下第九章P113-P133.
一元一次不等式
的解法及解集表示
一元一次不等式组的
解法及解集表示
解一元一次不等
式的一般步骤
一元一次不等式的
解集在数轴上的表示
一元一次不等
式组的解集
解不等式组
的一般步骤
不等式的性质
一元一次不等式
的实际应用
一元一次不等式
组的解集的取法
一次不等式
与一次不等式组
不等式的性质
考点
1
性质1:不等式两边同时加(或减)同一个数(或式子),不等号的方向不变.即若a>b,
则a±c____b±c;
性质2:不等式两边同时乘(或除以)同一个正数,不等号的方向不变.即若a>b,c
>0,则ac______bc或 ;
性质3:不等式两边同时乘(或除以)同一个负数,不等号的方向改变.即若a>b,c
<0,则ac______bc或 ______ .
【提分要点】在运用不等式的性质3时,不等号的方向要改变.
>
>
<
<
返回思维导图
一元一次不等式的解法及解集表示
考点
2
1. 解一元一次不等式的一般步骤:
去分母、去括号、移项、合并同类项、系数化为1(系数化为1时,注意不等号方向
是否改变).
2. 一元一次不等式的解集在数轴上的表示
解集在数轴 上的表示 x<a
________
________
________
x>a
x≤a
x≥a
返回思维导图
【提分要点】在数轴上表示解集时,要注意“<”和“>”在数轴上表示为空心圆圈,“≤”和“≥”在数轴上表示为实心圆点.
返回思维导图
一元一次不等式组的解法及解集表示
考点
3
1. 一元一次不等式组的解集:一元一次不等式组各个不等式的解集的公共部分叫做这个一元一次不等式组的解集.
2. 解不等式组的一般步骤:
(1)解每一个一元一次不等式;
(2)在数轴上表示各不等式的解集;
(3)确定公共部分;
(4)写出不等式组的解集.
返回思维导图
3. 一元一次不等式组的解集的取法:
类型(a>b) 在数轴上的表示 口诀 解集
同大取大 ______
同小取小 x≤b
大小小大取中间 ______
大大小小取不了 无解
x≥a
b≤x≤a
返回思维导图
一元一次不等式的实际应用
考点
4
常见关键词与不等号的关系表:
常用关键词 符号
大于,多于,超过,高于 >
小于,少于,不足,低于 <
至少,不低于,不小于,不少于 ______
至多,不超过,不高于,不大于 ______
≥
≤
返回思维导图
典例“串”考点
例1 若a
解:去分母,得________________;
去括号,得________________;
移项,合并同类项,得________________;
系数化为1,得________________.
④
x-1>2(x-2)
x-1>2x-4
-x>-3
x<3
例3 解不等式组
(1)解不等式①,得____________;
(2)解不等式②,得____________;
(3)把不等式①和②的解集在数轴上表示出来:
(4)原不等式组的解集为____________;
(5)原不等式组的最小整数解为________;
例3题图
x>-4
例3题解图
-3
(3)不等式①②的解集在数轴上表示如解图:
(6)原不等式组的最大整数解为________;
(7)原不等式组的整数解的和为________.
【提分要点】
1. 解不等式时要注意正确运用不等式的性质3,即在不等式两边同时乘或除以同一个负数时,不等号要改变方向.
2. 求整数解时,“实心”所表示的实数如果是整数,则该点也是一个解,如果不是整数,则要从解集中离该点最近的整数点开始算起;“空心”所表示的实数如果是整数,则整数解取不到该点,如果不是整数,则要从解集中离该点最近的整数点开始算起.若求最大整数解,则找数轴上最右边的整数解;若求最小整数解,则找数轴上最左边的整数解.
0
-6
5年真题、副题“明”考法
命题点
1
一元一次不等式的解法
1. (2021洛阳11题3分)不等式 x+3<0的解集是________.
2. (2020西宁副题11题3分)不等式-2x+1>-5的最大整数解是________.
x>6
2
命题点
2
一元一次不等式组的解法
3. (2020陕西7题3分)不等式组 的最大整数解为( )
A. 8 B. 6 C. 5 D. 4
C
命题点
3
一元一次不等式的实际应用
4. (2021福州题7题3分)张老师准备用200元购买A、B两种笔记本共30本,并将这些笔记本奖给期末进步的学生.已知A种笔记本每本5元,B种笔记本每本8元,则张老师最多能购买B种笔记本( )
A. 18本 B. 17本
C. 16本 D. 15本
C
点击链接至练习册
同课章节目录
