【中考数学总复习】第12课时 反比例函数 课件
文档属性
| 名称 | 【中考数学总复习】第12课时 反比例函数 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 14:50:29 | ||
图片预览







文档简介
(共24张PPT)
第三单元 函 数
第12课时 反比例函数
(每年第13题必考, 3分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:九上第六章P148-P162;
人教:九下第二十六章P1-P22.
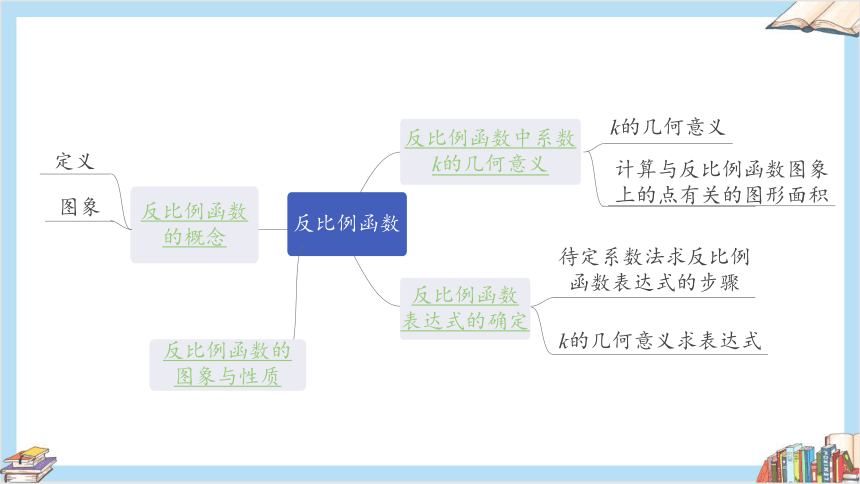
反比例函数
的概念
反比例函数中系数
k的几何意义
反比例函数
表达式的确定
定义
图象
k的几何意义
待定系数法求反比例
函数表达式的步骤
k的几何意义求表达式
计算与反比例函数图象
上的点有关的图形面积
反比例函数
反比例函数的
图象与性质
反比例函数的概念
考点
1
1. 定义:一般地,形如 (k为常数,k≠0)的函数叫做反比例函数.
2. 图象:反比例函数 (k为常数,k≠0)的图象是双曲线.图象上点的横纵坐标之积为定值,即xy=______.
k
返回思维导图
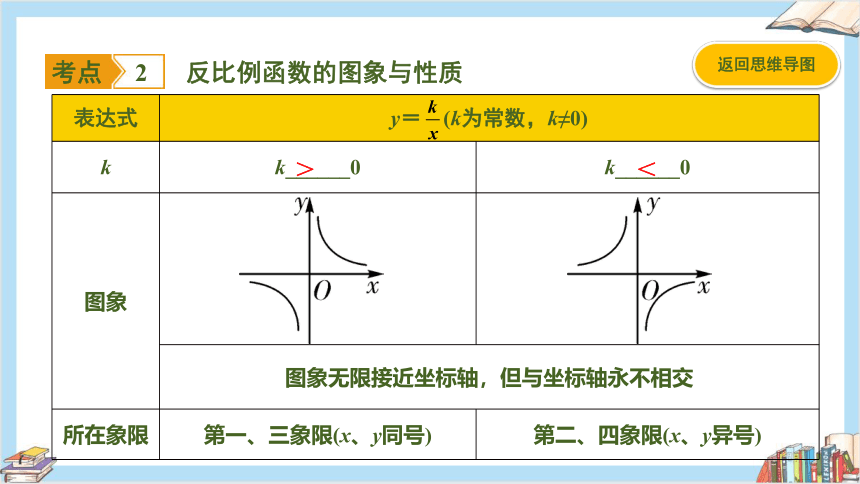
反比例函数的图象与性质
考点
2
表达式 y= (k为常数,k≠0) k k______0 k______0
图象
图象无限接近坐标轴,但与坐标轴永不相交 所在象限 第一、三象限(x、y同号) 第二、四象限(x、y异号)
>
<
返回思维导图
表达式 y=(k为常数,k≠0) 增减性 在每一象限,y随x的增大_______ 在每一象限,y随x的增大而______
对称性 中心对称 关于原点成中心对称,如双曲线一支上的点A(a,b)关于原点的对称点A′ 在双曲线另一支上 轴对称 关于直线y=x或y=-x成轴对称 减小
增大
(-a,-b)
返回思维导图
【提分要点】对于反比例函数图象上的几个点,如果已知横坐标,需要比较纵坐标的大小,或已知纵坐标,需要比较横坐标的大小,解题方法为:先判断这几个点是否在同一象限内,若不在同一象限内,则通过判断函数值的正负即可进行比较;若在同一象限内,则可以根据反比例函数的增减性来进行解答.另外,也可以代值或取特殊值比较大小.
返回思维导图
反比例函数中系数k的几何意义
考点
3
1. k的几何意义:
如图,过反比例函数 (k≠0)上任一点P(x,y)作x轴、y轴的垂线PM、PN,与坐标轴围成的矩形PMON的面积S=|xy|=________.
|k|
返回思维导图
2. 计算与反比例函数图象上的点有关的图形面积
返回思维导图
返回思维导图
反比例函数表达式的确定
考点
4
1. 待定系数法求反比例函数表达式的步骤:
(1)设所求的反比例函数表达式为: (k≠0);
(2)找出在反比例函数图象上的点P(a,b);
(3)将点P的坐标代入 中,得k=ab;
(4)确定反比例函数表达式为: .
2. k的几何意义求表达式:已知图形面积时,优先考虑利用k的几何意义.由面积得|k|,再结合图象所在象限判断k的正负,从而得出k的值,代入表达式即可.
返回思维导图
典例“串”考点
例1 已知反比例函数 .
(1)m的取值范围是________;
(2)当反比例函数的图象如图所示时,m的取值范围为________;
(3)若该函数的图象经过点A(3,-2),B(a,6),则m=______,a=________;
(4)若点P(x,y)在反比例函数图象上,则点Q(-x,-y)________该反比例函数图象上;(填“在”或“不在”)
(5)若m>1,点A(-1,y1),B(1,y2)和C(2,y3)都在该函数图象上.则y1 ,y2 ,y3的大小关系为 (用“<”连接);
m≠1
m<1
-5
-1
在
y1 <y3 <y2
(6)若该反比例函数图象经过点(2,4),当y>-2时,则x的取值范围是 ;
(7)已知点A是该反比例函数图象上一点,点B是反比例函数 上一点,若A,B两点关于y轴对称,则m的值为________.
x<-4或x>0
例1题图
例2 已知反比例函数 (k≠0),点A是该函数图象上一点.
(1)如图①,过点A作AB⊥x轴,点C在y轴上,若k=3,则△ABC的面积为________;
(2)如图②,点B是反比例函数 图象上一点,且AB∥x轴,点C在x轴上,若k=
12,则△ABC的面积为________.
(3)如图③,点B是反比例函数 图象上一点,连接OA、OB,若OA⊥OB,
OB=2OA,则k=________;
例2题图
4
例3 已知反比例函数 与一次函数图象交于A、B两点.
(1)若一次函数的表达式为y=-4x,点A的纵坐标坐标为2,则反比例函数的表达式为________,点B的坐标为________;
(2)若一次函数y=x+b与该反比例函数图象的交点A的坐标为(2,5),则b=______,k=________,点B的坐标为 ,△OAB的面积为_____;
3
10
(-5,-2)
例3题图
(3)若一次函数y=ax+b与该反比例函数图象的交点分别为A(1,6),B(m,-2),则不等式ax+b> 的解集为 ;
(4)如图,直线AB与该反比例函数y= (x>0)的图象如图所示,直线AB交x轴于点C,点B为线段AC的中点,连接OA.若S△OAC=12,则该反比例函数的表达式为_______.
x>1或-3<x<0
陕西5年真题、副题“明”考法
命题点
1
反比例函数图象上点的特征(5年3考)
1. (2018陕西13题3分)若一个反比例函数的图象经过点A(m,m)和B(2m,-1),则这个反比例函数的表达式为________.
2. (2015陕西副题13题3分)在平面直角坐标系中,反比例函数y= 的图象位于第二、四象限,且经过点(1,k2-2),则k的值为________.
3. (2017陕西13题3分)已知A,B两点分别在反比例函数y= (m≠0)和y= (m≠ )的图象上.若点A与点B关于x轴对称,则m的值为________.
-1
1
4.(2019陕西13题3分)如图,D是矩形AOBC的对称中心,A(0,4),B(6,0).若一个反比例函数的图象经过点D,交AC于点M,则点M的坐标为________.
第4题图
命题点
2
与反比例函数图象上的点有关的面积问题(2015.13)
5. (2019陕西副题13题3分)如图,在平面直角坐标系中,正方形OABC的面积为4,边OA、OC分别在x轴、y轴上,一个反比例函数的图象经过点B.若该函数图象上的点P到y轴的距离是这个正方形边长的一半,则点P的坐标为__________________
第5题图
(1,4)或(-1,-4)
6. (2015陕西13题3分)如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y= 的图象交于A、B两点,则四边形MAOB的面积为________.
10
第6题图
7. (2016陕西副题13题3分)如图,在x轴上方,平行于x轴的直线与反比例函数y=和y= 的图象分别交于A、B两点,连接OA、OB.若△AOB的面积为6,则k1-k2=________.
-12
第7题图
命题点
3
反比例函数与一次函数综合题(2016.13)
8. (2018陕西副题13题3分)若一个反比例函数的图象与直线y=-2x+6的一个交点为A(m,-4),则这个反比例函数的表达式是__________.
9. (2017陕西副题13题3分)若正比例函数y= 的图象与反比例函数y= (k≠ )的图象有公共点,则k的取值范围是________.
10. (2016陕西13题3分)已知一次函数y=2x+4的图象分别交x轴、y轴于A、B两点.
若这个一次函数的图象与一个反比例函数的图象在第一象限交于点C,且AB=2BC,
则这个反比例函数的表达式为________.
点击链接至练习册
第三单元 函 数
第12课时 反比例函数
(每年第13题必考, 3分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:九上第六章P148-P162;
人教:九下第二十六章P1-P22.
反比例函数
的概念
反比例函数中系数
k的几何意义
反比例函数
表达式的确定
定义
图象
k的几何意义
待定系数法求反比例
函数表达式的步骤
k的几何意义求表达式
计算与反比例函数图象
上的点有关的图形面积
反比例函数
反比例函数的
图象与性质
反比例函数的概念
考点
1
1. 定义:一般地,形如 (k为常数,k≠0)的函数叫做反比例函数.
2. 图象:反比例函数 (k为常数,k≠0)的图象是双曲线.图象上点的横纵坐标之积为定值,即xy=______.
k
返回思维导图
反比例函数的图象与性质
考点
2
表达式 y= (k为常数,k≠0) k k______0 k______0
图象
图象无限接近坐标轴,但与坐标轴永不相交 所在象限 第一、三象限(x、y同号) 第二、四象限(x、y异号)
>
<
返回思维导图
表达式 y=(k为常数,k≠0) 增减性 在每一象限,y随x的增大_______ 在每一象限,y随x的增大而______
对称性 中心对称 关于原点成中心对称,如双曲线一支上的点A(a,b)关于原点的对称点A′ 在双曲线另一支上 轴对称 关于直线y=x或y=-x成轴对称 减小
增大
(-a,-b)
返回思维导图
【提分要点】对于反比例函数图象上的几个点,如果已知横坐标,需要比较纵坐标的大小,或已知纵坐标,需要比较横坐标的大小,解题方法为:先判断这几个点是否在同一象限内,若不在同一象限内,则通过判断函数值的正负即可进行比较;若在同一象限内,则可以根据反比例函数的增减性来进行解答.另外,也可以代值或取特殊值比较大小.
返回思维导图
反比例函数中系数k的几何意义
考点
3
1. k的几何意义:
如图,过反比例函数 (k≠0)上任一点P(x,y)作x轴、y轴的垂线PM、PN,与坐标轴围成的矩形PMON的面积S=|xy|=________.
|k|
返回思维导图
2. 计算与反比例函数图象上的点有关的图形面积
返回思维导图
返回思维导图
反比例函数表达式的确定
考点
4
1. 待定系数法求反比例函数表达式的步骤:
(1)设所求的反比例函数表达式为: (k≠0);
(2)找出在反比例函数图象上的点P(a,b);
(3)将点P的坐标代入 中,得k=ab;
(4)确定反比例函数表达式为: .
2. k的几何意义求表达式:已知图形面积时,优先考虑利用k的几何意义.由面积得|k|,再结合图象所在象限判断k的正负,从而得出k的值,代入表达式即可.
返回思维导图
典例“串”考点
例1 已知反比例函数 .
(1)m的取值范围是________;
(2)当反比例函数的图象如图所示时,m的取值范围为________;
(3)若该函数的图象经过点A(3,-2),B(a,6),则m=______,a=________;
(4)若点P(x,y)在反比例函数图象上,则点Q(-x,-y)________该反比例函数图象上;(填“在”或“不在”)
(5)若m>1,点A(-1,y1),B(1,y2)和C(2,y3)都在该函数图象上.则y1 ,y2 ,y3的大小关系为 (用“<”连接);
m≠1
m<1
-5
-1
在
y1 <y3 <y2
(6)若该反比例函数图象经过点(2,4),当y>-2时,则x的取值范围是 ;
(7)已知点A是该反比例函数图象上一点,点B是反比例函数 上一点,若A,B两点关于y轴对称,则m的值为________.
x<-4或x>0
例1题图
例2 已知反比例函数 (k≠0),点A是该函数图象上一点.
(1)如图①,过点A作AB⊥x轴,点C在y轴上,若k=3,则△ABC的面积为________;
(2)如图②,点B是反比例函数 图象上一点,且AB∥x轴,点C在x轴上,若k=
12,则△ABC的面积为________.
(3)如图③,点B是反比例函数 图象上一点,连接OA、OB,若OA⊥OB,
OB=2OA,则k=________;
例2题图
4
例3 已知反比例函数 与一次函数图象交于A、B两点.
(1)若一次函数的表达式为y=-4x,点A的纵坐标坐标为2,则反比例函数的表达式为________,点B的坐标为________;
(2)若一次函数y=x+b与该反比例函数图象的交点A的坐标为(2,5),则b=______,k=________,点B的坐标为 ,△OAB的面积为_____;
3
10
(-5,-2)
例3题图
(3)若一次函数y=ax+b与该反比例函数图象的交点分别为A(1,6),B(m,-2),则不等式ax+b> 的解集为 ;
(4)如图,直线AB与该反比例函数y= (x>0)的图象如图所示,直线AB交x轴于点C,点B为线段AC的中点,连接OA.若S△OAC=12,则该反比例函数的表达式为_______.
x>1或-3<x<0
陕西5年真题、副题“明”考法
命题点
1
反比例函数图象上点的特征(5年3考)
1. (2018陕西13题3分)若一个反比例函数的图象经过点A(m,m)和B(2m,-1),则这个反比例函数的表达式为________.
2. (2015陕西副题13题3分)在平面直角坐标系中,反比例函数y= 的图象位于第二、四象限,且经过点(1,k2-2),则k的值为________.
3. (2017陕西13题3分)已知A,B两点分别在反比例函数y= (m≠0)和y= (m≠ )的图象上.若点A与点B关于x轴对称,则m的值为________.
-1
1
4.(2019陕西13题3分)如图,D是矩形AOBC的对称中心,A(0,4),B(6,0).若一个反比例函数的图象经过点D,交AC于点M,则点M的坐标为________.
第4题图
命题点
2
与反比例函数图象上的点有关的面积问题(2015.13)
5. (2019陕西副题13题3分)如图,在平面直角坐标系中,正方形OABC的面积为4,边OA、OC分别在x轴、y轴上,一个反比例函数的图象经过点B.若该函数图象上的点P到y轴的距离是这个正方形边长的一半,则点P的坐标为__________________
第5题图
(1,4)或(-1,-4)
6. (2015陕西13题3分)如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y= 的图象交于A、B两点,则四边形MAOB的面积为________.
10
第6题图
7. (2016陕西副题13题3分)如图,在x轴上方,平行于x轴的直线与反比例函数y=和y= 的图象分别交于A、B两点,连接OA、OB.若△AOB的面积为6,则k1-k2=________.
-12
第7题图
命题点
3
反比例函数与一次函数综合题(2016.13)
8. (2018陕西副题13题3分)若一个反比例函数的图象与直线y=-2x+6的一个交点为A(m,-4),则这个反比例函数的表达式是__________.
9. (2017陕西副题13题3分)若正比例函数y= 的图象与反比例函数y= (k≠ )的图象有公共点,则k的取值范围是________.
10. (2016陕西13题3分)已知一次函数y=2x+4的图象分别交x轴、y轴于A、B两点.
若这个一次函数的图象与一个反比例函数的图象在第一象限交于点C,且AB=2BC,
则这个反比例函数的表达式为________.
点击链接至练习册
同课章节目录
