【中考数学总复习】第7课时 分式方程 课件
文档属性
| 名称 | 【中考数学总复习】第7课时 分式方程 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 14:50:29 | ||
图片预览





文档简介
(共15张PPT)
第二单元 方程(组)与不等式(组)
第7课时 分式方程
(5年2考,考则1道, 5分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:八下第五章P125-P130;
人教:八上第十五章P149-P159.
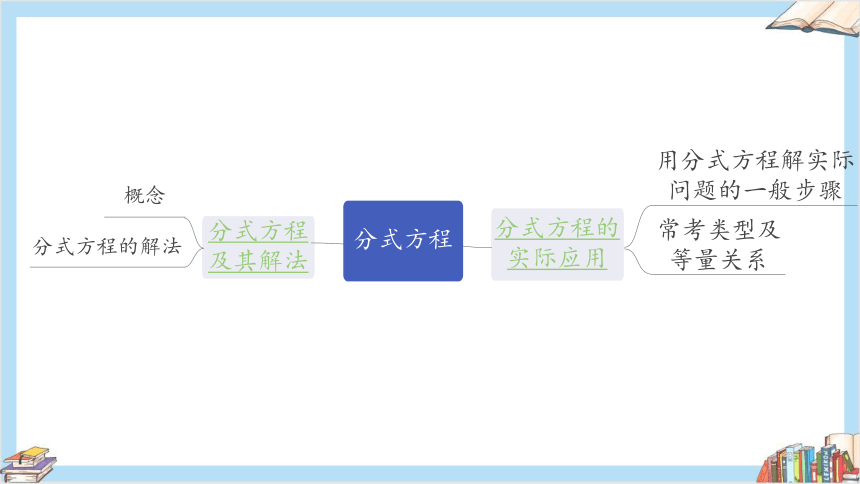
分式方程
及其解法
分式方程的解法
概念
分式方程的
实际应用
用分式方程解实际
问题的一般步骤
常考类型及
等量关系
分式方程
分式方程及其解法
考点
1
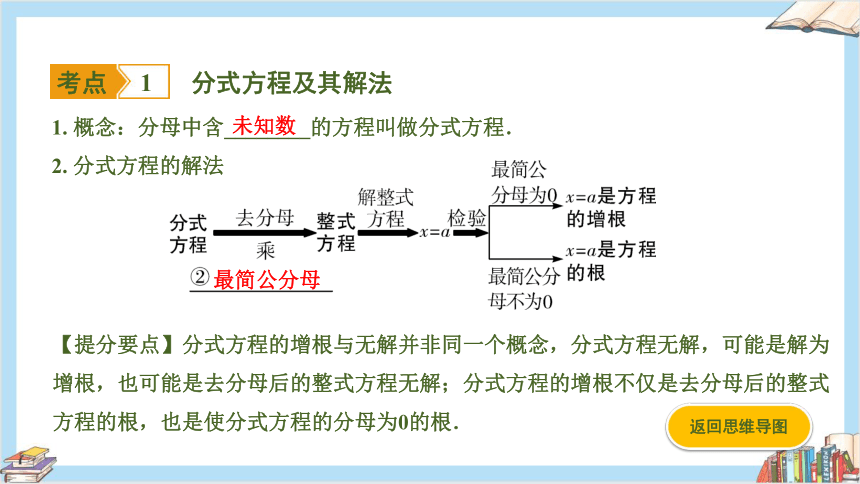
1. 概念:分母中含________的方程叫做分式方程.
2. 分式方程的解法
未知数
最简公分母
【提分要点】分式方程的增根与无解并非同一个概念,分式方程无解,可能是解为增根,也可能是去分母后的整式方程无解;分式方程的增根不仅是去分母后的整式方程的根,也是使分式方程的分母为0的根.
返回思维导图
分式方程的实际应用
考点
2
1. 用分式方程解实际问题的一般步骤
【提分要点】双检验:(1)检验是否是分式方程的解;(2)检验是否符合实际问题.
返回思维导图
2. 常考类型及等量关系
常考类型 数量关系
行程问题
工程问题 =工作完成时间
特别地,有时工作总量可以看做整体“1”,这时,
销售问题 折扣= ,
=工作效率
标价=
=时间
返回思维导图
典例“串”考点
例 下列方程: = , =x, , .
(1)不是分式方程的是______________;
(2)解方程 时,首先需将其化为整式方程,方程两边要同时乘___________;
x(x-2)
(3)如下是求解方程 的过程:
移项、合并同类项得,x=-2,②
检验,当x=-2时,x=3≠0,③
∴原分式方程的解为x=-2.④
上述解答过程是从第________步开始出错的;请你写出正确的解答过程.
①
解:方程两边同乘(x-3)得,
2-x+3=-1,
移项,合并同类项得,x=6,
检验:当x=6时,x-3≠0,
∴该分式方程的解为x=6;
解:去分母得,2-x-3=1,①
(4)请你按照所给的步骤求解方程 .
2x(x-1)=2(x2-1)-1,
2x2-2x=2x2-2-1,
-2x=-3,
是原分式方程的解.
【提分要点】
1. 去分母时切记要给常数项或整式乘最简公分母,若分母与最简公分母互为相反数时,去分母要注意变号,且验根是解分式方程必不可少的环节;
2. 注意与分式化简(求值)的区别:两者都需找最简公分母,但分式化简(求值)的目的是约分,而分式方程的目的是去分母,切勿混淆.
5年真题、副题“明”考法
命题点
解分式方程(5年2考)
1. (2021襄阳16题5分)解方程: =1.
解:(x+3)2-2(x-3)=(x-3)(x+3),(2分)
解得x=-6.(4分)
经检验,x=-6是原方程的根.(5分)
解:(2x-1)(x-2)=2(x2-4)-3(x+2),(2分)
-2x=-16,(3分)
x=8.(4分)
经检验,x=8是原方程的根.(5分)
2. (2021柳州副题16题5分)解分式方程:
3. (2021海东副题16题5分)解方程: .
解:5x-8-(x2-9)=(3-x)(x-3)(2分)
5x-8-x2+9=-x2+6x-9(3分)
-x=-10
x=10.(4分)
经检验,x=10是原方程的根.(5分)
点击链接至练习册
第二单元 方程(组)与不等式(组)
第7课时 分式方程
(5年2考,考则1道, 5分)
目
录
点对点“过”考点
1
典例“串”考点
2
3
陕西5年真题、副题“明”考法
点对点“过”考点
【对接教材】北师:八下第五章P125-P130;
人教:八上第十五章P149-P159.
分式方程
及其解法
分式方程的解法
概念
分式方程的
实际应用
用分式方程解实际
问题的一般步骤
常考类型及
等量关系
分式方程
分式方程及其解法
考点
1
1. 概念:分母中含________的方程叫做分式方程.
2. 分式方程的解法
未知数
最简公分母
【提分要点】分式方程的增根与无解并非同一个概念,分式方程无解,可能是解为增根,也可能是去分母后的整式方程无解;分式方程的增根不仅是去分母后的整式方程的根,也是使分式方程的分母为0的根.
返回思维导图
分式方程的实际应用
考点
2
1. 用分式方程解实际问题的一般步骤
【提分要点】双检验:(1)检验是否是分式方程的解;(2)检验是否符合实际问题.
返回思维导图
2. 常考类型及等量关系
常考类型 数量关系
行程问题
工程问题 =工作完成时间
特别地,有时工作总量可以看做整体“1”,这时,
销售问题 折扣= ,
=工作效率
标价=
=时间
返回思维导图
典例“串”考点
例 下列方程: = , =x, , .
(1)不是分式方程的是______________;
(2)解方程 时,首先需将其化为整式方程,方程两边要同时乘___________;
x(x-2)
(3)如下是求解方程 的过程:
移项、合并同类项得,x=-2,②
检验,当x=-2时,x=3≠0,③
∴原分式方程的解为x=-2.④
上述解答过程是从第________步开始出错的;请你写出正确的解答过程.
①
解:方程两边同乘(x-3)得,
2-x+3=-1,
移项,合并同类项得,x=6,
检验:当x=6时,x-3≠0,
∴该分式方程的解为x=6;
解:去分母得,2-x-3=1,①
(4)请你按照所给的步骤求解方程 .
2x(x-1)=2(x2-1)-1,
2x2-2x=2x2-2-1,
-2x=-3,
是原分式方程的解.
【提分要点】
1. 去分母时切记要给常数项或整式乘最简公分母,若分母与最简公分母互为相反数时,去分母要注意变号,且验根是解分式方程必不可少的环节;
2. 注意与分式化简(求值)的区别:两者都需找最简公分母,但分式化简(求值)的目的是约分,而分式方程的目的是去分母,切勿混淆.
5年真题、副题“明”考法
命题点
解分式方程(5年2考)
1. (2021襄阳16题5分)解方程: =1.
解:(x+3)2-2(x-3)=(x-3)(x+3),(2分)
解得x=-6.(4分)
经检验,x=-6是原方程的根.(5分)
解:(2x-1)(x-2)=2(x2-4)-3(x+2),(2分)
-2x=-16,(3分)
x=8.(4分)
经检验,x=8是原方程的根.(5分)
2. (2021柳州副题16题5分)解分式方程:
3. (2021海东副题16题5分)解方程: .
解:5x-8-(x2-9)=(3-x)(x-3)(2分)
5x-8-x2+9=-x2+6x-9(3分)
-x=-10
x=10.(4分)
经检验,x=10是原方程的根.(5分)
点击链接至练习册
同课章节目录
