【中考数学总复习】第11课时 一次函数的实际应用 课件
文档属性
| 名称 | 【中考数学总复习】第11课时 一次函数的实际应用 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 14:50:29 | ||
图片预览









文档简介
(共34张PPT)
第三单元 函 数
第11课时 一次函数的实际应用
(每年第21题必考,7分)
目
录
典例“串”考点
1
2
5年真题、副题“明”考法
典例“串”考点
例1 碑林书法社小组用的书法练习纸(毛边纸)可以到甲商店购买,也可以到乙商店购买.已知两商店的标价都是每刀20元(每刀100张).甲商店的优惠条件是:若购买不超过10刀,则按标价卖,购买10刀以上,从第11刀开始按标价的七折卖;乙商店的优惠条件是:从第1刀开始按标价的八五折卖.设购买刀数为x(刀),在甲商店购买所需费用为y1元,在乙商店购买所需费用为y2元.
(1)写出y1,y2与x(x>0)之间的函数关系式;
(2)碑林书法社小组现有480元,最多可以买多少刀书法练习纸?
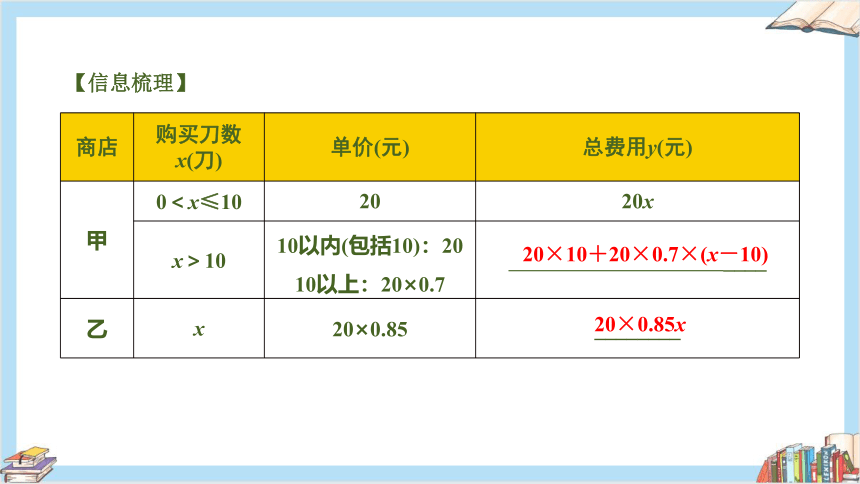
【信息梳理】
商店 购买刀数x(刀) 单价(元) 总费用y(元)
甲 0<x≤10 20 20x
x>10 10以内(包括10):20 10以上:20×0.7 ____
乙 x 20×0.85 ________
20×10+20×0.7×(x-10)
20×0.85x
(2)若在甲商店购买:则14x+60=480,解得x=30,
【自主解答】
例2 五一期间,甲、乙两人分别骑自行车和摩托车从A地出发前往B地郊游,并以各自的速度匀速行驶,到达目的地停止,途中乙休息了一段时间,然后又继续赶路.甲、乙两人各自行驶的路程y(km)与所用时间x(min)之间的函数图象如图所示.
(1)求乙休息后所行的路程y与x之间的函数关系式,并写出自变量x的取值范围;
(2)为了保证及时联络,甲、乙两人在第一次相遇时约定此后两人之间的距离不超过3 km,甲、乙两人是否遵守约定,并说明理由.
例2题图
【思维教练】(1)由图可知,A、B两地之间的距离为________km,甲骑自行车的速度是________km/min.乙休息后所行的路程y与x之间的函数图象经过的点为________和________;
(2)结合题图可知,求出乙开始休息时两人距离及乙刚到达B地时两人的距离,即可判断两人是否遵守约定.
【自主解答】
30
0.25
(50,10)
(80,20)
解:(1)由图可知,A、B两地相距30 km,甲骑自行车的速度为 =0.25 km/min,当甲出发80 min时,距离A地20 km,两人相遇.
设乙休息后所行的路程y与x之间的函数关系为y=kx+b(k≠0),
∵函数图象经过(50,10)和(80,20)两点,
当y=30时,x=110,
∴自变量x的取值范围为:50≤x≤110;
(2)当x=50时,甲行驶了50×0.25=12.5 km,
此时甲、乙之间的距离为12.5-10=2.5<3,遵守约定;
当x=110时,甲行驶了110×0.25=27.5 km,
此时乙到达B地,甲、乙之间的距离为30-27.5=2.5<3,遵守约定.
∴甲、乙两人遵守约定.
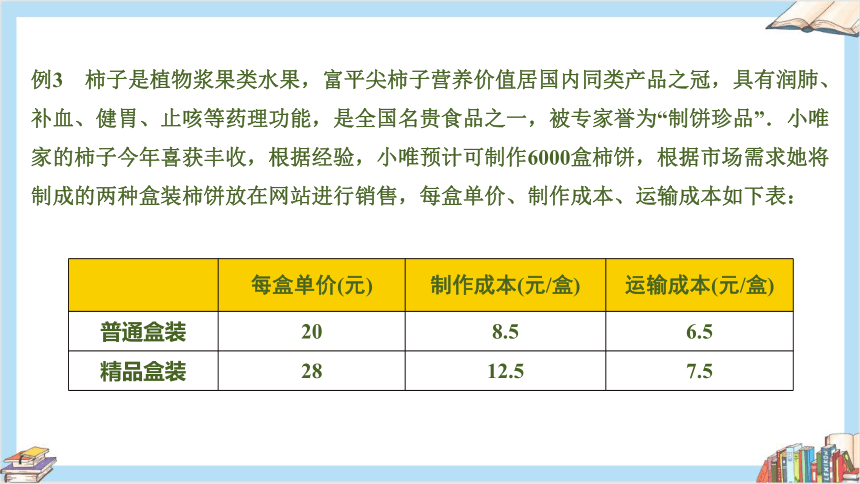
例3 柿子是植物浆果类水果,富平尖柿子营养价值居国内同类产品之冠,具有润肺、补血、健胃、止咳等药理功能,是全国名贵食品之一,被专家誉为“制饼珍品”.小唯家的柿子今年喜获丰收,根据经验,小唯预计可制作6000盒柿饼,根据市场需求她将制成的两种盒装柿饼放在网站进行销售,每盒单价、制作成本、运输成本如下表:
每盒单价(元) 制作成本(元/盒) 运输成本(元/盒)
普通盒装 20 8.5 6.5
精品盒装 28 12.5 7.5
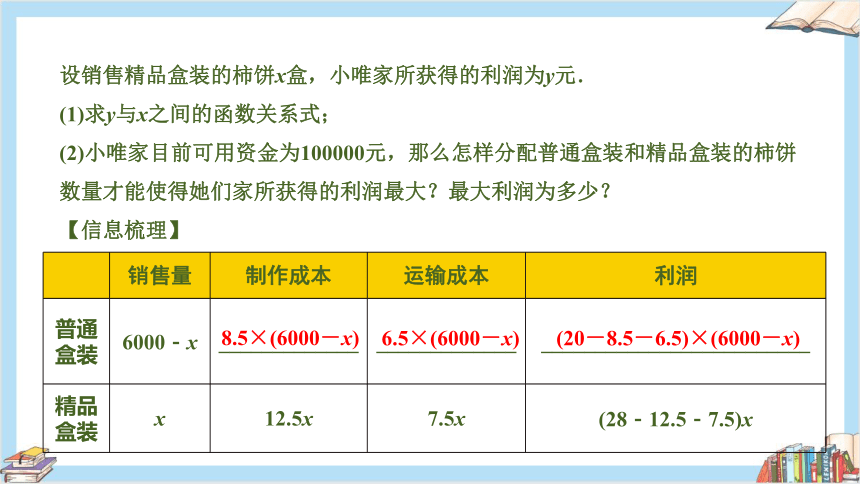
设销售精品盒装的柿饼x盒,小唯家所获得的利润为y元.
(1)求y与x之间的函数关系式;
(2)小唯家目前可用资金为100000元,那么怎样分配普通盒装和精品盒装的柿饼数量才能使得她们家所获得的利润最大?最大利润为多少?
【信息梳理】
销售量 制作成本 运输成本 利润
普通盒装 6000-x _____________ _____________ _________________________
精品盒装 x 12.5x 7.5x (28-12.5-7.5)x
8.5×(6000-x)
6.5×(6000-x)
(20-8.5-6.5)×(6000-x)
【自主解答】
解:(1)根据题意可得:y=(28-12.5-7.5)x+(20-8.5-6.5)×(6000-x)
=3x+30000;
(2)∵可用资金为100000元,
∴(12.5+7.5)x+(8.5+6.5)(6000-x)≤100000,解得:x≤2000,
∵在y=3x+30000中,3>0, ∴y随x的增大而增大,
∴当x=2000时,小唯家所获得的利润最大,最大利润为3×2000+30000=36000,
此时6000-2000=4000(盒),
答:制作普通盒装4000盒,精品盒装2000盒时小唯家获得利润最大,最大利润为36000元.
5年真题、副题“明”考法
类型一 文字型(5年2考)
1. (2021陕西21题7分)根据记录,从地面向上11 km以内,每升高1 km,气温降低6℃;又知道在距地面11 km以上的高空,气温几乎不变.若地面气温为m(℃),设距地面的高度为x(km)处的气温为y(℃).
(1)写出距地面的高度在11 km以内的y与x之间的函数表达式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为-26℃时,飞机距地面的高度为7 km,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距地面12 km的高空,飞机外的气温是多少度呢?请求出假如当时飞机距地面12 km时,飞机外的气温.
解:(1)y=m-6x;(3分)
(2)将x=7,y=-26代入y=m-6x,
得-26=m-42,
∴m=16.
∴当时地面气温为16℃.(5分)
∵x=12>11,
∴y=16-6×11=-50.
∴假如当时飞机距地面12 km时,飞机外的气温为-50℃.(7分)
2. (2021玉门副题21题7分)常温下,有一种烧水壶加热1.5升的纯净水时,加热中的水温y(℃)与加热时间x(秒)之间近似地满足一次函数关系.经实验可知,在常温下用这种壶将1.5升的纯净水加热到70 ℃时,所用时间为3分16秒,再加热40秒,水温正好达到80 ℃.
(1)求出y与x之间的函数关系式;
(2)在常温下,若用这种烧水壶将1.5升的28 ℃纯净水烧开(温度为100 ℃),则需加热多长时间?
解:(1)3分16秒=196秒,196+40=236秒.
设y=kx+b(k≠0),则(196,70)、(236,80)在直线y=kx+b上.
∴y=0.25x+21;(4分)
(2)令y=100,得0.25x+21=100,解得x=316.
令y=28,得0.25x+21=28,解得x=28.
而316-28=288秒=4分48秒.
∴需加热4分48秒.(7分)
3. (2021绥化21题7分)胡老师计划组织朋友暑假去革命圣地延安两日游.经了解,现有甲、乙两家旅行社比较合适,报价均为每人640元,且提供的服务完全相同.针对组团两日游的游客,甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按七五折收费.假设组团参加甲、乙两家旅行社两日游的人数均为x人.
(1)请分别写出甲、乙两家旅行社收取组团两日游的总费用y(元)与x(人)之间的函数关系式;
(2)若胡老师组团参加两日游的人数共有32人,请你通过计算,在甲、乙两家旅行社中,帮助胡老师选择收取总费用较少的一家.
解:(1)甲旅行社:y=640×0.85x=544x,(1分)
乙旅行社:当0≤x≤20时,y=640×0.9x=576x;
当x>20时,y=640×0.9×20+640×0.75(x-20)=480x+1920,
(2)甲旅行社:当x=32时,y=544×32=17408,
乙旅行社:当x=32时,y=480×32+1920=17280,
∵17408>17280,
∴胡老师应选择乙旅行社.(7分)
类型二 图象型(2016.21)
4. (2021十堰副题21题7分)在所挂物体质量不超过25 kg时,一弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数,其图象如图所示.
(1)求y与x之间的函数表达式及该弹簧不挂物体时的长度;
(2)若该弹簧挂上一个物体后,弹簧长度为16 cm,求这个物体的质量.
第4题图
解:(1)设y与x的函数关系式为y=kx+b(k≠0),
∴该弹簧不挂物体时的长度为15 cm.(5分)
(2)当y=16时,16= x+15.解之,得x=5.
∴这个物体的质量为5 kg.(7分)
5. (2021孝感21题7分)昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回.如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.
根据下面图象,回答下列问题:
(1)求线段AB所表示的函数关系式;
(2)已知昨天下午3点时,小明距西安112千米,求他何时到家?
第5题图
解:(1)设线段AB所表示的函数关系式为y=kx+b(k≠0),由题图得A(0,192),B(2,0),代入,
∴线段AB所表示的函数关系式为y=-96x+192(0≤x≤2);(3分)
(2)由题意可知,下午3点时,x=8,y=112.
设线段CD所表示的函数关系式为y=k′x+b′(k′≠0),
解得
∴线段CD所表示的函数关系式为y=80x-528,(5分)
∴当y=192时,80x-528=192,
解得x=9,(6分)
∴他当天下午4点到家.(7分)
6. (2018陕西副题21题7分)一天,小华爸爸开车带全家到西安游玩,实现爷爷、奶奶想看大雁塔,游大唐芙蓉园的愿望,由导航可知,从小华家到西安大雁塔的路程为370 km ,他们全家早上7:00从家出发,途中,他们在一个服务区短暂休息之后,继续行驶,在上午10:00时,他们距离西安大雁塔还有175 km.下图是他们从家到西安大雁塔的过程中,行驶路程y(km)与所用时间x(h)之间的函数图象.请根据相关信息,解答下列问题:
(1)求小华一家在服务区休息了多长时间?
(2)求BC所在直线的函数表达式,并求小
华一家这天几点到达西安大雁塔?
第6题图
解:(1)∵2.5-2=0.5,
∴小华一家在服务区休息了半个小时;(回答“30分钟”也正确)(2分)
(2)设BC所在直线的函数表达式为y=kx+b,
∴y=70x-15.(5分)
令y=370,则70x-15=370.
∴x=5.5. ∴7+5.5=12.5.
∴小华一家这天中午12∶30到达西安大雁塔.(回答“中午12点半”也正确)(7分)
类型三 表格型(5年2考)
7. (2020陕西副题21题7分)某樱桃种植户有20吨樱桃待售,现有两种销售方式:一是批发,二是零售.经过市场调查,这两种销售方式对这个种植户而言,每天的销量及每吨所获的利润如下表:
销售方式 每天销量(吨) 每吨所获利润(元)
批发 3 4000
零售 1 6000
假设该种植户售完20吨樱桃,共批发了x吨,所获总利润为y元.
(1)求出y与x之间的函数关系式;
(2)若受客观因素影响,这个种植户每天只能采用一种销售方式销售,且正好10天销售完所有樱桃,请计算该种植户所获总利润是多少元?
解:(1)由题意得y=4000x+6000×(20-x)=-2000x+120000,
∴y=-2000x+120000(0≤x≤20);(3分)
(2)由题意知
解得x=15,(5分)
∴当x=15时,y=-2000×15+120000=90000(元).
∴该种植户所获总利润为90000元.(7分)
8. (2021庆阳21题7分)在精准扶贫中,某村的李师傅在县政府的扶持下,去年下半年,他对家里的3个温室大棚进行整修改造,然后,1个大棚种植香瓜,另外2个大棚种植甜瓜.今年上半年喜获丰收,现在他家的甜瓜和香瓜已全部售完,他高兴地说:“我的日子终于好了”.
最近,李师傅在扶贫工作者的指导下,计划在农业合作社承包5个大棚,以后就用8个大棚继续种植香瓜和甜瓜.他根据种植经验及今年上半年的市场情况,打算下半年种植时,两个品种同时种,一个大棚只种一个品种的瓜,并预测明年两种瓜的产量、销售价格及成本如下:
项目品种 产量(斤/每棚) 销售价(元/每斤) 成本(元/每棚)
香瓜 2000 12 8000
甜瓜 4500 3 5000
现假设李师傅今年下半年香瓜种植的大棚数为x个,明年上半年8个大棚中所产的瓜全部售完后,获得的利润为y元.
根据以上提供的信息,请你解答下列问题:
(1)求出y与x之间的函数关系式;
(2)求出李师傅种植的8个大棚中,香瓜至少种植几个大棚?才能使获得的利润不低于10万元.
(1) 解:由题意得y=(2000×12-8000)x+(4500×3-5000)(8-x)
=7500x+68000,
∴y=7500x+68000(0<x<8);(4分)
(2)由题意可知7500x+68000≥100000,
∴李师傅种植的8个大棚中至少有5个大棚种植香瓜,才能使获得的利润不低于10万元.(7分)
9. (2021襄阳21题7分)经过一年多的精准帮扶、小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国.小明家网店中红枣和小米这两种商品的相关信息如下表:
商品 红枣 小米
规格 1 kg/袋 2 kg/袋
成本(元/袋) 40 38
售价(元/袋) 60 54
根据上表提供的信息,解答下列问题:
(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共3000 kg,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;
(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000 kg,其中,这种规格的红枣的销售量不低于600 kg,假设这后五个月,销售这种规格的红枣为x(kg),销售这种规格的红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.
解:(1)设前五个月小明家网店销售这种规格的红枣a袋,小米b袋,根据题意,得
∴这前五个月小明家网店销售这种规格的红枣1500袋; (3分)
(2)后五个月小明家网店销售这种规格的红枣x kg,则销售小米(2000-x)kg,
由题意,得y=20x+
=20x+16000-8x=12x+16000(x≥600),(5分)
在y=12x+16000中,
∵k=12>0, ∴y的值随x的值增大而增大,
∵x≥600, ∴当x=600时,y有最小值,
y最小值=12×600+16000=23200,
∴这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润23200元. (7分)
点击链接至练习册
第三单元 函 数
第11课时 一次函数的实际应用
(每年第21题必考,7分)
目
录
典例“串”考点
1
2
5年真题、副题“明”考法
典例“串”考点
例1 碑林书法社小组用的书法练习纸(毛边纸)可以到甲商店购买,也可以到乙商店购买.已知两商店的标价都是每刀20元(每刀100张).甲商店的优惠条件是:若购买不超过10刀,则按标价卖,购买10刀以上,从第11刀开始按标价的七折卖;乙商店的优惠条件是:从第1刀开始按标价的八五折卖.设购买刀数为x(刀),在甲商店购买所需费用为y1元,在乙商店购买所需费用为y2元.
(1)写出y1,y2与x(x>0)之间的函数关系式;
(2)碑林书法社小组现有480元,最多可以买多少刀书法练习纸?
【信息梳理】
商店 购买刀数x(刀) 单价(元) 总费用y(元)
甲 0<x≤10 20 20x
x>10 10以内(包括10):20 10以上:20×0.7 ____
乙 x 20×0.85 ________
20×10+20×0.7×(x-10)
20×0.85x
(2)若在甲商店购买:则14x+60=480,解得x=30,
【自主解答】
例2 五一期间,甲、乙两人分别骑自行车和摩托车从A地出发前往B地郊游,并以各自的速度匀速行驶,到达目的地停止,途中乙休息了一段时间,然后又继续赶路.甲、乙两人各自行驶的路程y(km)与所用时间x(min)之间的函数图象如图所示.
(1)求乙休息后所行的路程y与x之间的函数关系式,并写出自变量x的取值范围;
(2)为了保证及时联络,甲、乙两人在第一次相遇时约定此后两人之间的距离不超过3 km,甲、乙两人是否遵守约定,并说明理由.
例2题图
【思维教练】(1)由图可知,A、B两地之间的距离为________km,甲骑自行车的速度是________km/min.乙休息后所行的路程y与x之间的函数图象经过的点为________和________;
(2)结合题图可知,求出乙开始休息时两人距离及乙刚到达B地时两人的距离,即可判断两人是否遵守约定.
【自主解答】
30
0.25
(50,10)
(80,20)
解:(1)由图可知,A、B两地相距30 km,甲骑自行车的速度为 =0.25 km/min,当甲出发80 min时,距离A地20 km,两人相遇.
设乙休息后所行的路程y与x之间的函数关系为y=kx+b(k≠0),
∵函数图象经过(50,10)和(80,20)两点,
当y=30时,x=110,
∴自变量x的取值范围为:50≤x≤110;
(2)当x=50时,甲行驶了50×0.25=12.5 km,
此时甲、乙之间的距离为12.5-10=2.5<3,遵守约定;
当x=110时,甲行驶了110×0.25=27.5 km,
此时乙到达B地,甲、乙之间的距离为30-27.5=2.5<3,遵守约定.
∴甲、乙两人遵守约定.
例3 柿子是植物浆果类水果,富平尖柿子营养价值居国内同类产品之冠,具有润肺、补血、健胃、止咳等药理功能,是全国名贵食品之一,被专家誉为“制饼珍品”.小唯家的柿子今年喜获丰收,根据经验,小唯预计可制作6000盒柿饼,根据市场需求她将制成的两种盒装柿饼放在网站进行销售,每盒单价、制作成本、运输成本如下表:
每盒单价(元) 制作成本(元/盒) 运输成本(元/盒)
普通盒装 20 8.5 6.5
精品盒装 28 12.5 7.5
设销售精品盒装的柿饼x盒,小唯家所获得的利润为y元.
(1)求y与x之间的函数关系式;
(2)小唯家目前可用资金为100000元,那么怎样分配普通盒装和精品盒装的柿饼数量才能使得她们家所获得的利润最大?最大利润为多少?
【信息梳理】
销售量 制作成本 运输成本 利润
普通盒装 6000-x _____________ _____________ _________________________
精品盒装 x 12.5x 7.5x (28-12.5-7.5)x
8.5×(6000-x)
6.5×(6000-x)
(20-8.5-6.5)×(6000-x)
【自主解答】
解:(1)根据题意可得:y=(28-12.5-7.5)x+(20-8.5-6.5)×(6000-x)
=3x+30000;
(2)∵可用资金为100000元,
∴(12.5+7.5)x+(8.5+6.5)(6000-x)≤100000,解得:x≤2000,
∵在y=3x+30000中,3>0, ∴y随x的增大而增大,
∴当x=2000时,小唯家所获得的利润最大,最大利润为3×2000+30000=36000,
此时6000-2000=4000(盒),
答:制作普通盒装4000盒,精品盒装2000盒时小唯家获得利润最大,最大利润为36000元.
5年真题、副题“明”考法
类型一 文字型(5年2考)
1. (2021陕西21题7分)根据记录,从地面向上11 km以内,每升高1 km,气温降低6℃;又知道在距地面11 km以上的高空,气温几乎不变.若地面气温为m(℃),设距地面的高度为x(km)处的气温为y(℃).
(1)写出距地面的高度在11 km以内的y与x之间的函数表达式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为-26℃时,飞机距地面的高度为7 km,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距地面12 km的高空,飞机外的气温是多少度呢?请求出假如当时飞机距地面12 km时,飞机外的气温.
解:(1)y=m-6x;(3分)
(2)将x=7,y=-26代入y=m-6x,
得-26=m-42,
∴m=16.
∴当时地面气温为16℃.(5分)
∵x=12>11,
∴y=16-6×11=-50.
∴假如当时飞机距地面12 km时,飞机外的气温为-50℃.(7分)
2. (2021玉门副题21题7分)常温下,有一种烧水壶加热1.5升的纯净水时,加热中的水温y(℃)与加热时间x(秒)之间近似地满足一次函数关系.经实验可知,在常温下用这种壶将1.5升的纯净水加热到70 ℃时,所用时间为3分16秒,再加热40秒,水温正好达到80 ℃.
(1)求出y与x之间的函数关系式;
(2)在常温下,若用这种烧水壶将1.5升的28 ℃纯净水烧开(温度为100 ℃),则需加热多长时间?
解:(1)3分16秒=196秒,196+40=236秒.
设y=kx+b(k≠0),则(196,70)、(236,80)在直线y=kx+b上.
∴y=0.25x+21;(4分)
(2)令y=100,得0.25x+21=100,解得x=316.
令y=28,得0.25x+21=28,解得x=28.
而316-28=288秒=4分48秒.
∴需加热4分48秒.(7分)
3. (2021绥化21题7分)胡老师计划组织朋友暑假去革命圣地延安两日游.经了解,现有甲、乙两家旅行社比较合适,报价均为每人640元,且提供的服务完全相同.针对组团两日游的游客,甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按七五折收费.假设组团参加甲、乙两家旅行社两日游的人数均为x人.
(1)请分别写出甲、乙两家旅行社收取组团两日游的总费用y(元)与x(人)之间的函数关系式;
(2)若胡老师组团参加两日游的人数共有32人,请你通过计算,在甲、乙两家旅行社中,帮助胡老师选择收取总费用较少的一家.
解:(1)甲旅行社:y=640×0.85x=544x,(1分)
乙旅行社:当0≤x≤20时,y=640×0.9x=576x;
当x>20时,y=640×0.9×20+640×0.75(x-20)=480x+1920,
(2)甲旅行社:当x=32时,y=544×32=17408,
乙旅行社:当x=32时,y=480×32+1920=17280,
∵17408>17280,
∴胡老师应选择乙旅行社.(7分)
类型二 图象型(2016.21)
4. (2021十堰副题21题7分)在所挂物体质量不超过25 kg时,一弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数,其图象如图所示.
(1)求y与x之间的函数表达式及该弹簧不挂物体时的长度;
(2)若该弹簧挂上一个物体后,弹簧长度为16 cm,求这个物体的质量.
第4题图
解:(1)设y与x的函数关系式为y=kx+b(k≠0),
∴该弹簧不挂物体时的长度为15 cm.(5分)
(2)当y=16时,16= x+15.解之,得x=5.
∴这个物体的质量为5 kg.(7分)
5. (2021孝感21题7分)昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回.如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.
根据下面图象,回答下列问题:
(1)求线段AB所表示的函数关系式;
(2)已知昨天下午3点时,小明距西安112千米,求他何时到家?
第5题图
解:(1)设线段AB所表示的函数关系式为y=kx+b(k≠0),由题图得A(0,192),B(2,0),代入,
∴线段AB所表示的函数关系式为y=-96x+192(0≤x≤2);(3分)
(2)由题意可知,下午3点时,x=8,y=112.
设线段CD所表示的函数关系式为y=k′x+b′(k′≠0),
解得
∴线段CD所表示的函数关系式为y=80x-528,(5分)
∴当y=192时,80x-528=192,
解得x=9,(6分)
∴他当天下午4点到家.(7分)
6. (2018陕西副题21题7分)一天,小华爸爸开车带全家到西安游玩,实现爷爷、奶奶想看大雁塔,游大唐芙蓉园的愿望,由导航可知,从小华家到西安大雁塔的路程为370 km ,他们全家早上7:00从家出发,途中,他们在一个服务区短暂休息之后,继续行驶,在上午10:00时,他们距离西安大雁塔还有175 km.下图是他们从家到西安大雁塔的过程中,行驶路程y(km)与所用时间x(h)之间的函数图象.请根据相关信息,解答下列问题:
(1)求小华一家在服务区休息了多长时间?
(2)求BC所在直线的函数表达式,并求小
华一家这天几点到达西安大雁塔?
第6题图
解:(1)∵2.5-2=0.5,
∴小华一家在服务区休息了半个小时;(回答“30分钟”也正确)(2分)
(2)设BC所在直线的函数表达式为y=kx+b,
∴y=70x-15.(5分)
令y=370,则70x-15=370.
∴x=5.5. ∴7+5.5=12.5.
∴小华一家这天中午12∶30到达西安大雁塔.(回答“中午12点半”也正确)(7分)
类型三 表格型(5年2考)
7. (2020陕西副题21题7分)某樱桃种植户有20吨樱桃待售,现有两种销售方式:一是批发,二是零售.经过市场调查,这两种销售方式对这个种植户而言,每天的销量及每吨所获的利润如下表:
销售方式 每天销量(吨) 每吨所获利润(元)
批发 3 4000
零售 1 6000
假设该种植户售完20吨樱桃,共批发了x吨,所获总利润为y元.
(1)求出y与x之间的函数关系式;
(2)若受客观因素影响,这个种植户每天只能采用一种销售方式销售,且正好10天销售完所有樱桃,请计算该种植户所获总利润是多少元?
解:(1)由题意得y=4000x+6000×(20-x)=-2000x+120000,
∴y=-2000x+120000(0≤x≤20);(3分)
(2)由题意知
解得x=15,(5分)
∴当x=15时,y=-2000×15+120000=90000(元).
∴该种植户所获总利润为90000元.(7分)
8. (2021庆阳21题7分)在精准扶贫中,某村的李师傅在县政府的扶持下,去年下半年,他对家里的3个温室大棚进行整修改造,然后,1个大棚种植香瓜,另外2个大棚种植甜瓜.今年上半年喜获丰收,现在他家的甜瓜和香瓜已全部售完,他高兴地说:“我的日子终于好了”.
最近,李师傅在扶贫工作者的指导下,计划在农业合作社承包5个大棚,以后就用8个大棚继续种植香瓜和甜瓜.他根据种植经验及今年上半年的市场情况,打算下半年种植时,两个品种同时种,一个大棚只种一个品种的瓜,并预测明年两种瓜的产量、销售价格及成本如下:
项目品种 产量(斤/每棚) 销售价(元/每斤) 成本(元/每棚)
香瓜 2000 12 8000
甜瓜 4500 3 5000
现假设李师傅今年下半年香瓜种植的大棚数为x个,明年上半年8个大棚中所产的瓜全部售完后,获得的利润为y元.
根据以上提供的信息,请你解答下列问题:
(1)求出y与x之间的函数关系式;
(2)求出李师傅种植的8个大棚中,香瓜至少种植几个大棚?才能使获得的利润不低于10万元.
(1) 解:由题意得y=(2000×12-8000)x+(4500×3-5000)(8-x)
=7500x+68000,
∴y=7500x+68000(0<x<8);(4分)
(2)由题意可知7500x+68000≥100000,
∴李师傅种植的8个大棚中至少有5个大棚种植香瓜,才能使获得的利润不低于10万元.(7分)
9. (2021襄阳21题7分)经过一年多的精准帮扶、小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国.小明家网店中红枣和小米这两种商品的相关信息如下表:
商品 红枣 小米
规格 1 kg/袋 2 kg/袋
成本(元/袋) 40 38
售价(元/袋) 60 54
根据上表提供的信息,解答下列问题:
(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共3000 kg,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;
(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000 kg,其中,这种规格的红枣的销售量不低于600 kg,假设这后五个月,销售这种规格的红枣为x(kg),销售这种规格的红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.
解:(1)设前五个月小明家网店销售这种规格的红枣a袋,小米b袋,根据题意,得
∴这前五个月小明家网店销售这种规格的红枣1500袋; (3分)
(2)后五个月小明家网店销售这种规格的红枣x kg,则销售小米(2000-x)kg,
由题意,得y=20x+
=20x+16000-8x=12x+16000(x≥600),(5分)
在y=12x+16000中,
∵k=12>0, ∴y的值随x的值增大而增大,
∵x≥600, ∴当x=600时,y有最小值,
y最小值=12×600+16000=23200,
∴这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润23200元. (7分)
点击链接至练习册
同课章节目录
