10.2.2 复数的乘法与除法 课件(共34张PPT)
文档属性
| 名称 | 10.2.2 复数的乘法与除法 课件(共34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 00:00:00 | ||
图片预览









文档简介
第十章 复 数
已知两个复数z1=a+bi, z2=c+di(a,b,c,d是实数)
即:两个复数相加(减)就是
实部与实部,虚部与虚部分别相加(减).
(1)加法法则:z1+z2=(a+bi)+(c+di)=(a+c)+(c+d)i.
(2)减法法则:z1-z2=(a+bi)-(c+di) =(a-c)+(b-d)i.
(a+bi)±(c+di) =(a±c)+(b±d)i
x
o
y
z1(a,b)
z2(c,d)
z(a+c,b+d)
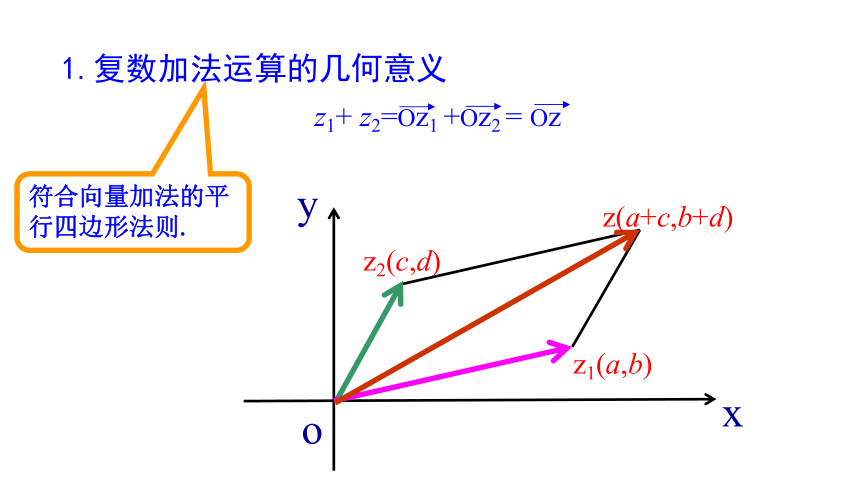
z1+ z2=Oz1 +Oz2 = Oz
符合向量加法的平行四边形法则.
1.复数加法运算的几何意义
x
o
y
z1(a,b)
z2(c,d)
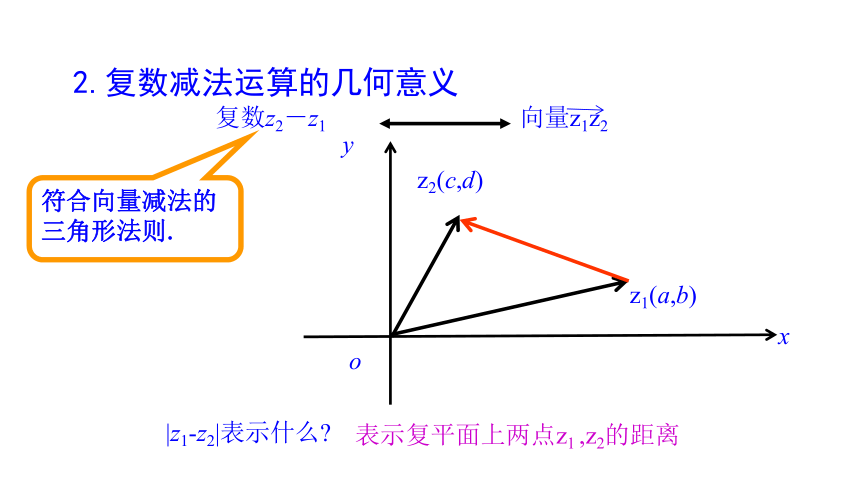
复数z2-z1
向量z1z2
符合向量减法的三角形法则.
2.复数减法运算的几何意义
|z1-z2|表示什么?
表示复平面上两点z1 ,z2的距离
复平面中点
Z1与点Z2间的距离
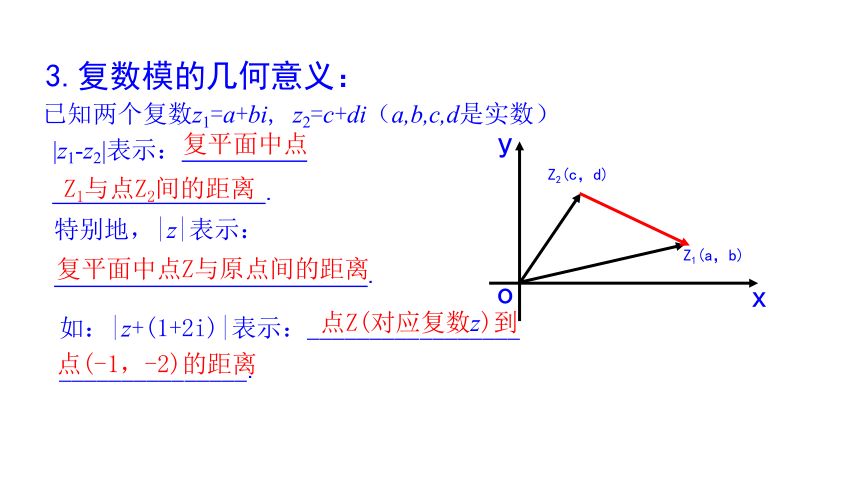
|z1-z2|表示:__________
_________________.
已知两个复数z1=a+bi, z2=c+di(a,b,c,d是实数)
3.复数模的几何意义:
Z1(a,b)
o
x
y
Z2(c,d)
特别地,|z|表示:
________________________.
复平面中点Z与原点间的距离
如:|z+(1+2i)|表示:_________________
_______________.
点(-1,-2)的距离
点Z(对应复数z)到
1.掌握复数的代数形式的乘法与除法运算法则.2.对复数除法法则的运用.3.乘法的运算法则与运算律.4.共轭复数的定义是什么.
1.数学抽象:复数乘法、除法运算法则;2.逻辑推理:复数乘法运算律的推导;3.数学运算:复数四则运算; 4.数学建模:结合实数范围内求根公式和复数四则运算,解决复数范围内的方程根问题.
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
复数的乘法
尝试与发现
问题2:复数的正整数指数幂
D
C
先写成分式的形式
然后分母实数化,分子分母同时乘以分母的共轭复数
结果化简成代数形式
A
2
归纳总结
尝试与发现
实系数一元二次方程在复数范围内的解集
典例解析
互为共轭
归纳总结
当堂达标
A
B
2
1. 复数的乘法运算
2. 复数乘法的运算律
3. 复数的除法法则
复数的乘除运算
1. 复数乘法与实数多项式乘法类似,在计算两个复数的乘积时,先按照多项
式的乘法展开,再将i2换成-1,最后合并同类项即可.
2.根据复数的除法法则,通过分子、分母都乘分母的共轭复数,使“分母实数化”,这个过程与“分母有理化”类似.
与复数有关的方程问题,一般是利用复数相等的充要条件,把复数问题实数化进行求解,根与系数的关系仍适用,但判别式“Δ”不再适用.
1.数学抽象:复数乘法、除法运算法则;
2.逻辑推理:复数乘法运算律的推导;
3.数学运算:复数四则运算;
4.数学建模:结合实数范围内求根公式和复数四则运算,解决复数范围内的方程根问题.
方法总结
易错提醒
核心知识
D
D
3
4.已知方程x2-2x+2=0有两虚根为x1, x2, 求x14+x24的值.
注:在复数范围内方程的根与系数的关系仍适用.
男儿不展风云志,空负天生八尺躯.
已知两个复数z1=a+bi, z2=c+di(a,b,c,d是实数)
即:两个复数相加(减)就是
实部与实部,虚部与虚部分别相加(减).
(1)加法法则:z1+z2=(a+bi)+(c+di)=(a+c)+(c+d)i.
(2)减法法则:z1-z2=(a+bi)-(c+di) =(a-c)+(b-d)i.
(a+bi)±(c+di) =(a±c)+(b±d)i
x
o
y
z1(a,b)
z2(c,d)
z(a+c,b+d)
z1+ z2=Oz1 +Oz2 = Oz
符合向量加法的平行四边形法则.
1.复数加法运算的几何意义
x
o
y
z1(a,b)
z2(c,d)
复数z2-z1
向量z1z2
符合向量减法的三角形法则.
2.复数减法运算的几何意义
|z1-z2|表示什么?
表示复平面上两点z1 ,z2的距离
复平面中点
Z1与点Z2间的距离
|z1-z2|表示:__________
_________________.
已知两个复数z1=a+bi, z2=c+di(a,b,c,d是实数)
3.复数模的几何意义:
Z1(a,b)
o
x
y
Z2(c,d)
特别地,|z|表示:
________________________.
复平面中点Z与原点间的距离
如:|z+(1+2i)|表示:_________________
_______________.
点(-1,-2)的距离
点Z(对应复数z)到
1.掌握复数的代数形式的乘法与除法运算法则.2.对复数除法法则的运用.3.乘法的运算法则与运算律.4.共轭复数的定义是什么.
1.数学抽象:复数乘法、除法运算法则;2.逻辑推理:复数乘法运算律的推导;3.数学运算:复数四则运算; 4.数学建模:结合实数范围内求根公式和复数四则运算,解决复数范围内的方程根问题.
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
复数的乘法
尝试与发现
问题2:复数的正整数指数幂
D
C
先写成分式的形式
然后分母实数化,分子分母同时乘以分母的共轭复数
结果化简成代数形式
A
2
归纳总结
尝试与发现
实系数一元二次方程在复数范围内的解集
典例解析
互为共轭
归纳总结
当堂达标
A
B
2
1. 复数的乘法运算
2. 复数乘法的运算律
3. 复数的除法法则
复数的乘除运算
1. 复数乘法与实数多项式乘法类似,在计算两个复数的乘积时,先按照多项
式的乘法展开,再将i2换成-1,最后合并同类项即可.
2.根据复数的除法法则,通过分子、分母都乘分母的共轭复数,使“分母实数化”,这个过程与“分母有理化”类似.
与复数有关的方程问题,一般是利用复数相等的充要条件,把复数问题实数化进行求解,根与系数的关系仍适用,但判别式“Δ”不再适用.
1.数学抽象:复数乘法、除法运算法则;
2.逻辑推理:复数乘法运算律的推导;
3.数学运算:复数四则运算;
4.数学建模:结合实数范围内求根公式和复数四则运算,解决复数范围内的方程根问题.
方法总结
易错提醒
核心知识
D
D
3
4.已知方程x2-2x+2=0有两虚根为x1, x2, 求x14+x24的值.
注:在复数范围内方程的根与系数的关系仍适用.
男儿不展风云志,空负天生八尺躯.
