11.1.5 旋转体 课件(共38张PPT)
文档属性
| 名称 | 11.1.5 旋转体 课件(共38张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 12:59:23 | ||
图片预览









文档简介
11.1.5旋转体
1.掌握圆柱、圆锥、圆台和球的结构特征. 2.理解柱、锥、台的关系.3.会用柱、锥、台、球的结构特征描述简单组合体.4.能运用简单组合体的结构特征描述现实生活中的实际模型.
1.数学抽象:圆柱、圆锥、圆台、球的定义;2.逻辑推理:圆柱、圆锥、圆台、球的结构特征;3.数学运算:旋转体的母线、底面圆半径、球的相关计算;4.直观想象:简单组合体的结构特征。
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
问题1:圆柱、圆锥、圆台
答:圆台可以看成平行于圆锥底面的平面截圆锥所得到的几何体.
例1.写出圆台中任意两条母线的位置关系,任意一条母线与底面的位置关系,以及两个底面的位置关系。
解:圆台中任意两条母线都相交,任意一条母线与底面都相交,两个底面相互平行.
答案:B 圆柱的母线长与高 相等,则其高等于10.
B
问题2:圆柱、圆锥、圆台的侧面积、表面积
知识点3:圆柱的底面积、侧面积、表面积
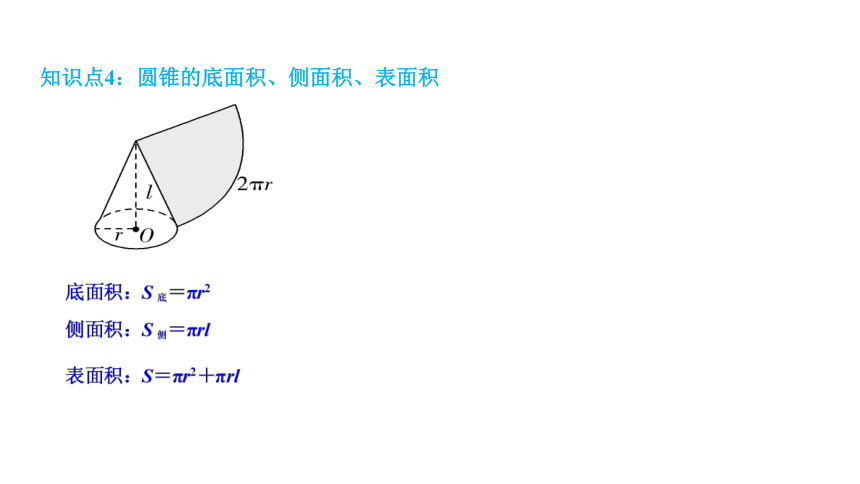
知识点4:圆锥的底面积、侧面积、表面积
知识点5:圆台的底面积、侧面积、表面积
【即时训练】
1.圆柱OO′的底面直径为4,母线长为6,则该圆柱的侧面积为________,表面积为________.
答案 24π 32π
答案 2π
问题3:球
知识点3:球的表示方法
球面可以看成空间中到一个定点的距离等于定长的点的集合.
知识点4:球的截面
【即时训练】
1.球的任意两条直径不一定具有的性质是( )
A.相交 B.平分
C.垂直 D.都经过球心
答案:C 球的任意两条直径不一定垂直.
C
答案:C 命题①是正确的;
命题②是错误的,只有两点的连线段经过球心时才为直径;命题③是错误的,
命题④是正确的,截面为圆面(圆及其内部)而不是圆.
C
知识点5:球的表面积
如果设球的半径为R,那么球的表面积为S=4πR2
【即时训练】
1.直径为6的球的表面积是( )
A.36π B.18π C.144π D.9π
答案:A 球的半径为3,表面积S=4π×32=36π.
A
2.一个球的表面积是16π,则它的半径是( )
A.6 B.8
C.4 D.2
答案:D 设球的半径为R,则由题意可知4πR2=16π,故R=2.所以球的半径为2.
D
例3.已知一个长方体的8个顶点都在一个球面上,且长方体的棱长为3,4,5,求球的表面积.
【变式练习】
1.若棱长为2的正方体的各个顶点均在同一球面上,求此球的表面积.
2. 将条件改为“球与棱长为2的正方体的面都相切”,如何求解?
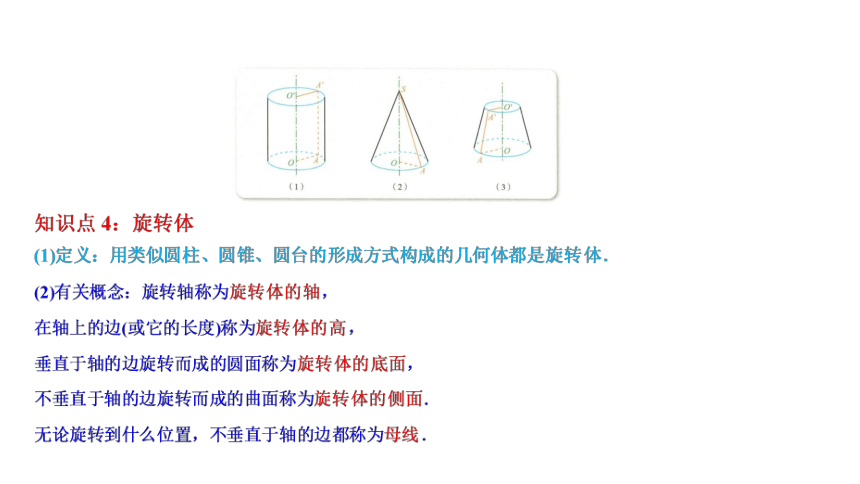
旋转体
几何特征
图形
圆柱
圆锥
1.圆柱、圆锥、圆台和球
以矩形的一边所在的直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱
以直角三角形的一直角边所在的直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥
旋转体
几何特征
图形
圆台
球
用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分,叫做圆台
以半圆的直径所在的直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体
简单几何体的结构特征
柱体
锥体
台体
球
棱柱
圆柱
棱锥
圆锥
棱台
圆台
2.圆柱、圆锥、圆台和球的结构图
简单几何体的分类:
简单几何体
多面体
旋转体
棱柱
棱锥
棱台
圆柱
圆锥
圆台
球
圆柱、圆锥、
圆台、球、简单组合体的结构特征
求圆柱、圆锥、圆台侧面上两点间最短距离都要转化到侧面展开图中,“化曲为直”是求几何体表面上两点间最短距离的好方法.
1.判断简单旋转体结构特征的方法
核心知识
方法总结
易错提醒
核心素养
1.数学抽象:圆柱、圆锥、圆台、球的定义;
2.逻辑推理:圆柱、圆锥、圆台、球的结构特征;
3.数学运算:旋转体的母线、底面圆半径、球的相关计算;
4.直观想象:简单组合体的结构特征。
1.明确由哪个平面图形旋转而成.
2.明确旋转轴是哪条直线.
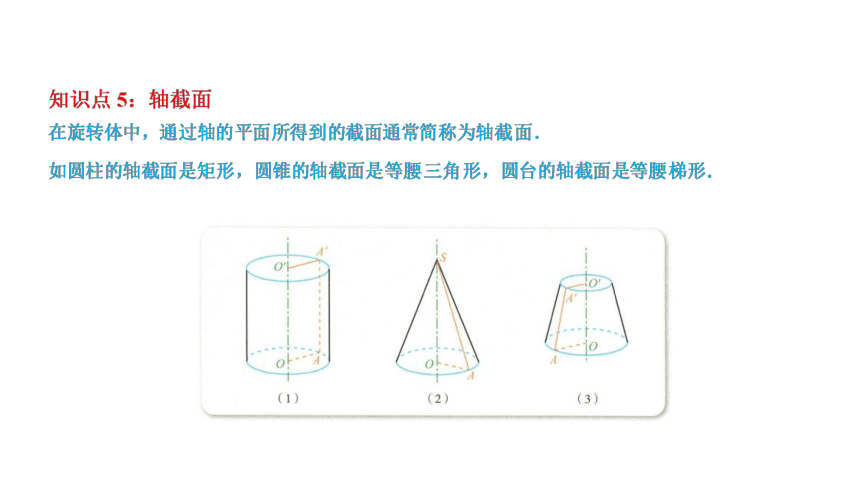
2.旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构
特征的关键量.
1.圆柱: 定义,相关概念
2.圆锥: 定义,相关概念
3.圆台: 定义,相关概念
4.球: 定义,相关概念
A
D
5
解
:
圆锥的轴截面如图所示,由图可知,底面半径
r
=
(
5
2
)
2
-
r
2
.
所以
r
=
5.
4. 一个球内有相距9 cm的两个平行截面,它们的面积分别为49π cm2和
400π cm2,求球的表面积.
解 (1)当截面在球心的同侧时,
如图①所示为球的轴截面,由截面性质知AO1∥BO2,
O1,O2为两截面圆的圆心,且OO1⊥AO1,OO2⊥BO2,
设球的半径为R,
因为π(O2B)2=49π,所以O2B=7 cm,
同理得:O1A=20 cm.
设OO1=x,则OO2=(x+9) cm,
在Rt△O1OA中,R2=x2+202,①
在Rt△OO2B中,R2=72+(x+9)2,②
联立①②可得x=15,R=25.
所以S球=4πR2=2 500π cm2,
故球的表面积为2 500π cm2.
(2)当截面在球心的两侧时,如图②所示为球的轴截面,由球的截面性质知,O1A∥O2B,且O1,O2分别为两截面圆的圆心,则OO1⊥O1A,
不论去往何方,身后永远有不变的祝福,凝注的眼光——母校用宽大的胸怀包容我们,等待我们,期许我们。
1.掌握圆柱、圆锥、圆台和球的结构特征. 2.理解柱、锥、台的关系.3.会用柱、锥、台、球的结构特征描述简单组合体.4.能运用简单组合体的结构特征描述现实生活中的实际模型.
1.数学抽象:圆柱、圆锥、圆台、球的定义;2.逻辑推理:圆柱、圆锥、圆台、球的结构特征;3.数学运算:旋转体的母线、底面圆半径、球的相关计算;4.直观想象:简单组合体的结构特征。
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
问题1:圆柱、圆锥、圆台
答:圆台可以看成平行于圆锥底面的平面截圆锥所得到的几何体.
例1.写出圆台中任意两条母线的位置关系,任意一条母线与底面的位置关系,以及两个底面的位置关系。
解:圆台中任意两条母线都相交,任意一条母线与底面都相交,两个底面相互平行.
答案:B 圆柱的母线长与高 相等,则其高等于10.
B
问题2:圆柱、圆锥、圆台的侧面积、表面积
知识点3:圆柱的底面积、侧面积、表面积
知识点4:圆锥的底面积、侧面积、表面积
知识点5:圆台的底面积、侧面积、表面积
【即时训练】
1.圆柱OO′的底面直径为4,母线长为6,则该圆柱的侧面积为________,表面积为________.
答案 24π 32π
答案 2π
问题3:球
知识点3:球的表示方法
球面可以看成空间中到一个定点的距离等于定长的点的集合.
知识点4:球的截面
【即时训练】
1.球的任意两条直径不一定具有的性质是( )
A.相交 B.平分
C.垂直 D.都经过球心
答案:C 球的任意两条直径不一定垂直.
C
答案:C 命题①是正确的;
命题②是错误的,只有两点的连线段经过球心时才为直径;命题③是错误的,
命题④是正确的,截面为圆面(圆及其内部)而不是圆.
C
知识点5:球的表面积
如果设球的半径为R,那么球的表面积为S=4πR2
【即时训练】
1.直径为6的球的表面积是( )
A.36π B.18π C.144π D.9π
答案:A 球的半径为3,表面积S=4π×32=36π.
A
2.一个球的表面积是16π,则它的半径是( )
A.6 B.8
C.4 D.2
答案:D 设球的半径为R,则由题意可知4πR2=16π,故R=2.所以球的半径为2.
D
例3.已知一个长方体的8个顶点都在一个球面上,且长方体的棱长为3,4,5,求球的表面积.
【变式练习】
1.若棱长为2的正方体的各个顶点均在同一球面上,求此球的表面积.
2. 将条件改为“球与棱长为2的正方体的面都相切”,如何求解?
旋转体
几何特征
图形
圆柱
圆锥
1.圆柱、圆锥、圆台和球
以矩形的一边所在的直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱
以直角三角形的一直角边所在的直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥
旋转体
几何特征
图形
圆台
球
用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分,叫做圆台
以半圆的直径所在的直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体
简单几何体的结构特征
柱体
锥体
台体
球
棱柱
圆柱
棱锥
圆锥
棱台
圆台
2.圆柱、圆锥、圆台和球的结构图
简单几何体的分类:
简单几何体
多面体
旋转体
棱柱
棱锥
棱台
圆柱
圆锥
圆台
球
圆柱、圆锥、
圆台、球、简单组合体的结构特征
求圆柱、圆锥、圆台侧面上两点间最短距离都要转化到侧面展开图中,“化曲为直”是求几何体表面上两点间最短距离的好方法.
1.判断简单旋转体结构特征的方法
核心知识
方法总结
易错提醒
核心素养
1.数学抽象:圆柱、圆锥、圆台、球的定义;
2.逻辑推理:圆柱、圆锥、圆台、球的结构特征;
3.数学运算:旋转体的母线、底面圆半径、球的相关计算;
4.直观想象:简单组合体的结构特征。
1.明确由哪个平面图形旋转而成.
2.明确旋转轴是哪条直线.
2.旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构
特征的关键量.
1.圆柱: 定义,相关概念
2.圆锥: 定义,相关概念
3.圆台: 定义,相关概念
4.球: 定义,相关概念
A
D
5
解
:
圆锥的轴截面如图所示,由图可知,底面半径
r
=
(
5
2
)
2
-
r
2
.
所以
r
=
5.
4. 一个球内有相距9 cm的两个平行截面,它们的面积分别为49π cm2和
400π cm2,求球的表面积.
解 (1)当截面在球心的同侧时,
如图①所示为球的轴截面,由截面性质知AO1∥BO2,
O1,O2为两截面圆的圆心,且OO1⊥AO1,OO2⊥BO2,
设球的半径为R,
因为π(O2B)2=49π,所以O2B=7 cm,
同理得:O1A=20 cm.
设OO1=x,则OO2=(x+9) cm,
在Rt△O1OA中,R2=x2+202,①
在Rt△OO2B中,R2=72+(x+9)2,②
联立①②可得x=15,R=25.
所以S球=4πR2=2 500π cm2,
故球的表面积为2 500π cm2.
(2)当截面在球心的两侧时,如图②所示为球的轴截面,由球的截面性质知,O1A∥O2B,且O1,O2分别为两截面圆的圆心,则OO1⊥O1A,
不论去往何方,身后永远有不变的祝福,凝注的眼光——母校用宽大的胸怀包容我们,等待我们,期许我们。
