11.1.6 祖暅原理与几何体的体积 课件(共33张PPT)
文档属性
| 名称 | 11.1.6 祖暅原理与几何体的体积 课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 00:00:00 | ||
图片预览








文档简介
11.1.6祖暅原理与几何体的体积
引入:
祖暅,字景烁,祖冲之之子,范阳郡蓟县人(今河北省涞源县人),南北朝时代的伟大科学家。祖暅在数学上有突出贡献,他在实践的基础上,于5世纪末提出了体积的计算原理。祖暅原理:“幂势既同,则积不容异”。
“势”即是高,“幂”即是面积。
祖暅原理
祖暅原理的提出要比其他国家的数学家早一千多年。在欧洲直到17世纪,才有意大利数学家卡瓦列里提出上述结论。
祖冲之父子是
我们中华民族的
骄傲和自豪
1.了解祖暅原理.2.能运用公式求棱柱、棱锥、棱台、球体积.3.熟悉棱柱、棱锥、棱台之间的转换关系,培养转化与化归的思想与空间想象能力.
1.数学抽象:棱柱、棱锥、棱台的体积公式;2.数学运算:求多面体体积;3.数学建模:运用棱柱、棱锥、棱台的表面积和体积公式进行计算和解决有关实际问题.
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
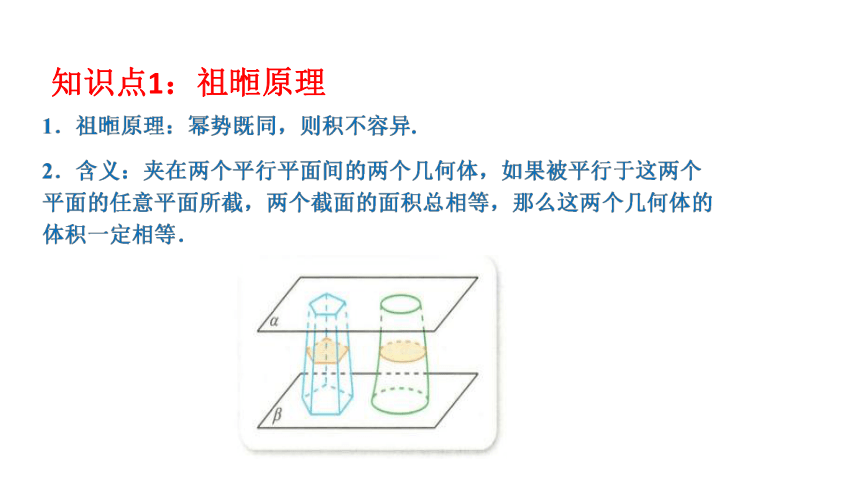
知识点1:祖暅原理
答案:被平行于这两个平面的任意平面所截时,三棱锥和三棱柱不满足两个截面的面积总相等,故这两个几何体的体积不相等.
答案:根据祖暅原理,知三棱柱ABC-A1B1C1与圆柱O′O的体积相等.
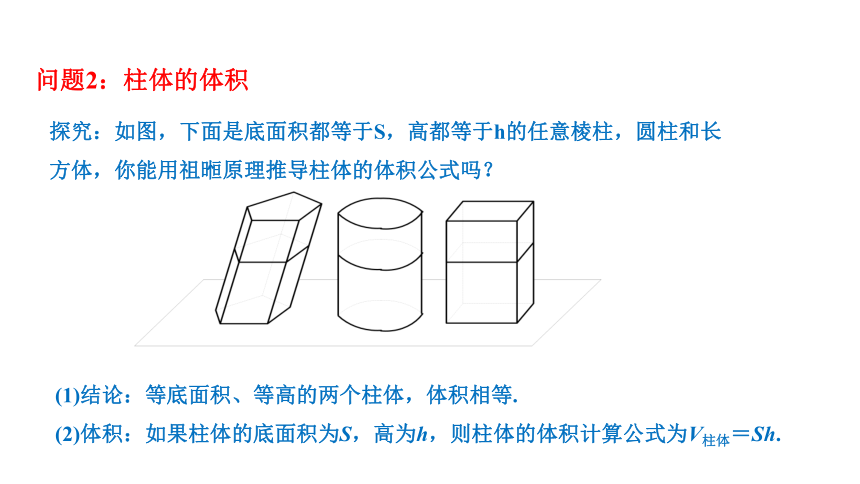
问题2:柱体的体积
探究:如图,下面是底面积都等于S,高都等于h的任意棱柱,圆柱和长方体,你能用祖暅原理推导柱体的体积公式吗?
(1)结论:等底面积、等高的两个柱体,体积相等.
(2)体积:如果柱体的底面积为S,高为h,则柱体的体积计算公式为V柱体=Sh.
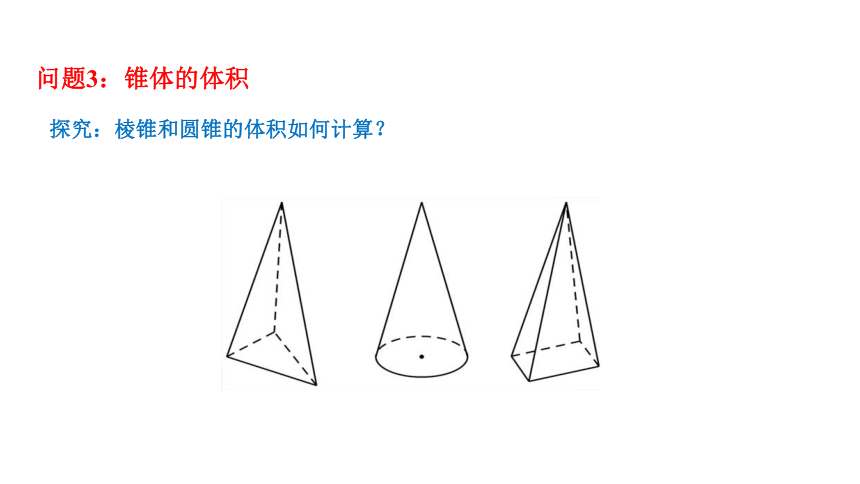
问题3:锥体的体积
探究:棱锥和圆锥的体积如何计算?
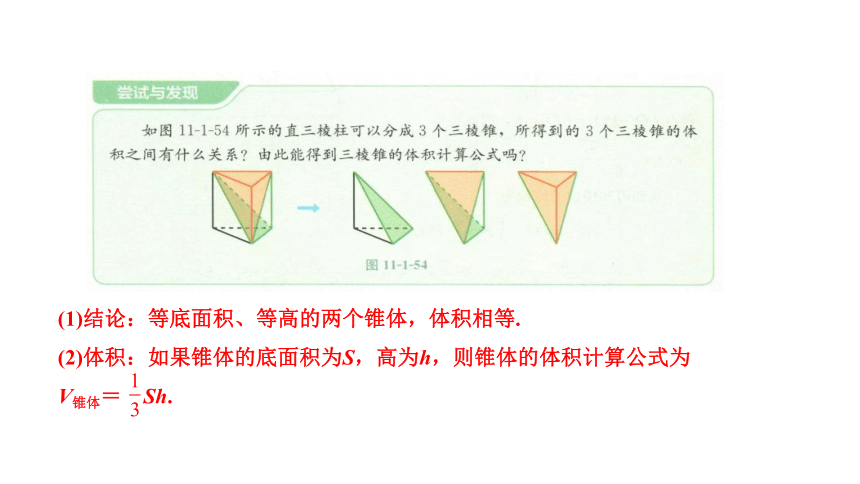
(1)结论:等底面积、等高的两个锥体,体积相等.
(2)体积:如果锥体的底面积为S,高为h,则锥体的体积计算公式为
V锥体= Sh.
【即时训练】
1.圆锥的底面半径为4,母线长为6,则体积为________.
问题4:台体的体积
探究:棱台、圆台的体积如何求解?
因为台体可以看成锥体截去一个小锥体得到,所以台体的体积可以通过计算锥体的体积之差来得到.
【即时训练】
已知棱台的上、下底面面积分别为4,16,高为3,则棱台的体积为________.
28
思考:柱体、锥体、球体的体积有什么关系?
问题5:球的体积
尝试与发现:
(1)你能想办法测出一个乒乓球的体积吗?
(2)如图所示是底面积和高都相等的两个几何体,左边是半球,右边是圆柱被挖去一个倒立的圆锥剩余的部分,用平行于半球与圆柱底面的平面去截这两个几何体,分别指出截面的形状,并讨论两个截面面积的大小关系,由此你能得到球的体积公式吗?
【即时训练】
1.若将球的半径扩大到原来的2倍,则它的体积增大到原来的( )
A.2倍 B.4倍
C.8倍 D.16倍
C
求多面体表面积的方法 1.多面体的表面积转化为各面面积之和.2.解决有关棱台的问题时,常用两种解题思路:一是把基本量转化到梯形中去解决;二是把棱台还原成棱锥,利用棱锥的有关知识来解决.
求几何体体积的方法①公式法:直接代入公式求解.②等积法:只需选用底面积和高都易求的形式即可.③分割法:将几何体分割成易求解的几部分,分别求体积
核心知识
方法总结
易错提醒
核心素养
棱柱、棱锥、棱台的体积
1.数学抽象:棱柱、棱锥、棱台的体积公式;
2.数学运算:求多面体或多面体组合体的表面积和体积;
3.数学建模:运用棱柱、棱锥、棱台的体积公式进行计算和解决有关实际问题.
棱锥
棱台
棱柱
棱柱、棱锥、棱台的体积
祖暅原理
祖暅原理:利用祖暅原理求不规则几何体的体积。
求几何体体积的方法①公式法:直接代入公式求解.②等积法:只需选用底面积和高都易求的形式即可.③分割法:将几何体分割成易求解的几部分分别求体积
柱、锥、台的体积的计算,一般要找出相应的底面和高,要充分利用截面、轴截面,求出所需要的量,最后代入公式计算.
1.正方体的表面积为96,则正方体的体积为( )
A.48 B.64 C.16 D.96
B
2.(1)过长方体的一个顶点的三条棱长的比为1∶2∶3,对角线的长为2,求这个长方体的体积;
(2)如图,在三棱台ABC-A1B1C1中,AB∶A1B1=1∶2,求三棱锥A1-ABC,三棱锥B-A1B1C,三棱锥C-A1B1C1的体积之比.
2.(1)过长方体的一个顶点的三条棱长的比为1∶2∶3,对角线的长为2,求这个长方体的体积;
(2)如图,在三棱台ABC-A1B1C1中,AB∶A1B1=1∶2,求三棱锥A1-ABC,三棱锥B-A1B1C,三棱锥C-A1B1C1的体积之比.
3. (1)已知圆柱的侧面展开图是长、宽分别为2π和4π的矩形,求这个圆柱的体积;
(2)如图,圆台高为3,轴截面中母线AA1与底面直径AB的夹角为60°,轴截面中一条对角线垂直于腰,求圆台的体积.
(2)作轴截面A1ABB1,设上、下底面半径,母线长分别为r,R,l,作A1D⊥AB于点D.
不能把希望叫做白日做梦,也不能把白日之梦叫做希望。
引入:
祖暅,字景烁,祖冲之之子,范阳郡蓟县人(今河北省涞源县人),南北朝时代的伟大科学家。祖暅在数学上有突出贡献,他在实践的基础上,于5世纪末提出了体积的计算原理。祖暅原理:“幂势既同,则积不容异”。
“势”即是高,“幂”即是面积。
祖暅原理
祖暅原理的提出要比其他国家的数学家早一千多年。在欧洲直到17世纪,才有意大利数学家卡瓦列里提出上述结论。
祖冲之父子是
我们中华民族的
骄傲和自豪
1.了解祖暅原理.2.能运用公式求棱柱、棱锥、棱台、球体积.3.熟悉棱柱、棱锥、棱台之间的转换关系,培养转化与化归的思想与空间想象能力.
1.数学抽象:棱柱、棱锥、棱台的体积公式;2.数学运算:求多面体体积;3.数学建模:运用棱柱、棱锥、棱台的表面积和体积公式进行计算和解决有关实际问题.
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
知识点1:祖暅原理
答案:被平行于这两个平面的任意平面所截时,三棱锥和三棱柱不满足两个截面的面积总相等,故这两个几何体的体积不相等.
答案:根据祖暅原理,知三棱柱ABC-A1B1C1与圆柱O′O的体积相等.
问题2:柱体的体积
探究:如图,下面是底面积都等于S,高都等于h的任意棱柱,圆柱和长方体,你能用祖暅原理推导柱体的体积公式吗?
(1)结论:等底面积、等高的两个柱体,体积相等.
(2)体积:如果柱体的底面积为S,高为h,则柱体的体积计算公式为V柱体=Sh.
问题3:锥体的体积
探究:棱锥和圆锥的体积如何计算?
(1)结论:等底面积、等高的两个锥体,体积相等.
(2)体积:如果锥体的底面积为S,高为h,则锥体的体积计算公式为
V锥体= Sh.
【即时训练】
1.圆锥的底面半径为4,母线长为6,则体积为________.
问题4:台体的体积
探究:棱台、圆台的体积如何求解?
因为台体可以看成锥体截去一个小锥体得到,所以台体的体积可以通过计算锥体的体积之差来得到.
【即时训练】
已知棱台的上、下底面面积分别为4,16,高为3,则棱台的体积为________.
28
思考:柱体、锥体、球体的体积有什么关系?
问题5:球的体积
尝试与发现:
(1)你能想办法测出一个乒乓球的体积吗?
(2)如图所示是底面积和高都相等的两个几何体,左边是半球,右边是圆柱被挖去一个倒立的圆锥剩余的部分,用平行于半球与圆柱底面的平面去截这两个几何体,分别指出截面的形状,并讨论两个截面面积的大小关系,由此你能得到球的体积公式吗?
【即时训练】
1.若将球的半径扩大到原来的2倍,则它的体积增大到原来的( )
A.2倍 B.4倍
C.8倍 D.16倍
C
求多面体表面积的方法 1.多面体的表面积转化为各面面积之和.2.解决有关棱台的问题时,常用两种解题思路:一是把基本量转化到梯形中去解决;二是把棱台还原成棱锥,利用棱锥的有关知识来解决.
求几何体体积的方法①公式法:直接代入公式求解.②等积法:只需选用底面积和高都易求的形式即可.③分割法:将几何体分割成易求解的几部分,分别求体积
核心知识
方法总结
易错提醒
核心素养
棱柱、棱锥、棱台的体积
1.数学抽象:棱柱、棱锥、棱台的体积公式;
2.数学运算:求多面体或多面体组合体的表面积和体积;
3.数学建模:运用棱柱、棱锥、棱台的体积公式进行计算和解决有关实际问题.
棱锥
棱台
棱柱
棱柱、棱锥、棱台的体积
祖暅原理
祖暅原理:利用祖暅原理求不规则几何体的体积。
求几何体体积的方法①公式法:直接代入公式求解.②等积法:只需选用底面积和高都易求的形式即可.③分割法:将几何体分割成易求解的几部分分别求体积
柱、锥、台的体积的计算,一般要找出相应的底面和高,要充分利用截面、轴截面,求出所需要的量,最后代入公式计算.
1.正方体的表面积为96,则正方体的体积为( )
A.48 B.64 C.16 D.96
B
2.(1)过长方体的一个顶点的三条棱长的比为1∶2∶3,对角线的长为2,求这个长方体的体积;
(2)如图,在三棱台ABC-A1B1C1中,AB∶A1B1=1∶2,求三棱锥A1-ABC,三棱锥B-A1B1C,三棱锥C-A1B1C1的体积之比.
2.(1)过长方体的一个顶点的三条棱长的比为1∶2∶3,对角线的长为2,求这个长方体的体积;
(2)如图,在三棱台ABC-A1B1C1中,AB∶A1B1=1∶2,求三棱锥A1-ABC,三棱锥B-A1B1C,三棱锥C-A1B1C1的体积之比.
3. (1)已知圆柱的侧面展开图是长、宽分别为2π和4π的矩形,求这个圆柱的体积;
(2)如图,圆台高为3,轴截面中母线AA1与底面直径AB的夹角为60°,轴截面中一条对角线垂直于腰,求圆台的体积.
(2)作轴截面A1ABB1,设上、下底面半径,母线长分别为r,R,l,作A1D⊥AB于点D.
不能把希望叫做白日做梦,也不能把白日之梦叫做希望。
