11.3.3 平面与平面平行 课件(共27张PPT)
文档属性
| 名称 | 11.3.3 平面与平面平行 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 13:01:07 | ||
图片预览




文档简介
11.3.3平面与平面平行
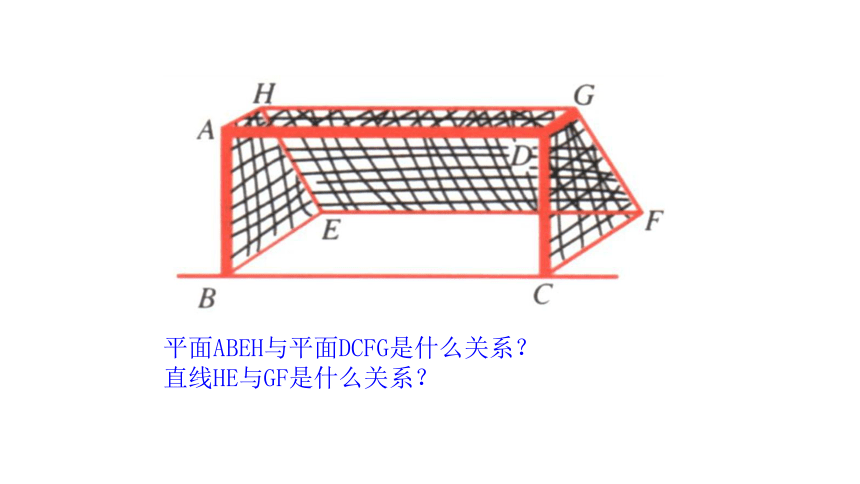
活动板房的前面板和后面板它们有什么关系呢?
平面ABEH与平面DCFG是什么关系?
直线HE与GF是什么关系?
1. 掌握两平面平行的判定和性质定理及其应用.
2.会用平面与平面平行的性质定理分析解决有关问题.
逻辑推理:在平行关系的转化证明过程中,培养逻辑推理的核心素养.
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
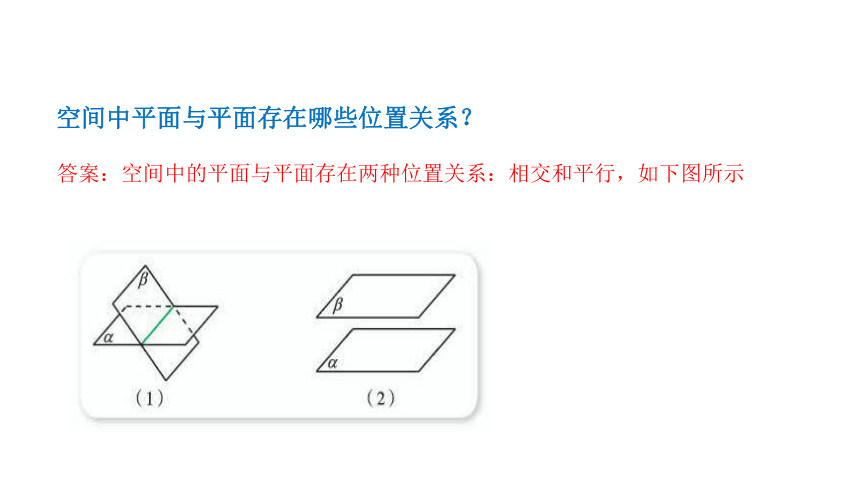
空间中平面与平面存在哪些位置关系?
答案:空间中的平面与平面存在两种位置关系:相交和平行,如下图所示
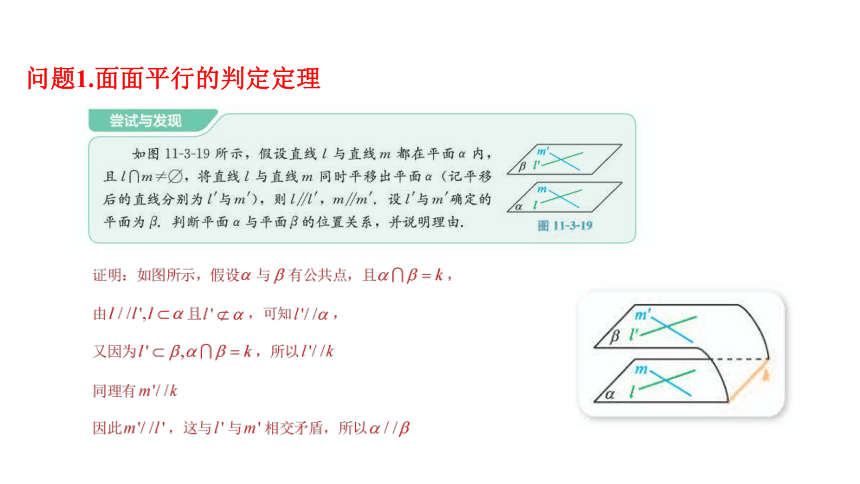
问题1.面面平行的判定定理
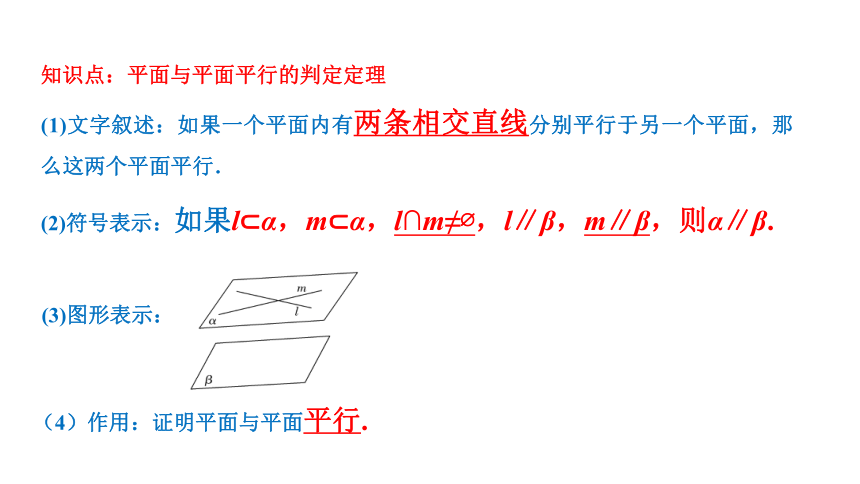
知识点:平面与平面平行的判定定理
(1)文字叙述:如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面平行.
(2)符号表示:如果l?α,m?α,l∩m≠?,l∥β,m∥β,则α∥β.
(3)图形表示:
(4)作用:证明平面与平面平行.
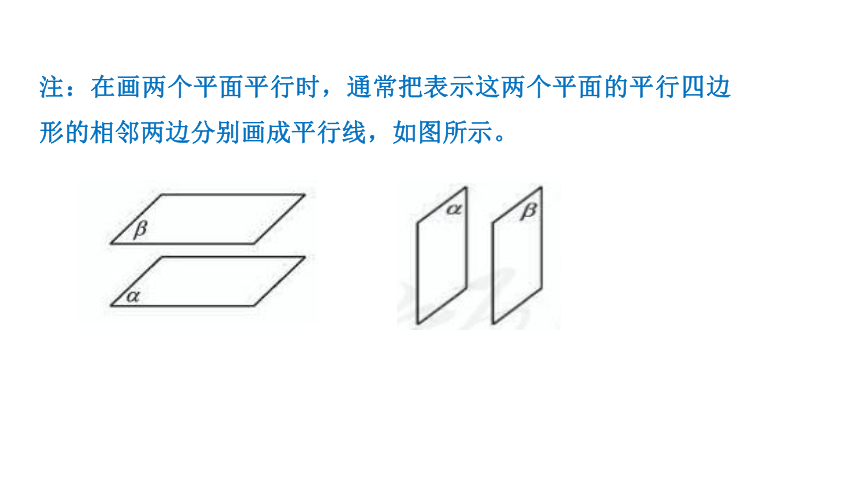
注:在画两个平面平行时,通常把表示这两个平面的平行四边形的相邻两边分别画成平行线,如图所示。
提示 平行.三角板的两条边相交,符合判定定理.
提示 不一定平行,若无数条直线都平行,那么这两个平面不一定平行;若无数条直线中存在两条相交直线,那么这两个平面就平行.
问题2:平面与平面平行判定定理的推论
(3)图形表示:
(4)作用:证明平面与平面平行.
在正方体ABCD-A1B1C1D1中,M、N、P分别是C1C、B1C1、C1D1的中点,求证:平面MNP∥平面A1BD.
【即时训练】
问题3:平面与平面平行的性质定理
知识点1 平面与平面平行的性质定理1
1.文字叙述:如果两个平面平行,那么其中一个平面内的直线平行于另一个平面
2.符号表示:如果α∥β,l?α,那么l∥β
3.图形表示:
4.作用:证明线面平行.
如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,P,Q分别是BC,C1D1,AD1,BD的中点.
求证:(1)PQ∥平面DCC1D1;
(2)EF∥平面BB1D1D.
【即时训练】
如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,P,Q分别是BC,C1D1,AD1,BD的中点.
求证:(1)PQ∥平面DCC1D1;
(2)EF∥平面BB1D1D.
【变式训练】
知识点2 平面与平面平行的性质定理2
1.文字叙述:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
2.符号表示:如果α∥β,α∩γ=l,β∩γ=m,则l∥m.
3.图形表示:
4.作用:证明两直线平行.
注:结论:两条直线被三个平行平面所截,截得的对应线段成比例.
平行关系的相互转化:
方法总结
核心知识
易错提醒
核心素养
1.平面与平面平行的判定
2.平面与平面平行的性质
应用性质定理时定理中的三个条件缺一不可
逻辑推理:在平行关系的转化证明过程中,培养逻辑推理的核心素养
线线平行
线面平行
面面平行
性质
判定定理
性质定理
判定定理
性质定理
平面与平面平行
性质
1.平面和平面平行的条件可以是( )
A.α内有无穷多条直线都与已知平面平行
B.直线a∥α,a∥β,且直线a不在α内,也不在β内
C.直线 ,直线 ,且a∥β,b∥α
D.α内的任何一条直线都与β平行
D
2.下列命题正确的是( )
A.夹在两个平行平面间的线段长度相等
B.平行于同一平面的两条直线平行
C.一条直线上有两点到一个平面的距离相
等,则这条直线与这个平面平行
D.过平面外一点有无数条直线与已知平面平行
D
3.平面α与圆台的上、下底面分别相交于直线m,n,
则m,n的位置关系是( )
A.相交 B.异面 C.平行 D.平行或异面
C
P
A
B
C
D
E
F
5.在三棱锥P-ABC中,点D、E、F分别是△PAB、△PBC、△PAC的重心,
求证:平面DEF//平面ABC.
M
N
O
证明:连接PD并延长交AB于点M
连接PE并延长交BC于点N,连接PF并延
长交AC于O,连接MN,MO,
因为D,E分别为△PAB、
△PBC的重心所以 DE∥MN,又
因为DE 面ABC,MN 面ABC
所以DE∥面ABC,同理:DF∥面ABC
又因为DE∩DF=D 所以面DEF∥面ABC
不轻易献出成功的皇冠乃是困难的天性。
活动板房的前面板和后面板它们有什么关系呢?
平面ABEH与平面DCFG是什么关系?
直线HE与GF是什么关系?
1. 掌握两平面平行的判定和性质定理及其应用.
2.会用平面与平面平行的性质定理分析解决有关问题.
逻辑推理:在平行关系的转化证明过程中,培养逻辑推理的核心素养.
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
空间中平面与平面存在哪些位置关系?
答案:空间中的平面与平面存在两种位置关系:相交和平行,如下图所示
问题1.面面平行的判定定理
知识点:平面与平面平行的判定定理
(1)文字叙述:如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面平行.
(2)符号表示:如果l?α,m?α,l∩m≠?,l∥β,m∥β,则α∥β.
(3)图形表示:
(4)作用:证明平面与平面平行.
注:在画两个平面平行时,通常把表示这两个平面的平行四边形的相邻两边分别画成平行线,如图所示。
提示 平行.三角板的两条边相交,符合判定定理.
提示 不一定平行,若无数条直线都平行,那么这两个平面不一定平行;若无数条直线中存在两条相交直线,那么这两个平面就平行.
问题2:平面与平面平行判定定理的推论
(3)图形表示:
(4)作用:证明平面与平面平行.
在正方体ABCD-A1B1C1D1中,M、N、P分别是C1C、B1C1、C1D1的中点,求证:平面MNP∥平面A1BD.
【即时训练】
问题3:平面与平面平行的性质定理
知识点1 平面与平面平行的性质定理1
1.文字叙述:如果两个平面平行,那么其中一个平面内的直线平行于另一个平面
2.符号表示:如果α∥β,l?α,那么l∥β
3.图形表示:
4.作用:证明线面平行.
如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,P,Q分别是BC,C1D1,AD1,BD的中点.
求证:(1)PQ∥平面DCC1D1;
(2)EF∥平面BB1D1D.
【即时训练】
如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,P,Q分别是BC,C1D1,AD1,BD的中点.
求证:(1)PQ∥平面DCC1D1;
(2)EF∥平面BB1D1D.
【变式训练】
知识点2 平面与平面平行的性质定理2
1.文字叙述:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
2.符号表示:如果α∥β,α∩γ=l,β∩γ=m,则l∥m.
3.图形表示:
4.作用:证明两直线平行.
注:结论:两条直线被三个平行平面所截,截得的对应线段成比例.
平行关系的相互转化:
方法总结
核心知识
易错提醒
核心素养
1.平面与平面平行的判定
2.平面与平面平行的性质
应用性质定理时定理中的三个条件缺一不可
逻辑推理:在平行关系的转化证明过程中,培养逻辑推理的核心素养
线线平行
线面平行
面面平行
性质
判定定理
性质定理
判定定理
性质定理
平面与平面平行
性质
1.平面和平面平行的条件可以是( )
A.α内有无穷多条直线都与已知平面平行
B.直线a∥α,a∥β,且直线a不在α内,也不在β内
C.直线 ,直线 ,且a∥β,b∥α
D.α内的任何一条直线都与β平行
D
2.下列命题正确的是( )
A.夹在两个平行平面间的线段长度相等
B.平行于同一平面的两条直线平行
C.一条直线上有两点到一个平面的距离相
等,则这条直线与这个平面平行
D.过平面外一点有无数条直线与已知平面平行
D
3.平面α与圆台的上、下底面分别相交于直线m,n,
则m,n的位置关系是( )
A.相交 B.异面 C.平行 D.平行或异面
C
P
A
B
C
D
E
F
5.在三棱锥P-ABC中,点D、E、F分别是△PAB、△PBC、△PAC的重心,
求证:平面DEF//平面ABC.
M
N
O
证明:连接PD并延长交AB于点M
连接PE并延长交BC于点N,连接PF并延
长交AC于O,连接MN,MO,
因为D,E分别为△PAB、
△PBC的重心所以 DE∥MN,又
因为DE 面ABC,MN 面ABC
所以DE∥面ABC,同理:DF∥面ABC
又因为DE∩DF=D 所以面DEF∥面ABC
不轻易献出成功的皇冠乃是困难的天性。
