11.4.2 平面与平面垂直 课件(共33张PPT)
文档属性
| 名称 | 11.4.2 平面与平面垂直 课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 00:00:00 | ||
图片预览





文档简介
11.4.2平面与平面垂直
1.使学生正确理解和掌握 “二面角”、“二面角的平面角”及“直二面角”、“两个平面互相垂直”的概念.2.掌握两个平面垂直的判定定理并能进行简单应用.
1.逻辑推理:面面垂直的证明问题涉及逻辑推理及其转化思想
2.直观想象:求解二面角的问题
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
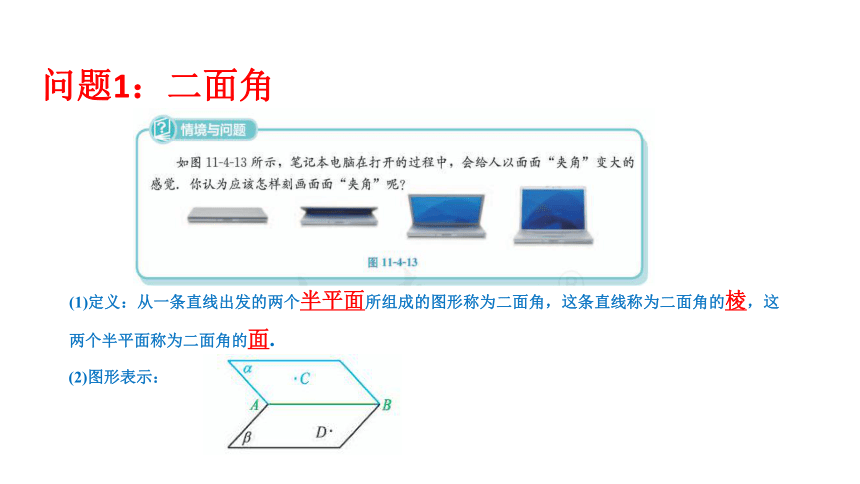
问题1:二面角
(1)定义:从一条直线出发的两个半平面所组成的图形称为二面角,这条直线称为二面角的棱,这两个半平面称为二面角的面.
(2)图形表示:
(1)定义:从一条直线出发的两个半平面所组成的图形称为二面角,这条直线称为二面角的棱,这两个半平面称为二面角的面.
(2)图形表示:
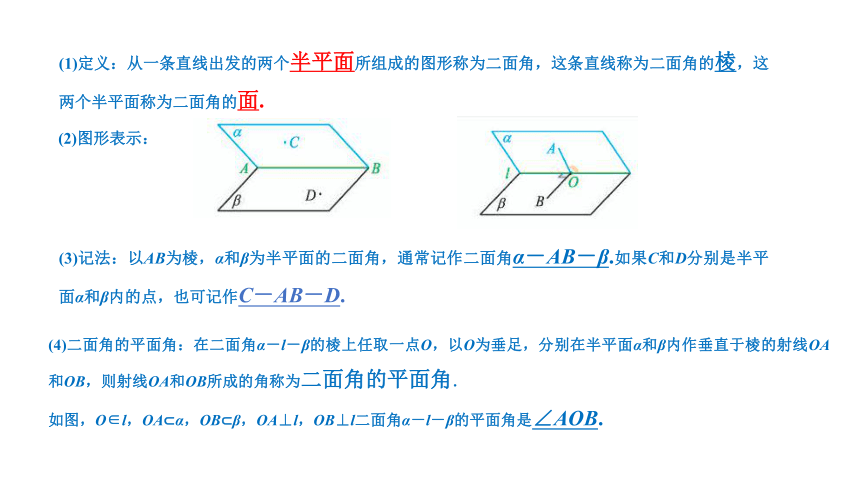
(3)记法:以AB为棱,α和β为半平面的二面角,通常记作二面角α-AB-β.如果C和D分别是半平面α和β内的点,也可记作C-AB-D.
(4)二面角的平面角:在二面角α-l-β的棱上任取一点O,以O为垂足,分别在半平面α和β内作垂直于棱的射线OA和OB,则射线OA和OB所成的角称为二面角的平面角.
如图,O∈l,OA?α,OB?β,OA⊥l,OB⊥l二面角α-l-β的平面角是∠AOB.
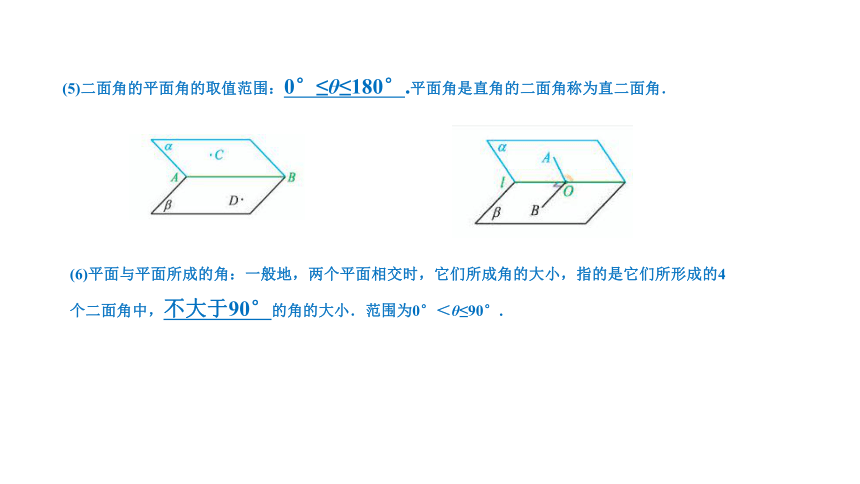
(5)二面角的平面角的取值范围:0°≤θ≤180°.平面角是直角的二面角称为直二面角.
(6)平面与平面所成的角:一般地,两个平面相交时,它们所成角的大小,指的是它们所形成的4个二面角中,不大于90°的角的大小.范围为0°<θ≤90°.
【即时训练】
判断正误.
(1)两个相交平面组成的图形叫做二面角. ( )
(2)异面直线a,b分别和一个二面角的两个半平面垂直,则a,b所成的角与这个二面角的平面角相等或互补. ( )
(3)二面角的平面角是从棱上一点出发,分别在两个半平面内作射线所成角的最小角. ( )
(4)二面角的大小与其平面角的顶点在棱上的位置没有关系. ( )
答案:(1)× (2)√ (3)× (4)√
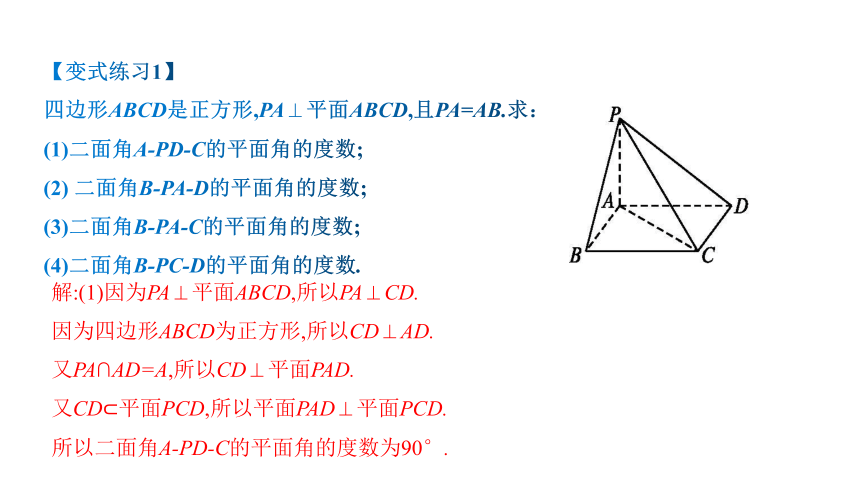
解:(1)因为PA⊥平面ABCD,所以PA⊥CD.
因为四边形ABCD为正方形,所以CD⊥AD.
又PA∩AD=A,所以CD⊥平面PAD.
又CD?平面PCD,所以平面PAD⊥平面PCD.
所以二面角A-PD-C的平面角的度数为90°.
【变式练习1】
四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.求:
(1)二面角A-PD-C的平面角的度数;
(2) 二面角B-PA-D的平面角的度数;
(3)二面角B-PA-C的平面角的度数;
(4)二面角B-PC-D的平面角的度数.
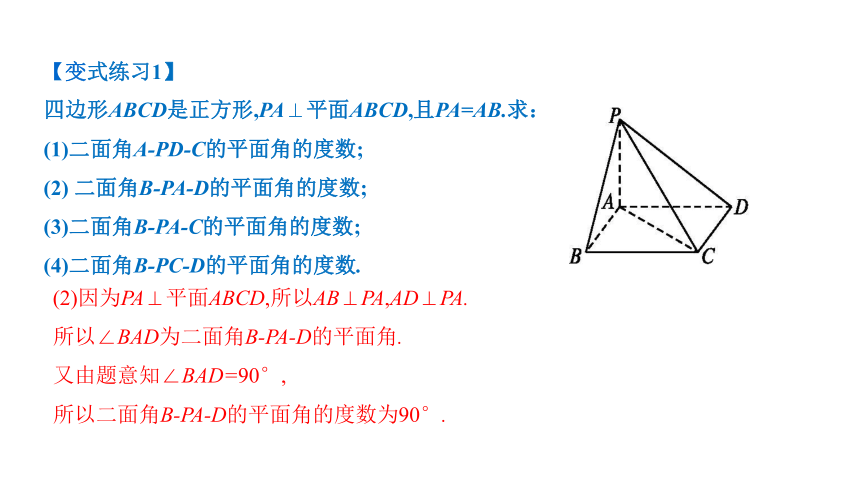
(2)因为PA⊥平面ABCD,所以AB⊥PA,AD⊥PA.
所以∠BAD为二面角B-PA-D的平面角.
又由题意知∠BAD=90°,
所以二面角B-PA-D的平面角的度数为90°.
【变式练习1】
四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.求:
(1)二面角A-PD-C的平面角的度数;
(2) 二面角B-PA-D的平面角的度数;
(3)二面角B-PA-C的平面角的度数;
(4)二面角B-PC-D的平面角的度数.
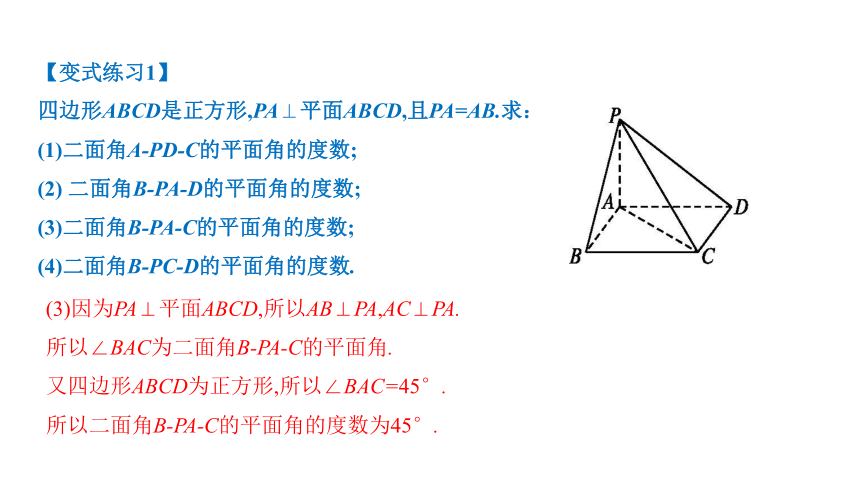
(3)因为PA⊥平面ABCD,所以AB⊥PA,AC⊥PA.
所以∠BAC为二面角B-PA-C的平面角.
又四边形ABCD为正方形,所以∠BAC=45°.
所以二面角B-PA-C的平面角的度数为45°.
【变式练习1】
四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.求:
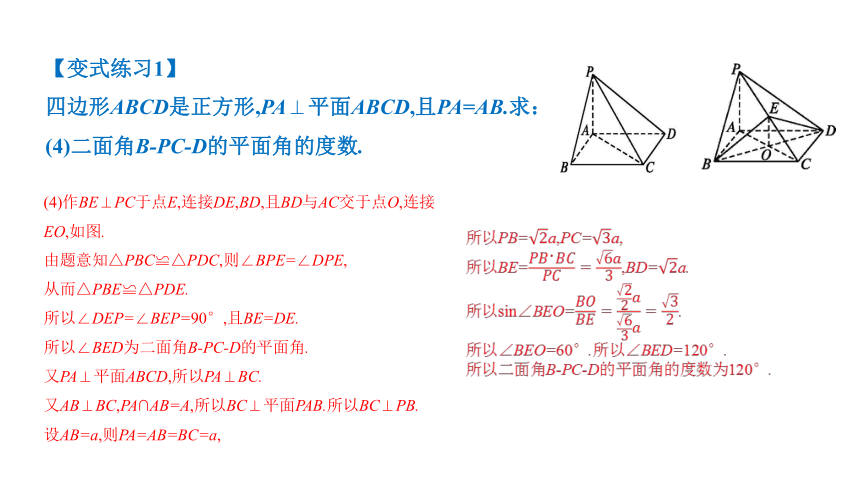
(4)二面角B-PC-D的平面角的度数.
(4)作BE⊥PC于点E,连接DE,BD,且BD与AC交于点O,连接EO,如图.
由题意知△PBC≌△PDC,则∠BPE=∠DPE,
从而△PBE≌△PDE.
所以∠DEP=∠BEP=90°,且BE=DE.
所以∠BED为二面角B-PC-D的平面角.
又PA⊥平面ABCD,所以PA⊥BC.
又AB⊥BC,PA∩AB=A,所以BC⊥平面PAB.所以BC⊥PB.
设AB=a,则PA=AB=BC=a,
【解题方法】
方法一(定义法):在二面角的棱上找一个特殊点,在两个半平面内分别作垂直于棱的射线.
如图所示,∠AOB为二面角α-a-β的平面角.
方法二(垂线法):过二面角的一个面内的一点作另一个平面的垂线,过垂足作棱的垂线,利用线面垂直可找到二面角的平面角或其补角.
如图所示,∠AFE为二面角A-BC-D的平面角.
方法三(垂面法):过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角,即二面角的平面角.
如图所示,∠AOB为二面角α-l-β的平面角.
问题2:平面与平面垂直
1.定义:一般地,如果两个平面α与β所成角的大小为90°,则称这两个平面互相垂直,记作α⊥β.
2.画法
3.判定定理
(1)文字叙述:如果一个平面经过另外一个平面的一条垂线,则这两个平面互相垂直.
(2)图形表示:
(3)符号表示:如果l?α,l⊥β,则α⊥β.
(4)作用:证明平面与平面垂直.
注:由面面垂直的判定定理,容易证明直棱柱的每个侧面都与底面互相垂直,理由是直棱柱的侧棱垂直于底面。
【即时训练】
1.经过平面α外一点和平面α内一点与平面α垂直的平面有 _ _______个.
答案:1个或无数个
设平面外一点为A,平面内一点为B,过点A作平面α的垂线l,若点B恰为垂足,则所有过AB的平面均与α垂直,此时有无数个平面与α垂直;若点B不是垂足,则l与点B确定唯一平面β满足α⊥β.
2.在三棱锥P-ABC中,已知PA⊥PB,PB⊥PC,PC⊥PA,如图,则在三棱锥P-ABC的四个面中,互相垂直的面有________对.
答案:3 平面PAB⊥平面PAC,平面PAB⊥平面PBC,平面PAC⊥平面PBC.
1个或无数
3
问题2:平面与平面垂直的判定和性质定理综合应用
【变式练习1】
如图,AB是☉O的直径,C是圆周上不同于A,B的任意一点,平面PAC⊥平面ABC.
(1)判断BC与平面PAC的位置关系,并证明.
(2)判断平面PBC与平面PAC的位置关系.
解:(1)BC⊥平面PAC.
证明:因为AB是☉O的直径,C是圆周上不同于A,B的任意一点,所以∠ACB=90°,所以BC⊥AC.
又因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,BC?平面ABC,所以BC⊥平面PAC.
(2)因为BC?平面PBC,所以平面PBC⊥平面PAC.
2.如图,在正三棱柱ABC-A1B1C1中,D为BC的中点,点E在AC上,且DE⊥A1E.
(1)求证:平面A1AD⊥平面BCC1B1;
(2)求证:平面A1DE⊥平面ACC1A1.
证明 (1)因为ABC-A1B1C1为正三棱柱,
所以BB1⊥平面ABC,又AD?平面ABC,
所以AD⊥BB1,又D为BC的中点,
所以AD⊥BC,又BC∩BB1=B,BC,BB1?平面BCC1B1.
所以AD⊥平面BCC1B1.又AD?平面ADA1,
所以平面A1AD⊥平面BCC1B1.
(2)因为ABC-A1B1C1为正三棱柱,
所以AA1⊥平面ABC,又DE?平面ABC,
所以AA1⊥DE,因为DE⊥A1E,
又A1E∩AA1=A1,
所以DE⊥平面ACC1A1,
又DE?平面A1DE,所以平面A1DE⊥平面ACC1A1.
【变式练习2】
【解题方法】
面面垂直的方法
(1)定义法:即说明两个半平面所成的二面角是直二面角;
(2)判定定理法:在其中一个平面内寻找一条直线与另一个平面垂直,即把问题转化为“线面垂直”;
(3)性质法:两个平行平面中的一个垂直于第三个平面,则另一个也垂直于此平面.
【变式练习】 若本例改为:在正三棱柱ABC-A1B1C1中,F为A1C1的中点,求证:平面AB1F⊥平面ACC1A1.
【变式练习3】
如图所示,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.求证:平面ABC⊥平面SBC.
证明:方法一:(利用定义证明)
因为∠BSA=∠CSA=60°,SA=SB=SC,
所以△ASB和△ASC是等边三角形,
令SA=SB=SC=AB=AC=a,
则△ABC和△SBC为共底边BC的等腰三角形.
取BC的中点D,如图所示,连接AD,SD,
方法二:(利用判定定理)
因为SA=SB=SC,且∠BSA=∠CSA=60°,
所以SA=AB=AC,
所以点A在平面SBC上的射影为△SBC的外心.
所以△SBC为直角三角形,
所以点A在△SBC上的射影D为斜边BC的中点,
所以AD⊥平面SBC.
又所以AD?平面ABC,所以平面ABC⊥平面SBC.
【变式练习4】
如图所示,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.求证:平面ABC⊥平面SBC.
易错提醒
核心知识
方法总结
核心素养
直观想象:求解二面角的问题
求二面角时注意是锐角还是钝角
平面与
平面垂直
(一)
面面垂直的判断方法:
(1)利用定义:作二面角的平面角→证明为直角
(2)判定定理:转化为证线面垂直,即在一个面内找一条直线与另一个平面垂直
二面角的求法:作出二面角的平面角并证明,将作出的角放在三角形中求解
逻辑推理:面面垂直的证明问题涉及逻辑推理及其转化思想
在证明面面垂直时注意满足的条件
二面角
定义
判定定理
应用
D
D
不如意的时候不要尽往悲伤里钻,想想有笑声的日子吧!
1.使学生正确理解和掌握 “二面角”、“二面角的平面角”及“直二面角”、“两个平面互相垂直”的概念.2.掌握两个平面垂直的判定定理并能进行简单应用.
1.逻辑推理:面面垂直的证明问题涉及逻辑推理及其转化思想
2.直观想象:求解二面角的问题
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
问题1:二面角
(1)定义:从一条直线出发的两个半平面所组成的图形称为二面角,这条直线称为二面角的棱,这两个半平面称为二面角的面.
(2)图形表示:
(1)定义:从一条直线出发的两个半平面所组成的图形称为二面角,这条直线称为二面角的棱,这两个半平面称为二面角的面.
(2)图形表示:
(3)记法:以AB为棱,α和β为半平面的二面角,通常记作二面角α-AB-β.如果C和D分别是半平面α和β内的点,也可记作C-AB-D.
(4)二面角的平面角:在二面角α-l-β的棱上任取一点O,以O为垂足,分别在半平面α和β内作垂直于棱的射线OA和OB,则射线OA和OB所成的角称为二面角的平面角.
如图,O∈l,OA?α,OB?β,OA⊥l,OB⊥l二面角α-l-β的平面角是∠AOB.
(5)二面角的平面角的取值范围:0°≤θ≤180°.平面角是直角的二面角称为直二面角.
(6)平面与平面所成的角:一般地,两个平面相交时,它们所成角的大小,指的是它们所形成的4个二面角中,不大于90°的角的大小.范围为0°<θ≤90°.
【即时训练】
判断正误.
(1)两个相交平面组成的图形叫做二面角. ( )
(2)异面直线a,b分别和一个二面角的两个半平面垂直,则a,b所成的角与这个二面角的平面角相等或互补. ( )
(3)二面角的平面角是从棱上一点出发,分别在两个半平面内作射线所成角的最小角. ( )
(4)二面角的大小与其平面角的顶点在棱上的位置没有关系. ( )
答案:(1)× (2)√ (3)× (4)√
解:(1)因为PA⊥平面ABCD,所以PA⊥CD.
因为四边形ABCD为正方形,所以CD⊥AD.
又PA∩AD=A,所以CD⊥平面PAD.
又CD?平面PCD,所以平面PAD⊥平面PCD.
所以二面角A-PD-C的平面角的度数为90°.
【变式练习1】
四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.求:
(1)二面角A-PD-C的平面角的度数;
(2) 二面角B-PA-D的平面角的度数;
(3)二面角B-PA-C的平面角的度数;
(4)二面角B-PC-D的平面角的度数.
(2)因为PA⊥平面ABCD,所以AB⊥PA,AD⊥PA.
所以∠BAD为二面角B-PA-D的平面角.
又由题意知∠BAD=90°,
所以二面角B-PA-D的平面角的度数为90°.
【变式练习1】
四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.求:
(1)二面角A-PD-C的平面角的度数;
(2) 二面角B-PA-D的平面角的度数;
(3)二面角B-PA-C的平面角的度数;
(4)二面角B-PC-D的平面角的度数.
(3)因为PA⊥平面ABCD,所以AB⊥PA,AC⊥PA.
所以∠BAC为二面角B-PA-C的平面角.
又四边形ABCD为正方形,所以∠BAC=45°.
所以二面角B-PA-C的平面角的度数为45°.
【变式练习1】
四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.求:
(4)二面角B-PC-D的平面角的度数.
(4)作BE⊥PC于点E,连接DE,BD,且BD与AC交于点O,连接EO,如图.
由题意知△PBC≌△PDC,则∠BPE=∠DPE,
从而△PBE≌△PDE.
所以∠DEP=∠BEP=90°,且BE=DE.
所以∠BED为二面角B-PC-D的平面角.
又PA⊥平面ABCD,所以PA⊥BC.
又AB⊥BC,PA∩AB=A,所以BC⊥平面PAB.所以BC⊥PB.
设AB=a,则PA=AB=BC=a,
【解题方法】
方法一(定义法):在二面角的棱上找一个特殊点,在两个半平面内分别作垂直于棱的射线.
如图所示,∠AOB为二面角α-a-β的平面角.
方法二(垂线法):过二面角的一个面内的一点作另一个平面的垂线,过垂足作棱的垂线,利用线面垂直可找到二面角的平面角或其补角.
如图所示,∠AFE为二面角A-BC-D的平面角.
方法三(垂面法):过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角,即二面角的平面角.
如图所示,∠AOB为二面角α-l-β的平面角.
问题2:平面与平面垂直
1.定义:一般地,如果两个平面α与β所成角的大小为90°,则称这两个平面互相垂直,记作α⊥β.
2.画法
3.判定定理
(1)文字叙述:如果一个平面经过另外一个平面的一条垂线,则这两个平面互相垂直.
(2)图形表示:
(3)符号表示:如果l?α,l⊥β,则α⊥β.
(4)作用:证明平面与平面垂直.
注:由面面垂直的判定定理,容易证明直棱柱的每个侧面都与底面互相垂直,理由是直棱柱的侧棱垂直于底面。
【即时训练】
1.经过平面α外一点和平面α内一点与平面α垂直的平面有 _ _______个.
答案:1个或无数个
设平面外一点为A,平面内一点为B,过点A作平面α的垂线l,若点B恰为垂足,则所有过AB的平面均与α垂直,此时有无数个平面与α垂直;若点B不是垂足,则l与点B确定唯一平面β满足α⊥β.
2.在三棱锥P-ABC中,已知PA⊥PB,PB⊥PC,PC⊥PA,如图,则在三棱锥P-ABC的四个面中,互相垂直的面有________对.
答案:3 平面PAB⊥平面PAC,平面PAB⊥平面PBC,平面PAC⊥平面PBC.
1个或无数
3
问题2:平面与平面垂直的判定和性质定理综合应用
【变式练习1】
如图,AB是☉O的直径,C是圆周上不同于A,B的任意一点,平面PAC⊥平面ABC.
(1)判断BC与平面PAC的位置关系,并证明.
(2)判断平面PBC与平面PAC的位置关系.
解:(1)BC⊥平面PAC.
证明:因为AB是☉O的直径,C是圆周上不同于A,B的任意一点,所以∠ACB=90°,所以BC⊥AC.
又因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,BC?平面ABC,所以BC⊥平面PAC.
(2)因为BC?平面PBC,所以平面PBC⊥平面PAC.
2.如图,在正三棱柱ABC-A1B1C1中,D为BC的中点,点E在AC上,且DE⊥A1E.
(1)求证:平面A1AD⊥平面BCC1B1;
(2)求证:平面A1DE⊥平面ACC1A1.
证明 (1)因为ABC-A1B1C1为正三棱柱,
所以BB1⊥平面ABC,又AD?平面ABC,
所以AD⊥BB1,又D为BC的中点,
所以AD⊥BC,又BC∩BB1=B,BC,BB1?平面BCC1B1.
所以AD⊥平面BCC1B1.又AD?平面ADA1,
所以平面A1AD⊥平面BCC1B1.
(2)因为ABC-A1B1C1为正三棱柱,
所以AA1⊥平面ABC,又DE?平面ABC,
所以AA1⊥DE,因为DE⊥A1E,
又A1E∩AA1=A1,
所以DE⊥平面ACC1A1,
又DE?平面A1DE,所以平面A1DE⊥平面ACC1A1.
【变式练习2】
【解题方法】
面面垂直的方法
(1)定义法:即说明两个半平面所成的二面角是直二面角;
(2)判定定理法:在其中一个平面内寻找一条直线与另一个平面垂直,即把问题转化为“线面垂直”;
(3)性质法:两个平行平面中的一个垂直于第三个平面,则另一个也垂直于此平面.
【变式练习】 若本例改为:在正三棱柱ABC-A1B1C1中,F为A1C1的中点,求证:平面AB1F⊥平面ACC1A1.
【变式练习3】
如图所示,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.求证:平面ABC⊥平面SBC.
证明:方法一:(利用定义证明)
因为∠BSA=∠CSA=60°,SA=SB=SC,
所以△ASB和△ASC是等边三角形,
令SA=SB=SC=AB=AC=a,
则△ABC和△SBC为共底边BC的等腰三角形.
取BC的中点D,如图所示,连接AD,SD,
方法二:(利用判定定理)
因为SA=SB=SC,且∠BSA=∠CSA=60°,
所以SA=AB=AC,
所以点A在平面SBC上的射影为△SBC的外心.
所以△SBC为直角三角形,
所以点A在△SBC上的射影D为斜边BC的中点,
所以AD⊥平面SBC.
又所以AD?平面ABC,所以平面ABC⊥平面SBC.
【变式练习4】
如图所示,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC.求证:平面ABC⊥平面SBC.
易错提醒
核心知识
方法总结
核心素养
直观想象:求解二面角的问题
求二面角时注意是锐角还是钝角
平面与
平面垂直
(一)
面面垂直的判断方法:
(1)利用定义:作二面角的平面角→证明为直角
(2)判定定理:转化为证线面垂直,即在一个面内找一条直线与另一个平面垂直
二面角的求法:作出二面角的平面角并证明,将作出的角放在三角形中求解
逻辑推理:面面垂直的证明问题涉及逻辑推理及其转化思想
在证明面面垂直时注意满足的条件
二面角
定义
判定定理
应用
D
D
不如意的时候不要尽往悲伤里钻,想想有笑声的日子吧!
