11.2 平面的基本事实与推论 课件(共34张PPT)
文档属性
| 名称 | 11.2 平面的基本事实与推论 课件(共34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 13:15:00 | ||
图片预览









文档简介
(共34张PPT)
11.2平面的基本事实与推论
1.了解空间中确定平面的条件 2.会用数学语言表示点线面之间的关系、会用符号语言和图形语言表示.
数学抽象:三种语言之间的相互转化
直观想象:空间中确定平面的条件
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
在初中几何中,学习过哪些点与直线的基本事实?
(1)连接两点的线中,线段最短;
(2)过两点有一条直线,并且只有一条直线.
结论(2)也可以简单地说成“两点确定一条直线”.
事实上,通过指定的一个点可以作无数条直线,通过指定的三个点,不一定能作一条直线。
问题1:平面的基本事实
基本事实1:
图形表示:
注:(1)可以简单地说成“不共线的3点确定一个平面”
(2)过不共线的3点A,B,C的平面,通常记作平面ABC,用图形直观地表示平面时,为了增加立体感,习惯上将平面用平行四边形表示.
(4)如果给定的3个点在同一直线上,那么有无数个平面通过这3个点,也就是说,此时这三个点不能“确定”一个平面.例如,如果给定的3个点都在长方体的一条棱上,那么过这三个点就会有无数个平面.
作用:
①确定平面的依据;
②判定点、线共面
基本事实2:
图形表示:
作用:
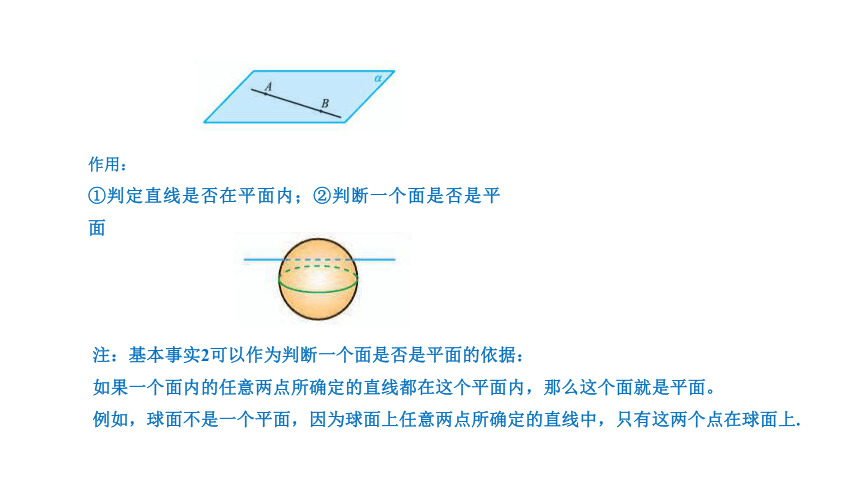
①判定直线是否在平面内;②判断一个面是否是平面
注:基本事实2可以作为判断一个面是否是平面的依据:
如果一个面内的任意两点所确定的直线都在这个平面内,那么这个面就是平面。
例如,球面不是一个平面,因为球面上任意两点所确定的直线中,只有这两个点在球面上.
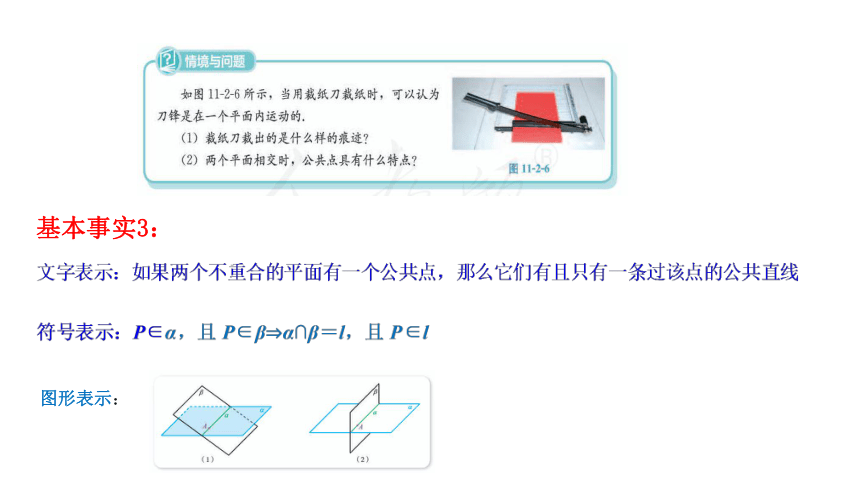
基本事实3:
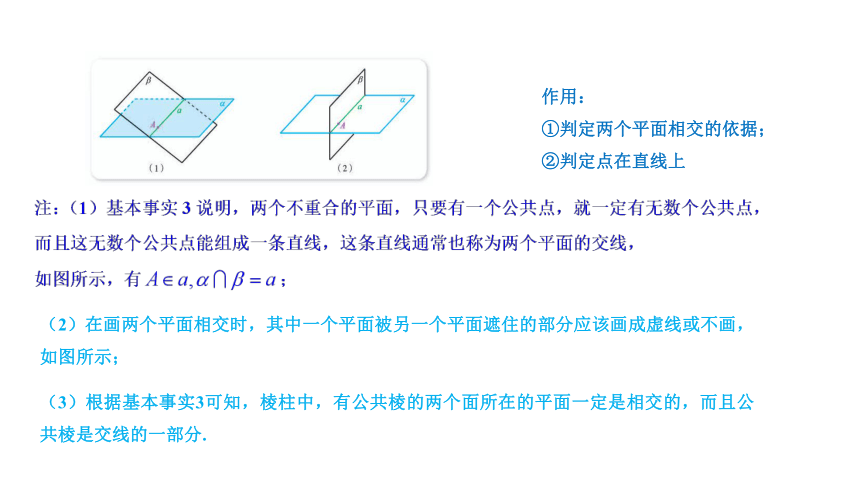
图形表示:
(2)在画两个平面相交时,其中一个平面被另一个平面遮住的部分应该画成虚线或不画,如图所示;
(3)根据基本事实3可知,棱柱中,有公共棱的两个面所在的平面一定是相交的,而且公共棱是交线的一部分.
作用:
①判定两个平面相交的依据;
②判定点在直线上
【即时训练】
1.下列说法正确的是( )
A.三点可以确定一个平面
B.若直线上有一个点在一个平面内,则这条直线在这个平面内
C.把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面相交于一点
D.如果两个平面有三个不共线的点,那么这两个平面重合
D
2.若A∈平面α,B∈平面α,C∈直线AB,则( )
A.C∈α B.C α
C.AB α D.AB∩α=C
答案:A
因为A∈平面α,B∈平面α,所以AB α.又因为C∈直线AB,所以C∈α.
A
问题2:由平面的基本事实得到的推论
推论1:
图形表示:
(2)推论1可以简单地说成:直线和直线外一点确定一个平面.
推论2:
文字表示:经过两条相交直线,有且只有一个平面.
符号表示:l∩m=A 存在唯一的平面α,使l α,且m α
图形表示:
推论3:
文字表示:经过两条平行直线,有且只有一个平面
符号表示:l∥m 存在唯一的平面α,使l α,且m α
图形表示:
注:(1)推论2与推论3可以分别简单地说成“两条相交直线确定一个平面”,“两条平行直线确定一个平面”。
(2)推论2可以说明,三角形是平面图形,因此初中有关三角形全等,相似,以及前面我们学习的解三角形等结论,在空间中也是成立的。
(3)推论3可以说明平行四边形,梯形也是平面图形,初中有关平行四边形、梯形的判定与性质等结论,在空间中也成立.
【即时训练】
1.下列说法不正确的是( )
A.三角形是平面图形 B.一条直线和一个点可以确定一个平面
C.平行四边形是平面图形 D.初中学习的梯形的判断与性质等结论,在空间中仍然成立
B
2.经过空间任意三点作平面( )
A.只有一个 B.可作二个
C.可作无数多个 D.只有一个或有无数多个
答案:D 当三点在一条直线上时,过这三点的平面能作无数个;当三点不在同一条直线上时,过这三点的平面有且只有一个.
D
例1.证明:两两相交且不过同一个点的3条直线必在同一个平面内.
证明 在△ABD中,
因为E,H分别是AB,AD的中点,
所以EH∥BD.
同理FG∥BD,则EH∥FG.
故E,F,G,H四点共面.
小结:
1.证明三点共线的方法:先考虑两个平面的交线,再证有关的点都是这两个平面的公共点.或先由某两点作一直线,再证明其他点也在这条直线上.
2.证明点线共面的方法:先由有关元素确定一个基本平面,再证其他的点(或线)在这个平面内;或先由部分点线确定平面,再由其他点线确定平面,然后证明这些平面重合.注意对诸如“两平行直线确定一个平面”等依据的证明、记忆与运用.
3.证明多线共点的方法:先证两线共点,再证这个点在其他直线上,而“其他”直线往往归结为平面与平面的交线.
平面的基本事实与推论
核心知识
方法总结
易错提醒
核心素养
1会用数学语言描述点、线、面之间的位置关系
2.会证明推论1、推论2、推论3.
数学抽象:三种语言之间的相互转化
经过不在一直线上的三点,有且只有一平面
确定平面的条件
直观想象:点、线、面之间数学语言表示
一条直线上的两个点在平面内,那么直线
就在平面内
两个不重合的平面有一个公共点,那么它
们有且只有过该点的公共直线
证明 因为MN∩EF=Q,
所以Q∈直线MN,Q∈直线EF.
又因为M∈CD,N∈直线AB,CD 平面ABCD,
AB 平面ABCD直线,
所以M,N∈平面ABCD,所以MN 平面ABCD.
所以Q∈平面ABCD.同理,可得EF 平面ADD1A1,
所以Q∈平面ADD1A1.
又因为平面ABCD∩平面ADD1A1=AD,
所以Q∈直线AD,即D,A,Q三点共线.
(2)符号语言表示:平面ABD∩平面BDC=BD,
平面ABC∩平面ADC=AC.
图形表示如图②.
答案:D A是基本事实2,故A正确;
B是基本事实3,故B正确;
C是基本事实1,故C正确;
当l α,A∈l时,也有可能A∈α,如l∩α=A,故D不正确.
D
不能因为第一次飞翔遇到了乌云风暴,从此就怀疑没有蓝天彩霞。
11.2平面的基本事实与推论
1.了解空间中确定平面的条件 2.会用数学语言表示点线面之间的关系、会用符号语言和图形语言表示.
数学抽象:三种语言之间的相互转化
直观想象:空间中确定平面的条件
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
在初中几何中,学习过哪些点与直线的基本事实?
(1)连接两点的线中,线段最短;
(2)过两点有一条直线,并且只有一条直线.
结论(2)也可以简单地说成“两点确定一条直线”.
事实上,通过指定的一个点可以作无数条直线,通过指定的三个点,不一定能作一条直线。
问题1:平面的基本事实
基本事实1:
图形表示:
注:(1)可以简单地说成“不共线的3点确定一个平面”
(2)过不共线的3点A,B,C的平面,通常记作平面ABC,用图形直观地表示平面时,为了增加立体感,习惯上将平面用平行四边形表示.
(4)如果给定的3个点在同一直线上,那么有无数个平面通过这3个点,也就是说,此时这三个点不能“确定”一个平面.例如,如果给定的3个点都在长方体的一条棱上,那么过这三个点就会有无数个平面.
作用:
①确定平面的依据;
②判定点、线共面
基本事实2:
图形表示:
作用:
①判定直线是否在平面内;②判断一个面是否是平面
注:基本事实2可以作为判断一个面是否是平面的依据:
如果一个面内的任意两点所确定的直线都在这个平面内,那么这个面就是平面。
例如,球面不是一个平面,因为球面上任意两点所确定的直线中,只有这两个点在球面上.
基本事实3:
图形表示:
(2)在画两个平面相交时,其中一个平面被另一个平面遮住的部分应该画成虚线或不画,如图所示;
(3)根据基本事实3可知,棱柱中,有公共棱的两个面所在的平面一定是相交的,而且公共棱是交线的一部分.
作用:
①判定两个平面相交的依据;
②判定点在直线上
【即时训练】
1.下列说法正确的是( )
A.三点可以确定一个平面
B.若直线上有一个点在一个平面内,则这条直线在这个平面内
C.把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面相交于一点
D.如果两个平面有三个不共线的点,那么这两个平面重合
D
2.若A∈平面α,B∈平面α,C∈直线AB,则( )
A.C∈α B.C α
C.AB α D.AB∩α=C
答案:A
因为A∈平面α,B∈平面α,所以AB α.又因为C∈直线AB,所以C∈α.
A
问题2:由平面的基本事实得到的推论
推论1:
图形表示:
(2)推论1可以简单地说成:直线和直线外一点确定一个平面.
推论2:
文字表示:经过两条相交直线,有且只有一个平面.
符号表示:l∩m=A 存在唯一的平面α,使l α,且m α
图形表示:
推论3:
文字表示:经过两条平行直线,有且只有一个平面
符号表示:l∥m 存在唯一的平面α,使l α,且m α
图形表示:
注:(1)推论2与推论3可以分别简单地说成“两条相交直线确定一个平面”,“两条平行直线确定一个平面”。
(2)推论2可以说明,三角形是平面图形,因此初中有关三角形全等,相似,以及前面我们学习的解三角形等结论,在空间中也是成立的。
(3)推论3可以说明平行四边形,梯形也是平面图形,初中有关平行四边形、梯形的判定与性质等结论,在空间中也成立.
【即时训练】
1.下列说法不正确的是( )
A.三角形是平面图形 B.一条直线和一个点可以确定一个平面
C.平行四边形是平面图形 D.初中学习的梯形的判断与性质等结论,在空间中仍然成立
B
2.经过空间任意三点作平面( )
A.只有一个 B.可作二个
C.可作无数多个 D.只有一个或有无数多个
答案:D 当三点在一条直线上时,过这三点的平面能作无数个;当三点不在同一条直线上时,过这三点的平面有且只有一个.
D
例1.证明:两两相交且不过同一个点的3条直线必在同一个平面内.
证明 在△ABD中,
因为E,H分别是AB,AD的中点,
所以EH∥BD.
同理FG∥BD,则EH∥FG.
故E,F,G,H四点共面.
小结:
1.证明三点共线的方法:先考虑两个平面的交线,再证有关的点都是这两个平面的公共点.或先由某两点作一直线,再证明其他点也在这条直线上.
2.证明点线共面的方法:先由有关元素确定一个基本平面,再证其他的点(或线)在这个平面内;或先由部分点线确定平面,再由其他点线确定平面,然后证明这些平面重合.注意对诸如“两平行直线确定一个平面”等依据的证明、记忆与运用.
3.证明多线共点的方法:先证两线共点,再证这个点在其他直线上,而“其他”直线往往归结为平面与平面的交线.
平面的基本事实与推论
核心知识
方法总结
易错提醒
核心素养
1会用数学语言描述点、线、面之间的位置关系
2.会证明推论1、推论2、推论3.
数学抽象:三种语言之间的相互转化
经过不在一直线上的三点,有且只有一平面
确定平面的条件
直观想象:点、线、面之间数学语言表示
一条直线上的两个点在平面内,那么直线
就在平面内
两个不重合的平面有一个公共点,那么它
们有且只有过该点的公共直线
证明 因为MN∩EF=Q,
所以Q∈直线MN,Q∈直线EF.
又因为M∈CD,N∈直线AB,CD 平面ABCD,
AB 平面ABCD直线,
所以M,N∈平面ABCD,所以MN 平面ABCD.
所以Q∈平面ABCD.同理,可得EF 平面ADD1A1,
所以Q∈平面ADD1A1.
又因为平面ABCD∩平面ADD1A1=AD,
所以Q∈直线AD,即D,A,Q三点共线.
(2)符号语言表示:平面ABD∩平面BDC=BD,
平面ABC∩平面ADC=AC.
图形表示如图②.
答案:D A是基本事实2,故A正确;
B是基本事实3,故B正确;
C是基本事实1,故C正确;
当l α,A∈l时,也有可能A∈α,如l∩α=A,故D不正确.
D
不能因为第一次飞翔遇到了乌云风暴,从此就怀疑没有蓝天彩霞。
