11.3.1 平行直线与异面直线 课件(共24张PPT)
文档属性
| 名称 | 11.3.1 平行直线与异面直线 课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 13:16:07 | ||
图片预览







文档简介
(共24张PPT)
11.3.1平行直线与异面直线
掌握平行公理、等角定理、异面直线的夹角以及空间四边形。
直观想象、逻辑推理:通过空间直线平行以及异面直线的夹角。
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
问题1:平行直线
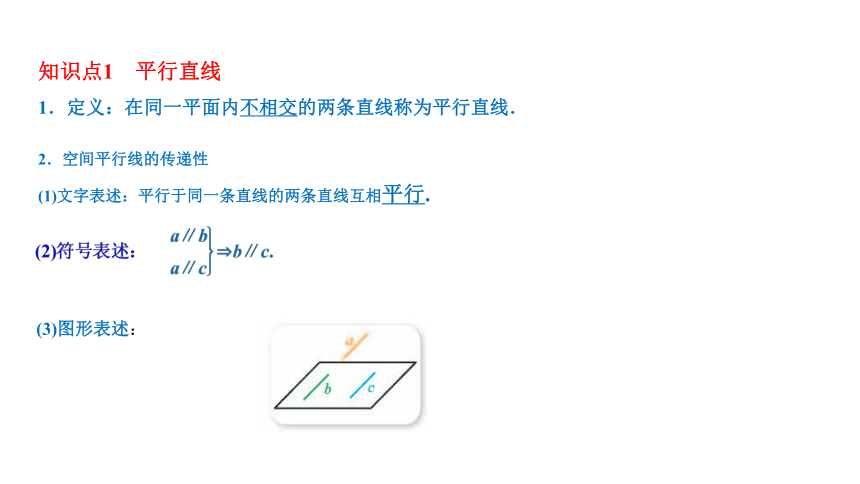
知识点1 平行直线
1.定义:在同一平面内不相交的两条直线称为平行直线.
2.空间平行线的传递性
(1)文字表述:平行于同一条直线的两条直线互相平行.
知识点1 平行直线
1.定义:在同一平面内不相交的两条直线称为平行直线.
2.空间平行线的传递性
(1)文字表述:平行于同一条直线的两条直线互相平行.
(3)图形表述:
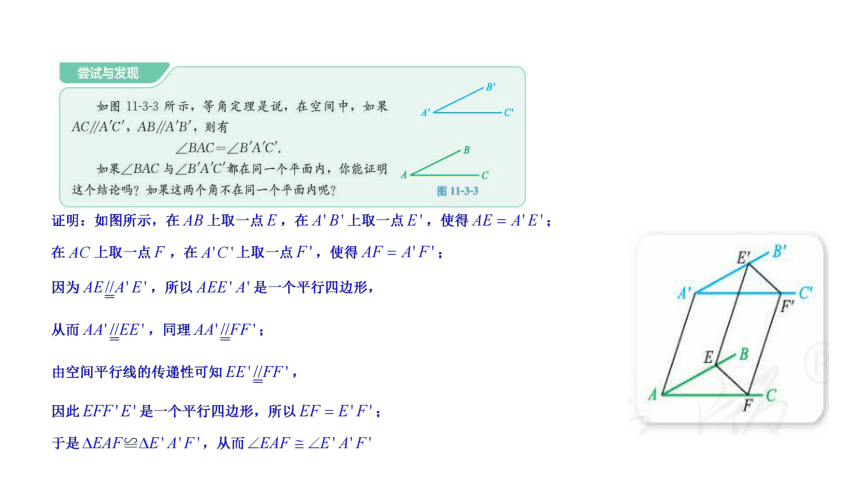
(2)由空间平行线的传递性可以得到空间中的等角定理
知识点2:等角定理
(1)文字表述:如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等.
(3)图形表述:
【即时训练】
1.直线a,b,c,d满足a∥b,b∥c,c∥d,则a与d的位置关系是________.
答案:平行 因为a∥b,b∥c,c∥d,所以由平行线的传递性可知a∥d.
答案:C 当∠B′A′C′与∠BAC开口方向相同时,∠B′A′C′=30°;当∠B′A′C′与∠BAC开口方向相反时,∠B′A′C′=150°.
平行
C
问题2:异面直线
我们知道,异面直线指的是空间中既不平行也不相交的直线,而且前面也从几何体中直观认识了异面直线。事实上,异面直线在实际生活中也是广泛存在的,如果所示.
知识点: 异面直线
(1)定义:两条直线异面,实际上也就是这两条直线不能同时在任何一个平面内.
(2)异面直线的画法:为了表示异面直线a,b不共面的特点,作图时,通常用一个或两个平面衬托,如图所示.
(3)判定方法:与一个平面相交于一点的直线与这个平面内不经过交点的直线异面.
答案:没有公共点的两条直线也可能是平行直线.
答案:不一定.异面直线是不同在任何一个平面内的直线.
问题3:空间四边形
知识点:空间四边形
1.定义:顺次连接不共面的4点所构成的图形称为空间四边形,其中4个点都是空间四边形的顶点,连接相邻顶点间的线段称为空间四边形的边,连接不相邻顶点间的线段称为空间四边形的对角线.
2.表示:用表示顶点的4个字母表示,如图所示为空间四边形ABCD,这个空间四边形的边为AB,BC,CD,DA,对角线为AC,BD.
【即时训练】
1.平行四边形、梯形等平面四边形是空间四边形?
答案: 空间四边形的4个点不共面,平面四边形不是空间四边形.
2.空间四边形是四面体吗?
答案: 不是.空间四边形可以看成由一个四面体的4条棱构成的图形.
核心知识
方法总结
易错提醒
核心素养
等角定理以及异面直线的夹角 (1)等角定理:如果一个角的两边与另一个角的两边分别平行且方向相同,那么这两个角相同。 (2)异面直线:空间中既不平行也不相交的直线
平行直线
异面直线
求异面直线所成的角
直观想象、逻辑推理:等角定理以及异面直线的夹角
直线与
直线平行
1.若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,
l是平面α与平面β的交线,则下列
命题正确的是 ( )
A.l至少与l1,l2中的一条相交
B.l与l1,l2都相交
C.l至多与l1,l2中的一条相交
D.l与l1,l2都不相交
B
3.已知E,E1分别是正方体ABCD-A1B1C1D1的棱AD,A1D1的中点.
求证:∠BEC=∠B1E1C1.
证明 证法一(反证法):假设AE和DF不是异面直线,则AE和DF共面,设过AE、DF的平面为β,若E、F重合,则E为BC的中点,所以AB=AC,与AB≠AC相矛盾.若E、F不重合,因为B∈EF,C∈EF,而EF β,
所以B∈β,C∈β,又A∈β,D∈β,
所以A、B、C、D四点共面,这与题设ABCD为空间四边形矛盾,综上可知,假设不成立,所以AE与DF为异面直线.
证法二(定理法):因为AB≠AC,AE⊥BC,F为BC的中点,所以E、F不重合,又A 平面BCD,E∈平面BCD,DF 平面BCD,E DF,所以AE与DF为异面直线.
白发无凭吾老矣!青春不再汝知乎?年将弱冠非童子,学不成名岂丈夫?
——俞良弼
11.3.1平行直线与异面直线
掌握平行公理、等角定理、异面直线的夹角以及空间四边形。
直观想象、逻辑推理:通过空间直线平行以及异面直线的夹角。
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
问题1:平行直线
知识点1 平行直线
1.定义:在同一平面内不相交的两条直线称为平行直线.
2.空间平行线的传递性
(1)文字表述:平行于同一条直线的两条直线互相平行.
知识点1 平行直线
1.定义:在同一平面内不相交的两条直线称为平行直线.
2.空间平行线的传递性
(1)文字表述:平行于同一条直线的两条直线互相平行.
(3)图形表述:
(2)由空间平行线的传递性可以得到空间中的等角定理
知识点2:等角定理
(1)文字表述:如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等.
(3)图形表述:
【即时训练】
1.直线a,b,c,d满足a∥b,b∥c,c∥d,则a与d的位置关系是________.
答案:平行 因为a∥b,b∥c,c∥d,所以由平行线的传递性可知a∥d.
答案:C 当∠B′A′C′与∠BAC开口方向相同时,∠B′A′C′=30°;当∠B′A′C′与∠BAC开口方向相反时,∠B′A′C′=150°.
平行
C
问题2:异面直线
我们知道,异面直线指的是空间中既不平行也不相交的直线,而且前面也从几何体中直观认识了异面直线。事实上,异面直线在实际生活中也是广泛存在的,如果所示.
知识点: 异面直线
(1)定义:两条直线异面,实际上也就是这两条直线不能同时在任何一个平面内.
(2)异面直线的画法:为了表示异面直线a,b不共面的特点,作图时,通常用一个或两个平面衬托,如图所示.
(3)判定方法:与一个平面相交于一点的直线与这个平面内不经过交点的直线异面.
答案:没有公共点的两条直线也可能是平行直线.
答案:不一定.异面直线是不同在任何一个平面内的直线.
问题3:空间四边形
知识点:空间四边形
1.定义:顺次连接不共面的4点所构成的图形称为空间四边形,其中4个点都是空间四边形的顶点,连接相邻顶点间的线段称为空间四边形的边,连接不相邻顶点间的线段称为空间四边形的对角线.
2.表示:用表示顶点的4个字母表示,如图所示为空间四边形ABCD,这个空间四边形的边为AB,BC,CD,DA,对角线为AC,BD.
【即时训练】
1.平行四边形、梯形等平面四边形是空间四边形?
答案: 空间四边形的4个点不共面,平面四边形不是空间四边形.
2.空间四边形是四面体吗?
答案: 不是.空间四边形可以看成由一个四面体的4条棱构成的图形.
核心知识
方法总结
易错提醒
核心素养
等角定理以及异面直线的夹角 (1)等角定理:如果一个角的两边与另一个角的两边分别平行且方向相同,那么这两个角相同。 (2)异面直线:空间中既不平行也不相交的直线
平行直线
异面直线
求异面直线所成的角
直观想象、逻辑推理:等角定理以及异面直线的夹角
直线与
直线平行
1.若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,
l是平面α与平面β的交线,则下列
命题正确的是 ( )
A.l至少与l1,l2中的一条相交
B.l与l1,l2都相交
C.l至多与l1,l2中的一条相交
D.l与l1,l2都不相交
B
3.已知E,E1分别是正方体ABCD-A1B1C1D1的棱AD,A1D1的中点.
求证:∠BEC=∠B1E1C1.
证明 证法一(反证法):假设AE和DF不是异面直线,则AE和DF共面,设过AE、DF的平面为β,若E、F重合,则E为BC的中点,所以AB=AC,与AB≠AC相矛盾.若E、F不重合,因为B∈EF,C∈EF,而EF β,
所以B∈β,C∈β,又A∈β,D∈β,
所以A、B、C、D四点共面,这与题设ABCD为空间四边形矛盾,综上可知,假设不成立,所以AE与DF为异面直线.
证法二(定理法):因为AB≠AC,AE⊥BC,F为BC的中点,所以E、F不重合,又A 平面BCD,E∈平面BCD,DF 平面BCD,E DF,所以AE与DF为异面直线.
白发无凭吾老矣!青春不再汝知乎?年将弱冠非童子,学不成名岂丈夫?
——俞良弼
