11.3.2 直线与平面平行 课件(共26张PPT)
文档属性
| 名称 | 11.3.2 直线与平面平行 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
11.3.2 直线与平面平行
一支笔所在的直线与一个作业本所在的平面,可能有几种位置关系?
思考
当门扇绕着门轴转动时, 转动的一边所在的直线与墙面所在的平面是怎样的位置关系呢?
1.理解直线与平面平行的判定定理.2.会用判定定理证明简单的线面平行的问题.3.了解直线与平面平行的性质定理的证明方法.4.掌握直线与平面平行的性质定理及其应用.
逻辑推理:转化为证明直线与直线平行判定
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
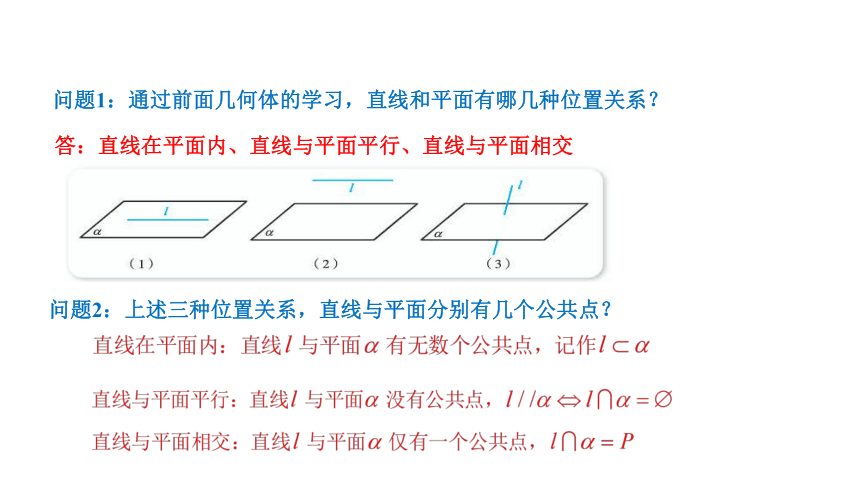
问题1:通过前面几何体的学习,直线和平面有哪几种位置关系?
答:直线在平面内、直线与平面平行、直线与平面相交
问题2:上述三种位置关系,直线与平面分别有几个公共点?
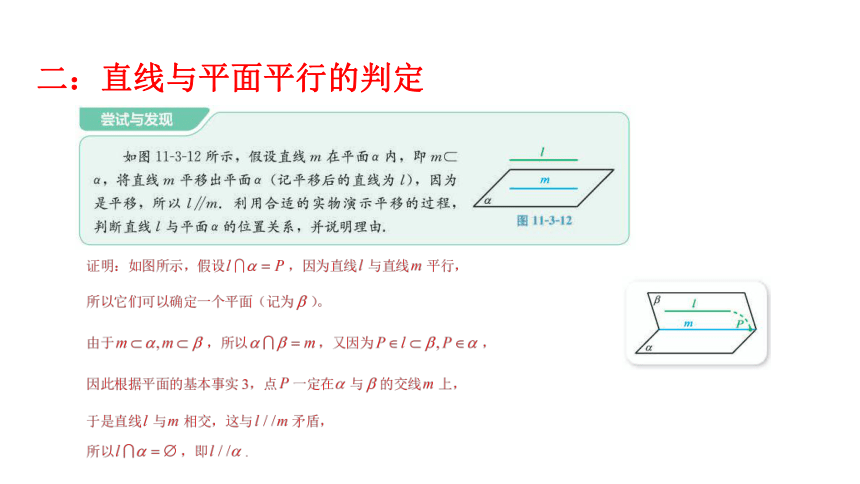
二:直线与平面平行的判定
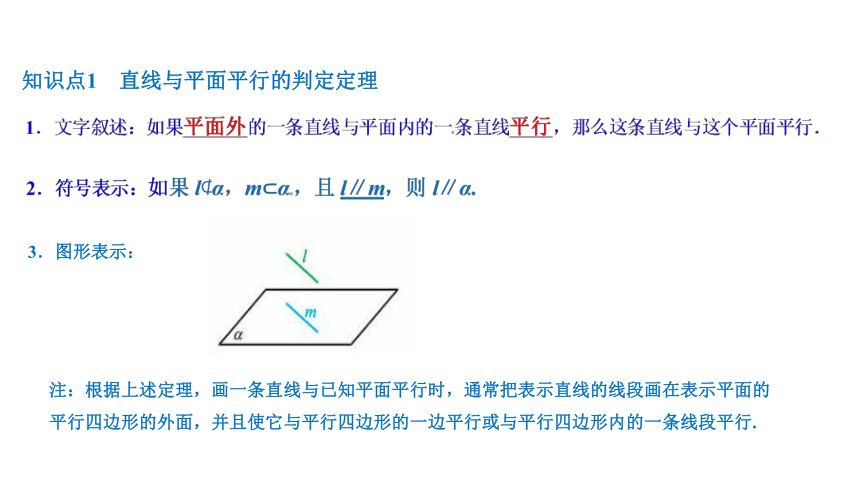
知识点1 直线与平面平行的判定定理
3.图形表示:
注:根据上述定理,画一条直线与已知平面平行时,通常把表示直线的线段画在表示平面的平行四边形的外面,并且使它与平行四边形的一边平行或与平行四边形内的一条线段平行.
4.作用:证明直线与平面平行.
利用线面平行的判定定理,以及棱柱的侧面都是平行四边形,可以证明棱柱一个底面上的边所在直线一定平行于另一个底面。
【即时训练】
1.思考辨析
(1)如果一条直线和一个平面内的另一条直线平行,那么这条直线和这个平面平行.
( )
(2)若直线l平行于平面α内的无数条直线,则l∥α.( )
(3)若直线a∥b,直线b α,则a∥α.( )
答案 D
×
D
×
×
证明 连接BD,交AC于O点,连接OE.
因为ABCD为矩形,
所以O为BD的中点.
又E为PD的中点,
所以OE∥PB.
又OE 平面AEC,PB 平面AEC,
所以PB∥平面AEC.
三.线面平行的性质定理
知识点2 直线与平面平行的性质定理
1.文字叙述:如果一条直线与一个平面平行,且经过这条直线的平面与这个平面相交,那么这条直线就与两平面的交线平行.
2.符号表示:如果l∥α,l β,α∩β=m,则l∥m.
3.图形表示:
4.作用:证明两直线平行.
证明:如果l∥α,l β,α∩β=m,则l∥m.
提示 不一定,因为还可能是异面直线.
2.如图,直线a∥平面α,直线a 平面β,平面α∩平面β=直线b,满足以上条件的平面β有多少个?直线a,b有什么位置关系?
提示 无数个,a∥b.
【变式练习】
求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行.
核心知识
直线与平面平行的性质定理
直线与平面平行的判定定理
方法总结
判定直线与平面平行
(1)关键是在平面内找一条直线与该直线平行
(2)方法是利用平行的传递性,通过中位线定理或平行四边形的性质
核心素养
注意性质定理中两条直线的位置
应用
直线与平面平行
易错提醒
逻辑推理:转化为证明直线与直线平行判定
1.如果平面外一条直线上有两点到这个平面的距离
相等.那么这条直线与这个平面的位置关系是( )
A.平行 B.相交
C.平行或相交 D.以上都不对
C
2.设AB,BC,CD是不在同一平面内的三条线段,则经
过它们中点的平面和直线AC的位置关系是( )
A.平行 B.相交
C.平行或相交 D.AC在此平面内
A
3.如图,在三棱锥S-ABC中,E,F分别是SB,SC上的点,且
EF∥平面ABC,则 ( )
A.EF与BC相交 B.EF∥BC
C.EF与BC异面 D.以上均有可能
B
α
4. 求证:如果过平面内一点的直线平行于与此平面平行的一条直线,那么这条直线在此平面内.
已知:l ∥α,点 P ∈α, P∈m 且 m∥l .
求证:m α.
β
m'
m
P
.
l
证明:设l与P确定的平面为β,
且α∩β=m′,因为l∥α,
所以l∥m′.又l∥m,m∩m′=P.
所以m′和m 重合 .所以m α.
【答案】A
A
我们应当努力奋斗,有所作为,这样,我们就可以说,我们没有虚度年华,并有可能在时间的沙滩上留下我们的足迹.
——拿破仑
11.3.2 直线与平面平行
一支笔所在的直线与一个作业本所在的平面,可能有几种位置关系?
思考
当门扇绕着门轴转动时, 转动的一边所在的直线与墙面所在的平面是怎样的位置关系呢?
1.理解直线与平面平行的判定定理.2.会用判定定理证明简单的线面平行的问题.3.了解直线与平面平行的性质定理的证明方法.4.掌握直线与平面平行的性质定理及其应用.
逻辑推理:转化为证明直线与直线平行判定
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
问题1:通过前面几何体的学习,直线和平面有哪几种位置关系?
答:直线在平面内、直线与平面平行、直线与平面相交
问题2:上述三种位置关系,直线与平面分别有几个公共点?
二:直线与平面平行的判定
知识点1 直线与平面平行的判定定理
3.图形表示:
注:根据上述定理,画一条直线与已知平面平行时,通常把表示直线的线段画在表示平面的平行四边形的外面,并且使它与平行四边形的一边平行或与平行四边形内的一条线段平行.
4.作用:证明直线与平面平行.
利用线面平行的判定定理,以及棱柱的侧面都是平行四边形,可以证明棱柱一个底面上的边所在直线一定平行于另一个底面。
【即时训练】
1.思考辨析
(1)如果一条直线和一个平面内的另一条直线平行,那么这条直线和这个平面平行.
( )
(2)若直线l平行于平面α内的无数条直线,则l∥α.( )
(3)若直线a∥b,直线b α,则a∥α.( )
答案 D
×
D
×
×
证明 连接BD,交AC于O点,连接OE.
因为ABCD为矩形,
所以O为BD的中点.
又E为PD的中点,
所以OE∥PB.
又OE 平面AEC,PB 平面AEC,
所以PB∥平面AEC.
三.线面平行的性质定理
知识点2 直线与平面平行的性质定理
1.文字叙述:如果一条直线与一个平面平行,且经过这条直线的平面与这个平面相交,那么这条直线就与两平面的交线平行.
2.符号表示:如果l∥α,l β,α∩β=m,则l∥m.
3.图形表示:
4.作用:证明两直线平行.
证明:如果l∥α,l β,α∩β=m,则l∥m.
提示 不一定,因为还可能是异面直线.
2.如图,直线a∥平面α,直线a 平面β,平面α∩平面β=直线b,满足以上条件的平面β有多少个?直线a,b有什么位置关系?
提示 无数个,a∥b.
【变式练习】
求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行.
核心知识
直线与平面平行的性质定理
直线与平面平行的判定定理
方法总结
判定直线与平面平行
(1)关键是在平面内找一条直线与该直线平行
(2)方法是利用平行的传递性,通过中位线定理或平行四边形的性质
核心素养
注意性质定理中两条直线的位置
应用
直线与平面平行
易错提醒
逻辑推理:转化为证明直线与直线平行判定
1.如果平面外一条直线上有两点到这个平面的距离
相等.那么这条直线与这个平面的位置关系是( )
A.平行 B.相交
C.平行或相交 D.以上都不对
C
2.设AB,BC,CD是不在同一平面内的三条线段,则经
过它们中点的平面和直线AC的位置关系是( )
A.平行 B.相交
C.平行或相交 D.AC在此平面内
A
3.如图,在三棱锥S-ABC中,E,F分别是SB,SC上的点,且
EF∥平面ABC,则 ( )
A.EF与BC相交 B.EF∥BC
C.EF与BC异面 D.以上均有可能
B
α
4. 求证:如果过平面内一点的直线平行于与此平面平行的一条直线,那么这条直线在此平面内.
已知:l ∥α,点 P ∈α, P∈m 且 m∥l .
求证:m α.
β
m'
m
P
.
l
证明:设l与P确定的平面为β,
且α∩β=m′,因为l∥α,
所以l∥m′.又l∥m,m∩m′=P.
所以m′和m 重合 .所以m α.
【答案】A
A
我们应当努力奋斗,有所作为,这样,我们就可以说,我们没有虚度年华,并有可能在时间的沙滩上留下我们的足迹.
——拿破仑
