9.1.1正弦定理 课件(共41张PPT)
文档属性
| 名称 | 9.1.1正弦定理 课件(共41张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 13:19:29 | ||
图片预览






文档简介
(共41张PPT)
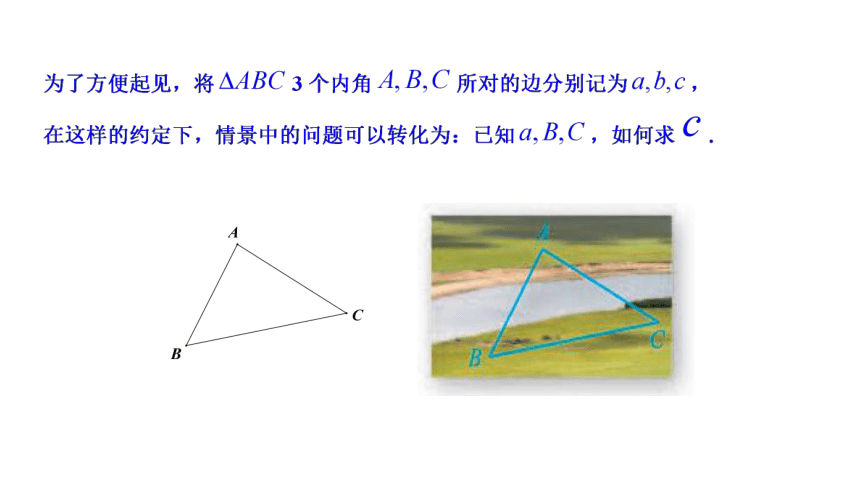
9.1.1 正弦定理
1. 掌握正弦定理的内容;(重点)
2. 掌握正弦定理的证明方法;
3. 会运用正弦定理与三角形内角和定理解斜三角形的两类基本问题. (难点)
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
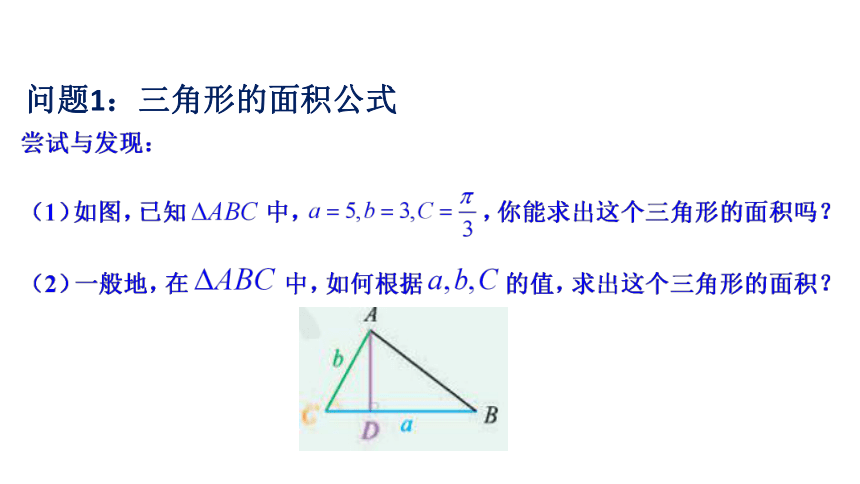
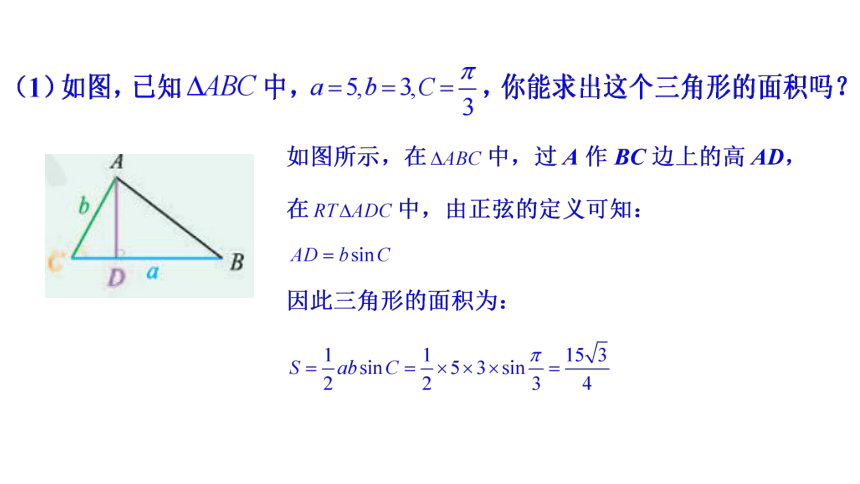
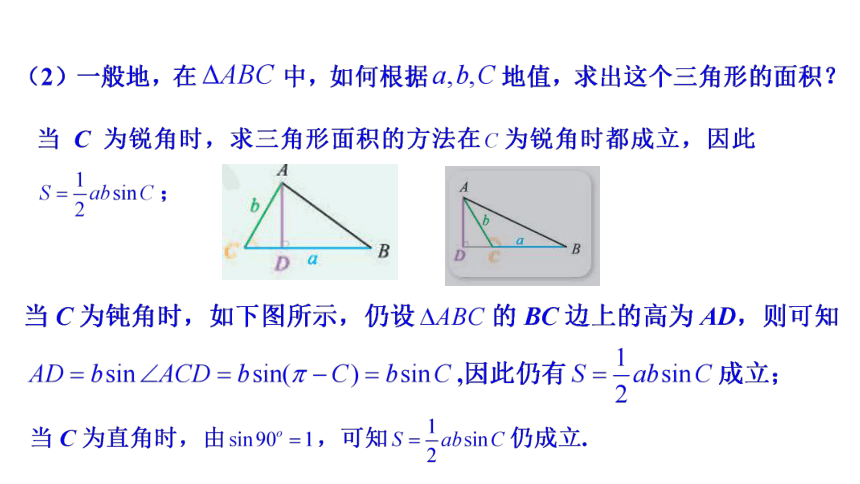
问题1:三角形的面积公式
问题2:正弦定理
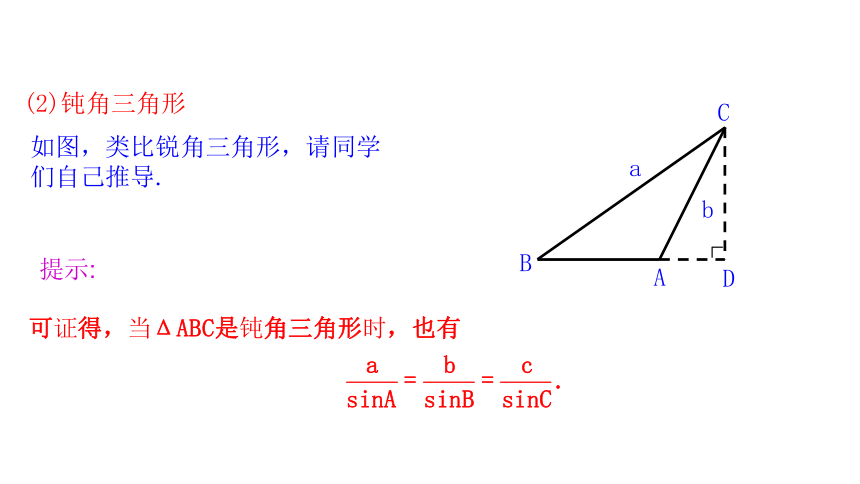
(2)钝角三角形
如图,类比锐角三角形,请同学们自己推导.
提示:
A
C
a
b
B
D
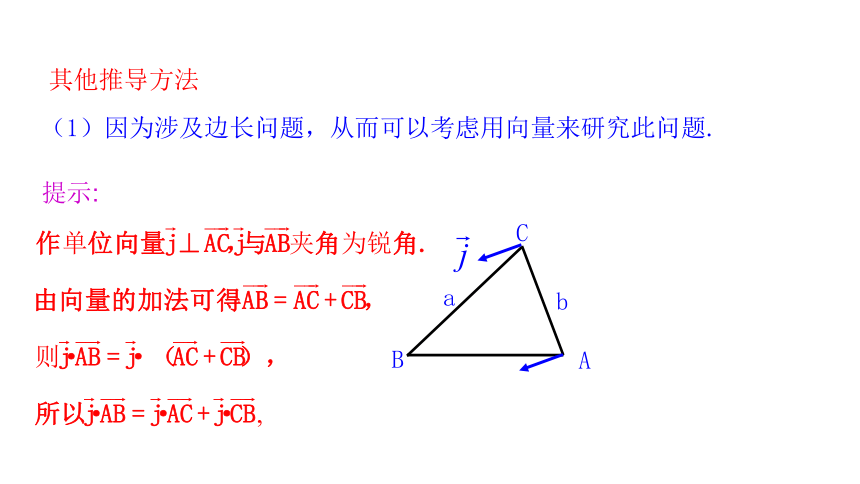
其他推导方法
(1)因为涉及边长问题,从而可以考虑用向量来研究此问题.
提示:
C
b
a
A
B
(2)外接圆法
提示:
B`
A
B
C
b
O
C
A
B
b
O
A`
a
a
c
c
【即时训练】
D
问题3:利用正弦定理和三角形内角和定理,解决三角形
5
核心素养
易错提醒
方法总结
核心
知识
1.正弦定理
2 推论.
3.利用正弦定理解三角形.
已知两角及一边解三角形
(1)若所给边是已知角的对边时,可由正弦定理求另一边,再由三角形内角和定理求出第三个角,最后由正弦定理求第三边.
(2)若所给边不是已知角的对边时,先由三角形内角和定理求第三个角,再由正弦定理求另外两边.
已知两边及一边的对角解三角形
(1)由正弦定理求出另一边对角的正弦值.
(2)如果已知的角为大边所对的角时,由正弦值可求锐角即为另一边所对的角.
(3)如果已知的角为小边所对的角时,要分类讨论.
已知两边和其中一边所对角解三角形时可能会出现无解、一解、两解的情况.
注意“大边对大角、大角对大边”.
1.数学抽象:正弦定理及其变形、三角形面积公式.
2.逻辑推理:用正弦定理及其变形解决相关问题.
3.数学运算:解三角形.
D
C
D
【
解析
】
因为
í
ì
A
:
B
:
C
=
3
:
2
:
1
A
+
B
+
C
=
180°
,
所以
A
=
90°
,
B
=
60°
,
C
=
30°.
a
:
b
:
c
=
sin
A
:
sin
B
:
sin
C
=
1
:
3
2
:
1
2
=
2
:
3
:
1.
所以
B
地球上一切美丽的东西都来源于太阳,而一切美好的东西都来源于人.
——普朗克
9.1.1 正弦定理
1. 掌握正弦定理的内容;(重点)
2. 掌握正弦定理的证明方法;
3. 会运用正弦定理与三角形内角和定理解斜三角形的两类基本问题. (难点)
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
问题1:三角形的面积公式
问题2:正弦定理
(2)钝角三角形
如图,类比锐角三角形,请同学们自己推导.
提示:
A
C
a
b
B
D
其他推导方法
(1)因为涉及边长问题,从而可以考虑用向量来研究此问题.
提示:
C
b
a
A
B
(2)外接圆法
提示:
B`
A
B
C
b
O
C
A
B
b
O
A`
a
a
c
c
【即时训练】
D
问题3:利用正弦定理和三角形内角和定理,解决三角形
5
核心素养
易错提醒
方法总结
核心
知识
1.正弦定理
2 推论.
3.利用正弦定理解三角形.
已知两角及一边解三角形
(1)若所给边是已知角的对边时,可由正弦定理求另一边,再由三角形内角和定理求出第三个角,最后由正弦定理求第三边.
(2)若所给边不是已知角的对边时,先由三角形内角和定理求第三个角,再由正弦定理求另外两边.
已知两边及一边的对角解三角形
(1)由正弦定理求出另一边对角的正弦值.
(2)如果已知的角为大边所对的角时,由正弦值可求锐角即为另一边所对的角.
(3)如果已知的角为小边所对的角时,要分类讨论.
已知两边和其中一边所对角解三角形时可能会出现无解、一解、两解的情况.
注意“大边对大角、大角对大边”.
1.数学抽象:正弦定理及其变形、三角形面积公式.
2.逻辑推理:用正弦定理及其变形解决相关问题.
3.数学运算:解三角形.
D
C
D
【
解析
】
因为
í
ì
A
:
B
:
C
=
3
:
2
:
1
A
+
B
+
C
=
180°
,
所以
A
=
90°
,
B
=
60°
,
C
=
30°.
a
:
b
:
c
=
sin
A
:
sin
B
:
sin
C
=
1
:
3
2
:
1
2
=
2
:
3
:
1.
所以
B
地球上一切美丽的东西都来源于太阳,而一切美好的东西都来源于人.
——普朗克
