9.2 正弦定理与余弦定理的应用 课件(共32张PPT)
文档属性
| 名称 | 9.2 正弦定理与余弦定理的应用 课件(共32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 13:24:14 | ||
图片预览










文档简介
(共32张PPT)
9.2正弦定理与余弦定理的应用
有这样一个问题:遥不可及的月球离地球究竟有多远呢?在古代,天文学家没有先进的仪器就已经估算出了两者的距离,他们是用什么神奇的方法探索到这个奥秘的呢?
我们知道,对于未知的距离、高度等,存在着许多可供选择的测量方案,比如可以应用全等三角形、相似三角形的方法,或借助解直角三角形等不同的方法来解决,但由于在实际测量问题的真实背景下,某些方法却不能实施.如因为没有足够的空间,不能用全等三角形的方法来测量,所以,有些方法会有局限性. 上面介绍的问题就是用以前的方法所不能解决的.
今天我们开始学习正弦定理、余弦定理在科学实践中的重要应用,首先研究如何测量距离.
能够运用正弦定理、余弦定理等知识和方法解决一些有关测量距离的实际问题,了解常用的测量相关术语.(重点、难点)
利用正弦定理、余弦定理解决实际生活中的距离问题, 培养学生运用图形、数学符号表达题意和应用数学建模解决实际问题的能力。
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
复习回顾:
问题1:测量相关术语
1.实际问题中的有关术语、名称
(1)仰角和俯角
测量时,以水平线为基准,视线在水平线上方所成的角叫做___________;视线在水平线下方所成的角叫做___________.
(如图)
仰角
俯角
(2)方向角与方位角
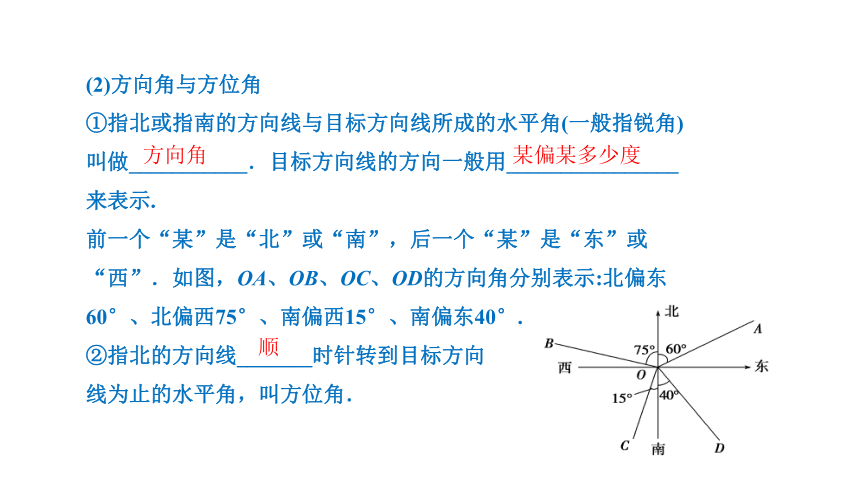
①指北或指南的方向线与目标方向线所成的水平角(一般指锐角)叫做___________.目标方向线的方向一般用________________来表示.
前一个“某”是“北”或“南”,后一个“某”是“东”或“西”.如图,OA、OB、OC、OD的方向角分别表示:北偏东60°、北偏西75°、南偏西15°、南偏东40°.
②指北的方向线_______时针转到目标方向
线为止的水平角,叫方位角.
方向角
某偏某多少度
顺
(3)水平距离、垂直距离、坡面距离、坡度和坡角
如图所示,BC代表水平距离,AC代表垂直距离,AB代表坡面距离.
坡角
问题2:高度问题
【解题方法】
解决测量高度问题时要注意的两个问题
(1)要清楚仰角与俯角的区别及联系.
(2)测量底部不能到达的建筑物的高度问题,一般是转化为直角三角形模型,但在某些情况下,仍需根据正、余弦定理解决.
问题1:距离问题
【解题方法】
正弦定理与余弦定理交汇求距离的两个关键点
(1)画示意图,弄清题目条件.
根据题意画图研究问题中所涉及的三角形,它的哪些元素是已知的,哪些元素是未知的.
(2)选准入手点.
找出已知边长的三角形,结合已知条件选准“可解三角形”,并判断是选用正弦定理,还是选用余弦定理来求解.
问题3:几何类问题
【解题方法】
几何类问题的证明与求解方法
(1)将平面图形合理地分解为若干三角形.
(2)注意直角三角形、等腰三角形、等边三角形中的角角、边边关系、三角形外角及内角关系以及三角形内角和定理.
(3)将问题归结到一个或几个三角形中,结合三角恒等变换,合理地运用正、余弦定理求解.
余弦定理、正弦定理应用举例
——距离问题
1.数学抽象:常用的测量相关术语;
2.逻辑推理:将实际问题转化为数学问题;
3.数学运算:利用余弦定理、正弦定理求距离;
4.数学模型:在适当的三角形中解距离。
核心知识
核心素养
方法总结
易错提醒
核心素养
1 解决应用题的思想方法
把实际问题转化为数学问题
2.求解三角形应用题的一般步骤
(1)审题(分析题意,根据题意,画出示意图)
(2)建模(将实际问题转化为解斜三角形的数学问题)
(3)求模(正确运用正、余弦定理求解)
(4)还原。
分析转化
实际问题
解三角形问题
数学结论
检验
数学问题
1.选定或确定所求量所在的三角形,若其他量已知,则直接求解
2.若有未知量,则把未知量放在另一确定三角形中求解
A
75°
4.一艘船以32.2 n mile / h的速度向正北航行.在A处看灯塔S在船的北偏东20o的方向,30 min后航行到B处,在B处看灯塔在船的北偏东65o的方向,已知距离此灯塔6.5 n mile 以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?
烈火试真金,逆境试强者.
——塞内加
9.2正弦定理与余弦定理的应用
有这样一个问题:遥不可及的月球离地球究竟有多远呢?在古代,天文学家没有先进的仪器就已经估算出了两者的距离,他们是用什么神奇的方法探索到这个奥秘的呢?
我们知道,对于未知的距离、高度等,存在着许多可供选择的测量方案,比如可以应用全等三角形、相似三角形的方法,或借助解直角三角形等不同的方法来解决,但由于在实际测量问题的真实背景下,某些方法却不能实施.如因为没有足够的空间,不能用全等三角形的方法来测量,所以,有些方法会有局限性. 上面介绍的问题就是用以前的方法所不能解决的.
今天我们开始学习正弦定理、余弦定理在科学实践中的重要应用,首先研究如何测量距离.
能够运用正弦定理、余弦定理等知识和方法解决一些有关测量距离的实际问题,了解常用的测量相关术语.(重点、难点)
利用正弦定理、余弦定理解决实际生活中的距离问题, 培养学生运用图形、数学符号表达题意和应用数学建模解决实际问题的能力。
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
复习回顾:
问题1:测量相关术语
1.实际问题中的有关术语、名称
(1)仰角和俯角
测量时,以水平线为基准,视线在水平线上方所成的角叫做___________;视线在水平线下方所成的角叫做___________.
(如图)
仰角
俯角
(2)方向角与方位角
①指北或指南的方向线与目标方向线所成的水平角(一般指锐角)叫做___________.目标方向线的方向一般用________________来表示.
前一个“某”是“北”或“南”,后一个“某”是“东”或“西”.如图,OA、OB、OC、OD的方向角分别表示:北偏东60°、北偏西75°、南偏西15°、南偏东40°.
②指北的方向线_______时针转到目标方向
线为止的水平角,叫方位角.
方向角
某偏某多少度
顺
(3)水平距离、垂直距离、坡面距离、坡度和坡角
如图所示,BC代表水平距离,AC代表垂直距离,AB代表坡面距离.
坡角
问题2:高度问题
【解题方法】
解决测量高度问题时要注意的两个问题
(1)要清楚仰角与俯角的区别及联系.
(2)测量底部不能到达的建筑物的高度问题,一般是转化为直角三角形模型,但在某些情况下,仍需根据正、余弦定理解决.
问题1:距离问题
【解题方法】
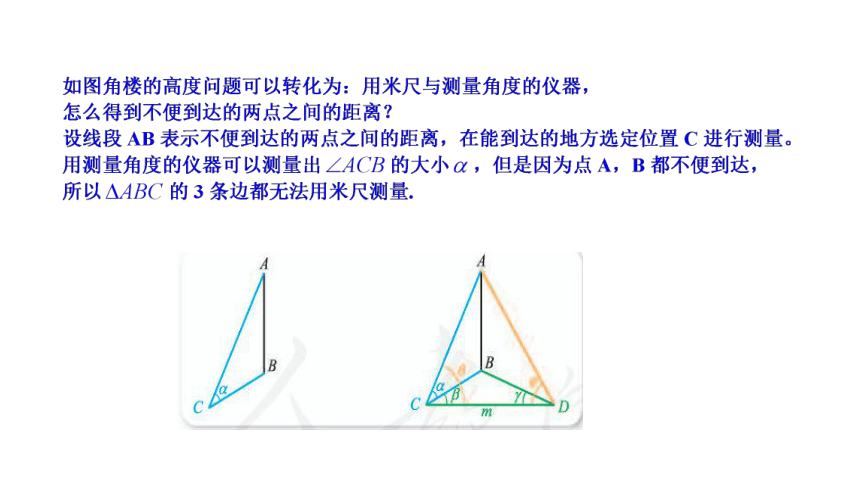
正弦定理与余弦定理交汇求距离的两个关键点
(1)画示意图,弄清题目条件.
根据题意画图研究问题中所涉及的三角形,它的哪些元素是已知的,哪些元素是未知的.
(2)选准入手点.
找出已知边长的三角形,结合已知条件选准“可解三角形”,并判断是选用正弦定理,还是选用余弦定理来求解.
问题3:几何类问题
【解题方法】
几何类问题的证明与求解方法
(1)将平面图形合理地分解为若干三角形.
(2)注意直角三角形、等腰三角形、等边三角形中的角角、边边关系、三角形外角及内角关系以及三角形内角和定理.
(3)将问题归结到一个或几个三角形中,结合三角恒等变换,合理地运用正、余弦定理求解.
余弦定理、正弦定理应用举例
——距离问题
1.数学抽象:常用的测量相关术语;
2.逻辑推理:将实际问题转化为数学问题;
3.数学运算:利用余弦定理、正弦定理求距离;
4.数学模型:在适当的三角形中解距离。
核心知识
核心素养
方法总结
易错提醒
核心素养
1 解决应用题的思想方法
把实际问题转化为数学问题
2.求解三角形应用题的一般步骤
(1)审题(分析题意,根据题意,画出示意图)
(2)建模(将实际问题转化为解斜三角形的数学问题)
(3)求模(正确运用正、余弦定理求解)
(4)还原。
分析转化
实际问题
解三角形问题
数学结论
检验
数学问题
1.选定或确定所求量所在的三角形,若其他量已知,则直接求解
2.若有未知量,则把未知量放在另一确定三角形中求解
A
75°
4.一艘船以32.2 n mile / h的速度向正北航行.在A处看灯塔S在船的北偏东20o的方向,30 min后航行到B处,在B处看灯塔在船的北偏东65o的方向,已知距离此灯塔6.5 n mile 以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?
烈火试真金,逆境试强者.
——塞内加
