10.1.1 复数的概念 课件(共25张PPT)
文档属性
| 名称 | 10.1.1 复数的概念 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 13:26:48 | ||
图片预览








文档简介
(共25张PPT)
10.1复数及其几何意义
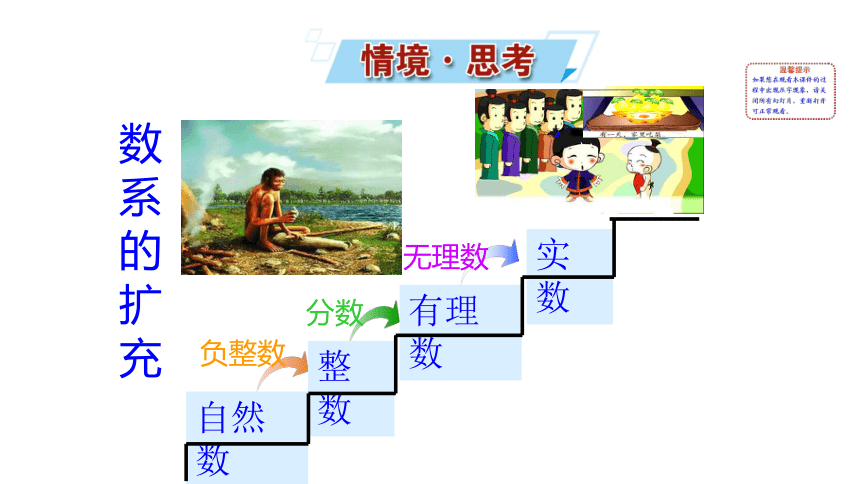
自然数
整数
有理数
实数
数 系 的 扩 充
负整数
分数
无理数
自然数
整数
有理数
实数
数 系 的 扩 充
负整数
分数
无理数
1.了解数系的扩充过程;2.理解复数的基本概念以及复数相等的充要
条件;3.了解复数的代数表示法;4.掌握复数集与实数集之间的关系.
培养学生数学抽象、数学运算、逻辑推理的能力.
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
正数与负数,
有理数与无理数,
都是具有“实际意义的量”,
称之为“实数”,构成实数系统.
实数系统是一个没有缝隙的连续系统.
实数集能否继续扩充呢
探究点1 数系的扩充
情境与问题
i的引入
尝试与发现
引入一个新数 i ,把 i 叫做虚数单位,并且规定:
(1)i 2 1;
(2)实数与i可以进行加法和乘法运算:
实数a与数i相加记为:a+i
实数b与数i相乘记为:bi ,并规定0 i =0
实数a与 bi相加记为:a+bi
(3)实数与 i 进行四则运算时,原有的加法、乘法运算律仍然成立.
尝试与发现
复数的概念
定义:把形如a+bi(a,b∈R)的数叫做复数。通常用字母 z 表示.
全体复数组成的集合叫做复数集,记作C。
其中 i 为虚数单位。
实部
虚部
复数的概念
变式训练1:
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
两个复数相等
注意:一般对两个复数只能说相等或不相等;不能比较大小。
已知(x+y)+(x-2y)i=(2x-5)+(3x+y)i,求实数x,y的值.
变式训练1:
变式训练2:
1. 虚数单位i的引入,数系的扩充;
2. 复数有关概念:
复数的代数形式:
复数的实部、虚部
复数相等
复数的分类
数系的扩充和复数的概念
核心知识
方法总结
核心素养
易错提醒
1.数系的扩充.
2. 复数有关的概念
(1)判断复数是实数、虚数或者纯虚数:①保证复数的实部、虚部均有意义.②根据分类的标准,列出实部、虚部应满足的关系式再求解.
(2)复数相等求参数的步骤:分别确定两个复数的实部与虚部,
利用实部与实部、虚部与虚部分别相等,列方程组求解.
(1)两个复数不全是实数,就不能比较大小.
(2)一个数的平方非负在实数范围内是真命题,在复数范围内是假命题.
(3)对于复数实部、虚部的确定不但要把复数化为a+bi的形式,更要
注意这里a,b均为实数时,才能确定复数的实、虚部.
1.数学抽象:复数及相关概念.
2.逻辑推理:复数的分类.
3.数学运算:复数相等求参数.
1、复数的代数形式.
2、复数的实部、虚部.
3、虚数、纯虚数.
4、复数相等.
1.a=0是复数a+bi(a,b∈R)为纯虚数的( )
A.必要条件 B.充分条件
C.充要条件 D.非必要非充分条件
A
C
【解析】选C.因为a-1+(a-2)i为实数,所以a-2=0,a=2.
2.(2020·浙江高考)已知a∈R,若a-1+(a-2)i(i为虚数单位)
是实数,则a=( )
A.1 B.-1 C.2 D.-2
3.我们已知i是-1的一个平方根,即方程x2=-1的一
个根,那么方程x2=-1的另一个根是________.
-i
4.复数i2 (1+i)的实部是________.
-1
解 根据复数相等的定义,得方程组
解得
-3
用心智的全部力量,来选择我们应遵循的道路.
———笛卡儿
10.1复数及其几何意义
自然数
整数
有理数
实数
数 系 的 扩 充
负整数
分数
无理数
自然数
整数
有理数
实数
数 系 的 扩 充
负整数
分数
无理数
1.了解数系的扩充过程;2.理解复数的基本概念以及复数相等的充要
条件;3.了解复数的代数表示法;4.掌握复数集与实数集之间的关系.
培养学生数学抽象、数学运算、逻辑推理的能力.
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
正数与负数,
有理数与无理数,
都是具有“实际意义的量”,
称之为“实数”,构成实数系统.
实数系统是一个没有缝隙的连续系统.
实数集能否继续扩充呢
探究点1 数系的扩充
情境与问题
i的引入
尝试与发现
引入一个新数 i ,把 i 叫做虚数单位,并且规定:
(1)i 2 1;
(2)实数与i可以进行加法和乘法运算:
实数a与数i相加记为:a+i
实数b与数i相乘记为:bi ,并规定0 i =0
实数a与 bi相加记为:a+bi
(3)实数与 i 进行四则运算时,原有的加法、乘法运算律仍然成立.
尝试与发现
复数的概念
定义:把形如a+bi(a,b∈R)的数叫做复数。通常用字母 z 表示.
全体复数组成的集合叫做复数集,记作C。
其中 i 为虚数单位。
实部
虚部
复数的概念
变式训练1:
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
两个复数相等
注意:一般对两个复数只能说相等或不相等;不能比较大小。
已知(x+y)+(x-2y)i=(2x-5)+(3x+y)i,求实数x,y的值.
变式训练1:
变式训练2:
1. 虚数单位i的引入,数系的扩充;
2. 复数有关概念:
复数的代数形式:
复数的实部、虚部
复数相等
复数的分类
数系的扩充和复数的概念
核心知识
方法总结
核心素养
易错提醒
1.数系的扩充.
2. 复数有关的概念
(1)判断复数是实数、虚数或者纯虚数:①保证复数的实部、虚部均有意义.②根据分类的标准,列出实部、虚部应满足的关系式再求解.
(2)复数相等求参数的步骤:分别确定两个复数的实部与虚部,
利用实部与实部、虚部与虚部分别相等,列方程组求解.
(1)两个复数不全是实数,就不能比较大小.
(2)一个数的平方非负在实数范围内是真命题,在复数范围内是假命题.
(3)对于复数实部、虚部的确定不但要把复数化为a+bi的形式,更要
注意这里a,b均为实数时,才能确定复数的实、虚部.
1.数学抽象:复数及相关概念.
2.逻辑推理:复数的分类.
3.数学运算:复数相等求参数.
1、复数的代数形式.
2、复数的实部、虚部.
3、虚数、纯虚数.
4、复数相等.
1.a=0是复数a+bi(a,b∈R)为纯虚数的( )
A.必要条件 B.充分条件
C.充要条件 D.非必要非充分条件
A
C
【解析】选C.因为a-1+(a-2)i为实数,所以a-2=0,a=2.
2.(2020·浙江高考)已知a∈R,若a-1+(a-2)i(i为虚数单位)
是实数,则a=( )
A.1 B.-1 C.2 D.-2
3.我们已知i是-1的一个平方根,即方程x2=-1的一
个根,那么方程x2=-1的另一个根是________.
-i
4.复数i2 (1+i)的实部是________.
-1
解 根据复数相等的定义,得方程组
解得
-3
用心智的全部力量,来选择我们应遵循的道路.
———笛卡儿
