10.1.2 复数的几何意义 课件(共26张PPT)
文档属性
| 名称 | 10.1.2 复数的几何意义 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
10.1.2复数的几何意义
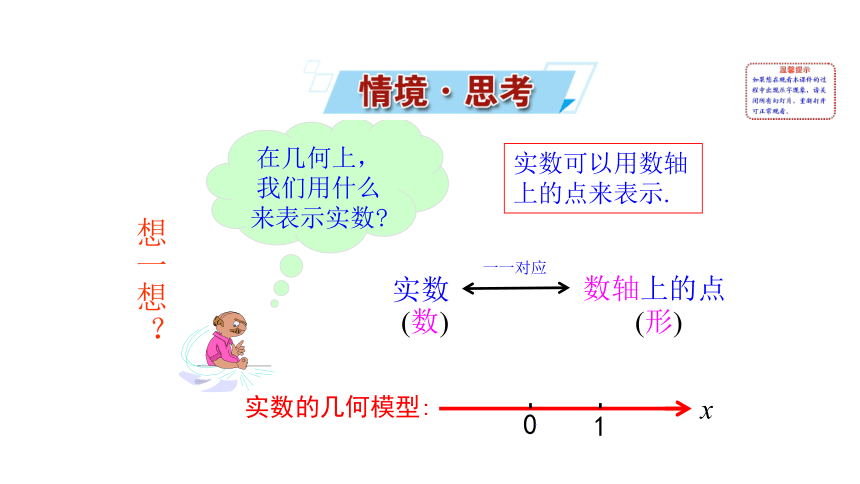
在几何上,我们用什么来表示实数
实数可以用数轴上的点来表示.
实数
数轴上的点
(形)
(数)
一一对应
想一想?
x
0
1
实数的几何模型:
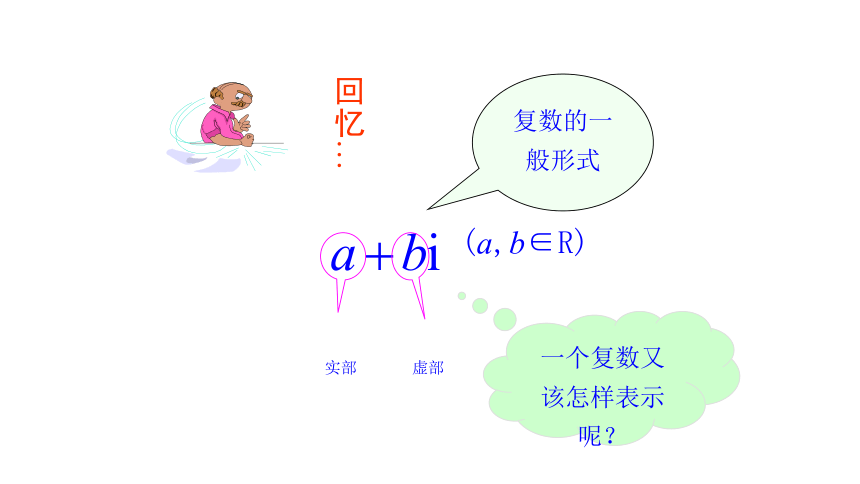
复数的一般形式
一个复数又该怎样表示呢?
回忆…
实部
虚部
(a,b∈R)
1.类比实数的几何意义思考复数的几何意义.
2.明确复数的两种几何意义.
3.了解复数模的意义,和共轭复数的概念。
体会数学抽象及数学运算素养,培养数形结合的直观想象的能力。
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
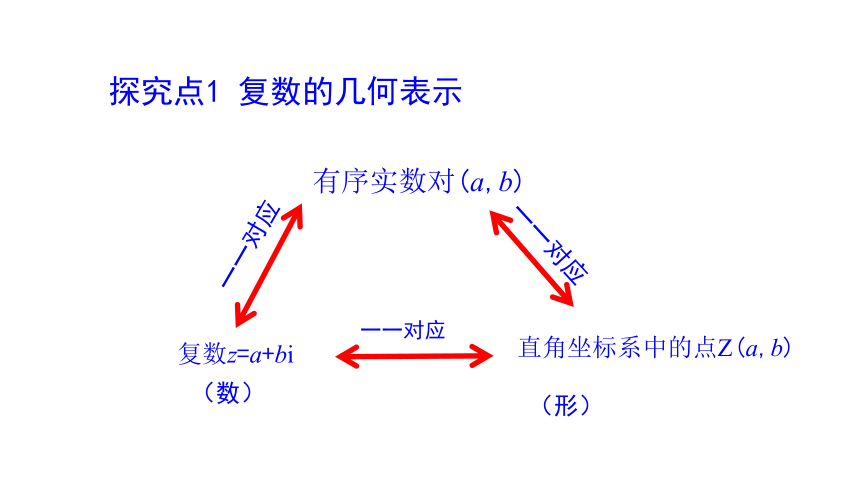
复数z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
(数)
(形)
一一对应
一一对应
一一对应
探究点1 复数的几何表示
x
y
0
Z(a,b)
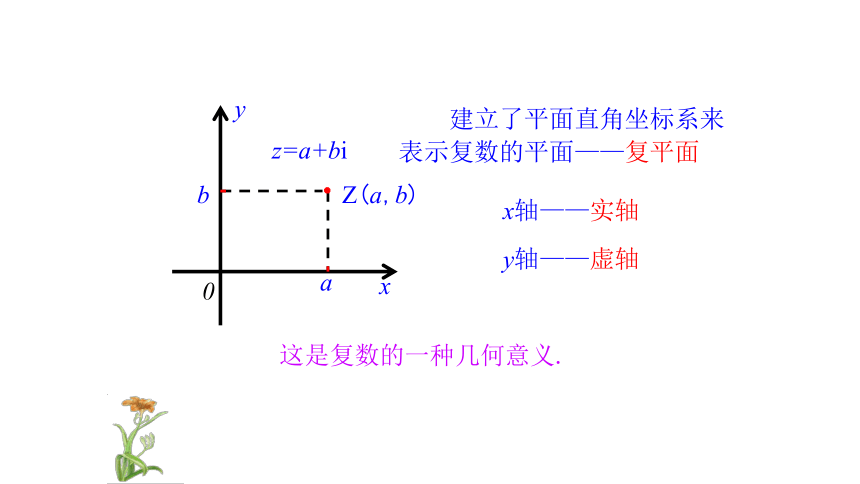
建立了平面直角坐标系来表示复数的平面——复平面
x轴——实轴
y轴——虚轴
a
b
z=a+bi
这是复数的一种几何意义.
A.在复平面内,对应于实数的点都在实轴上
B.在复平面内,对应于纯虚数的点都在虚轴上
C.在复平面内,实轴上的点所对应的复数都是实数
D.在复平面内,虚轴上的点所对应的复数都是纯虚数
下列命题中的假命题是( )
D
【即时训练】
【解题关键】虚轴上的点除原点外都表示纯虚数。
实数绝对值的几何意义:
复数的模其实是实数绝对值概念的推广
x
O
A
a
|a| = |OA|
实数a在数轴上所对应的点A到原点O的距离.
x
O
z=a+bi
y
|z|=|OZ|
复数的模
复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离.
的几何意义:
Z(a,b)
注意 a+bi 与 a-bi 两复数的特点.
定义:实部相等,虚部互为相反数的两个复数叫做互为共轭复数.
复数 z=a+bi 的共轭复数记作
x
O
z=a+bi
y
Z(a,-b)
Z(a,b)
z=a-bi
在复平面内表示两个共轭复数的点,
关于实轴对称,并且他们的模相等
【即时训练】
【变式训练】
【变式1】已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围.
表示复数的点所在象限的问题
复数的实部与虚部所满足的不等式组的问题
转化
(几何问题)
(代数问题)
一种重要的数学思想:数形结合思想
复数的
几何意义
方法总结
核心知识
易错提醒
核心素养
(1)已知复平面内对应的点满足的条件求参数取值范围时,可根据
复数与点的对应关系,通过解方程(组)或不等式(组)求解.
(2)根据|a+bi|= 可把复数模的问题转化为实数问题解决.
(3)根据|z|=| |,可把复数模的问题转化为向量模的问题解决.
1.原点确定的复数是实数0,除了原点外,虚轴上的点都表示纯虚数.
2.复数的模是非负实数,因此复数的模可以比较大小.
1.数学抽象:复平面及复数的几何意义的理解.
2.逻辑推理:根据平面与向量的关系推出复数与向量的一一对应及复数模公式.
3.数学运算:根据复数与复平面的点一一对应求参数和求复数的模.
4.数学建模:根据复数的代数形式,数形结合,多方位了解复数的几何意义.
1. 复平面.
2. 复数与点的对应.
3. 复数与向量的对应.
4. 复数的模.
1.“a=0”是“复数a+bi (a , b∈R)所对应的点
在虚轴上”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.不充分不必要条件
C
D
3. 在复平面内,描出下列各复数的点:
x
y
O
⑴ 2+5i;
⑵ -3+2i;
⑶ 2-4i;
⑷-3-i;
⑸ 5;
⑹ -3i.
x
y
O
⑵
⑷
⑶
⑸
⑴
⑹
解析:
⑴ 2+5i;
⑵ -3+2i;
⑶ 2-4i;
⑷-3-i;
⑸ 5;
⑹ -3i.
解
析
:
因为
z
为纯虚数,
所以
设
z
=
a
i
(
a
∈
R
且
a
≠
0)
,又
|
-
1
+
i
|
=
2
,由
|
z
-
1|
=
|
-
1
+
i
|
,
得
a
2
+
1
=
2
,解得
a
=
±
1
,
所以
z
=
±
i.
自己活着,就是为了使别人活得更美好。
10.1.2复数的几何意义
在几何上,我们用什么来表示实数
实数可以用数轴上的点来表示.
实数
数轴上的点
(形)
(数)
一一对应
想一想?
x
0
1
实数的几何模型:
复数的一般形式
一个复数又该怎样表示呢?
回忆…
实部
虚部
(a,b∈R)
1.类比实数的几何意义思考复数的几何意义.
2.明确复数的两种几何意义.
3.了解复数模的意义,和共轭复数的概念。
体会数学抽象及数学运算素养,培养数形结合的直观想象的能力。
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
复数z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
(数)
(形)
一一对应
一一对应
一一对应
探究点1 复数的几何表示
x
y
0
Z(a,b)
建立了平面直角坐标系来表示复数的平面——复平面
x轴——实轴
y轴——虚轴
a
b
z=a+bi
这是复数的一种几何意义.
A.在复平面内,对应于实数的点都在实轴上
B.在复平面内,对应于纯虚数的点都在虚轴上
C.在复平面内,实轴上的点所对应的复数都是实数
D.在复平面内,虚轴上的点所对应的复数都是纯虚数
下列命题中的假命题是( )
D
【即时训练】
【解题关键】虚轴上的点除原点外都表示纯虚数。
实数绝对值的几何意义:
复数的模其实是实数绝对值概念的推广
x
O
A
a
|a| = |OA|
实数a在数轴上所对应的点A到原点O的距离.
x
O
z=a+bi
y
|z|=|OZ|
复数的模
复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离.
的几何意义:
Z(a,b)
注意 a+bi 与 a-bi 两复数的特点.
定义:实部相等,虚部互为相反数的两个复数叫做互为共轭复数.
复数 z=a+bi 的共轭复数记作
x
O
z=a+bi
y
Z(a,-b)
Z(a,b)
z=a-bi
在复平面内表示两个共轭复数的点,
关于实轴对称,并且他们的模相等
【即时训练】
【变式训练】
【变式1】已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围.
表示复数的点所在象限的问题
复数的实部与虚部所满足的不等式组的问题
转化
(几何问题)
(代数问题)
一种重要的数学思想:数形结合思想
复数的
几何意义
方法总结
核心知识
易错提醒
核心素养
(1)已知复平面内对应的点满足的条件求参数取值范围时,可根据
复数与点的对应关系,通过解方程(组)或不等式(组)求解.
(2)根据|a+bi|= 可把复数模的问题转化为实数问题解决.
(3)根据|z|=| |,可把复数模的问题转化为向量模的问题解决.
1.原点确定的复数是实数0,除了原点外,虚轴上的点都表示纯虚数.
2.复数的模是非负实数,因此复数的模可以比较大小.
1.数学抽象:复平面及复数的几何意义的理解.
2.逻辑推理:根据平面与向量的关系推出复数与向量的一一对应及复数模公式.
3.数学运算:根据复数与复平面的点一一对应求参数和求复数的模.
4.数学建模:根据复数的代数形式,数形结合,多方位了解复数的几何意义.
1. 复平面.
2. 复数与点的对应.
3. 复数与向量的对应.
4. 复数的模.
1.“a=0”是“复数a+bi (a , b∈R)所对应的点
在虚轴上”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.不充分不必要条件
C
D
3. 在复平面内,描出下列各复数的点:
x
y
O
⑴ 2+5i;
⑵ -3+2i;
⑶ 2-4i;
⑷-3-i;
⑸ 5;
⑹ -3i.
x
y
O
⑵
⑷
⑶
⑸
⑴
⑹
解析:
⑴ 2+5i;
⑵ -3+2i;
⑶ 2-4i;
⑷-3-i;
⑸ 5;
⑹ -3i.
解
析
:
因为
z
为纯虚数,
所以
设
z
=
a
i
(
a
∈
R
且
a
≠
0)
,又
|
-
1
+
i
|
=
2
,由
|
z
-
1|
=
|
-
1
+
i
|
,
得
a
2
+
1
=
2
,解得
a
=
±
1
,
所以
z
=
±
i.
自己活着,就是为了使别人活得更美好。
