1.5.1弹性碰撞和非弹性碰撞(共21张ppt)
文档属性
| 名称 | 1.5.1弹性碰撞和非弹性碰撞(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-06 12:07:44 | ||
图片预览





文档简介
(共21张PPT)
第一章 动量守恒定律
1.5.1 弹性碰撞和非弹性碰撞
物体在碰撞中的动量,变中有不变。那么,在碰撞中的能量如何?
新课引入
网球受球拍撞击却能够全身而退,只改变运动的方向
碰撞是自然界常见的现象。高速飞行的陨石撞击地球后对地表产生极大的破坏,最后终归静止;
掘进机和石块相遇,遇强则强,将石块击得粉碎······
碰撞:指的是两个物体在极短时间内发生相互作用,由于相互碰撞的物体组成的系统,外力远小于内力,可以忽略不计,系统在碰撞过程中动量守恒
碰撞及特点:
⑴作用时间极短(Δt→0);
⑵相互作用力先急剧增大,
后急剧减小,平均作用力很大;
⑷系统动量:系统总动量守恒
能量特点如何呢?
⑶位移:碰撞时间极短,:
①直接参与碰撞物体位移极小,有必要时可认为位置不变,。
②不直接参与碰撞的物体,位置不变,位移为零且运动状态不变。
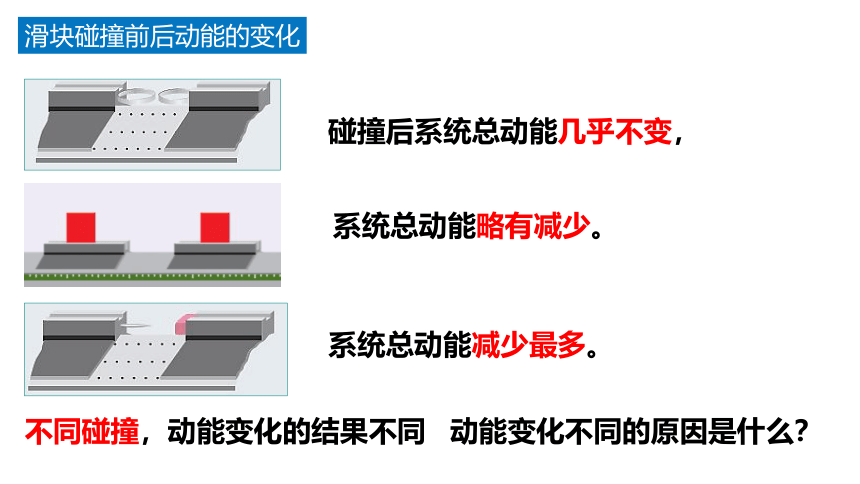
系统总动能减少最多。
滑块碰撞前后动能的变化
不同碰撞,动能变化的结果不同
动能变化不同的原因是什么?
碰撞后系统总动能几乎不变,
系统总动能略有减少。
一、 按碰撞前后速度方向分类
1.一维碰撞:
2.二维碰撞:
碰撞之前球的速度方向与两球心连线在同一条直线上,碰撞之后两球的速度方向仍会沿着这条直线。也称作正碰或对心碰撞
碰撞之前球的速度方向与两球心连线不在同一条直线上,碰撞之后两球的速度方向也不会沿着这条直线。也称作斜碰或非对心碰撞
碰撞的分类
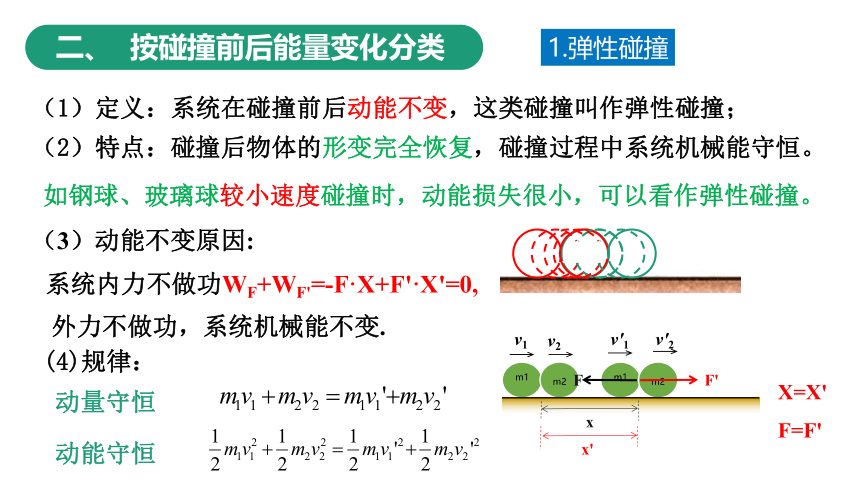
(1)定义:系统在碰撞前后动能不变,这类碰撞叫作弹性碰撞;
(2)特点:碰撞后物体的形变完全恢复,碰撞过程中系统机械能守恒。
1.弹性碰撞
如钢球、玻璃球较小速度碰撞时,动能损失很小,可以看作弹性碰撞。
二、 按碰撞前后能量变化分类
(3)动能不变原因:
x'
(4)规律:
动量守恒
动能守恒
系统内力不做功WF+WF'=-F·X+F'·X'=0,
外力不做功,系统机械能不变.
m1
m2
v'1
v'2
F'
X=X'
F=F'
v1
m1
m2
v2
x
F
(1)定义:系统在碰撞后动能减少,这类碰撞叫作非弹性碰撞;
(2)特点:碰撞后物体的不能完全恢复形变,碰撞过程中系统机械能减少;
2.非弹性碰撞
例如木制品的碰撞
(3)动能减少原因:
系统内力做负功WF+WF'=-F·X+F'·X'<0,
外力不做功,系统机械能减少.
(4)规律:
动量守恒
动能有损失
x'
m1
m2
v'1
F
F'
X>X'
F=F'
v1
m1
m2
v2
v'2
x
Δx
ΔX=X-X'较小
m1
m2
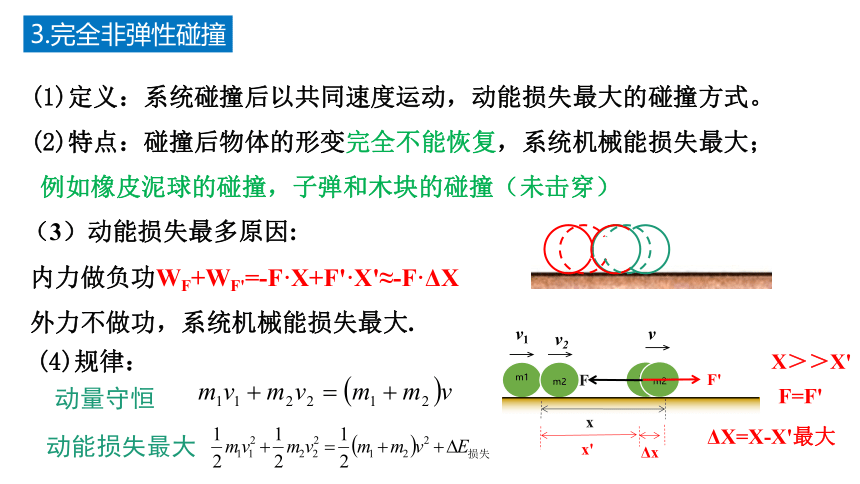
3.完全非弹性碰撞
(1)定义:系统碰撞后以共同速度运动,动能损失最大的碰撞方式。
(2)特点:碰撞后物体的形变完全不能恢复,系统机械能损失最大;
例如橡皮泥球的碰撞,子弹和木块的碰撞(未击穿)
(3)动能损失最多原因:
内力做负功WF+WF'=-F·X+F'·X'≈-F·ΔX
外力不做功,系统机械能损失最大.
动量守恒
动能损失最大
(4)规律:
x'
v
F'
ΔX=X-X'最大
F=F'
v1
m1
m2
v2
x
Δx
X>>X'
F
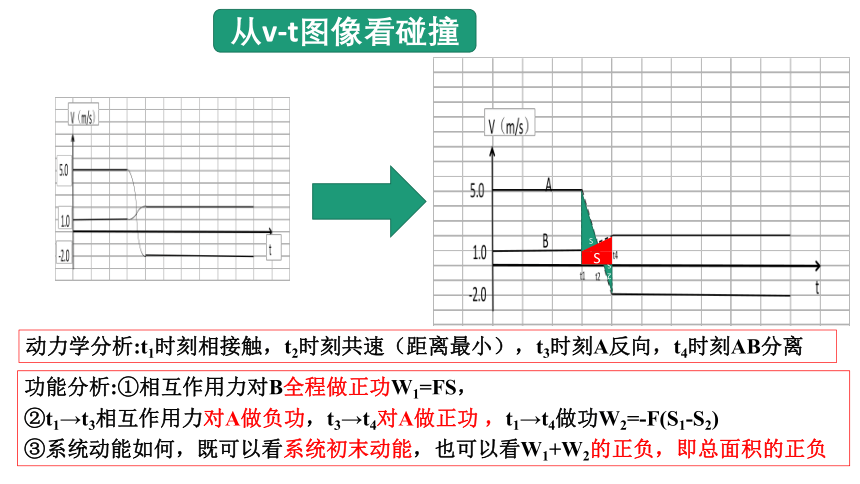
从v-t图像看碰撞
功能分析:①相互作用力对B全程做正功W1=FS,
②t1→t3相互作用力对A做负功,t3→t4对A做正功 ,t1→t4做功W2=-F(S1-S2)
③系统动能如何,既可以看系统初末动能,也可以看W1+W2的正负,即总面积的正负
动力学分析:t1时刻相接触,t2时刻共速(距离最小),t3时刻A反向,t4时刻AB分离
S1
2S
S
动量守恒
动能守恒
整理得
解得
弹性碰撞的一般规律
解得
碰撞结果不难记
两项相加是规律;
一 二 一,二 二 二;
分母都是1+2;
要问v‘2 是多少;
角标互换就可以;
1换2,2换1
两球速度交换
m1速度不变,m2以m1碰前速度的两倍向前运动
m1被按原来速率弹回,m2几乎末动。
1.m1=m2
2.m1>>m2
3.m1<4.m1>m2
5.m1<m2
弹性碰撞的特殊规律
若v2=0
两球都向前运动.
质量小的m1被反弹回去.
v1′=0,v2 ′=v1
v1′≈v1,v2 ′≈2v1
v1′≈-v1,v2 ′≈0
v1′>0,v2 ′>0
v1 ′<0,v2 ′>0
v1′<v1
(内力对m1做负功)
【例题1】速度为10m/s的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的4倍,碰撞是弹性的,求碰撞后两个小球的速度.
解:由于是弹性碰撞,根据动量守恒和动能守恒得
塑料球:
钢球:
与塑料球初速度方向相反
与塑料球初速度方向相同
【例题2】一 种未知粒子跟静止的氢原子核正碰,测出碰撞后氢原子核的速度3.3×107m/s.该未知粒子跟静止的氮原子核正碰时,测出碰撞后氮原子核的速度是4.4×106m/s.已知氢原子核的质量是mH,氮原子核的质量是14mH,上述碰撞都是弹性碰撞,求未知粒子的质量.
【查德威克发现中子实验】
碰后氮原子核的速度为:
解:设未知粒子质量m,速度v,它与氢和氮原子核碰撞都是弹性碰撞,
碰后氢原子核的速度为:
两式联立,解得未知粒子的质量为mH
3.速度要合理(符合物理情景)
物理情景:碰撞只发生一次.前后位置关系不变,速度变化
①碰前同向运动,碰前有:v后>v前,若碰后未反向,碰后有:v前≥v后
②碰前相向运动,碰后至少一个物体方向改变。
v2′
碰撞三原则
等价于: m1v12+m2v22 ≥ m1v1′2+m2v2′2
也等价于:P12/m1+p22/m2 ≥ P1 ′2/m1+p2′2/m2
1.系统动量守恒:碰撞前后系统的总动量守恒,.
2.动能不增加:碰撞后系统的总动能小于或等于碰撞前系统的总动能
【例题1】 质量相等的A、B两球在光滑水平桌面上沿同一直线、同一方向运动,A球的动量是7kg·m/s,B球的动量是5kg'm/s,A 球追上B球发生碰撞,碰撞后两球的动量可能值是( )
A.P'A=6 kg"m/s , p'B=6 kg'm/s B.P'A=3 kg:m/s , p'B=9kg'm/s
C.P'A=6.8kg·m/s , p'B=6.2kg·m/s D.P'A=-2kg·m/s , p'B=10kg·m/s
动量可能性判断的优先顺序
先动量守恒
再速度合理:碰后仍同向,则V后≤V前;碰前相向,必有反
最后动能不增加
A
【变式训练】两球A、B在光滑水平面上沿同一直线、同一方向运动, mA=1 kg, mB=2 kg, vA=6 m/s, vB=2 m/s。当A追上B并发生碰撞后,两球A、B速度的可能值是( )。
A.vA'=5 m/s,vB'=2.5 m/s B.vA'=2 m/s,vB'=4 m/s
C.vA'=-4 m/s,vB'=7 m/s D.vA'= 3m/s,vB'=3.5 m/s
BD
速度可能性判断的优先顺序
先速度合理:碰后仍同向,则V后≤V前;碰前相向,必有反
后动量守恒
最后动能不增加
【例题2】用轻弹簧相连的质量均为2kg的A、B两物块都以 v0=6m/s 的速度在光滑的水平地面上运动,弹簧处于原长,质量为4kg的物体C静止在前方,B与C碰撞后二者粘在一起运动,在此后的运动过程中,
试判断A的速度有可能向左吗?为什么?
解:以V0方向为正方向,
设某时刻A速度方向向左,大小为V1,此时BC速度为V2
对A、B、C系统:据动量守恒有:
(mA+mB)V0=-mAV1+(mB+mC)V2
则(mA+mB)V0<(mB+mC)V2
即V2>4m/s ---①
B、C碰后系统机械能为E= mAV02+(mB+mC)V共2 ---②
B、C碰后共速有:mBV0=(mB+mC)V共 ---③
解②③得E=48J,
据①可知BC动能Ek>48J
据机械能不增加原则可知
A的速度不可能向左。
【通过动量守恒将速度方向问题转化为速度大小问题求解是关键】
1.光滑水平面上,动能为E0 ,动量大小为p0 的小钢球1与静止的小钢球2发生弹性碰撞,碰后球1的运动反向,碰后球1的动能和动量大小分别记为 E1、p1,球2的动能和动量大小分别记为E2、p2,则必有 ( )
A. E1 < E0 B. p1 < p0
C. E2 > E0 D. p2 > p0
ABD
课堂练习
v0
1
2
2.如图甲所示,在光滑水平面上的两小球发生正碰。小球的质量分别为m1和m2。图乙为它们碰撞前后的s-t(位移一时间)图象。已知 m1=0.1 kg。由此可以判断( )
A. 碰前 m2 静止,m1 向右运动
B. 碰后 m2 和 m1 都向右运动
C. m2 = 0.3 kg
D. 碰撞过程中系统损失了 0.4 J 的机械能
AC
3.质量为m速度为v的A球,跟质量为3m的静止B球发生正碰,碰撞可能是弹性,也可能非弹性,碰后B球的速度可能为( )
A 0.6v B 0.4v C 0.2v D0.1v
B球速度的最小值发生在完全非弹性碰撞情形(内力做正功最少)
B球速度的最大值发生在弹性碰撞时:(内力做正功最多)
B
谢谢!
第一章 动量守恒定律
1.5.1 弹性碰撞和非弹性碰撞
物体在碰撞中的动量,变中有不变。那么,在碰撞中的能量如何?
新课引入
网球受球拍撞击却能够全身而退,只改变运动的方向
碰撞是自然界常见的现象。高速飞行的陨石撞击地球后对地表产生极大的破坏,最后终归静止;
掘进机和石块相遇,遇强则强,将石块击得粉碎······
碰撞:指的是两个物体在极短时间内发生相互作用,由于相互碰撞的物体组成的系统,外力远小于内力,可以忽略不计,系统在碰撞过程中动量守恒
碰撞及特点:
⑴作用时间极短(Δt→0);
⑵相互作用力先急剧增大,
后急剧减小,平均作用力很大;
⑷系统动量:系统总动量守恒
能量特点如何呢?
⑶位移:碰撞时间极短,:
①直接参与碰撞物体位移极小,有必要时可认为位置不变,。
②不直接参与碰撞的物体,位置不变,位移为零且运动状态不变。
系统总动能减少最多。
滑块碰撞前后动能的变化
不同碰撞,动能变化的结果不同
动能变化不同的原因是什么?
碰撞后系统总动能几乎不变,
系统总动能略有减少。
一、 按碰撞前后速度方向分类
1.一维碰撞:
2.二维碰撞:
碰撞之前球的速度方向与两球心连线在同一条直线上,碰撞之后两球的速度方向仍会沿着这条直线。也称作正碰或对心碰撞
碰撞之前球的速度方向与两球心连线不在同一条直线上,碰撞之后两球的速度方向也不会沿着这条直线。也称作斜碰或非对心碰撞
碰撞的分类
(1)定义:系统在碰撞前后动能不变,这类碰撞叫作弹性碰撞;
(2)特点:碰撞后物体的形变完全恢复,碰撞过程中系统机械能守恒。
1.弹性碰撞
如钢球、玻璃球较小速度碰撞时,动能损失很小,可以看作弹性碰撞。
二、 按碰撞前后能量变化分类
(3)动能不变原因:
x'
(4)规律:
动量守恒
动能守恒
系统内力不做功WF+WF'=-F·X+F'·X'=0,
外力不做功,系统机械能不变.
m1
m2
v'1
v'2
F'
X=X'
F=F'
v1
m1
m2
v2
x
F
(1)定义:系统在碰撞后动能减少,这类碰撞叫作非弹性碰撞;
(2)特点:碰撞后物体的不能完全恢复形变,碰撞过程中系统机械能减少;
2.非弹性碰撞
例如木制品的碰撞
(3)动能减少原因:
系统内力做负功WF+WF'=-F·X+F'·X'<0,
外力不做功,系统机械能减少.
(4)规律:
动量守恒
动能有损失
x'
m1
m2
v'1
F
F'
X>X'
F=F'
v1
m1
m2
v2
v'2
x
Δx
ΔX=X-X'较小
m1
m2
3.完全非弹性碰撞
(1)定义:系统碰撞后以共同速度运动,动能损失最大的碰撞方式。
(2)特点:碰撞后物体的形变完全不能恢复,系统机械能损失最大;
例如橡皮泥球的碰撞,子弹和木块的碰撞(未击穿)
(3)动能损失最多原因:
内力做负功WF+WF'=-F·X+F'·X'≈-F·ΔX
外力不做功,系统机械能损失最大.
动量守恒
动能损失最大
(4)规律:
x'
v
F'
ΔX=X-X'最大
F=F'
v1
m1
m2
v2
x
Δx
X>>X'
F
从v-t图像看碰撞
功能分析:①相互作用力对B全程做正功W1=FS,
②t1→t3相互作用力对A做负功,t3→t4对A做正功 ,t1→t4做功W2=-F(S1-S2)
③系统动能如何,既可以看系统初末动能,也可以看W1+W2的正负,即总面积的正负
动力学分析:t1时刻相接触,t2时刻共速(距离最小),t3时刻A反向,t4时刻AB分离
S1
2S
S
动量守恒
动能守恒
整理得
解得
弹性碰撞的一般规律
解得
碰撞结果不难记
两项相加是规律;
一 二 一,二 二 二;
分母都是1+2;
要问v‘2 是多少;
角标互换就可以;
1换2,2换1
两球速度交换
m1速度不变,m2以m1碰前速度的两倍向前运动
m1被按原来速率弹回,m2几乎末动。
1.m1=m2
2.m1>>m2
3.m1<
5.m1<m2
弹性碰撞的特殊规律
若v2=0
两球都向前运动.
质量小的m1被反弹回去.
v1′=0,v2 ′=v1
v1′≈v1,v2 ′≈2v1
v1′≈-v1,v2 ′≈0
v1′>0,v2 ′>0
v1 ′<0,v2 ′>0
v1′<v1
(内力对m1做负功)
【例题1】速度为10m/s的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的4倍,碰撞是弹性的,求碰撞后两个小球的速度.
解:由于是弹性碰撞,根据动量守恒和动能守恒得
塑料球:
钢球:
与塑料球初速度方向相反
与塑料球初速度方向相同
【例题2】一 种未知粒子跟静止的氢原子核正碰,测出碰撞后氢原子核的速度3.3×107m/s.该未知粒子跟静止的氮原子核正碰时,测出碰撞后氮原子核的速度是4.4×106m/s.已知氢原子核的质量是mH,氮原子核的质量是14mH,上述碰撞都是弹性碰撞,求未知粒子的质量.
【查德威克发现中子实验】
碰后氮原子核的速度为:
解:设未知粒子质量m,速度v,它与氢和氮原子核碰撞都是弹性碰撞,
碰后氢原子核的速度为:
两式联立,解得未知粒子的质量为mH
3.速度要合理(符合物理情景)
物理情景:碰撞只发生一次.前后位置关系不变,速度变化
①碰前同向运动,碰前有:v后>v前,若碰后未反向,碰后有:v前≥v后
②碰前相向运动,碰后至少一个物体方向改变。
v2′
碰撞三原则
等价于: m1v12+m2v22 ≥ m1v1′2+m2v2′2
也等价于:P12/m1+p22/m2 ≥ P1 ′2/m1+p2′2/m2
1.系统动量守恒:碰撞前后系统的总动量守恒,.
2.动能不增加:碰撞后系统的总动能小于或等于碰撞前系统的总动能
【例题1】 质量相等的A、B两球在光滑水平桌面上沿同一直线、同一方向运动,A球的动量是7kg·m/s,B球的动量是5kg'm/s,A 球追上B球发生碰撞,碰撞后两球的动量可能值是( )
A.P'A=6 kg"m/s , p'B=6 kg'm/s B.P'A=3 kg:m/s , p'B=9kg'm/s
C.P'A=6.8kg·m/s , p'B=6.2kg·m/s D.P'A=-2kg·m/s , p'B=10kg·m/s
动量可能性判断的优先顺序
先动量守恒
再速度合理:碰后仍同向,则V后≤V前;碰前相向,必有反
最后动能不增加
A
【变式训练】两球A、B在光滑水平面上沿同一直线、同一方向运动, mA=1 kg, mB=2 kg, vA=6 m/s, vB=2 m/s。当A追上B并发生碰撞后,两球A、B速度的可能值是( )。
A.vA'=5 m/s,vB'=2.5 m/s B.vA'=2 m/s,vB'=4 m/s
C.vA'=-4 m/s,vB'=7 m/s D.vA'= 3m/s,vB'=3.5 m/s
BD
速度可能性判断的优先顺序
先速度合理:碰后仍同向,则V后≤V前;碰前相向,必有反
后动量守恒
最后动能不增加
【例题2】用轻弹簧相连的质量均为2kg的A、B两物块都以 v0=6m/s 的速度在光滑的水平地面上运动,弹簧处于原长,质量为4kg的物体C静止在前方,B与C碰撞后二者粘在一起运动,在此后的运动过程中,
试判断A的速度有可能向左吗?为什么?
解:以V0方向为正方向,
设某时刻A速度方向向左,大小为V1,此时BC速度为V2
对A、B、C系统:据动量守恒有:
(mA+mB)V0=-mAV1+(mB+mC)V2
则(mA+mB)V0<(mB+mC)V2
即V2>4m/s ---①
B、C碰后系统机械能为E= mAV02+(mB+mC)V共2 ---②
B、C碰后共速有:mBV0=(mB+mC)V共 ---③
解②③得E=48J,
据①可知BC动能Ek>48J
据机械能不增加原则可知
A的速度不可能向左。
【通过动量守恒将速度方向问题转化为速度大小问题求解是关键】
1.光滑水平面上,动能为E0 ,动量大小为p0 的小钢球1与静止的小钢球2发生弹性碰撞,碰后球1的运动反向,碰后球1的动能和动量大小分别记为 E1、p1,球2的动能和动量大小分别记为E2、p2,则必有 ( )
A. E1 < E0 B. p1 < p0
C. E2 > E0 D. p2 > p0
ABD
课堂练习
v0
1
2
2.如图甲所示,在光滑水平面上的两小球发生正碰。小球的质量分别为m1和m2。图乙为它们碰撞前后的s-t(位移一时间)图象。已知 m1=0.1 kg。由此可以判断( )
A. 碰前 m2 静止,m1 向右运动
B. 碰后 m2 和 m1 都向右运动
C. m2 = 0.3 kg
D. 碰撞过程中系统损失了 0.4 J 的机械能
AC
3.质量为m速度为v的A球,跟质量为3m的静止B球发生正碰,碰撞可能是弹性,也可能非弹性,碰后B球的速度可能为( )
A 0.6v B 0.4v C 0.2v D0.1v
B球速度的最小值发生在完全非弹性碰撞情形(内力做正功最少)
B球速度的最大值发生在弹性碰撞时:(内力做正功最多)
B
谢谢!
