人教版七年级下册5.3.2命题、定理、证明课件(共18张PPT)
文档属性
| 名称 | 人教版七年级下册5.3.2命题、定理、证明课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 299.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 08:32:50 | ||
图片预览






文档简介
(共18张PPT)
5.3.2命题、定理、证明
(第二课时)
第五章相交线与平行线 5.3平行线的性质
(1)两点确定一条直线.
(2)经过直线外一点有且只有一条直线与这条直线平行;
(3)如果两个角互补,那么它们是邻补角;
(4)对顶角相等
(5)内错角相等,两直线平行。
1.创设情境,引出新课。
问题1 (多媒体展示)判断下列命题是真命题还是假命题?
真命题
真命题
真命题
真命题
假命题
一些命题的正确性是经过推理证实的,这样得到的真命题叫做定理.
定理的概念
你学过那些定理?
内错角相等,两直线平行。
同旁内角互补,两直线平行。
1 、 平行线的判定定理:
2、平行线的性质定理:
两直线平行,内错角相等。
两直线平行,同旁内角互补。
定理的作用----- 定理可以作为推理的依据.
一个命题的正确性需要经过推理,才能作出判断,这个推理的过程叫做证明。
证明的概念
已知:如图,AB 和CD相交于点O,∠A=∠B.
求证:∠C=∠D.
证明:∵∠A=∠B(已知),
∴AC∥BD ( ).
∴∠C=∠D ( ).
内错角相等,两直线平行
两直线平行,内错角相等
1.在下面的括号内,填上推理的依据.
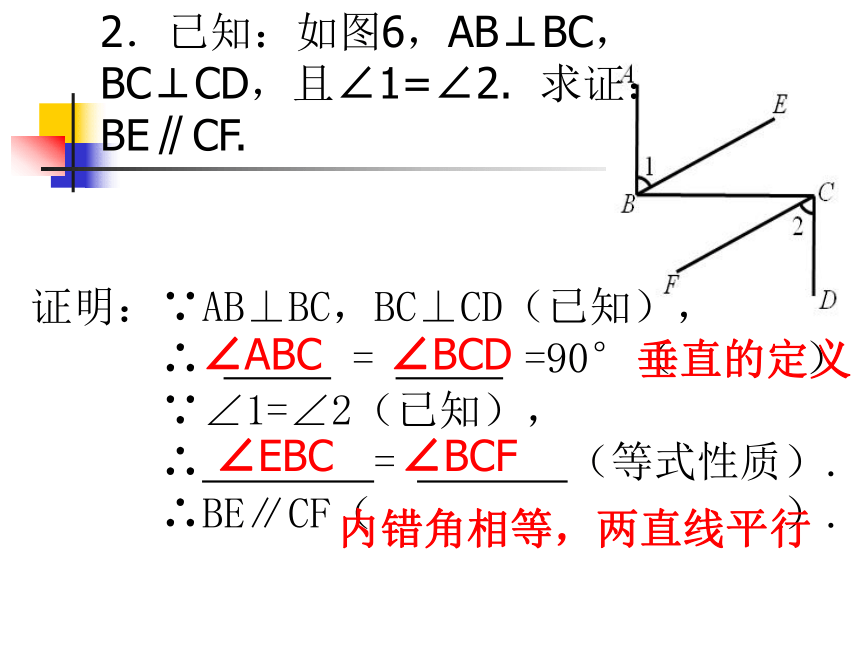
证明:∵AB⊥BC,BC⊥CD(已知),
∴ = =90°( )
∵∠1=∠2(已知),
∴ = (等式性质).
∴BE∥CF( ).
2.已知:如图6,AB⊥BC,BC⊥CD,且∠1=∠2. 求证:BE∥CF.
内错角相等,两直线平行
∠ABC ∠BCD
垂直的定义
∠EBC ∠BCF
问题2 判断下面两个命题是真命题还是假命题,并思考如何证明命题的真假?
命题1:在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
命题2:相等的角是对顶角.
2.协作探究,掌握新知
真命题
假命题
命题1:在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
已知:如图2 ,AD∥BC,∠A=∠C
求证:AB∥CD。
3.动手操作,深化理解。
方法一:
证明:∵AD∥BC(已知)
∴∠A=∠CBE(两直线平行,同位角相等)
∵∠A=∠C(已知)
∴∠C=∠CBE(等量代换)
∴AB∥CD(内错角相等,两直线平行)
4.分析实验,辨析说理。
命题2:
相等的角是对顶角
假命题
举反例
举反例
答:此命题为假命题,
反例:如图OC是∠ AOB的角平分线
∠1=∠2,但∠1和∠2就不是对顶角。
2.命题“同位角相等”是真命题吗?如果是,说出理由;如果不是,请举出反例.
当堂训练
原命题是假命题,
反例:
如图,∠1与∠2是同位角,
∠1>∠2,它们不相等.
答:
5.归纳小结,知识梳理
(1)定理:经过推理证实的真命题
(2)证明:推理的过程
注意:证明过程中每一步推理要
有理有据。
相交线
平行线
邻补角
对顶角
垂线
判定
性质
命题
真命题
假命题
证明
举反例
第五章相交线与平行线
三线八角
三线八角
三线八角
5.布置作业
教科书P23页12、13
目标检测
1.在下面的括号内,填上推理的依据.
如图,AB ∥ CD,CB ∥ DE ,
求证∠ B+ ∠D=1800
证明:
∵ AB ∥ CD,
∴ ∠B= ∠C( )
∵ CB ∥ DE
∴ ∠ C+ ∠ D=1800( )
∴ ∠ B+ ∠ D=1800( )
等量代换
两直线平行,内错角相等
两直线平行,同旁内角互补
2.命题“同旁内角互补”是真命题吗?如果是,说出理由;如果不是,请举出反例.
目标检测
原命题是假命题,
反例:
如图,∠1与∠2是同旁内角,
∠1+∠2<1800,它们不互补.
答:
答:
5.3.2命题、定理、证明
(第二课时)
第五章相交线与平行线 5.3平行线的性质
(1)两点确定一条直线.
(2)经过直线外一点有且只有一条直线与这条直线平行;
(3)如果两个角互补,那么它们是邻补角;
(4)对顶角相等
(5)内错角相等,两直线平行。
1.创设情境,引出新课。
问题1 (多媒体展示)判断下列命题是真命题还是假命题?
真命题
真命题
真命题
真命题
假命题
一些命题的正确性是经过推理证实的,这样得到的真命题叫做定理.
定理的概念
你学过那些定理?
内错角相等,两直线平行。
同旁内角互补,两直线平行。
1 、 平行线的判定定理:
2、平行线的性质定理:
两直线平行,内错角相等。
两直线平行,同旁内角互补。
定理的作用----- 定理可以作为推理的依据.
一个命题的正确性需要经过推理,才能作出判断,这个推理的过程叫做证明。
证明的概念
已知:如图,AB 和CD相交于点O,∠A=∠B.
求证:∠C=∠D.
证明:∵∠A=∠B(已知),
∴AC∥BD ( ).
∴∠C=∠D ( ).
内错角相等,两直线平行
两直线平行,内错角相等
1.在下面的括号内,填上推理的依据.
证明:∵AB⊥BC,BC⊥CD(已知),
∴ = =90°( )
∵∠1=∠2(已知),
∴ = (等式性质).
∴BE∥CF( ).
2.已知:如图6,AB⊥BC,BC⊥CD,且∠1=∠2. 求证:BE∥CF.
内错角相等,两直线平行
∠ABC ∠BCD
垂直的定义
∠EBC ∠BCF
问题2 判断下面两个命题是真命题还是假命题,并思考如何证明命题的真假?
命题1:在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
命题2:相等的角是对顶角.
2.协作探究,掌握新知
真命题
假命题
命题1:在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
已知:如图2 ,AD∥BC,∠A=∠C
求证:AB∥CD。
3.动手操作,深化理解。
方法一:
证明:∵AD∥BC(已知)
∴∠A=∠CBE(两直线平行,同位角相等)
∵∠A=∠C(已知)
∴∠C=∠CBE(等量代换)
∴AB∥CD(内错角相等,两直线平行)
4.分析实验,辨析说理。
命题2:
相等的角是对顶角
假命题
举反例
举反例
答:此命题为假命题,
反例:如图OC是∠ AOB的角平分线
∠1=∠2,但∠1和∠2就不是对顶角。
2.命题“同位角相等”是真命题吗?如果是,说出理由;如果不是,请举出反例.
当堂训练
原命题是假命题,
反例:
如图,∠1与∠2是同位角,
∠1>∠2,它们不相等.
答:
5.归纳小结,知识梳理
(1)定理:经过推理证实的真命题
(2)证明:推理的过程
注意:证明过程中每一步推理要
有理有据。
相交线
平行线
邻补角
对顶角
垂线
判定
性质
命题
真命题
假命题
证明
举反例
第五章相交线与平行线
三线八角
三线八角
三线八角
5.布置作业
教科书P23页12、13
目标检测
1.在下面的括号内,填上推理的依据.
如图,AB ∥ CD,CB ∥ DE ,
求证∠ B+ ∠D=1800
证明:
∵ AB ∥ CD,
∴ ∠B= ∠C( )
∵ CB ∥ DE
∴ ∠ C+ ∠ D=1800( )
∴ ∠ B+ ∠ D=1800( )
等量代换
两直线平行,内错角相等
两直线平行,同旁内角互补
2.命题“同旁内角互补”是真命题吗?如果是,说出理由;如果不是,请举出反例.
目标检测
原命题是假命题,
反例:
如图,∠1与∠2是同旁内角,
∠1+∠2<1800,它们不互补.
答:
答:
