甘肃省酒泉市实验中学2021-2022学年高一下学期数学期中考试试卷(Word版含解析)
文档属性
| 名称 | 甘肃省酒泉市实验中学2021-2022学年高一下学期数学期中考试试卷(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 545.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 00:00:00 | ||
图片预览




文档简介
酒泉市实验中学2021-2022学年度第二学期高一数学期中考试试卷及详细解析
考察范围:湘教版必修第一册第6章《统计学初步》、第二册第1章《平面向量及其应用》、
第2章《三角恒等变换》、第3章《复数》
试卷总分:150分 考试时间:120分钟
一、单选题(共45分)
1.(本题5分)为了解某中学2500名学生家长对“骑电动车需戴头盔”的态度,从中随机调查400名家长,结果有380名家长持赞成态度,则下列说法正确的是( )
A.调查方式是全面调查 B.该校只有380名家长持赞成态度
C.样本是400 D.该校约有95%的家长持赞成态度
2.(本题5分)若复数为纯虚数,则实数=( )
A.或2 B.或1 C. D.1
3.(本题5分)已知复数,为z的共轭复数,则的虚部为( )
A. B. C. D.
4.(本题5分)港珠澳大桥是中国境内一座连接中国香港、广东珠海和中国澳门的桥隧工程,因其超大的建筑规模、空前的施工难度以及顶尖的建造技术闻名世界,为内地前往香港的游客提供了便捷的交通途径,某旅行社分年龄统计了大桥落地以后,由香港大桥实现内地前往香港的老中青旅客的比例分别为,现使用分层抽样的方法从这些旅客中随机抽取名,若青年旅客抽到60人,则( )
A.老年旅客抽到150人
B.中年旅客抽到20人
C.
D.被抽到的老年旅客以及中年旅客人数之和超过200
5.(本题5分)设一组样本数据,,,的方差为0.01,则数据,,,的方差为( )
A.0.01 B.0.1 C.1 D.10
6.(本题5分)某学校于3月12日组织师生举行植树活动,购买垂柳、银杏、侧柏、海桐四种树苗共计1200棵,比例如图所示.高一、高二、高三报名参加植树活动的人数分别为600,400,200,若每种树苗均按各年级报名人数的比例进行分配,则高三年级应分得侧柏的数量为( )
A.34 B.46 C.50 D.70
7.(本题5分)下列说法中正确的是( )
A.向量的模都是正实数
B.单位向量都是相等向量
C.向量的大小与方向无关
D.方向不同的向量不能比较大小,但同向的向量可以比较大小
8.(本题5分)已知向量,若,则实数的值为( )
A.1 B.0 C. D.
9.(本题5分)如图所示,为测一树的高度,在地面上选取A,B两点,从A,B两点分别测得树尖的仰角为,,且A,B两点之间的距离为30,则该树的高度为( )
A. B.
C. D.
二、多选题(共15分)
10.(本题5分)关于平面向量,,,下列命题中错误的是( )
A.若,则存在,使得 B.若,则
C.若,则 D.
11.(本题5分)在中,角,,对应的边分别为,,,已知,,,则边长的值为( )
A. B. C. D.
12.(本题5分)下列等式成立的是( )
A. B.
C. D.
三、填空题(共20分)
13.(本题5分)已知向量,则___________.
14.(本题5分)已知,,则___________.
15.(本题5分)甲、乙两种冬小麦试验品种连续5年的平均单位面积产量如下(单位:)
品种 第1年 第2年 第3年 第4年 第5年
甲 9.8 9.9 10.1 10 10.2
乙 9.4 10.3 10.8 9.7 9.8
其中产量比较稳定的小麦品种是______________________;
16.(本题5分)已知,,,则在方向上的投影为___________.
四、解答题(共70分)
17.(本题10分)设两个非零向量与不共线.
(1)若,,,求证:,,三点共线;
(2)试确定实数,使和反向.
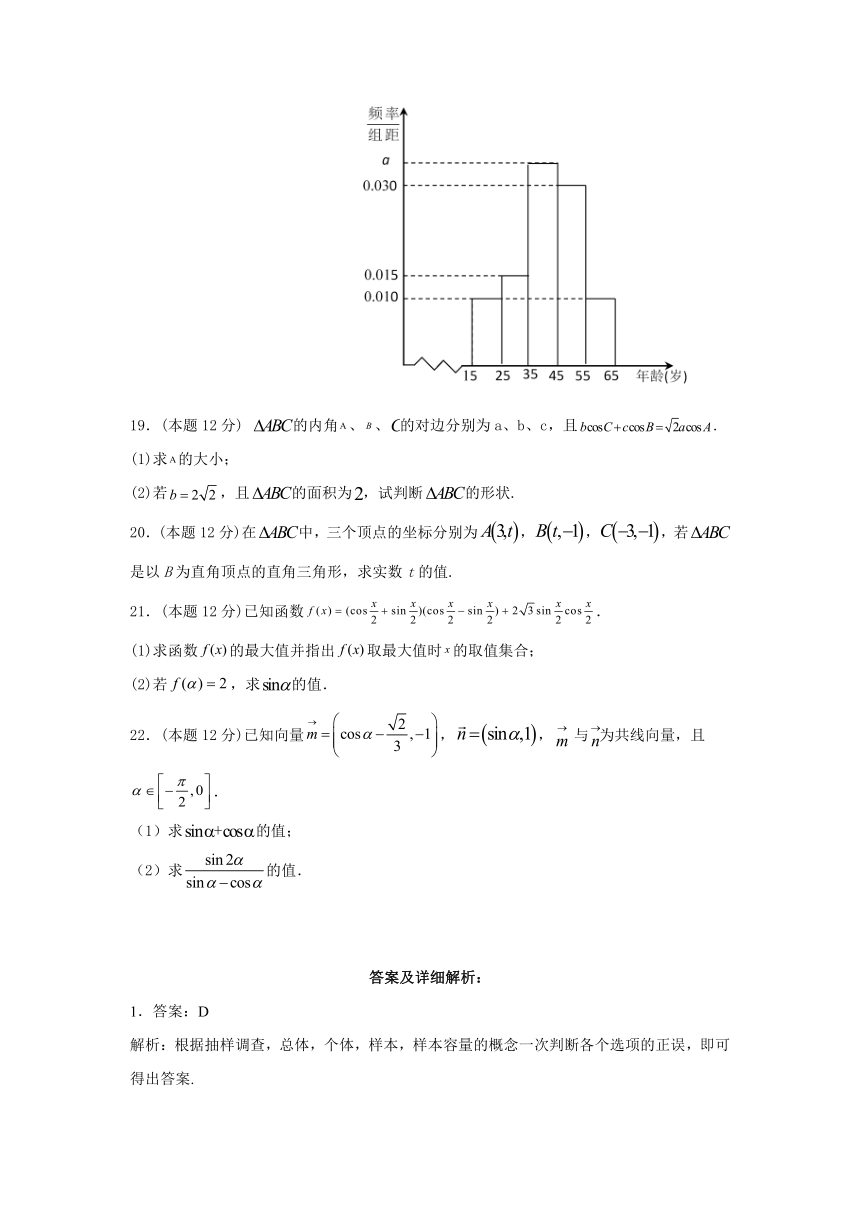
18.(本题12分)为激活国内消费市场,挽回疫情造成的损失,国家出台一系列的促进国内消费的优惠政策.某机构从某一电商的线上交易大数据中来跟踪调查消费者的购买力,现从电商平台消费人群中随机选出200人,并将这200人按年龄分组,记第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65),得到如下频率分布直方图:
(1)求出频率分布直方图中的a值和这200人的年龄的众数、中位数及平均数;
(2)求这200人的年龄的众数、中位数及平均数;
19.(本题12分) 的内角、、的对边分别为a、b、c,且.
(1)求的大小;
(2)若,且的面积为,试判断的形状.
20.(本题12分)在中,三个顶点的坐标分别为,,,若是以B为直角顶点的直角三角形,求实数t的值.
21.(本题12分)已知函数.
(1)求函数的最大值并指出取最大值时的取值集合;
(2)若,求的值.
22.(本题12分)已知向量,,与为共线向量,且.
(1)求的值;
(2)求的值.
答案及详细解析:
1.答案:D
解析:根据抽样调查,总体,个体,样本,样本容量的概念一次判断各个选项的正误,即可得出答案.
A:调查方式是抽样调查,不是全面调查,故A错;
B:400名家长里有380名家长持赞成态度,
按照比例推算,全校2500名学生家长中会有2375名家长持赞成态度,故B错;
C:样本是400名家长对“骑电动车需戴头盔”的态度,
样本容量是400,故C错;
D:该校约有:的家长持赞成态度,故D正确;
故选:D.
2.答案:C
解析:因为复数(为虚数单位)为纯虚数,
所以,
由,得或,
由,得且,
所以,
故选:C
3.答案:D
解析:因为,所以,
所以,
故其虚部为.
故选:D
4.答案:C
解析:由题意,香港大桥实现内地前往香港的老中青旅客的比例分别为,现使用分层抽样的方法从这些旅客中随机抽取名,若青年旅客抽到60人,
所以,解得人.
故选:C.
5.答案:C
解析:由题意数据,,,的方差为.
故选:C.
6.答案:C
解析:由扇形统计图知,购买的1200棵树苗中,侧柏的数量为,
依题意,高一、高二、高三分到的侧柏的棵数比为:,
所以高三年级应分得侧柏的数量为.
故选:C
7.答案:C
解析:零向量的模为0,故A不正确;
单位向量的方向可以是任意的,故B不正确;
向量的大小即为向量的模,指的是有向线段的长度,与方向无关,故C正确;
不管向量的方向如何,它们都不能比较大小,故D不正确.
故选:C
8.答案:A
解析:因为,
所以,.
因为,
所以,解得:.
故选:A
9.答案:D
解析:设树高为h,则,又,
所以,
故选:D
10.答案:CD
解析:由共线向量定理可知:A正确;
当,则,B正确;
若,且,则不一定成立,C错误;
对于非零向量,,,当与不共线,且,时:,D错误.
故选:CD.
11.答案:AB
解析:在中,,,,
由余弦定理得,
,
,
,
解得或,
故选:AB
12.答案:AC
解析:对于A选项,,A对;
对于B选项,,B错;
对于C选项,
,C对;
对于D选项,
,D错.
故选:AC.
13.答案:
解析:根据向量的运算法则,可得.
故答案为:.
14.答案:
解析:由,可得,
则由,可得,
故答案为:
15.答案:甲
解析:由题意知,,
;
,
.
.
所以产量比较稳定的小麦品种是甲,
故答案为:甲
16.答案:
解析:设,的夹角为,因为,
所以,
所以,故在方向上的投影为·
故答案为:
17.答案:(1)证明见解析;(2)
解析:(1)证明: ,
,且,
与共线,且与有公共点,
,,三点共线;
(2)设,,且不共线,
,解得或.
容易验证,时,和反向。
∴
18.答案:(1);(2) 众数40、中位数42.1,平均数41.5
解析:(1)依据频率分布直方图的性质去求a值和众数、中位数及平均数;
由题意得:,所以;
(2)众数为最高小矩形底边中点的横坐标,即40;
设中位数为x,则
平均数为:
则可以估计这200人的年龄的众数为40、中位数为及平均数为
19.答案:(1);(2)等腰直角三角形
解析:(1)由及正弦定理得,
得,
因为,则,所以,则.
(2)因为,所以.
由余弦定理得,得,
因为,且,所以为等腰直角三角形.
20.答案:t的值是3.
解析:由
又,即,
,解得或,
当时,点B与点C重合,不符合题意,
故t的值是3.
21.答案:(1)2,;(2)
解析:(1),
,,
,
当时,,
此时,所以
取最大值时的取值集合,
(2),即,,,
,,.
22.答案:(1);(2).
解析:(1)∵与为共线向量,
∴,
即.
(2)∵,∴.
∴.
又∵,∴.
∴.∴.
考察范围:湘教版必修第一册第6章《统计学初步》、第二册第1章《平面向量及其应用》、
第2章《三角恒等变换》、第3章《复数》
试卷总分:150分 考试时间:120分钟
一、单选题(共45分)
1.(本题5分)为了解某中学2500名学生家长对“骑电动车需戴头盔”的态度,从中随机调查400名家长,结果有380名家长持赞成态度,则下列说法正确的是( )
A.调查方式是全面调查 B.该校只有380名家长持赞成态度
C.样本是400 D.该校约有95%的家长持赞成态度
2.(本题5分)若复数为纯虚数,则实数=( )
A.或2 B.或1 C. D.1
3.(本题5分)已知复数,为z的共轭复数,则的虚部为( )
A. B. C. D.
4.(本题5分)港珠澳大桥是中国境内一座连接中国香港、广东珠海和中国澳门的桥隧工程,因其超大的建筑规模、空前的施工难度以及顶尖的建造技术闻名世界,为内地前往香港的游客提供了便捷的交通途径,某旅行社分年龄统计了大桥落地以后,由香港大桥实现内地前往香港的老中青旅客的比例分别为,现使用分层抽样的方法从这些旅客中随机抽取名,若青年旅客抽到60人,则( )
A.老年旅客抽到150人
B.中年旅客抽到20人
C.
D.被抽到的老年旅客以及中年旅客人数之和超过200
5.(本题5分)设一组样本数据,,,的方差为0.01,则数据,,,的方差为( )
A.0.01 B.0.1 C.1 D.10
6.(本题5分)某学校于3月12日组织师生举行植树活动,购买垂柳、银杏、侧柏、海桐四种树苗共计1200棵,比例如图所示.高一、高二、高三报名参加植树活动的人数分别为600,400,200,若每种树苗均按各年级报名人数的比例进行分配,则高三年级应分得侧柏的数量为( )
A.34 B.46 C.50 D.70
7.(本题5分)下列说法中正确的是( )
A.向量的模都是正实数
B.单位向量都是相等向量
C.向量的大小与方向无关
D.方向不同的向量不能比较大小,但同向的向量可以比较大小
8.(本题5分)已知向量,若,则实数的值为( )
A.1 B.0 C. D.
9.(本题5分)如图所示,为测一树的高度,在地面上选取A,B两点,从A,B两点分别测得树尖的仰角为,,且A,B两点之间的距离为30,则该树的高度为( )
A. B.
C. D.
二、多选题(共15分)
10.(本题5分)关于平面向量,,,下列命题中错误的是( )
A.若,则存在,使得 B.若,则
C.若,则 D.
11.(本题5分)在中,角,,对应的边分别为,,,已知,,,则边长的值为( )
A. B. C. D.
12.(本题5分)下列等式成立的是( )
A. B.
C. D.
三、填空题(共20分)
13.(本题5分)已知向量,则___________.
14.(本题5分)已知,,则___________.
15.(本题5分)甲、乙两种冬小麦试验品种连续5年的平均单位面积产量如下(单位:)
品种 第1年 第2年 第3年 第4年 第5年
甲 9.8 9.9 10.1 10 10.2
乙 9.4 10.3 10.8 9.7 9.8
其中产量比较稳定的小麦品种是______________________;
16.(本题5分)已知,,,则在方向上的投影为___________.
四、解答题(共70分)
17.(本题10分)设两个非零向量与不共线.
(1)若,,,求证:,,三点共线;
(2)试确定实数,使和反向.
18.(本题12分)为激活国内消费市场,挽回疫情造成的损失,国家出台一系列的促进国内消费的优惠政策.某机构从某一电商的线上交易大数据中来跟踪调查消费者的购买力,现从电商平台消费人群中随机选出200人,并将这200人按年龄分组,记第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65),得到如下频率分布直方图:
(1)求出频率分布直方图中的a值和这200人的年龄的众数、中位数及平均数;
(2)求这200人的年龄的众数、中位数及平均数;
19.(本题12分) 的内角、、的对边分别为a、b、c,且.
(1)求的大小;
(2)若,且的面积为,试判断的形状.
20.(本题12分)在中,三个顶点的坐标分别为,,,若是以B为直角顶点的直角三角形,求实数t的值.
21.(本题12分)已知函数.
(1)求函数的最大值并指出取最大值时的取值集合;
(2)若,求的值.
22.(本题12分)已知向量,,与为共线向量,且.
(1)求的值;
(2)求的值.
答案及详细解析:
1.答案:D
解析:根据抽样调查,总体,个体,样本,样本容量的概念一次判断各个选项的正误,即可得出答案.
A:调查方式是抽样调查,不是全面调查,故A错;
B:400名家长里有380名家长持赞成态度,
按照比例推算,全校2500名学生家长中会有2375名家长持赞成态度,故B错;
C:样本是400名家长对“骑电动车需戴头盔”的态度,
样本容量是400,故C错;
D:该校约有:的家长持赞成态度,故D正确;
故选:D.
2.答案:C
解析:因为复数(为虚数单位)为纯虚数,
所以,
由,得或,
由,得且,
所以,
故选:C
3.答案:D
解析:因为,所以,
所以,
故其虚部为.
故选:D
4.答案:C
解析:由题意,香港大桥实现内地前往香港的老中青旅客的比例分别为,现使用分层抽样的方法从这些旅客中随机抽取名,若青年旅客抽到60人,
所以,解得人.
故选:C.
5.答案:C
解析:由题意数据,,,的方差为.
故选:C.
6.答案:C
解析:由扇形统计图知,购买的1200棵树苗中,侧柏的数量为,
依题意,高一、高二、高三分到的侧柏的棵数比为:,
所以高三年级应分得侧柏的数量为.
故选:C
7.答案:C
解析:零向量的模为0,故A不正确;
单位向量的方向可以是任意的,故B不正确;
向量的大小即为向量的模,指的是有向线段的长度,与方向无关,故C正确;
不管向量的方向如何,它们都不能比较大小,故D不正确.
故选:C
8.答案:A
解析:因为,
所以,.
因为,
所以,解得:.
故选:A
9.答案:D
解析:设树高为h,则,又,
所以,
故选:D
10.答案:CD
解析:由共线向量定理可知:A正确;
当,则,B正确;
若,且,则不一定成立,C错误;
对于非零向量,,,当与不共线,且,时:,D错误.
故选:CD.
11.答案:AB
解析:在中,,,,
由余弦定理得,
,
,
,
解得或,
故选:AB
12.答案:AC
解析:对于A选项,,A对;
对于B选项,,B错;
对于C选项,
,C对;
对于D选项,
,D错.
故选:AC.
13.答案:
解析:根据向量的运算法则,可得.
故答案为:.
14.答案:
解析:由,可得,
则由,可得,
故答案为:
15.答案:甲
解析:由题意知,,
;
,
.
.
所以产量比较稳定的小麦品种是甲,
故答案为:甲
16.答案:
解析:设,的夹角为,因为,
所以,
所以,故在方向上的投影为·
故答案为:
17.答案:(1)证明见解析;(2)
解析:(1)证明: ,
,且,
与共线,且与有公共点,
,,三点共线;
(2)设,,且不共线,
,解得或.
容易验证,时,和反向。
∴
18.答案:(1);(2) 众数40、中位数42.1,平均数41.5
解析:(1)依据频率分布直方图的性质去求a值和众数、中位数及平均数;
由题意得:,所以;
(2)众数为最高小矩形底边中点的横坐标,即40;
设中位数为x,则
平均数为:
则可以估计这200人的年龄的众数为40、中位数为及平均数为
19.答案:(1);(2)等腰直角三角形
解析:(1)由及正弦定理得,
得,
因为,则,所以,则.
(2)因为,所以.
由余弦定理得,得,
因为,且,所以为等腰直角三角形.
20.答案:t的值是3.
解析:由
又,即,
,解得或,
当时,点B与点C重合,不符合题意,
故t的值是3.
21.答案:(1)2,;(2)
解析:(1),
,,
,
当时,,
此时,所以
取最大值时的取值集合,
(2),即,,,
,,.
22.答案:(1);(2).
解析:(1)∵与为共线向量,
∴,
即.
(2)∵,∴.
∴.
又∵,∴.
∴.∴.
同课章节目录
