16.3 分式方程复习课件
文档属性
| 名称 | 16.3 分式方程复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 347.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-25 18:11:50 | ||
图片预览








文档简介
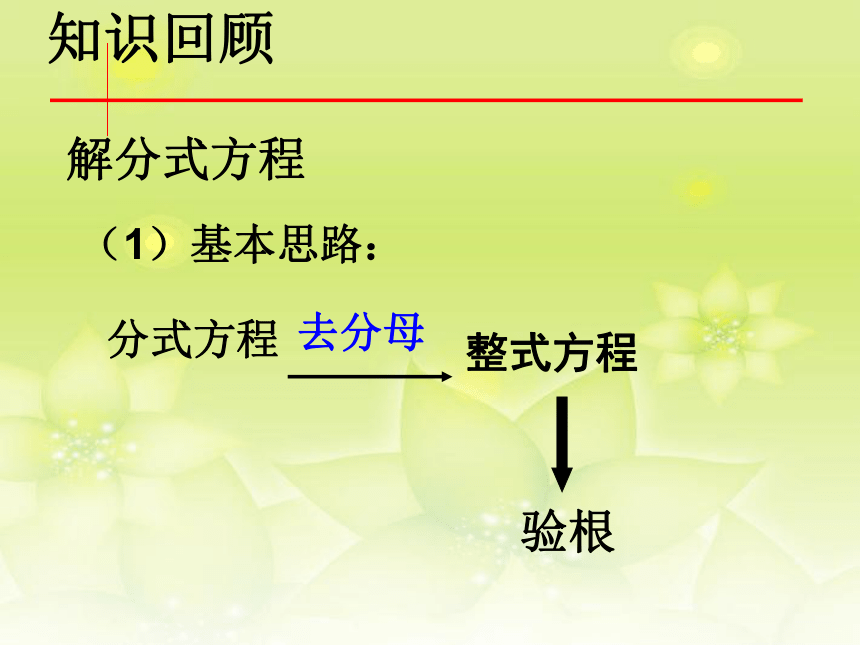
课件20张PPT。第十六章 分式方程复习课解分式方程分式方程去分母整式方程(1)基本思路:验根知识回顾(2).解分式方程的一般步骤 (1)、 在方程的两边都乘以最简公分母,约去分母,化成整式方程.
(2)、解这个整式方程.
(3)、 把整式方程的根代入最简公分母,看结果是不是为零,使最简公分母为零的根是原方程的增根,必须舍去.
(4)、写出原方程的根.增根产生的原因:分式方程两边同乘以一个 零因式后,所得的根是整式方程的根,而不是分式方程的根.
所以我们解分式方程时一定要代入最简公分母检验
解分式方程出现增根应舍去(3)解分式方程的最大特点: 根的检验方程两边都乘以解得检验:当x=3时,(x+3)(x-3)=0∴原方程无解得,(x+3)-8x=x2-9-x(x+3)∴ x=3是原方程的增根 解:原方程可化为:注意检验不要漏乘例2 .解关于x的方程:解:方程两边同乘以(x+1)(x-1),得
(a+b)(x-1)+(a-b)(x+1)=a2-b2
(a+b)x-a-b+(a-b)x+a-b= a2-b2
(a+b+a-b)x-2b= a2-b2
2ax= a2-b2+2b注意:方程两边同除以未知数系数时,必须讨论字母系数的取值情况a2-b2+2b 1.解方程2.解关于x的方程(1)一件工作甲单独做要m小时完成,乙单独做要n小时完成,如果两人合做,完成这
件工作的时间是______小时; (2)某食堂有米m公斤,原计划每天用粮a公斤,现在每天节约用粮b公斤,则可以
比原计划多用天数是______; 列分式方程解应用题解方程大显身手(1)(2)2.计算:(1) (-2)-3; 注:负整数次幂:任何不等于零的数的负整数次幂,等于这个数的正整数次幂的倒数。3、计算:分式方程解的情况 X=25X=1或x=-12或0变式3、当a为何值时,方程
的解是正数?变式4、当a为何值时,方程
无解?若解是负数呢?1.若方程 有增根,则增根应是 .
2.解关于x的方程
产生增根,则常数a= 。大显身手X=-2-4或63.当m为何值时,方程 解为非负数?再见
(2)、解这个整式方程.
(3)、 把整式方程的根代入最简公分母,看结果是不是为零,使最简公分母为零的根是原方程的增根,必须舍去.
(4)、写出原方程的根.增根产生的原因:分式方程两边同乘以一个 零因式后,所得的根是整式方程的根,而不是分式方程的根.
所以我们解分式方程时一定要代入最简公分母检验
解分式方程出现增根应舍去(3)解分式方程的最大特点: 根的检验方程两边都乘以解得检验:当x=3时,(x+3)(x-3)=0∴原方程无解得,(x+3)-8x=x2-9-x(x+3)∴ x=3是原方程的增根 解:原方程可化为:注意检验不要漏乘例2 .解关于x的方程:解:方程两边同乘以(x+1)(x-1),得
(a+b)(x-1)+(a-b)(x+1)=a2-b2
(a+b)x-a-b+(a-b)x+a-b= a2-b2
(a+b+a-b)x-2b= a2-b2
2ax= a2-b2+2b注意:方程两边同除以未知数系数时,必须讨论字母系数的取值情况a2-b2+2b 1.解方程2.解关于x的方程(1)一件工作甲单独做要m小时完成,乙单独做要n小时完成,如果两人合做,完成这
件工作的时间是______小时; (2)某食堂有米m公斤,原计划每天用粮a公斤,现在每天节约用粮b公斤,则可以
比原计划多用天数是______; 列分式方程解应用题解方程大显身手(1)(2)2.计算:(1) (-2)-3; 注:负整数次幂:任何不等于零的数的负整数次幂,等于这个数的正整数次幂的倒数。3、计算:分式方程解的情况 X=25X=1或x=-12或0变式3、当a为何值时,方程
的解是正数?变式4、当a为何值时,方程
无解?若解是负数呢?1.若方程 有增根,则增根应是 .
2.解关于x的方程
产生增根,则常数a= 。大显身手X=-2-4或63.当m为何值时,方程 解为非负数?再见
