19.2.3一次函数与方程、不等式 课件(共26张PPT)
文档属性
| 名称 | 19.2.3一次函数与方程、不等式 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1003.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
19.2 函数
19.2.3 一次函数与方程、不等式
新人教版八年级数学下册
学习目标
1.理解一次函数与一元一次方程、一元一次不等式及二元一次方程(组)之间的关系.
2.能用函数的观点解一元一次方程、一元一次不等式及二元一次方程(组).
3.熟练地掌握用数形结合法解一元一次方程、一元一次不等式及二元一次方程(组).
新知导入
看看下面两个问题之间的关系:
(1)解方程:2x+20=0.
(2)自变量x为何值时,函数y=2x+20的值为0?
分析:
可以从下面三个方面思考:
(1)对于2x+20=0和y=2x+20,从形式上看,有什么不同?
(2)从问题的本质上看,(1)和(2)有什么关系?
(3)若作出y=2x+20的图象,(1)和(2)有什么关系?
新知讲解
活动1:探究一次函数与一元一次方程
问题:(1)解方程2x+20=0.
(2)当自变量x为何值时,函数y=2x+20的值为0?
◆对于2x+20=0和y=2x+20,从形式上看,有什么不同?
2x+20=0 y=2x+20
形式上
一元一次方程
一次函数
新知讲解
问题:(1)解方程2x+20=0.
(2)当自变量x为何值时,函数y=2x+20的值为0?
◆从问题的本质上看,有什么不同?
2x+20=0 y=2x+20
本质上
解方程
2x+20=0,
得x=-10
当函数值y为0时,所对应的自变量x的值,也就是:当y=0时,即2x+20=0,解得
x=-10
(从“数”
的角度看)
新知讲解
从“数”上看
序号 一元一次方程问题 一次函数问题
1 解方程2x+20=0 当x为何值时,y=2x+20的值为0?
2 当x为何值时,
y=-2x+20的值为0?
3 解方程-2x+2=-1
4
解方程-2x+20=0
先转化为-2x+3=0
当x为何值时,
y=-2x+3的值为0
解方程ax+b=0
当x为何值时,
y=ax+b的值为0
新知讲解
问题:(1)解方程2x+20=0.
(2)当自变量x为何值时,函数y=2x+20的值为0?
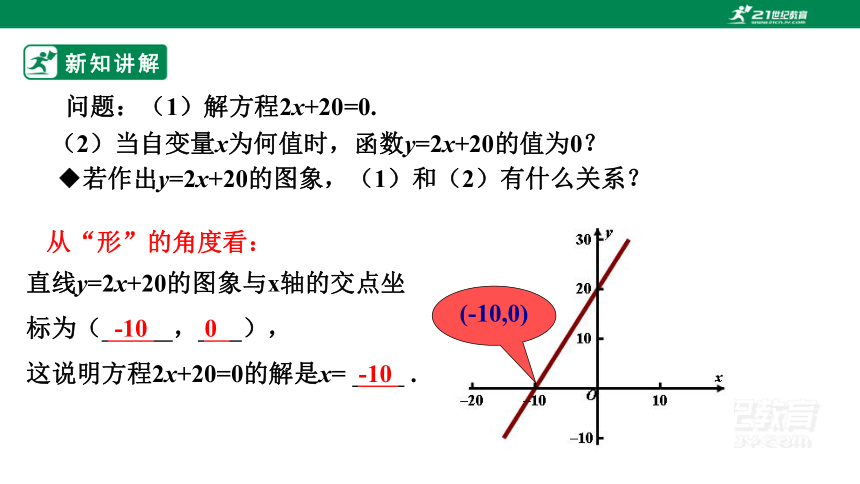
◆若作出y=2x+20的图象,(1)和(2)有什么关系?
从“形”的角度看:
直线y=2x+20的图象与x轴的交点坐标为( -10 , 0 ),
这说明方程2x+20=0的解是x= -10 .
(-10,0)
序号 一次函数问题 图像
1
2
3
4
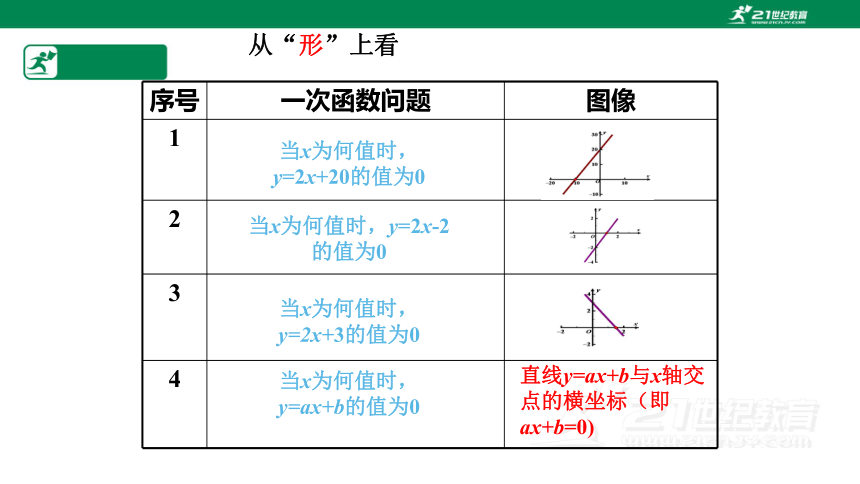
从“形”上看
当x为何值时,y=2x+20的值为0
当x为何值时,y=2x-2的值为0
当x为何值时,y=2x+3的值为0
当x为何值时,y=ax+b的值为0
直线y=ax+b与x轴交点的横坐标(即ax+b=0)
总结
结论:前面两个问题实际上是同一个问题(只是表达形式不同).
一次函数与一元一次方程的关系
求ax+b=0(a,b是
常数,a≠0)的解
从“函数值”看
当x为何值时,
函数y=ax+b的
值为0
求ax+b=0(a,b是
常数,a≠0)的解
从“函数图象”看
求直线y=ax+b
与x轴交点的
横坐标
新知讲解
下面3个方程有什么共同点与不同点?你能从函数的角度对解这3个方程进行解释吗?
(1)2x+1=3
(2)2x+1=0
(3)2x+1=-1
2x+1=0的解
2x+1=3的解
2x+1=0的解
用函数的观点看
解一元一次方程ax+b=k就是求当函数值为k时对应的自变量x的值.
知识要点
◆一元一次方程ax+b=k(a≠0)与函数y=ax+b
一次函数
与一元一
次方程的
关系
求ax+b=k(a≠0)的解
(从“数”的角度)
x为何值时y=ax+b的值为k
(从“形”的角度)
当函数y=ax+b纵坐标为k时,
所对应的横坐标x的值
新知讲解
活动2:探究一次函数与一元一次不等式
从“数”上看
(1)解不等式:2x-4>0;
(2)当x为何值时,函数y=2x-4的值大于0.
解:
(1)解得x>2;
(2)就是要使2x-4>0,解得x>2时函数y=2x-4的值大于0.
在上面的问题解决过程中,你能发现它们之间有什么关系?
议一议:
从数的角度看它们是同一个问题
(1)解不等式3x-6<0,可以看作
求一次函数y=3x-6的函数值小于0的自 变量的取值范围
(2)“当自变量x取何值时,函数y=3x+8的值大于0”可看作
求不等式3x+8>0的解集
新知讲解
从“形”上看
问题3. 如何用函数图象来解释:自变量x为何值时,函数y=2x-4的值大于0
解:
画出直线y=2x-4
x>2
根据下列一次函数的图象,说出对应不等式的解集.
-2
(1)3x+6>0
x>-2
y=3x+6
3
y=-x+3
(2)-x+3≥0
x≤3
思考
(1)3x+2>2;
下面三个不等式有什么共同特点?你能从函数的角度对解这三个不等式进行解释吗?能把你得到的结论推广到一般情形吗?
(2)3x+2<0;
(3)3x+2<-1.
y=2
y=-1
y=3x+2
(1) x>0
(3) x<-1
知识要点
★不等式ax+b>c的解集就是使函数y=ax+b的数值大于c的对应的自变量取值范围;
★不等式ax+by=3x+2
y=2
y=-1
新知讲解
活动3:探究一次函数与二元一次方程组
1.结合前面,你能说说怎样用图象法解二元一次组吗?
写函数,作图象,找交点,下结论
2.如何从图象中找出二元一次方程组的解?
找出方程组所对应的一次函数图象的交点坐标.
归纳总结
从数的角度看:
求二元一次方程组的解
自变量为何值时,两个函数的值相等并求函数值
从形的角度看:
求二元一次方程组的解
是确定两条直线交点的坐标
求二元一次方程组的解
自变量为何值时,两个函数的值相等并求函数值
例题讲解
例 老师为了教学,需要在家上网查资料.电信公司提供了两种上网收费方式:
方式 1 :按上网时间以每分钟 0.1 元计费;
方式 2 :月租费 20 元,再按上网时间以每分钟 0.05 元计费.
请同学们帮老师选择:以何种方式上网更合算?
例题讲解
o
y/元
x /分
20
400
200
y1 =0.1x
y 2=0.05x+20
40
30
在同一坐标系中分别画出这两个函数的图像
当 x = 400 时,
y1 = y2
当 x>400 时,
y1 > y2
当 0≤x<400 时,
y1 < y2
y1=0.1x
y2=0.05x+20
解:设上网时间为 x 分,若按方式 1 则收 元;
若按方式 2 则收 元.
y1=0.1x
y2=0.05x+20
例题讲解
由函数图像得:
当 时,y>0,
即选方式 省钱;
当 时,y=0,
即选方式A、B ;
当 时,y<0,
即选方式 省钱;
400
y=-0.05x+20
20
0
y
x
解法2:设上网时间为 x 分,方式 B与方式 A两种计费的差额为 y元,则 y 随 x 变化的函数关系式为 ________ . 化简得 ____.
在直角坐标系中画出这个函数的图像。
y=(0.05x+20) -0.1x
y=-0.05x +20
0≤x<400
x=400
x>400
A
B
一样
课堂练习
1.在一次函数y=x-9中,要得到y=-2,则x应取( )
A.-7 B.7 C.11 D.-11
2.若一次函数y=kx+b图象与x轴相交点(3,0),则kx+b=0的解为( )
A.x=-3 B. x=3 C. x=0 D. 不能确定
3.如图,函数y=ax+b与y=kx-c的图象相交于点P,则根据图象可得二元一次方程组
的解是 .
4.已知方程ax+b=0的解是-2,下列图像肯定不是直线y=ax+b的是( )
A
课堂总结
用函数的观点看,解一元一次方程ax+b=k就是求当函数值为k时对应的自变量x的值.
不等式ax+b>c的解集就是使函数y=ax+b的数值大于c的对应的自变量取值范围;反之,为小于.
方程的解
直线上的点的坐标
方程组的解
直线交点的坐标
作业布置
1.如图,直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集在数轴上表示正确的是( )
A.
B.
C.
D.
2. 如图,直线l1:y=k1x+b与直线l2:y=k2x+c在同一平面直角坐标系中的图象如图所示,则关于x的方程k1x+b=k2x+c的解x=____________.
3.如图,直线y=kx+b过A(-1,2)、B(-2,0)两点,则0≤kx+b≤-2x的解集为________.
4.如图,一次函数y=-x+m的图象和y轴交于点B,与正比例函数y= 图象交于点P(2,n).
(1)求m和n的值;
(2)求△POB的面积.
谢谢
19.2 函数
19.2.3 一次函数与方程、不等式
新人教版八年级数学下册
学习目标
1.理解一次函数与一元一次方程、一元一次不等式及二元一次方程(组)之间的关系.
2.能用函数的观点解一元一次方程、一元一次不等式及二元一次方程(组).
3.熟练地掌握用数形结合法解一元一次方程、一元一次不等式及二元一次方程(组).
新知导入
看看下面两个问题之间的关系:
(1)解方程:2x+20=0.
(2)自变量x为何值时,函数y=2x+20的值为0?
分析:
可以从下面三个方面思考:
(1)对于2x+20=0和y=2x+20,从形式上看,有什么不同?
(2)从问题的本质上看,(1)和(2)有什么关系?
(3)若作出y=2x+20的图象,(1)和(2)有什么关系?
新知讲解
活动1:探究一次函数与一元一次方程
问题:(1)解方程2x+20=0.
(2)当自变量x为何值时,函数y=2x+20的值为0?
◆对于2x+20=0和y=2x+20,从形式上看,有什么不同?
2x+20=0 y=2x+20
形式上
一元一次方程
一次函数
新知讲解
问题:(1)解方程2x+20=0.
(2)当自变量x为何值时,函数y=2x+20的值为0?
◆从问题的本质上看,有什么不同?
2x+20=0 y=2x+20
本质上
解方程
2x+20=0,
得x=-10
当函数值y为0时,所对应的自变量x的值,也就是:当y=0时,即2x+20=0,解得
x=-10
(从“数”
的角度看)
新知讲解
从“数”上看
序号 一元一次方程问题 一次函数问题
1 解方程2x+20=0 当x为何值时,y=2x+20的值为0?
2 当x为何值时,
y=-2x+20的值为0?
3 解方程-2x+2=-1
4
解方程-2x+20=0
先转化为-2x+3=0
当x为何值时,
y=-2x+3的值为0
解方程ax+b=0
当x为何值时,
y=ax+b的值为0
新知讲解
问题:(1)解方程2x+20=0.
(2)当自变量x为何值时,函数y=2x+20的值为0?
◆若作出y=2x+20的图象,(1)和(2)有什么关系?
从“形”的角度看:
直线y=2x+20的图象与x轴的交点坐标为( -10 , 0 ),
这说明方程2x+20=0的解是x= -10 .
(-10,0)
序号 一次函数问题 图像
1
2
3
4
从“形”上看
当x为何值时,y=2x+20的值为0
当x为何值时,y=2x-2的值为0
当x为何值时,y=2x+3的值为0
当x为何值时,y=ax+b的值为0
直线y=ax+b与x轴交点的横坐标(即ax+b=0)
总结
结论:前面两个问题实际上是同一个问题(只是表达形式不同).
一次函数与一元一次方程的关系
求ax+b=0(a,b是
常数,a≠0)的解
从“函数值”看
当x为何值时,
函数y=ax+b的
值为0
求ax+b=0(a,b是
常数,a≠0)的解
从“函数图象”看
求直线y=ax+b
与x轴交点的
横坐标
新知讲解
下面3个方程有什么共同点与不同点?你能从函数的角度对解这3个方程进行解释吗?
(1)2x+1=3
(2)2x+1=0
(3)2x+1=-1
2x+1=0的解
2x+1=3的解
2x+1=0的解
用函数的观点看
解一元一次方程ax+b=k就是求当函数值为k时对应的自变量x的值.
知识要点
◆一元一次方程ax+b=k(a≠0)与函数y=ax+b
一次函数
与一元一
次方程的
关系
求ax+b=k(a≠0)的解
(从“数”的角度)
x为何值时y=ax+b的值为k
(从“形”的角度)
当函数y=ax+b纵坐标为k时,
所对应的横坐标x的值
新知讲解
活动2:探究一次函数与一元一次不等式
从“数”上看
(1)解不等式:2x-4>0;
(2)当x为何值时,函数y=2x-4的值大于0.
解:
(1)解得x>2;
(2)就是要使2x-4>0,解得x>2时函数y=2x-4的值大于0.
在上面的问题解决过程中,你能发现它们之间有什么关系?
议一议:
从数的角度看它们是同一个问题
(1)解不等式3x-6<0,可以看作
求一次函数y=3x-6的函数值小于0的自 变量的取值范围
(2)“当自变量x取何值时,函数y=3x+8的值大于0”可看作
求不等式3x+8>0的解集
新知讲解
从“形”上看
问题3. 如何用函数图象来解释:自变量x为何值时,函数y=2x-4的值大于0
解:
画出直线y=2x-4
x>2
根据下列一次函数的图象,说出对应不等式的解集.
-2
(1)3x+6>0
x>-2
y=3x+6
3
y=-x+3
(2)-x+3≥0
x≤3
思考
(1)3x+2>2;
下面三个不等式有什么共同特点?你能从函数的角度对解这三个不等式进行解释吗?能把你得到的结论推广到一般情形吗?
(2)3x+2<0;
(3)3x+2<-1.
y=2
y=-1
y=3x+2
(1) x>0
(3) x<-1
知识要点
★不等式ax+b>c的解集就是使函数y=ax+b的数值大于c的对应的自变量取值范围;
★不等式ax+b
y=2
y=-1
新知讲解
活动3:探究一次函数与二元一次方程组
1.结合前面,你能说说怎样用图象法解二元一次组吗?
写函数,作图象,找交点,下结论
2.如何从图象中找出二元一次方程组的解?
找出方程组所对应的一次函数图象的交点坐标.
归纳总结
从数的角度看:
求二元一次方程组的解
自变量为何值时,两个函数的值相等并求函数值
从形的角度看:
求二元一次方程组的解
是确定两条直线交点的坐标
求二元一次方程组的解
自变量为何值时,两个函数的值相等并求函数值
例题讲解
例 老师为了教学,需要在家上网查资料.电信公司提供了两种上网收费方式:
方式 1 :按上网时间以每分钟 0.1 元计费;
方式 2 :月租费 20 元,再按上网时间以每分钟 0.05 元计费.
请同学们帮老师选择:以何种方式上网更合算?
例题讲解
o
y/元
x /分
20
400
200
y1 =0.1x
y 2=0.05x+20
40
30
在同一坐标系中分别画出这两个函数的图像
当 x = 400 时,
y1 = y2
当 x>400 时,
y1 > y2
当 0≤x<400 时,
y1 < y2
y1=0.1x
y2=0.05x+20
解:设上网时间为 x 分,若按方式 1 则收 元;
若按方式 2 则收 元.
y1=0.1x
y2=0.05x+20
例题讲解
由函数图像得:
当 时,y>0,
即选方式 省钱;
当 时,y=0,
即选方式A、B ;
当 时,y<0,
即选方式 省钱;
400
y=-0.05x+20
20
0
y
x
解法2:设上网时间为 x 分,方式 B与方式 A两种计费的差额为 y元,则 y 随 x 变化的函数关系式为 ________ . 化简得 ____.
在直角坐标系中画出这个函数的图像。
y=(0.05x+20) -0.1x
y=-0.05x +20
0≤x<400
x=400
x>400
A
B
一样
课堂练习
1.在一次函数y=x-9中,要得到y=-2,则x应取( )
A.-7 B.7 C.11 D.-11
2.若一次函数y=kx+b图象与x轴相交点(3,0),则kx+b=0的解为( )
A.x=-3 B. x=3 C. x=0 D. 不能确定
3.如图,函数y=ax+b与y=kx-c的图象相交于点P,则根据图象可得二元一次方程组
的解是 .
4.已知方程ax+b=0的解是-2,下列图像肯定不是直线y=ax+b的是( )
A
课堂总结
用函数的观点看,解一元一次方程ax+b=k就是求当函数值为k时对应的自变量x的值.
不等式ax+b>c的解集就是使函数y=ax+b的数值大于c的对应的自变量取值范围;反之,为小于.
方程的解
直线上的点的坐标
方程组的解
直线交点的坐标
作业布置
1.如图,直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集在数轴上表示正确的是( )
A.
B.
C.
D.
2. 如图,直线l1:y=k1x+b与直线l2:y=k2x+c在同一平面直角坐标系中的图象如图所示,则关于x的方程k1x+b=k2x+c的解x=____________.
3.如图,直线y=kx+b过A(-1,2)、B(-2,0)两点,则0≤kx+b≤-2x的解集为________.
4.如图,一次函数y=-x+m的图象和y轴交于点B,与正比例函数y= 图象交于点P(2,n).
(1)求m和n的值;
(2)求△POB的面积.
谢谢
