2.2.2用样本的数字特征估计总体的数字特征(下)
文档属性
| 名称 | 2.2.2用样本的数字特征估计总体的数字特征(下) |  | |
| 格式 | zip | ||
| 文件大小 | 128.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-25 19:58:32 | ||
图片预览








文档简介
课件23张PPT。方差与标准差 湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作2.2.2 用样本的数字特征估计总体的数字特征(下)目标导学1、通过实例理解样本数据标准差的意义,会计算样本平均数和标准差。
2、体会用样本估计总体的思想,会用样本的基本数字特征(平均数、标准差)估计总体的基本数字特征。 平均数向我们提供了样本数据的重要信息,但是平均有时也会使我们作出对总体的片面判断.因为这个平均数掩盖了一些极端的情况,而这些极端情况显然是不能忽的.因此,只有平均数还难以概括样本数据的实际状态.如:有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:甲:7 8 7 9 5 4 9 10 7 4乙:9 5 7 8 7 6 8 6 7 7如果你是教练,你应当如何对这次射击作出评价?如果看两人本次射击的平均成绩,由于 两人射击 的平均成绩是一样的.那么两个人的水平就没有什么差异吗?
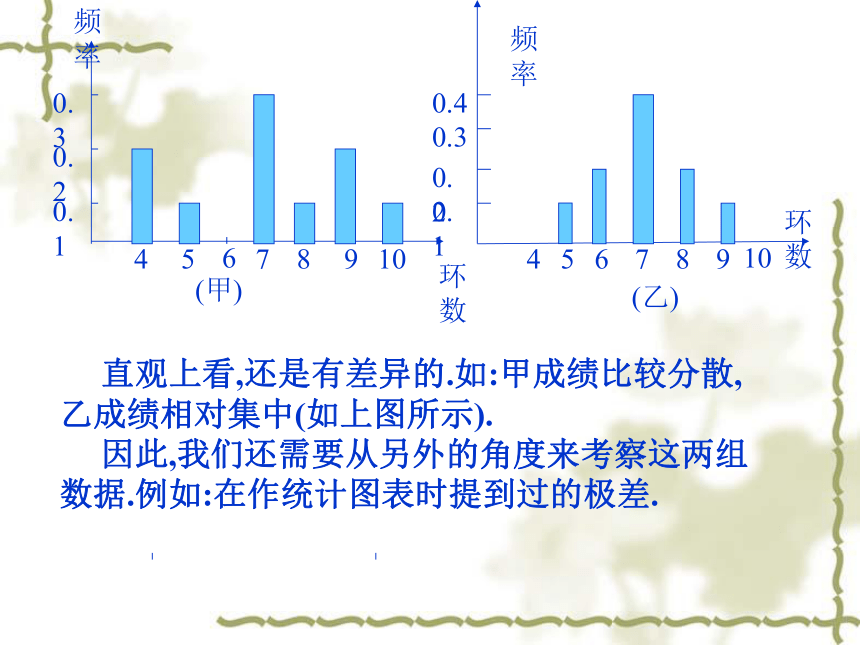
(甲)45678910环数频率0.10.20.3频率(乙) 直观上看,还是有差异的.如:甲成绩比较分散,乙成绩相对集中(如上图所示).
因此,我们还需要从另外的角度来考察这两组数据.例如:在作统计图表时提到过的极差.
甲的环数极差=10-4=6 乙的环数极差=9-5=4.
它们在一定程度上表明了样本数据的分散程度,与平均数一起,可以给我们许多关于样本数据的信息.显然,极差对极端值非常敏感,注意到这一点,我们可以得到一种“去掉一个最高分,去掉一个最低分”的统计策略. 考察样本数据的分散程度的大小,最常用的统计量是标准差.
标准差是样本平均数的一种平均距离,一般用s表示.所谓“平均距离”,其含义可作如下理解: 由于上式含有绝对值,运算不太方便,因此,通常改用如下公式来计算标准差.一个样本中的个体与平均数之间的距离关系可用下图表示:考虑一个容量为2的样本:极差:一组数据的最大值与最小值的差极差越大,数据越分散,越不稳定极差越小,数据越集中,越稳定极差体现了数据的离散程度(即波动大小)设一组样本数据 ,其平均数为 ,则称s2为这个样本的方差,称为这个样本的标准差,分别称为样本方差、样本标准差它的算术平方根样本中各数据与样本平均数的差的平方和的平均数叫做样本方差;样本方差的算术平方根叫做样本标准差。样本方差和样本标准差都是衡量一个样本波动大小的量,样本方差或样本标准差越大,样本数据的波动就越大。 1、在一次歌手大奖赛上,七位评委为歌手打出的分数
如下:
9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分
和一个最低分后,所剩数据的平均值和方差分别为
_________________; 9.5,0.016 解:平均数是6,方差是8,标准差是 .去掉最高分和最低分合理吗? 3、求 的平均数、方差、标准差。
(1)甲、乙两名战士在射击训练中,打靶的次数相同,且射击成绩的平均数也相同,如果甲的射击成绩比较稳定,那么方差的大小关系是: S2甲_________S2乙。做一做:<做一做:(2)小明和小聪最近5次数学测验成绩如下:哪位同学的数学成绩比较稳定?乙例题1:画出下列四组样本数据的直方图,说明它们的异同点.解:四组样本数据的直方图是:四组数据的平均数都是5.0,标准差分别是0.00,0.82,1.49,2.83.
虽然它们有相同的平均数,但是它们有不同的标准差,说明数据的分散程度是不一样的.所以 显然,标准差越大,则a越大,数据的离散程度越大;标准差越小,数据的离散程度越小.用计算器可算出甲,乙两人的的成绩的标准差上面两组数据的离散程度与标准差之间的关系可用图直观地表示出来.例2 甲乙两人同时生产内径为25.40mm的一种零件.为了对两人的生产质量进行评比,从他们生产的零件中各抽出20件,量得其内径尺寸如下(单位:mm)甲 25.46, 25.32, 25.45, 25.39, 25.36
25.34, 25.42, 25.45, 25.38, 25.42
25.39, 25.43, 25.39, 25.40, 25.44
25.40, 25.42, 25.35, 25.41, 25.39乙 25.40, 25.43, 25.44, 25.48, 25.48
25.47, 25.49, 25.49, 25.36, 25.34
25.33, 25.43, 25.43, 25.32, 25.47
25.31, 25.32, 25.32, 25.32, 25.48 从生产的零件内径的尺寸看,谁生产的质量较高?分析:每一个工人生产的所有零件的内径尺寸组成一个总体,
由于零件的生产标准已经给出(内径25.40mm),生产质量可以从总体的平均数与标准差两个角度来衡量.总体的平均数与内径标准尺寸25.00mm的差异在时质量低,差异小时质量高;当总体的平均数与标准尺寸很接近时,总体的标准差小的时候质量高,标准差大的时候质量低.这样比较两人的生产质量只要比较他们所生产的零件内径尺寸所组成的两个总体的平均数与标准差的大小即可.但是这两个总体的平均数与标准差都是不知道的,根据用样本估计总体的思想,我们可以通过抽样分别获得相应的样体数据,然后比较这两个样本的平均数,标准差,以此作为两个总体之间的估计值.解:用计算器计算可得: 从样本平均数看,甲生产的零件内径比乙生产的更接近内径标准(25.40mm),但是差异很小;从样本标准差看,由于 从上述例子我们可以看到,对一名工人生产的零件内径(总体)的质量判断,与我们抽取的内径(样本数据)直接相关.显然,我们可以从这名工人生产的零件中获取许多样本(为什么?).这样,尽管总体是同一个,但由于样本不同,相应的样本频率分布与平均数,标准差等都会发生改变,这就会影响到我们对总体情况的估计.如果样本的的代表性差,那么对总体所作出的估计就会产生偏差;样本没有代表性时,对总体作出错误估计的可能性就非常大.这也正是我们在前面讲随机抽样时反复强调样本代表性的理由.在实际操作中,为了减少错误的发生,条件许可时,通常采取适当增加样本容量的方法.当然,关键还是要改进抽样方法,提高样本的代表性.极差、方差、标准差有什么区别和联系?
联系:极差、方差和标准差都能用来描述数据的离散程度.
区别:(1)极差是数据的最大值与最小值的差.它反映了一组数据变化的最大幅度,它对一组数据中的极端值非常敏感.
(2)方差则反映了一组数据围绕平均数波动的大小.为了得到以样本数据的单位表示的波动幅度通常用标准差,即样本方差的算术平方根,是样本数据到平均数的一种平均距离.
注:已知ai的平均数X、方差Y、标准差Z,
则b+kai的平均数是b+kx, 方差是k的平方与Y的乘积,
标准差是k与Z的乘积。(当然Y=Z的平方!)小结1、极差、方差、标准差是体现数据离散程度,即波动大小。
2、实际解题中,经常是先由平均数了解两组数据的情况,再计算方差来说明两组数据的稳定性好坏。作业:
P82习题2.2 A组:5,6.
B组:1.1、从高一(1)班的一次数学测验抽取一小组 成绩如下(保留整数):85 90 80 80 85 75 100 计算这组样本数据的极差、方差和标准差.2、甲、乙两种水稻试验品种连续5年的平均
单位面积产量如下(单位:t/hm2),试根据
这组数据估计哪一种水稻品种的产量比较稳定。
课后练习:3.为了保护学生的视力,教室内的日光灯在
使用一段时间后必须更换。已知某校使用的100
只日光灯在必须换掉前的使用天数如下,试估计
这种日光灯的平均使用寿命和标准差。
高中数学老师欧阳文丰制作2.2.2 用样本的数字特征估计总体的数字特征(下)目标导学1、通过实例理解样本数据标准差的意义,会计算样本平均数和标准差。
2、体会用样本估计总体的思想,会用样本的基本数字特征(平均数、标准差)估计总体的基本数字特征。 平均数向我们提供了样本数据的重要信息,但是平均有时也会使我们作出对总体的片面判断.因为这个平均数掩盖了一些极端的情况,而这些极端情况显然是不能忽的.因此,只有平均数还难以概括样本数据的实际状态.如:有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:甲:7 8 7 9 5 4 9 10 7 4乙:9 5 7 8 7 6 8 6 7 7如果你是教练,你应当如何对这次射击作出评价?如果看两人本次射击的平均成绩,由于 两人射击 的平均成绩是一样的.那么两个人的水平就没有什么差异吗?
(甲)45678910环数频率0.10.20.3频率(乙) 直观上看,还是有差异的.如:甲成绩比较分散,乙成绩相对集中(如上图所示).
因此,我们还需要从另外的角度来考察这两组数据.例如:在作统计图表时提到过的极差.
甲的环数极差=10-4=6 乙的环数极差=9-5=4.
它们在一定程度上表明了样本数据的分散程度,与平均数一起,可以给我们许多关于样本数据的信息.显然,极差对极端值非常敏感,注意到这一点,我们可以得到一种“去掉一个最高分,去掉一个最低分”的统计策略. 考察样本数据的分散程度的大小,最常用的统计量是标准差.
标准差是样本平均数的一种平均距离,一般用s表示.所谓“平均距离”,其含义可作如下理解: 由于上式含有绝对值,运算不太方便,因此,通常改用如下公式来计算标准差.一个样本中的个体与平均数之间的距离关系可用下图表示:考虑一个容量为2的样本:极差:一组数据的最大值与最小值的差极差越大,数据越分散,越不稳定极差越小,数据越集中,越稳定极差体现了数据的离散程度(即波动大小)设一组样本数据 ,其平均数为 ,则称s2为这个样本的方差,称为这个样本的标准差,分别称为样本方差、样本标准差它的算术平方根样本中各数据与样本平均数的差的平方和的平均数叫做样本方差;样本方差的算术平方根叫做样本标准差。样本方差和样本标准差都是衡量一个样本波动大小的量,样本方差或样本标准差越大,样本数据的波动就越大。 1、在一次歌手大奖赛上,七位评委为歌手打出的分数
如下:
9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分
和一个最低分后,所剩数据的平均值和方差分别为
_________________; 9.5,0.016 解:平均数是6,方差是8,标准差是 .去掉最高分和最低分合理吗? 3、求 的平均数、方差、标准差。
(1)甲、乙两名战士在射击训练中,打靶的次数相同,且射击成绩的平均数也相同,如果甲的射击成绩比较稳定,那么方差的大小关系是: S2甲_________S2乙。做一做:<做一做:(2)小明和小聪最近5次数学测验成绩如下:哪位同学的数学成绩比较稳定?乙例题1:画出下列四组样本数据的直方图,说明它们的异同点.解:四组样本数据的直方图是:四组数据的平均数都是5.0,标准差分别是0.00,0.82,1.49,2.83.
虽然它们有相同的平均数,但是它们有不同的标准差,说明数据的分散程度是不一样的.所以 显然,标准差越大,则a越大,数据的离散程度越大;标准差越小,数据的离散程度越小.用计算器可算出甲,乙两人的的成绩的标准差上面两组数据的离散程度与标准差之间的关系可用图直观地表示出来.例2 甲乙两人同时生产内径为25.40mm的一种零件.为了对两人的生产质量进行评比,从他们生产的零件中各抽出20件,量得其内径尺寸如下(单位:mm)甲 25.46, 25.32, 25.45, 25.39, 25.36
25.34, 25.42, 25.45, 25.38, 25.42
25.39, 25.43, 25.39, 25.40, 25.44
25.40, 25.42, 25.35, 25.41, 25.39乙 25.40, 25.43, 25.44, 25.48, 25.48
25.47, 25.49, 25.49, 25.36, 25.34
25.33, 25.43, 25.43, 25.32, 25.47
25.31, 25.32, 25.32, 25.32, 25.48 从生产的零件内径的尺寸看,谁生产的质量较高?分析:每一个工人生产的所有零件的内径尺寸组成一个总体,
由于零件的生产标准已经给出(内径25.40mm),生产质量可以从总体的平均数与标准差两个角度来衡量.总体的平均数与内径标准尺寸25.00mm的差异在时质量低,差异小时质量高;当总体的平均数与标准尺寸很接近时,总体的标准差小的时候质量高,标准差大的时候质量低.这样比较两人的生产质量只要比较他们所生产的零件内径尺寸所组成的两个总体的平均数与标准差的大小即可.但是这两个总体的平均数与标准差都是不知道的,根据用样本估计总体的思想,我们可以通过抽样分别获得相应的样体数据,然后比较这两个样本的平均数,标准差,以此作为两个总体之间的估计值.解:用计算器计算可得: 从样本平均数看,甲生产的零件内径比乙生产的更接近内径标准(25.40mm),但是差异很小;从样本标准差看,由于 从上述例子我们可以看到,对一名工人生产的零件内径(总体)的质量判断,与我们抽取的内径(样本数据)直接相关.显然,我们可以从这名工人生产的零件中获取许多样本(为什么?).这样,尽管总体是同一个,但由于样本不同,相应的样本频率分布与平均数,标准差等都会发生改变,这就会影响到我们对总体情况的估计.如果样本的的代表性差,那么对总体所作出的估计就会产生偏差;样本没有代表性时,对总体作出错误估计的可能性就非常大.这也正是我们在前面讲随机抽样时反复强调样本代表性的理由.在实际操作中,为了减少错误的发生,条件许可时,通常采取适当增加样本容量的方法.当然,关键还是要改进抽样方法,提高样本的代表性.极差、方差、标准差有什么区别和联系?
联系:极差、方差和标准差都能用来描述数据的离散程度.
区别:(1)极差是数据的最大值与最小值的差.它反映了一组数据变化的最大幅度,它对一组数据中的极端值非常敏感.
(2)方差则反映了一组数据围绕平均数波动的大小.为了得到以样本数据的单位表示的波动幅度通常用标准差,即样本方差的算术平方根,是样本数据到平均数的一种平均距离.
注:已知ai的平均数X、方差Y、标准差Z,
则b+kai的平均数是b+kx, 方差是k的平方与Y的乘积,
标准差是k与Z的乘积。(当然Y=Z的平方!)小结1、极差、方差、标准差是体现数据离散程度,即波动大小。
2、实际解题中,经常是先由平均数了解两组数据的情况,再计算方差来说明两组数据的稳定性好坏。作业:
P82习题2.2 A组:5,6.
B组:1.1、从高一(1)班的一次数学测验抽取一小组 成绩如下(保留整数):85 90 80 80 85 75 100 计算这组样本数据的极差、方差和标准差.2、甲、乙两种水稻试验品种连续5年的平均
单位面积产量如下(单位:t/hm2),试根据
这组数据估计哪一种水稻品种的产量比较稳定。
课后练习:3.为了保护学生的视力,教室内的日光灯在
使用一段时间后必须更换。已知某校使用的100
只日光灯在必须换掉前的使用天数如下,试估计
这种日光灯的平均使用寿命和标准差。
