5.7三角函数的应用 同步练习(Word版含解析)
文档属性
| 名称 | 5.7三角函数的应用 同步练习(Word版含解析) | 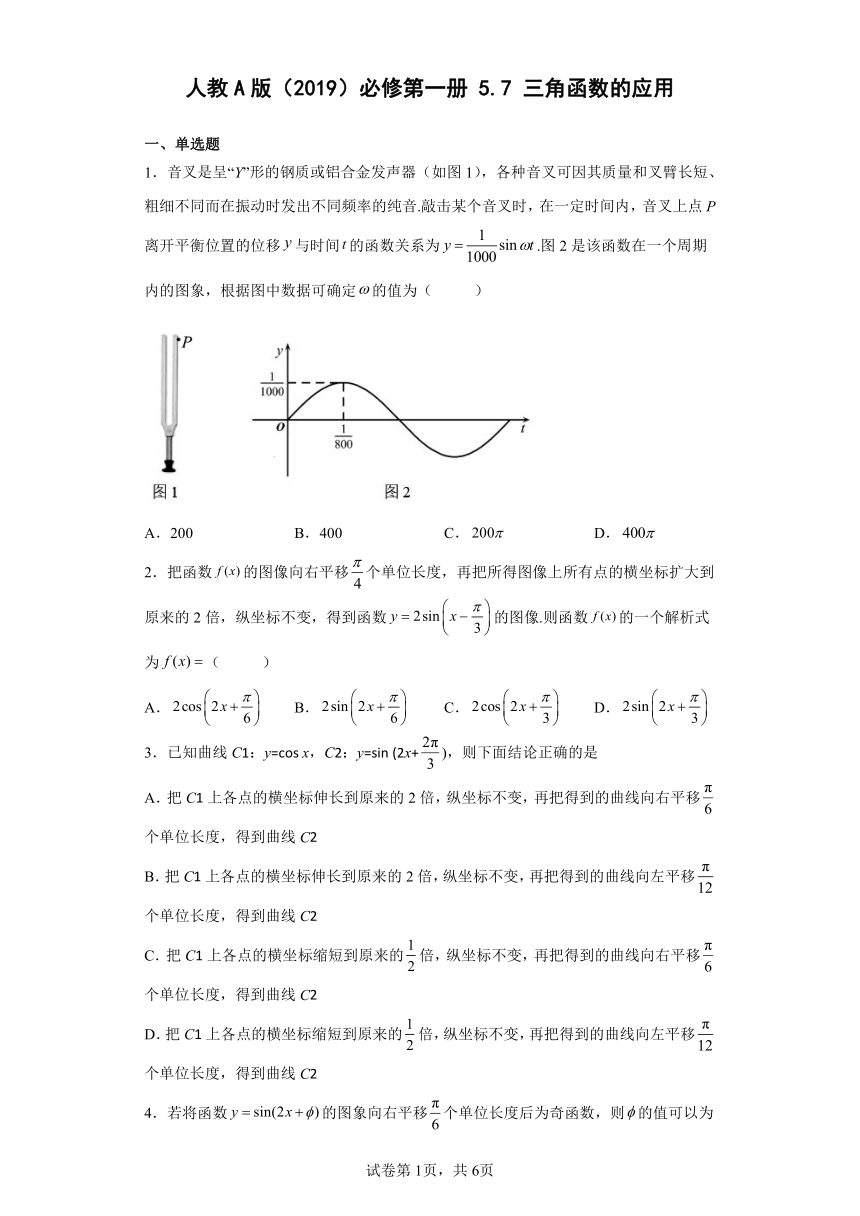 | |
| 格式 | docx | ||
| 文件大小 | 760.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 04:58:33 | ||
图片预览




文档简介
人教A版(2019)必修第一册 5.7 三角函数的应用
一、单选题
1.音叉是呈“Y”形的钢质或铝合金发声器(如图1),各种音叉可因其质量和叉臂长短、粗细不同而在振动时发出不同频率的纯音.敲击某个音叉时,在一定时间内,音叉上点P离开平衡位置的位移与时间的函数关系为.图2是该函数在一个周期内的图象,根据图中数据可确定的值为( )
A.200 B.400 C. D.
2.把函数的图像向右平移个单位长度,再把所得图像上所有点的横坐标扩大到原来的2倍,纵坐标不变,得到函数的图像.则函数的一个解析式为( )
A. B. C. D.
3.已知曲线C1:y=cos x,C2:y=sin (2x+),则下面结论正确的是
A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2
C.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2
D.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2
4.若将函数的图象向右平移个单位长度后为奇函数,则的值可以为( )
A. B. C. D.
5.已知简谐振动的振幅是,图象上相邻最高点和最低点的距离是5,且过点,则该简谐振动的频率和初相是( )
A., B.,
C., D.,
6.如图,某大楼AB旁有一山坡,其斜坡CD的坡度(或坡比),山坡坡面上点E处有一休息亭.某数学兴趣小组测得山坡坡脚C与大楼水平距离米,与休息亭距离米,并从E点测得大楼顶部点的仰角为,点A,B,C,D,E在同一平面内,则大楼AB的高度约为( )
(结果精确到0.1米;参考数据:,,)
A.89.0米 B.74.2米 C.74.0米 D.59.2米
7.为了得到函数的图象,可将的图象( )
A.向右平移个单位 B.向右平移个单位
C.向左平移个单位 D.向左平移个单位
8.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用.如图,一个半径为的筒车按逆时针方向每分钟转圈,筒车的轴心距离水面的高度为米.设筒车上的某个盛水筒到水面的距离为(单位:)(在水面下则为负数),若以盛水筒刚浮出水面时开始计算时间,则与时间(单位:)之间的关系为.则盛水筒出水后到达最高点的最少时间为( )
A. B. C. D.
9.已知函数的最小正周期为,将其图象向右平移个单位后得函数的图象,则函数的图象
A.关于直线对称 B.关于直线对称
C.关于点对称 D.关于点对称
10.若函数的图象向右平移个单位得到的图象对应的函数为,则下列说法正确的是( )
A.的图象关于对称 B.在上有2个零点
C.在区间上单调递减 D.在上的值域为
11.如图,一个摩天轮的半径为10m,轮子的最低处距离地面2m.如果此摩天轮按逆时针匀速转动,每30分钟转一圈,且当摩天轮上某人经过点(点与摩天轮天轮中心的高度相同)时开始计时,在摩天轮转动的一圈内,此人相对于地面的高度不小于17m的时间大约是( )
A.8分钟 B.10分钟 C.12分钟 D.14分钟
12.如图为一直径为m的水轮,水轮圆心距水面m,已知水轮每分钟转2圈,水轮上的点到水面的距离(m)与时间(s)满足关系是表示表示在水面下,则有( )
A. B.
C. D.
二、填空题
13.如图所示,一半径为4米的水轮,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动一圈,如果当水轮上点P从水中浮现时(图中点)开始计时,则点P第一次到达最高点需要___________秒.
14.函数y=sinωx(ω>0)的部分图象如图所示,点A,B是最高点,点C是最低点,若△ABC是直角三角形,则ω的值为____.
15.海水受日月的引カ,在一定的时候发生涨落的现象叫潮汐.一般早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋.下面是某港口在某季节某天的时间与水深值(单位:m)记录表.
时刻 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
水深值 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 5.0
试用一个三角函数来近似地描述这个港口的水深值y与时间的函数关系,则这个函数关系式是________.
16.某星星的亮度变化周期为10天,此星星的平均亮度为3.8星等,最高亮度距离平均亮度0.2星等,则可近似地描述此星星的亮度与时间之间关系的一个三角函数为________.
17.在电流强度与时间的关系中,要使t在任意的时间内电流强度I能取得最大值A与最小值,则正整数的最小值为________.
三、解答题
18.当我们所处的北半球为冬季的时候,新西兰的惠灵顿市恰好是盛夏,因此北半球的人们冬天愿意去那里旅游,下面是一份惠灵顿机场提供的月平均气温统计表.
(月份) 1 2 3 4 5 6 7 8 9 10 11 12
17.3 17.9 17.3 15.8 13.7 11.6 10.06 9.5 10.06 11.6 13.7 15.8
(1)根据这个统计表提供的数据,为惠灵顿市的月平均气温作出一个函数模型;
(2)当自然气温不低于13.7℃时,惠灵顿市最适宜旅游,试根据你所确定的函数模型,确定惠灵顿市的最佳旅游时间.
19.如图所示,莱蒙都会小区为美化环境,准备在小区内草坪的一侧修建一条直路OC,另一侧修建一条休闲大道.休闲大道的前一段OD是函数的图像的一部分,后一段DBC是函数,(,,,)的图像,图像的最高点为,且,垂足为点.
(1)求函数,(,,,)的解析式;
(2)若在草坪内修建如图所示的矩形儿童乐园 (阴影部分),点P在曲线OD上,其横坐标为,点在上,求儿童乐园的面积.
20.如图,某海港一天从的水位高度(单位:)随时间(单位:)的变化近似满足函数.
(1)求该函数的解析式;
(2)若该海港在水位高度不低于时为轮船最佳进港时间,那么该海港在,轮船最佳进港时间总共多少小时?
21.一根细线的一端固定,另一端悬挂一个小球,当小球来回摆动时,离开平衡位置的位移S(单位:cm)与时间t(单位:s)的函数关系是S=6sin.
(1)画出它的图象;
(2)回答以下问题:
①小球开始摆动(即t=0),离开平衡位置是多少?
②小球摆动时,离开平衡位置的最大距离是多少?
③小球来回摆动一次需要多少时间?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
根据函数图像,确定函数周期,从而可得的值.
【详解】
由图像可得,,,即,则.
故选:D.
本题主要考查三角函数的应用,考查正弦型函数的周期性,属于基础题型.
2.B
将函数的图像所有点的横坐标缩短到原来的,纵坐标不变,再向左平移个单位长度即得解.
【详解】
解:将函数的图像所有点的横坐标缩短到原来的,纵坐标不变,得到,再把函数的图象向左平移个单位长度,得到.
故选:B
3.D
【详解】
把C1上各点的横坐标缩短到原来的倍,纵坐标不变,得到函数y=cos2x图象,再把得到的曲线向左平移个单位长度,得到函数y=cos2(x+)=cos(2x+)=sin(2x+)的图象,即曲线C2,
故选D.
点睛:三角函数的图象变换,提倡“先平移,后伸缩”,但“先伸缩,后平移”也常出现在题目中,所以也必须熟练掌握.无论是哪种变形,切记每一个变换总是对字母而言. 函数是奇函数;函数是偶函数;函数是奇函数;函数是偶函数.
4.C
先由平移公式得出平移后的函数为,由该函数为奇函数可得答案.
【详解】
函数的图象向右平移个单位长度后可得
由题意为奇函数,则
所以,
对照分析答案,当时,
故选:C
5.C
根据正弦型函数的图象与性质求出振幅、周期,再由过点求出初相即可得解.
【详解】
由题意可知,A=,32+2=52,
则T=8,ω==,
y=sin.
由sin φ=,得sin φ=.
∵|φ|<,
∴φ=.
因此频率是,初相为.
故选:C
6.A
过点分别作底面,,然后根据题意分别求出,最后相加即可求出答案.
【详解】
如图,过点作底面垂线,于,
因为斜坡CD的坡度,所以
设,,在中,,即,
解得,则,
所以,
因为在E点测得大楼顶部点的仰角为,
所以
,
故选:A
7.A
将函数化为,根据图象平移变换可得结果.
【详解】
由题意得:
向右平移个单位即可得到的图象
故选:A.
该题考查的是三角函数的平移变换问题,关键是能够理解平移的量是自变量本身的变化量,属于基础题目.
8.D
由已知可得、、、的值,得到函数解析式,取求得的值即可.
【详解】
解:筒车按逆时针方向每分钟转1.5圈,,
则,振幅为筒车的半径,即,,
由题意,时,,,即,
,.
则,
由,得,,
,,得,.
当时,取最小值为.
故选:.
9.D
【详解】
由题意得,故,
∴,
∴,
∴,
∴.
∵,,
∴选项A,B不正确.
又,
,
∴选项C,不正确,选项D正确.选D.
10.B
求出的解析式,并整理后,根据正弦函数性质判断.
【详解】
由题意,
不是函数的最值,不是对称轴,A错;
由,,,其中是上的零点,B正确;
由得,,因此在是递减,在上递增,C错;
时,,,D错.
故选:B.
本题考查三角函数图象变换,考查三角函数的性质.掌握正弦函数性质是解题关键.
11.B
由题可得此人相对于地面的高度与时间的关系是,再令求出的范围即可得出.
【详解】
设时间为时,此人相对于地面的高度为,
则由题可得当时,,
在时间时,此人转过的角为,
此时此人相对于地面的高度,
令,则,
所以,解得,
故在摩天轮转动的一圈内,此人相对于地面的高度不小于17m的时间大约是.
故选:B.
本题考查三角函数的实际应用,解题的关键是得出高度与时间的关系,再解三角函数不等式即可.
12.A
根据题意可得出的值,以及该函数的最小正周期,利用周期公式可求得的值,进而得出结论.
【详解】
由题意可知为水轮的半径3,又水轮每分钟转2圈,故该函数的最小正周期为,所以.
故选:A.
本题考查三角函数解析式中参数的计算,考查计算能力,属于基础题.
13.20
根据题意,计算弧占圆周的比例即可得答案.
【详解】
如图,根据题意得,
所以在中,,
所以,故弧的长为三分之一的圆周长,
又因为水轮每60秒逆时针转动一圈,
所以当水轮上点P从水中浮现时(图中点P)开始计时,则点P第一次到达最高点需要20秒.
故答案为:20
14.
可得△ABC为等腰直角三角形,进而可得AB=2CD=4,还可得AB,解方程可得ω的值.
【详解】
解:由题意结合三角函数的对称性可知△ABC为等腰直角三角形,且∠ACB为直角,
取AB的中点为D,由三角函数的最大值和最小值为1和﹣1,可得CD=1﹣(﹣1)=2
故AB的长度为2CD=4,又AB为函数的一个周期的长度,
故可得2,解之可得ω
故答案为.
本题考查三角函数的参数的意义,得出AB的两种表示方法是解决问题的关键,属中档题.
15.
设与之间的函数关系式为,根据表中数列可得周期和函数的最值,从而可求出,再利用最大值可求,故可求解析式.
【详解】
设与之间的函数关系式为,
则由表中数据可得,且,
故且,所以
因为当时,,所以,
解得,故,其中.
故答案为:.
16.
利用周期计算公式求出,由最高亮度距离平均亮度0.2星等可求出A,由平均亮度可求出b,即可写出三角函数模型.
【详解】
设所求函数为,由题意得,即,,,故.
故答案为:
本题考查模型在实际问题中的应用,属于基础题.
17.629
由题意得,代入正弦型函数的周期计算公式可求得,即可得解.
【详解】
由题意得,即,
∴,
∴正整数的最小值为629.
故答案为:629
本题考查正弦型函数的周期性,属于基础题.
18.(1);(2)每年的十一月初至第二年的四月末
(1)作出散点图,得到曲线后,根据周期变化特点可考虑用余弦型函数模型;结合图象可求得解析式;
(2)令可求得的取值,从而可确定最佳旅游时间.
【详解】
(1)以月份为横轴,气温为纵轴作出散点图,并以光滑的曲线连接各散点,得到如图所示的曲线
由于各地月平均气温是以个月为周期变化的,故依散点图所绘制的图象,可以考虑用来模拟
由最高气温为,最低气温为得:,
又
又时,y取最大值,则
为惠灵顿市的常年气温函数模型
(2)当时,或
说明在每年的十一月初至第二年的四月末气温不低于,是惠灵顿市的最佳旅游时间
本题考查三角函数的实际应用问题,关键是能够建立起合适的函数模型,进而通过三角函数图象求解析式的方法求得拟合的函数模型.
19.(1);(2).
(1)根据图象,结合三角函数的性质,得到和的值,再由最大值点,得出结果;
(2)根据题意,得到曲线的方程,求出的坐标,进而可求出四边形的面积.
【详解】
(1)由图象,可知,,
将代入中,
得,即.
∵,∴,故;
(2)在中,令,得,
从而得曲线的方程为,则,
∴矩形的面积为,即儿童乐园的面积为.
20.(1),;(2).
(1)由图可得,,,再由周期公式可求出,再把将,代入可求出的值,从而可求得函数的解析式;
(2)由可求出结果
【详解】
(1)由图可知,,.
∵,∴,解得,
∴.
将,代入上式,解得,,
∵,∴,
故该曲线的函数解析式为,.
(2)由题意得,即,解得,,即,.
∵,∴当时,即,
∴该海港在的轮船最佳进港时间总共为.
21.(1)图象见解析;(2)①3cm;②6cm;③1s.
(1)计算出周期为1,在一个周期内,结合“五点法”中五点及区间端点,列表描点连线作出图象;
(2)根据解析式作答.①令计算出即可;②即为函数的最大值;③即为函数的周期.
【详解】
解:(1)周期T==1(s).
列表:
t 0 1
2πt+ π 2π 2π+
3 6 0 -6 0 3
描点画图:
(2)①小球开始摆动(即t=0),离开平衡位置为3 cm.
②小球摆动时离开平衡位置的最大距离是6 cm.
③小球来回摆动一次需要1 s(即周期).
本题考查三角函数的应用,解题关键是正确认识函数式S=6sin.由解析式研究函数的性质、画出函数的图象.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.音叉是呈“Y”形的钢质或铝合金发声器(如图1),各种音叉可因其质量和叉臂长短、粗细不同而在振动时发出不同频率的纯音.敲击某个音叉时,在一定时间内,音叉上点P离开平衡位置的位移与时间的函数关系为.图2是该函数在一个周期内的图象,根据图中数据可确定的值为( )
A.200 B.400 C. D.
2.把函数的图像向右平移个单位长度,再把所得图像上所有点的横坐标扩大到原来的2倍,纵坐标不变,得到函数的图像.则函数的一个解析式为( )
A. B. C. D.
3.已知曲线C1:y=cos x,C2:y=sin (2x+),则下面结论正确的是
A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2
C.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2
D.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2
4.若将函数的图象向右平移个单位长度后为奇函数,则的值可以为( )
A. B. C. D.
5.已知简谐振动的振幅是,图象上相邻最高点和最低点的距离是5,且过点,则该简谐振动的频率和初相是( )
A., B.,
C., D.,
6.如图,某大楼AB旁有一山坡,其斜坡CD的坡度(或坡比),山坡坡面上点E处有一休息亭.某数学兴趣小组测得山坡坡脚C与大楼水平距离米,与休息亭距离米,并从E点测得大楼顶部点的仰角为,点A,B,C,D,E在同一平面内,则大楼AB的高度约为( )
(结果精确到0.1米;参考数据:,,)
A.89.0米 B.74.2米 C.74.0米 D.59.2米
7.为了得到函数的图象,可将的图象( )
A.向右平移个单位 B.向右平移个单位
C.向左平移个单位 D.向左平移个单位
8.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用.如图,一个半径为的筒车按逆时针方向每分钟转圈,筒车的轴心距离水面的高度为米.设筒车上的某个盛水筒到水面的距离为(单位:)(在水面下则为负数),若以盛水筒刚浮出水面时开始计算时间,则与时间(单位:)之间的关系为.则盛水筒出水后到达最高点的最少时间为( )
A. B. C. D.
9.已知函数的最小正周期为,将其图象向右平移个单位后得函数的图象,则函数的图象
A.关于直线对称 B.关于直线对称
C.关于点对称 D.关于点对称
10.若函数的图象向右平移个单位得到的图象对应的函数为,则下列说法正确的是( )
A.的图象关于对称 B.在上有2个零点
C.在区间上单调递减 D.在上的值域为
11.如图,一个摩天轮的半径为10m,轮子的最低处距离地面2m.如果此摩天轮按逆时针匀速转动,每30分钟转一圈,且当摩天轮上某人经过点(点与摩天轮天轮中心的高度相同)时开始计时,在摩天轮转动的一圈内,此人相对于地面的高度不小于17m的时间大约是( )
A.8分钟 B.10分钟 C.12分钟 D.14分钟
12.如图为一直径为m的水轮,水轮圆心距水面m,已知水轮每分钟转2圈,水轮上的点到水面的距离(m)与时间(s)满足关系是表示表示在水面下,则有( )
A. B.
C. D.
二、填空题
13.如图所示,一半径为4米的水轮,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动一圈,如果当水轮上点P从水中浮现时(图中点)开始计时,则点P第一次到达最高点需要___________秒.
14.函数y=sinωx(ω>0)的部分图象如图所示,点A,B是最高点,点C是最低点,若△ABC是直角三角形,则ω的值为____.
15.海水受日月的引カ,在一定的时候发生涨落的现象叫潮汐.一般早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋.下面是某港口在某季节某天的时间与水深值(单位:m)记录表.
时刻 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
水深值 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 5.0
试用一个三角函数来近似地描述这个港口的水深值y与时间的函数关系,则这个函数关系式是________.
16.某星星的亮度变化周期为10天,此星星的平均亮度为3.8星等,最高亮度距离平均亮度0.2星等,则可近似地描述此星星的亮度与时间之间关系的一个三角函数为________.
17.在电流强度与时间的关系中,要使t在任意的时间内电流强度I能取得最大值A与最小值,则正整数的最小值为________.
三、解答题
18.当我们所处的北半球为冬季的时候,新西兰的惠灵顿市恰好是盛夏,因此北半球的人们冬天愿意去那里旅游,下面是一份惠灵顿机场提供的月平均气温统计表.
(月份) 1 2 3 4 5 6 7 8 9 10 11 12
17.3 17.9 17.3 15.8 13.7 11.6 10.06 9.5 10.06 11.6 13.7 15.8
(1)根据这个统计表提供的数据,为惠灵顿市的月平均气温作出一个函数模型;
(2)当自然气温不低于13.7℃时,惠灵顿市最适宜旅游,试根据你所确定的函数模型,确定惠灵顿市的最佳旅游时间.
19.如图所示,莱蒙都会小区为美化环境,准备在小区内草坪的一侧修建一条直路OC,另一侧修建一条休闲大道.休闲大道的前一段OD是函数的图像的一部分,后一段DBC是函数,(,,,)的图像,图像的最高点为,且,垂足为点.
(1)求函数,(,,,)的解析式;
(2)若在草坪内修建如图所示的矩形儿童乐园 (阴影部分),点P在曲线OD上,其横坐标为,点在上,求儿童乐园的面积.
20.如图,某海港一天从的水位高度(单位:)随时间(单位:)的变化近似满足函数.
(1)求该函数的解析式;
(2)若该海港在水位高度不低于时为轮船最佳进港时间,那么该海港在,轮船最佳进港时间总共多少小时?
21.一根细线的一端固定,另一端悬挂一个小球,当小球来回摆动时,离开平衡位置的位移S(单位:cm)与时间t(单位:s)的函数关系是S=6sin.
(1)画出它的图象;
(2)回答以下问题:
①小球开始摆动(即t=0),离开平衡位置是多少?
②小球摆动时,离开平衡位置的最大距离是多少?
③小球来回摆动一次需要多少时间?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
根据函数图像,确定函数周期,从而可得的值.
【详解】
由图像可得,,,即,则.
故选:D.
本题主要考查三角函数的应用,考查正弦型函数的周期性,属于基础题型.
2.B
将函数的图像所有点的横坐标缩短到原来的,纵坐标不变,再向左平移个单位长度即得解.
【详解】
解:将函数的图像所有点的横坐标缩短到原来的,纵坐标不变,得到,再把函数的图象向左平移个单位长度,得到.
故选:B
3.D
【详解】
把C1上各点的横坐标缩短到原来的倍,纵坐标不变,得到函数y=cos2x图象,再把得到的曲线向左平移个单位长度,得到函数y=cos2(x+)=cos(2x+)=sin(2x+)的图象,即曲线C2,
故选D.
点睛:三角函数的图象变换,提倡“先平移,后伸缩”,但“先伸缩,后平移”也常出现在题目中,所以也必须熟练掌握.无论是哪种变形,切记每一个变换总是对字母而言. 函数是奇函数;函数是偶函数;函数是奇函数;函数是偶函数.
4.C
先由平移公式得出平移后的函数为,由该函数为奇函数可得答案.
【详解】
函数的图象向右平移个单位长度后可得
由题意为奇函数,则
所以,
对照分析答案,当时,
故选:C
5.C
根据正弦型函数的图象与性质求出振幅、周期,再由过点求出初相即可得解.
【详解】
由题意可知,A=,32+2=52,
则T=8,ω==,
y=sin.
由sin φ=,得sin φ=.
∵|φ|<,
∴φ=.
因此频率是,初相为.
故选:C
6.A
过点分别作底面,,然后根据题意分别求出,最后相加即可求出答案.
【详解】
如图,过点作底面垂线,于,
因为斜坡CD的坡度,所以
设,,在中,,即,
解得,则,
所以,
因为在E点测得大楼顶部点的仰角为,
所以
,
故选:A
7.A
将函数化为,根据图象平移变换可得结果.
【详解】
由题意得:
向右平移个单位即可得到的图象
故选:A.
该题考查的是三角函数的平移变换问题,关键是能够理解平移的量是自变量本身的变化量,属于基础题目.
8.D
由已知可得、、、的值,得到函数解析式,取求得的值即可.
【详解】
解:筒车按逆时针方向每分钟转1.5圈,,
则,振幅为筒车的半径,即,,
由题意,时,,,即,
,.
则,
由,得,,
,,得,.
当时,取最小值为.
故选:.
9.D
【详解】
由题意得,故,
∴,
∴,
∴,
∴.
∵,,
∴选项A,B不正确.
又,
,
∴选项C,不正确,选项D正确.选D.
10.B
求出的解析式,并整理后,根据正弦函数性质判断.
【详解】
由题意,
不是函数的最值,不是对称轴,A错;
由,,,其中是上的零点,B正确;
由得,,因此在是递减,在上递增,C错;
时,,,D错.
故选:B.
本题考查三角函数图象变换,考查三角函数的性质.掌握正弦函数性质是解题关键.
11.B
由题可得此人相对于地面的高度与时间的关系是,再令求出的范围即可得出.
【详解】
设时间为时,此人相对于地面的高度为,
则由题可得当时,,
在时间时,此人转过的角为,
此时此人相对于地面的高度,
令,则,
所以,解得,
故在摩天轮转动的一圈内,此人相对于地面的高度不小于17m的时间大约是.
故选:B.
本题考查三角函数的实际应用,解题的关键是得出高度与时间的关系,再解三角函数不等式即可.
12.A
根据题意可得出的值,以及该函数的最小正周期,利用周期公式可求得的值,进而得出结论.
【详解】
由题意可知为水轮的半径3,又水轮每分钟转2圈,故该函数的最小正周期为,所以.
故选:A.
本题考查三角函数解析式中参数的计算,考查计算能力,属于基础题.
13.20
根据题意,计算弧占圆周的比例即可得答案.
【详解】
如图,根据题意得,
所以在中,,
所以,故弧的长为三分之一的圆周长,
又因为水轮每60秒逆时针转动一圈,
所以当水轮上点P从水中浮现时(图中点P)开始计时,则点P第一次到达最高点需要20秒.
故答案为:20
14.
可得△ABC为等腰直角三角形,进而可得AB=2CD=4,还可得AB,解方程可得ω的值.
【详解】
解:由题意结合三角函数的对称性可知△ABC为等腰直角三角形,且∠ACB为直角,
取AB的中点为D,由三角函数的最大值和最小值为1和﹣1,可得CD=1﹣(﹣1)=2
故AB的长度为2CD=4,又AB为函数的一个周期的长度,
故可得2,解之可得ω
故答案为.
本题考查三角函数的参数的意义,得出AB的两种表示方法是解决问题的关键,属中档题.
15.
设与之间的函数关系式为,根据表中数列可得周期和函数的最值,从而可求出,再利用最大值可求,故可求解析式.
【详解】
设与之间的函数关系式为,
则由表中数据可得,且,
故且,所以
因为当时,,所以,
解得,故,其中.
故答案为:.
16.
利用周期计算公式求出,由最高亮度距离平均亮度0.2星等可求出A,由平均亮度可求出b,即可写出三角函数模型.
【详解】
设所求函数为,由题意得,即,,,故.
故答案为:
本题考查模型在实际问题中的应用,属于基础题.
17.629
由题意得,代入正弦型函数的周期计算公式可求得,即可得解.
【详解】
由题意得,即,
∴,
∴正整数的最小值为629.
故答案为:629
本题考查正弦型函数的周期性,属于基础题.
18.(1);(2)每年的十一月初至第二年的四月末
(1)作出散点图,得到曲线后,根据周期变化特点可考虑用余弦型函数模型;结合图象可求得解析式;
(2)令可求得的取值,从而可确定最佳旅游时间.
【详解】
(1)以月份为横轴,气温为纵轴作出散点图,并以光滑的曲线连接各散点,得到如图所示的曲线
由于各地月平均气温是以个月为周期变化的,故依散点图所绘制的图象,可以考虑用来模拟
由最高气温为,最低气温为得:,
又
又时,y取最大值,则
为惠灵顿市的常年气温函数模型
(2)当时,或
说明在每年的十一月初至第二年的四月末气温不低于,是惠灵顿市的最佳旅游时间
本题考查三角函数的实际应用问题,关键是能够建立起合适的函数模型,进而通过三角函数图象求解析式的方法求得拟合的函数模型.
19.(1);(2).
(1)根据图象,结合三角函数的性质,得到和的值,再由最大值点,得出结果;
(2)根据题意,得到曲线的方程,求出的坐标,进而可求出四边形的面积.
【详解】
(1)由图象,可知,,
将代入中,
得,即.
∵,∴,故;
(2)在中,令,得,
从而得曲线的方程为,则,
∴矩形的面积为,即儿童乐园的面积为.
20.(1),;(2).
(1)由图可得,,,再由周期公式可求出,再把将,代入可求出的值,从而可求得函数的解析式;
(2)由可求出结果
【详解】
(1)由图可知,,.
∵,∴,解得,
∴.
将,代入上式,解得,,
∵,∴,
故该曲线的函数解析式为,.
(2)由题意得,即,解得,,即,.
∵,∴当时,即,
∴该海港在的轮船最佳进港时间总共为.
21.(1)图象见解析;(2)①3cm;②6cm;③1s.
(1)计算出周期为1,在一个周期内,结合“五点法”中五点及区间端点,列表描点连线作出图象;
(2)根据解析式作答.①令计算出即可;②即为函数的最大值;③即为函数的周期.
【详解】
解:(1)周期T==1(s).
列表:
t 0 1
2πt+ π 2π 2π+
3 6 0 -6 0 3
描点画图:
(2)①小球开始摆动(即t=0),离开平衡位置为3 cm.
②小球摆动时离开平衡位置的最大距离是6 cm.
③小球来回摆动一次需要1 s(即周期).
本题考查三角函数的应用,解题关键是正确认识函数式S=6sin.由解析式研究函数的性质、画出函数的图象.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
