5.3导数在研究函数中的应用 同步练习(Word版含解析)
文档属性
| 名称 | 5.3导数在研究函数中的应用 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 991.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 00:00:00 | ||
图片预览




文档简介
人教A版(2019)选择性必修第二册 5.3导数在研究函数中的应用
一、单选题
1.函数的单调递减区间为( )
A. B.
C. D.
2.已知函数,,若,则的最小值为( )
A. B. C. D.
3.若不等式对于一切恒成立,则的最小值是( )
A.0 B. C. D.
4.函数在上的最大值与最小值分别为( )
A. B. C. D.
5.已知函数的导函数的图像如下,若在处有极值,则的值为( )
A. B. C. D.
6.若不等式对恒成立,则实数a的取值范围是( )
A. B. C. D.
7.若函数在区间上单调递增,则的取值范围是( )
A. B. C. D.
8.已知函数在上有两个零点,则a的取值范是( )
A. B.
C. D.
9.已知函数()有两个极值点 (),则的最大值为( )
A. B. C. D.
10.若函数在点处的切线方程为,则函数的增区间为( )
A. B. C. D.
11.设为实数,函数,且是偶函数,则的单调递增区间为( )
A. B.,
C. D.
12.函数在上的最小值为( )
A. B.-1 C.0 D.
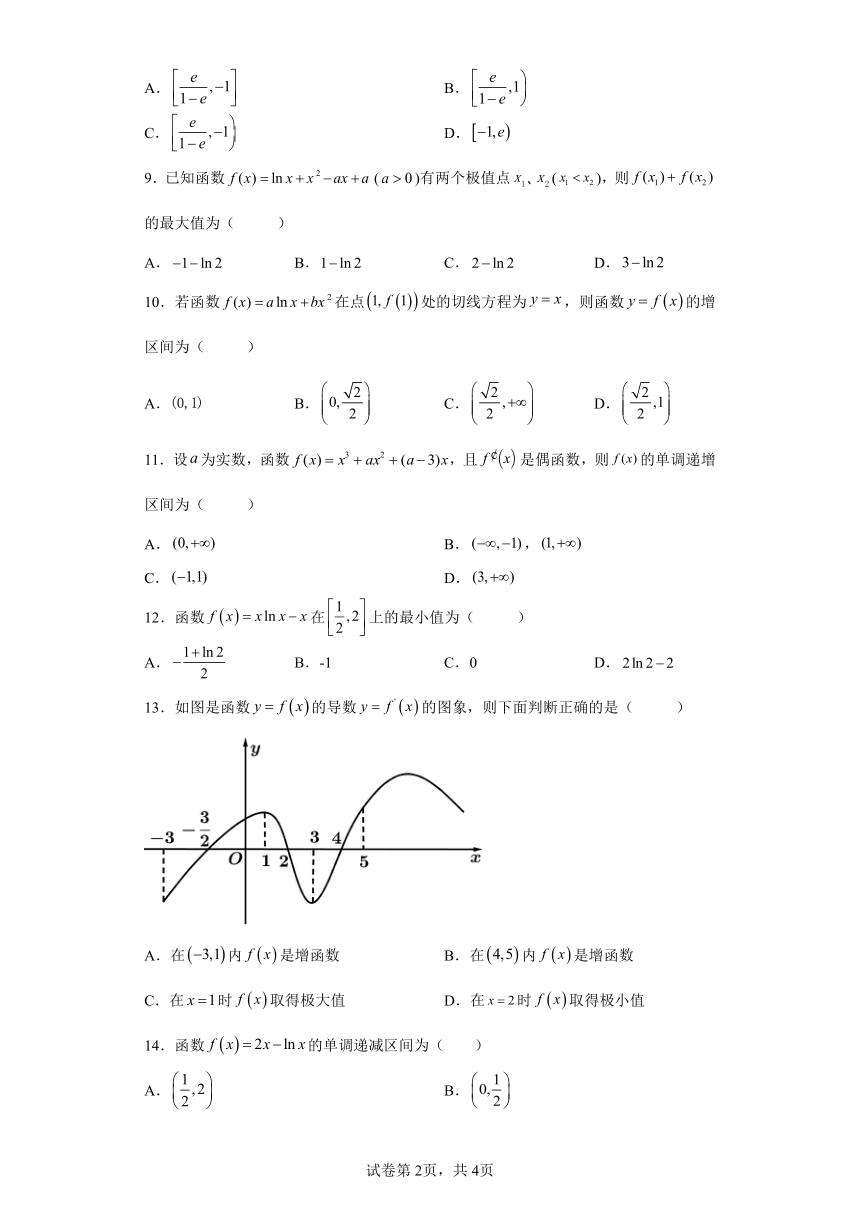
13.如图是函数的导数的图象,则下面判断正确的是( )
A.在内是增函数 B.在内是增函数
C.在时取得极大值 D.在时取得极小值
14.函数的单调递减区间为( )
A. B.
C. D.
15.音乐是用声音来表达思想情感的一种艺术,数学家傅里叶证明了所有的器乐和声乐的声音都可用简单正弦函数的和来描述,其中频率最低的称为基音,其余的称为泛音,而泛音的频率都是基音频率的整数倍,当一个发声体振动发声时,发声体是在全段振动的,除了频率最低的外,其余各部分(如二分之一 三分之一…)也在振动,所以我们听到声音的函数是,则声音函数的最大值是( )
A. B.1 C. D.
二、填空题
16.若函数在区间内不单调,则k的取值范围是__________.
17.已知函数,则函数的最小值为___________.
18.已知函数,对一切,恒成立,则的取值范围是________.
三、解答题
19.已知函数.
(1)若在区间上为增函数,求a的取值范围.
(2)若的单调递减区间为,求a的值.
20.已知函数().
(1)讨论的单调性;
(2)若函数有两个零点,求的取值范围.
21.在①的图象在点处的切线斜率为1;②;③有两个极值点-1,1这三个条件中任选一个补充在下面的问题(1)中,并加以解答.
已知.
(1)若______,求实数m的值;
注:如果选择多个条件分别解答,按第一个解答计分.
(2)若,讨论的单调性.
22.已知函数.
(1)求函数在的最大值;
(2)证明:函数在有两个极值点,并判断与的大小关系.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
先求导数,令求解不等式可得答案.
【详解】
由题可知,由,解得.
所以单调递减区间为.
故选:A.
2.D
令,得到关于t的函数式,进而可得关于t的函数式,构造函数利用导数研究单调性并确定最值,即可求的最小值.
【详解】
令,则,,
∴,,即,
若,则,
∴,有,
当时,,单调递减;当时,,单调递增;
∴,即的最小值为.
故选:D.
关键点点睛:令确定关于t的函数式,构造函数并利用导数求函数的最小值.
3.C
采用分离参数将问题转化为“对一切恒成立”,再利用基本不等式求解出的最小值,由此求解出的取值范围.
【详解】
因为不等式对于一切恒成立,
所以对一切恒成立,
所以,
又因为在上单调递减,所以,
所以,所以的最小值为,
故选:C.
本题考查利用基本不等式求解最值,涉及不等式在给定区间上的恒成立问题,难度一般.不等式在给定区间上恒成立求解参数范围的两种方法:参变分离法、分类讨论法.
4.A
利用导数法求解.
【详解】
解:因为函数,
所以,
令,得,
当或时,,当时,,
又,
所以在上的最大值与最小值分别为,
故选:A
5.B
根据极值与导数的关系判断.
【详解】
由知,时,,时,,时,,是极值点.虽然有,但在7的两侧,,7不是极值点.
故选:B.
6.C
由已知条件推导出,,令,利用导数求出函数的最小值,由此能求出实数的取值范围.
【详解】
解:对恒成立,
,,
令,
则,
当时,,当时,,
∴函数在上递减,在上递增,
所以
.
实数的取值范围是,.
故选:C.
7.B
由分离常数,利用构造函数法,结合导数,求得的取值范围.
【详解】
依题意在区间上恒成立,
即在区间上恒成立,
令,
,
在上递增,,
所以.
所以的取值范围是.
故选:B
8.C
根据解析式可得,原题转化为求在上有一个零点,当时,求导可得的单调性,分析不符合题意;当时,令,解得,分别讨论、和三种情况下的单调性,结合题意,即可求得a的范围.
【详解】
由题意得:,,
所以原题转化为求在上有一个零点,
,
当时,,则在上单调递减,且,不符合题意,
当时,令,解得,
当,即时,,此时在上单调递减,且,不符合题意,
当,即时,,此时在上单调递增,且,不符合题意,
当,即时,在上单调递增,在上单调递减,当时,在上有一个零点,
所以,解得,所以.
综上:a的取值范是
故选:C
解题的关键是当时,进行分段讨论,结合函数的单调性及零点的定义,分析求解,考查分析理解,分段讨论的思想,属中档题.
9.D
求得,设,根据题意,转化为在内有两个不等的实数根 ,利用二次函数的性质,求得,结合二次函数根与系数关系和二次函数的性质,即可求解.
【详解】
由题意,函数,可得函数的定义域为,
且,
设,
因为函数()有两个极值点 (),
即在内有两个不等的实数根 (),
可得,解得,
又因为 ,可得,
则
,当且仅当时,等号成立,
故的最大值为.
故选:D.
10.C
首先将代入得到切点为,求导得到,从而得到,解方程组得到,再利用导数求解单调区间即可.
【详解】
将代入得到,所以切点为.
因为,
所以,
所以,
当时,,为增函数.
所以函数的增区间为.
故选:C
11.B
先利用定义算出,在求导算出单调区间.
【详解】
因为,所以,
因为是偶函数,所以对恒成立,
即,即,
所以,所以,令,解得或,
所以的单调递增区间为,.
故选:B.
12.B
求导后求得函数的单调性,利用单调性求得函数的最小值.
【详解】
因为,所以在上单调递减,在上单调递增,所以.
故答案为:B.
13.B
根据图象判断的单调性,由此求得的极值点,进而确定正确选项.
【详解】
由图可知,在区间上递减;在区间上递增.
所以不是的极值点,是的极大值点.
所以ACD选项错误,B选项正确.
故选:B
14.B
利用导数法求解.
【详解】
因为,
所以,
当时,,
所以函数的单调递减区间为,
故选:B
15.C
首先确定函数的周期,接着在一个周期内函数的最大值即可.
【详解】
,周期为,
只需要求y在上最大值.
令,
解得:或或,
当时,,当时,,
当时,,当时,,
所以y在
时,;
时,y=0
.
故选:C.
16.
求解出,采用分类讨论的方法分析的单调性,从而求解出满足题意要求的的取值范围.
【详解】
因为,且,
当时,恒成立,所以在上单调递增,不符合;
当时,恒成立,所以在上单调递减,不符合;
当时,若,则,若,则,
所以在上单调递减,在上单调递增,符合题意,
综上可知:.
故答案为:.
本题考查利用导数研究函数的单调性,其中涉及到根据单调性求解参数范围,难度一般.本例中的“不单调”问题也可以先转化为“单调”问题,求出结果后再取其补集也能得到对应结果.
17.
利用导数判断函数的单调性,从而求函数的最值.
【详解】
因为,所以,
由,得,所以;
由,得,所以,
所以函数在上单调递减,在单调递增,
所以时函数有最小值,且函数的最小值为.
故答案为:.
18.
根据题意,通过分离参数法得出在上恒成立,再构造函数,利用导数研究函数的单调性和最值,求出,进而求得的取值范围.
【详解】
解:由题可知,,即,
得在上恒成立,
设,
则,
当时,,单调递减,
当时,,单调递增.
∴,
∴,
即的取值范围是.
故答案为:.
19.(1);(2)3.
(1)由题意可得在上恒成立,即在上恒成立,转化为不等式右边的最小值成立,可得答案;
(2)显然,否则函数在上递增.利用导数求出函数的递减区间为,再根据已知递减区间,可得答案
【详解】
(1)因为,且在区间上为增函数,
所以在上恒成立,即在(1,+∞)上恒成立,
所以在上恒成立,所以,即a的取值范围是
(2)由题意知.因为,所以.
由,得,
所以的单调递减区间为,
又已知的单调递减区间为,
所以,
所以,即.
本题考查了利用导数研究函数的单调性,特别要注意:函数在某个区间上递增或递减与函数的递增或递减区间是的区别,属于基础题.
20.(1)当时,在R上单调递增;当时,在上单调递减,在上单调递增;(2).
(1)对函数求导,进而讨论a的符号,进而得到函数的单调区间;
(2)由(1)可以判断,根据(1)可知,进而根据零点存在定理结合放缩法得到答案.
【详解】
(1)的定义域为R,,
①当时,恒成立,所以在R上单调递增;
②当时,令得,
当时,,单调递减,
当时,,单调递增,
所以在上单调递减,在上单调递增
综上所述,当时,在R上单调递增;当时,在上单调递减,在上单调递增.
(2)由(1)可知,时,在R上单调递增,函数至多有一个零点,不合题意.
时,在上单调递减,在上单调递增,因为函数有2个零点,所以,且.
记,则,所以时,,单调递减,所以,则,于是,则x<0时,.
所以当x<0时,,限定,则,
所以当且时,.
于是,若函数有2个零点,则.
在“,且”这一步之后,另一个特值不太好找,这时候需要利用得到,进而根据放缩法得到结论.
21.(1)答案见解析
(2)答案见解析
(1)易得,分别将三个条件代入即可计算出m;
(2)对m分,,三种情况讨论即可得到函数的单调性.
(1)
方案一:选条件①.
易得,
,.
方案二:选条件②.
易得,
,.
方案三:选条件③.
易得,
∴由,得,.
有两个极值点-1,1,,.
(2)
.
当时,由,得或.
(i)若,则.
在R上单调递增.
(ii)若,则.
∴当时,或;当时,.
在上单调递增,在上单调递减.
(iii)若,则.
∴当时,或;当时,.
在上单调递增,在上单调递减.
综上,当时,在上单调递增,在上单调递减;
当时,在R上单调递增;
当时,在上单调递增,在上单调递减.
22.(1);(2)证明见解析;.
(1)先求解出,然后再求解出,通过的取值正负判断出的单调性,再根据零点的存在性定理确定出的零点分布情况,由此确定出的单调性,结合所给区间即可求解出最大值;
(2)先求解出,然后将区间分成三段:、、,逐段分析的极值点并求解出极值点的范围,由此完成证明并判断出与的大小.
【详解】
解:(1)
当时,,则,故在上单调递增,
又,所以在有唯一的零点t.
当时,;当时,.
故在上单调递减,在上单调递增,
且,,所以在的最大值为.
(2),
①当时,均单调递增,所以单调递增,
又,
所以在有唯一的零点,
此时当时,;时,,
所以是极小值点,不妨让.
②当时,,单调递增,所以;
故在上单调递增,没有极值点;
③当,.由(1)知,在上单调递减,在上单调递增,
且,故有唯一的零点,
则时,,即单调递减;时,,即单调递增,
又,
所以在有唯一的零点,
此时时,;时,,
所以是极大值点,即,
所以在有两个极值点,其中,,
且,由于,所以.
因为,,且在上单调递减,
所以,即.
(判断极值点的时候,也对.)
思路点睛:利用导数求解函数最值的思路:
(1)若所给的闭区间不含参数,则只需对求导,并求在区间内的根,再计算使导数等于零的根的函数值,把该函数值与比较,其中最大的一个是最大值,最小的一个是最小值;
(2)若所给的区间含有参数,则需对求导,通过对参数分类讨论,判断函数的单调性,从而得到函数的最值.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.函数的单调递减区间为( )
A. B.
C. D.
2.已知函数,,若,则的最小值为( )
A. B. C. D.
3.若不等式对于一切恒成立,则的最小值是( )
A.0 B. C. D.
4.函数在上的最大值与最小值分别为( )
A. B. C. D.
5.已知函数的导函数的图像如下,若在处有极值,则的值为( )
A. B. C. D.
6.若不等式对恒成立,则实数a的取值范围是( )
A. B. C. D.
7.若函数在区间上单调递增,则的取值范围是( )
A. B. C. D.
8.已知函数在上有两个零点,则a的取值范是( )
A. B.
C. D.
9.已知函数()有两个极值点 (),则的最大值为( )
A. B. C. D.
10.若函数在点处的切线方程为,则函数的增区间为( )
A. B. C. D.
11.设为实数,函数,且是偶函数,则的单调递增区间为( )
A. B.,
C. D.
12.函数在上的最小值为( )
A. B.-1 C.0 D.
13.如图是函数的导数的图象,则下面判断正确的是( )
A.在内是增函数 B.在内是增函数
C.在时取得极大值 D.在时取得极小值
14.函数的单调递减区间为( )
A. B.
C. D.
15.音乐是用声音来表达思想情感的一种艺术,数学家傅里叶证明了所有的器乐和声乐的声音都可用简单正弦函数的和来描述,其中频率最低的称为基音,其余的称为泛音,而泛音的频率都是基音频率的整数倍,当一个发声体振动发声时,发声体是在全段振动的,除了频率最低的外,其余各部分(如二分之一 三分之一…)也在振动,所以我们听到声音的函数是,则声音函数的最大值是( )
A. B.1 C. D.
二、填空题
16.若函数在区间内不单调,则k的取值范围是__________.
17.已知函数,则函数的最小值为___________.
18.已知函数,对一切,恒成立,则的取值范围是________.
三、解答题
19.已知函数.
(1)若在区间上为增函数,求a的取值范围.
(2)若的单调递减区间为,求a的值.
20.已知函数().
(1)讨论的单调性;
(2)若函数有两个零点,求的取值范围.
21.在①的图象在点处的切线斜率为1;②;③有两个极值点-1,1这三个条件中任选一个补充在下面的问题(1)中,并加以解答.
已知.
(1)若______,求实数m的值;
注:如果选择多个条件分别解答,按第一个解答计分.
(2)若,讨论的单调性.
22.已知函数.
(1)求函数在的最大值;
(2)证明:函数在有两个极值点,并判断与的大小关系.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
先求导数,令求解不等式可得答案.
【详解】
由题可知,由,解得.
所以单调递减区间为.
故选:A.
2.D
令,得到关于t的函数式,进而可得关于t的函数式,构造函数利用导数研究单调性并确定最值,即可求的最小值.
【详解】
令,则,,
∴,,即,
若,则,
∴,有,
当时,,单调递减;当时,,单调递增;
∴,即的最小值为.
故选:D.
关键点点睛:令确定关于t的函数式,构造函数并利用导数求函数的最小值.
3.C
采用分离参数将问题转化为“对一切恒成立”,再利用基本不等式求解出的最小值,由此求解出的取值范围.
【详解】
因为不等式对于一切恒成立,
所以对一切恒成立,
所以,
又因为在上单调递减,所以,
所以,所以的最小值为,
故选:C.
本题考查利用基本不等式求解最值,涉及不等式在给定区间上的恒成立问题,难度一般.不等式在给定区间上恒成立求解参数范围的两种方法:参变分离法、分类讨论法.
4.A
利用导数法求解.
【详解】
解:因为函数,
所以,
令,得,
当或时,,当时,,
又,
所以在上的最大值与最小值分别为,
故选:A
5.B
根据极值与导数的关系判断.
【详解】
由知,时,,时,,时,,是极值点.虽然有,但在7的两侧,,7不是极值点.
故选:B.
6.C
由已知条件推导出,,令,利用导数求出函数的最小值,由此能求出实数的取值范围.
【详解】
解:对恒成立,
,,
令,
则,
当时,,当时,,
∴函数在上递减,在上递增,
所以
.
实数的取值范围是,.
故选:C.
7.B
由分离常数,利用构造函数法,结合导数,求得的取值范围.
【详解】
依题意在区间上恒成立,
即在区间上恒成立,
令,
,
在上递增,,
所以.
所以的取值范围是.
故选:B
8.C
根据解析式可得,原题转化为求在上有一个零点,当时,求导可得的单调性,分析不符合题意;当时,令,解得,分别讨论、和三种情况下的单调性,结合题意,即可求得a的范围.
【详解】
由题意得:,,
所以原题转化为求在上有一个零点,
,
当时,,则在上单调递减,且,不符合题意,
当时,令,解得,
当,即时,,此时在上单调递减,且,不符合题意,
当,即时,,此时在上单调递增,且,不符合题意,
当,即时,在上单调递增,在上单调递减,当时,在上有一个零点,
所以,解得,所以.
综上:a的取值范是
故选:C
解题的关键是当时,进行分段讨论,结合函数的单调性及零点的定义,分析求解,考查分析理解,分段讨论的思想,属中档题.
9.D
求得,设,根据题意,转化为在内有两个不等的实数根 ,利用二次函数的性质,求得,结合二次函数根与系数关系和二次函数的性质,即可求解.
【详解】
由题意,函数,可得函数的定义域为,
且,
设,
因为函数()有两个极值点 (),
即在内有两个不等的实数根 (),
可得,解得,
又因为 ,可得,
则
,当且仅当时,等号成立,
故的最大值为.
故选:D.
10.C
首先将代入得到切点为,求导得到,从而得到,解方程组得到,再利用导数求解单调区间即可.
【详解】
将代入得到,所以切点为.
因为,
所以,
所以,
当时,,为增函数.
所以函数的增区间为.
故选:C
11.B
先利用定义算出,在求导算出单调区间.
【详解】
因为,所以,
因为是偶函数,所以对恒成立,
即,即,
所以,所以,令,解得或,
所以的单调递增区间为,.
故选:B.
12.B
求导后求得函数的单调性,利用单调性求得函数的最小值.
【详解】
因为,所以在上单调递减,在上单调递增,所以.
故答案为:B.
13.B
根据图象判断的单调性,由此求得的极值点,进而确定正确选项.
【详解】
由图可知,在区间上递减;在区间上递增.
所以不是的极值点,是的极大值点.
所以ACD选项错误,B选项正确.
故选:B
14.B
利用导数法求解.
【详解】
因为,
所以,
当时,,
所以函数的单调递减区间为,
故选:B
15.C
首先确定函数的周期,接着在一个周期内函数的最大值即可.
【详解】
,周期为,
只需要求y在上最大值.
令,
解得:或或,
当时,,当时,,
当时,,当时,,
所以y在
时,;
时,y=0
.
故选:C.
16.
求解出,采用分类讨论的方法分析的单调性,从而求解出满足题意要求的的取值范围.
【详解】
因为,且,
当时,恒成立,所以在上单调递增,不符合;
当时,恒成立,所以在上单调递减,不符合;
当时,若,则,若,则,
所以在上单调递减,在上单调递增,符合题意,
综上可知:.
故答案为:.
本题考查利用导数研究函数的单调性,其中涉及到根据单调性求解参数范围,难度一般.本例中的“不单调”问题也可以先转化为“单调”问题,求出结果后再取其补集也能得到对应结果.
17.
利用导数判断函数的单调性,从而求函数的最值.
【详解】
因为,所以,
由,得,所以;
由,得,所以,
所以函数在上单调递减,在单调递增,
所以时函数有最小值,且函数的最小值为.
故答案为:.
18.
根据题意,通过分离参数法得出在上恒成立,再构造函数,利用导数研究函数的单调性和最值,求出,进而求得的取值范围.
【详解】
解:由题可知,,即,
得在上恒成立,
设,
则,
当时,,单调递减,
当时,,单调递增.
∴,
∴,
即的取值范围是.
故答案为:.
19.(1);(2)3.
(1)由题意可得在上恒成立,即在上恒成立,转化为不等式右边的最小值成立,可得答案;
(2)显然,否则函数在上递增.利用导数求出函数的递减区间为,再根据已知递减区间,可得答案
【详解】
(1)因为,且在区间上为增函数,
所以在上恒成立,即在(1,+∞)上恒成立,
所以在上恒成立,所以,即a的取值范围是
(2)由题意知.因为,所以.
由,得,
所以的单调递减区间为,
又已知的单调递减区间为,
所以,
所以,即.
本题考查了利用导数研究函数的单调性,特别要注意:函数在某个区间上递增或递减与函数的递增或递减区间是的区别,属于基础题.
20.(1)当时,在R上单调递增;当时,在上单调递减,在上单调递增;(2).
(1)对函数求导,进而讨论a的符号,进而得到函数的单调区间;
(2)由(1)可以判断,根据(1)可知,进而根据零点存在定理结合放缩法得到答案.
【详解】
(1)的定义域为R,,
①当时,恒成立,所以在R上单调递增;
②当时,令得,
当时,,单调递减,
当时,,单调递增,
所以在上单调递减,在上单调递增
综上所述,当时,在R上单调递增;当时,在上单调递减,在上单调递增.
(2)由(1)可知,时,在R上单调递增,函数至多有一个零点,不合题意.
时,在上单调递减,在上单调递增,因为函数有2个零点,所以,且.
记,则,所以时,,单调递减,所以,则,于是,则x<0时,.
所以当x<0时,,限定,则,
所以当且时,.
于是,若函数有2个零点,则.
在“,且”这一步之后,另一个特值不太好找,这时候需要利用得到,进而根据放缩法得到结论.
21.(1)答案见解析
(2)答案见解析
(1)易得,分别将三个条件代入即可计算出m;
(2)对m分,,三种情况讨论即可得到函数的单调性.
(1)
方案一:选条件①.
易得,
,.
方案二:选条件②.
易得,
,.
方案三:选条件③.
易得,
∴由,得,.
有两个极值点-1,1,,.
(2)
.
当时,由,得或.
(i)若,则.
在R上单调递增.
(ii)若,则.
∴当时,或;当时,.
在上单调递增,在上单调递减.
(iii)若,则.
∴当时,或;当时,.
在上单调递增,在上单调递减.
综上,当时,在上单调递增,在上单调递减;
当时,在R上单调递增;
当时,在上单调递增,在上单调递减.
22.(1);(2)证明见解析;.
(1)先求解出,然后再求解出,通过的取值正负判断出的单调性,再根据零点的存在性定理确定出的零点分布情况,由此确定出的单调性,结合所给区间即可求解出最大值;
(2)先求解出,然后将区间分成三段:、、,逐段分析的极值点并求解出极值点的范围,由此完成证明并判断出与的大小.
【详解】
解:(1)
当时,,则,故在上单调递增,
又,所以在有唯一的零点t.
当时,;当时,.
故在上单调递减,在上单调递增,
且,,所以在的最大值为.
(2),
①当时,均单调递增,所以单调递增,
又,
所以在有唯一的零点,
此时当时,;时,,
所以是极小值点,不妨让.
②当时,,单调递增,所以;
故在上单调递增,没有极值点;
③当,.由(1)知,在上单调递减,在上单调递增,
且,故有唯一的零点,
则时,,即单调递减;时,,即单调递增,
又,
所以在有唯一的零点,
此时时,;时,,
所以是极大值点,即,
所以在有两个极值点,其中,,
且,由于,所以.
因为,,且在上单调递减,
所以,即.
(判断极值点的时候,也对.)
思路点睛:利用导数求解函数最值的思路:
(1)若所给的闭区间不含参数,则只需对求导,并求在区间内的根,再计算使导数等于零的根的函数值,把该函数值与比较,其中最大的一个是最大值,最小的一个是最小值;
(2)若所给的区间含有参数,则需对求导,通过对参数分类讨论,判断函数的单调性,从而得到函数的最值.
答案第1页,共2页
答案第1页,共2页
