7.5正态分布 同步练习(Word版含解析)
文档属性
| 名称 | 7.5正态分布 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 592.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 05:12:58 | ||
图片预览




文档简介
人教A版(2019)选择性必修第三册 7.5 正态分布 同步练习
一、单选题
1.良好的睡眠是保证高中学生良好学习状态的基础,为了解某校高三学生的睡眠状况,该校调查了高三年级1200名学生的睡眠时间(单位:小时),经调查发现,这1200名学生每天的睡眠时间,则每天的睡眠时间为5~6小时的学生人数约为( )(结果四舍五入保留整数)
(附:若,则,,
A.163 B.51 C.26 D.20
2.某中学高三(1)班有50名学生,在一次高三模拟考试中,经统计得:数学成绩,则估计该班数学得分大于120分的学生人数为( )(参考数据:)
A.16 B.10 C.8 D.2
3.某电子管的正品率为,次品率为,现对该批电子管进行测试,那么在三次测试中恰有一次测到正品的概率是( )
A. B. C. D.
4.某综艺节目中,有一个盲拧魔方游戏,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方.为了解某市盲拧魔方爱好者的水平状况,某兴趣小组在全市范围内随机抽取了100名盲拧魔方爱好者进行调查,得到的情况如表所示:
用时/秒 [5,10] (10,15] (15,20] (20,25]
男性人数 15 22 14 9
女性人数 5 11 17 7
以这100名盲拧魔方爱好者用时不超过10秒的频率,代替全市所有盲拧魔方爱好者用时不超过10秒的概率,每位盲拧魔方爱好者用时是否超过10秒相互独立.若该兴趣小组在全市范围内再随机抽取20名盲拧魔方爱好者进行测试,其中用时不超过10秒的人数最有可能(即概率最大)是( )A.2 B.3 C.4 D.5
5.王老师为了了解全班50位同学某次考试的成绩状况,随机抽查了10位同学该次考试的数学与物理成绩,列表如下:
学生 甲 乙 丙 丁 戊 己 庚 辛 壬 癸 平均值 标准差
数学成绩X/分 88 62
物理成绩Y/分 75 63
若这10位同学的成绩能反映全班的成绩状况,且全班成绩服从正态分布,用实线表示全班数学成绩的正态曲线,虚线表示全班物理成绩的正态曲线,则随机变量与的正态曲线可能是( )A. B.
C. D.
6.若随机变量,且,则等于( )
A. B. C. D.
7.设随机变量ξ服从正态分布N(μ,σ2),ξ<1的概率是,则μ等于( )
A.1 B.2 C.4 D.不确定
8.已知,且,则( )
A.0.3 B.0.4 C.0.85 D.0.7
9.如图分别是甲、乙、丙三种品牌手表日走时误差分布的正态分布密度曲线,则下列说法不正确的是( )
A.三种品牌的手表日走时误差的均值相等
B.三种品牌的手表日走时误差的均值从大到小依次为甲、乙、丙
C.三种品牌的手表日走时误差的方差从小到大依次为甲、乙、丙
D.三种品牌手表中甲品牌的质量最好
10.已知随机变量,且,,则为( )
A.0.1358 B.0.1359 C.0.2716 D.0.2718
11.在某次学科知识竞赛中(总分100分),若参赛学生成绩服从(>0),若在(70,90)内的概率为0.7,则落在[90,100]内的概率为( )
A.0.2 B.0.15 C.0.1 D.0.05
12.某校团委决定举办“鉴史知来”读书活动,经过选拔,共10名同学的作品被选为优秀作品,其中高一年级5名同学,高二年级5名同学,现从这10个优秀作品中随机抽7个,则高二年级5名同学的作品全被抽出的概率为( )
A. B. C. D.
13.已知随机变量X,Y满足,且,则( )
A.2.4 B.3.4 C.4.2 D.4.4
14.设随机变量,函数没有零点的概率是0.5,则( )
附:若,则,.
A.0.1587 B.0.1359 C.0.2718 D.0.3413
15.已知随机变量服从正态分布,若,则( )
A. B. C. D.
二、填空题
16.已知随机变量,若,则______.
17.已知随机变量服从正态分布,若,则________.
18.红外线自动测温门能有效避免测温者与被测温者的近距离接触,降低潜在的病毒感染风险,为防控新冠肺炎,某厂生产的红外线自动测温门,其测量体温误差服从正态分布,从已经生产出的测温门中随机取出一件,则其测量体温误差在区间内的概率为___________.(附:若随机变量服从正态分布,则)
三、解答题
19.已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(I)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;
(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
20.某单位招考工作人员,须参加初试和复试,初试通过后组织考生参加复试,共5000人参加复试,复试共三道题,第一题考生答对得3分,答错得0分,后两题考生每答对一道题得5分,答错得0分,答完三道题后的得分之和为考生的复试成绩.
(1)通过分析可以认为考生初试成绩服从正态分布,其中,,试估计初试成绩不低于90分的人数;
(2)已知某考生已通过初试,他在复试中第一题答对的概率为,后两题答对的概率均为,且每道题回答正确与否互不影响.记该考生的复试试成绩为,求的分布列及数学期望.
附:若随机变量服从正态分布,则,,.
21.为了了解某类工程的工期,某公司随机选取了10个这类工程,得到如下数据(单位:天):17,23,19,21,22,21,19,17,22,19.
(1)若该类工程的工期服从正态分布,用样本的平均数和标准差分别作为和的估计值.
(ⅰ)求和的值;
(ⅱ)由于疫情需要,要求在22天之内完成一项此类工程,估计能够在规定时间内完成该工程的概率(精确到0.01).
(2)在上述10个这类工程的工期中任取2个工期,设这2个工期的差的绝对值为,求的分布列和数字期望.
附:若随机变量服从正态分布,则,,.
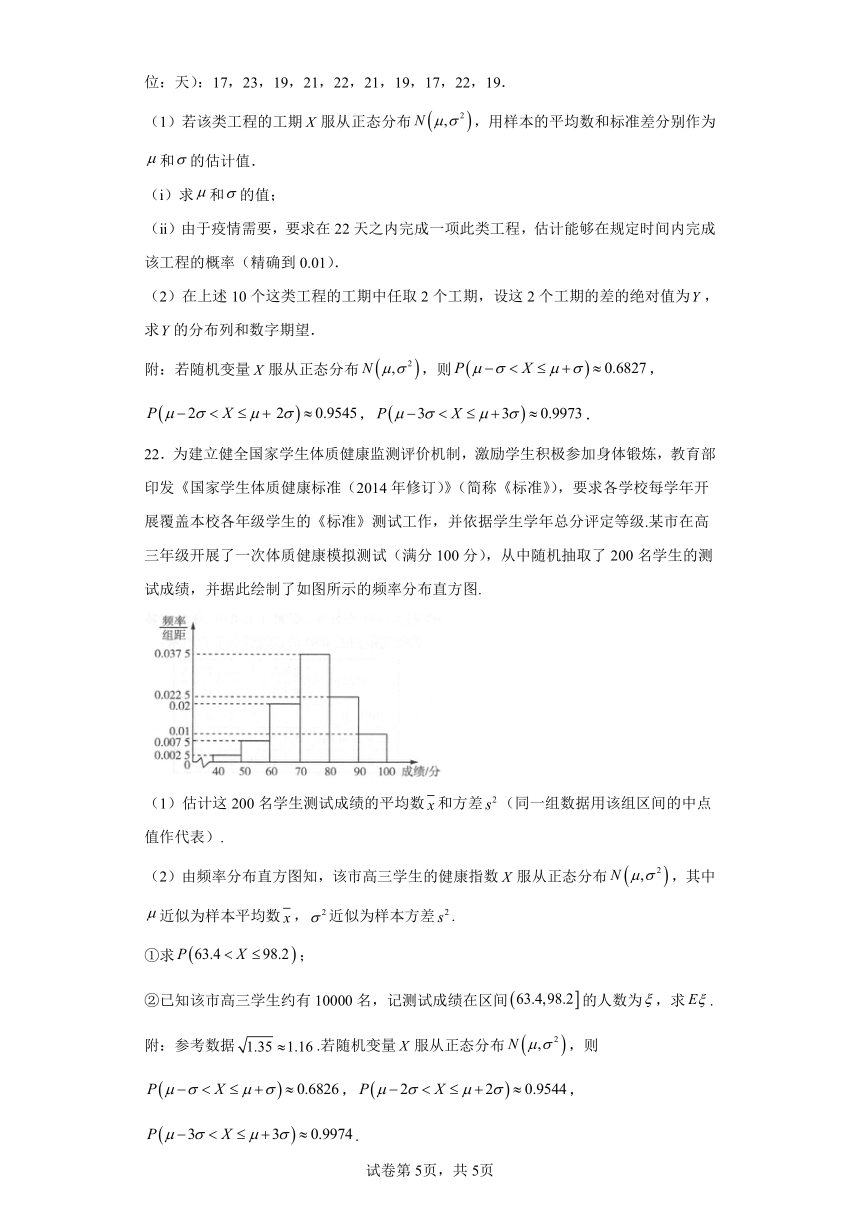
22.为建立健全国家学生体质健康监测评价机制,激励学生积极参加身体锻炼,教育部印发《国家学生体质健康标准(2014年修订)》(简称《标准》),要求各学校每学年开展覆盖本校各年级学生的《标准》测试工作,并依据学生学年总分评定等级.某市在高三年级开展了一次体质健康模拟测试(满分100分),从中随机抽取了200名学生的测试成绩,并据此绘制了如图所示的频率分布直方图.
(1)估计这200名学生测试成绩的平均数和方差(同一组数据用该组区间的中点值作代表).
(2)由频率分布直方图知,该市高三学生的健康指数服从正态分布,其中近似为样本平均数,近似为样本方差.
①求;
②已知该市高三学生约有10000名,记测试成绩在区间的人数为,求.
附:参考数据.若随机变量服从正态分布,则,,.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
由正态分布可知,,可确定,再结合正态分布曲线的对称性计算可求对应概率,结合频数=总数频率即可求解.
【详解】
解:由题意,,则,,所以
,,
则每天的睡眠时间为5~6小时的学生人数约为26.
故选:C.
2.C
根据正态分布的性质,结合题中所给的公式进行求解即可.
【详解】
因为数学成绩,所以,因此由
所以有,
估计该班数学得分大于120分的学生人数为,
故选:C
3.C
恰有一次测到正品,则有两次测到次品,再根据独立重复实验求概率得方法即可得解.
【详解】
解:由题意可知,三次测试中恰有一次测到正品,则有两次测到次品,故所求事件的概率为.
故选:C.
4.C
由条件求出1名盲拧魔方爱好者用时不超过10秒的概率为,设随机抽取的20名盲拧魔方爱好者中用时不超过10秒的人数为,则,由此可得,再由求其最大值,并确定对应的的值即可.
【详解】
根据题意得,1名盲拧魔方爱好者用时不超过10秒的概率为,设随机抽取的20名盲拧魔方爱好者中用时不超过10秒的人数为,
则,其中,,
当时,由,
得,化简得,
解得,又,∴,∴这20名盲拧魔方爱好者中用时不超过10秒的人数最有可能是4.
故选:C.
5.A
根据、的大小关系可得对称轴的位置关系,根据、可得图象的瘦高、矮胖,进而可得正确选项.
【详解】
因为,所以随机变量的正态曲线的对称轴在随机变量的正态曲线的对称轴的左边,排除B,C;
因为,所以随机变量的总体分布更离散,正态曲线比随机变量的正态曲线“矮胖”,排除D,
故选:A.
6.A
利用正态密度曲线的对称性可得出,即可得解.
【详解】
由于随机变量,则,
因此,.
故选:A.
7.A
利用正态分布图象的对称性,确定对称轴,即可知均值μ.
【详解】
由题意,ξ < 1的概率是,则ξ > 1的概率也是,
∴正态分布的图象关于对称,即.
故选:A
8.D
根据正态分布的性质计算可得;
【详解】
解:因为,正态曲线的对称轴为,因为,所以,所以
故选:D
9.B
观察图象可知图象的对称轴相同,所以其平均值相等,根据尖陡程度可以判断出其的大小关系,从而求得其结果.
【详解】
由题中图象可知三种品牌的手表日走时误差的平均数(均值)相等,
由正态密度曲线的性质,可知越大,正态曲线越扁平,越小,正态曲线越尖陡,
故三科总体的标准差从小到大依次为甲、乙、丙,
故选:B.
该题考查的是有关正态分布的问题,涉及到的知识点有根据概率密度曲线判断其均值和方差的特征,从而求得结果.
10.B
由随机变量可知,利用正态分布的对称性求解即可
【详解】
由随机变量知,,
所以,,
所以,
故选:B
11.B
由参赛学生成绩服从(>0),可知平均数,结合在概率密度曲线中的意义,即可计算得解.
【详解】
由参赛学生成绩服从(>0),
可知平均数,
则正态分布的概率密度曲线关于对称,
因为在(70,90)内的概率为0.7,
所以在内的概率为0.35,
所以在[90,100]内的概率为0.5-0.35=0.15.
故选:B.
本题考查了正态分布,考查了利用正态分布概率密度曲线的特征求概率,关键是理解平均数的含义,属于中档题.
12.A
用表示抽到高二年级同学的作品数,,即可得到答案.
【详解】
从10个作品中抽7个,用表示抽到高二年级同学的作品数,
则.
故选:A.
13.D
根据二项分布的知识求得,然后求得,从而求得正确答案.
【详解】
由题意,知随机变量X服从二项分布,,,
则,方差,又∵,∴,
∴,
∴.
故选:D
14.B
首先根据函数没有零点求出的取值范围,再根据没有零点的概率是,得到,再根据正态曲线的性质得到的值;然后再根据正态曲线的对称性求出的值即可.
【详解】
若函数没有零点,
∴二次方程无实根,
∴,∴.
又∵没有零点的概率是0.5,
∴.
由正态曲线的对称性知,
∴,∴,,
∴,,,,
∴,,
∴
.
故选:B.
15.B
利用正态密度曲线的对称性可得出,由此可求得结果.
【详解】
由于随机变量服从正态分布,则,
因此,.
故选:B.
本题考查利用正态密度曲线的对称性求概率,考查计算能力,属于基础题.
16.
根据随机变量服从正态分布,可知正态曲线的对称轴,利用对称性即可求出.
【详解】
因为,所以正态曲线的对称轴为,
因为,所以,
所以.
故答案为:
关键点点睛:本题的关键是充分利用正态曲线的对称性和曲线与轴之间的面积为1.
17.
根据正态分布曲线的对称性,得到,即可求解.
【详解】
由题意,随机变量服从正态分布,可得对称轴,则,
因为,
根据正态分布曲线的对称性,可得.
故答案为:.
18.
由题意可知,结合题意得出,,再由,即可得出答案.
【详解】
由红外线自动测温门测量体温误差服从正态分布,
得,.
测量体温误差在区间内的概率为:
.
故答案为:.
19.(Ⅰ)从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.(Ⅱ)(i)答案见解析;(ii).
【详解】
分析:(Ⅰ)由分层抽样的概念可知应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.
(Ⅱ)(i)随机变量X的所有可能取值为0,1,2,3.且分布列为超几何分布,即P(X=k)=(k=0,1,2,3).据此求解分布列即可,计算相应的数学期望为.
(ii)由题意结合题意和互斥事件概率公式可得事件A发生的概率为.
详解:(Ⅰ)由已知,甲、乙、丙三个部门的员工人数之比为3∶2∶2,
由于采用分层抽样的方法从中抽取7人,
因此应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.
(Ⅱ)(i)随机变量X的所有可能取值为0,1,2,3.
P(X=k)=(k=0,1,2,3).
所以,随机变量X的分布列为
X 0 1 2 3
P
随机变量X的数学期望.
(ii)设事件B为“抽取的3人中,睡眠充足的员工有1人,睡眠不足的员工有2人”;
事件C为“抽取的3人中,睡眠充足的员工有2人,睡眠不足的员工有1人”,
则A=B∪C,且B与C互斥,
由(i)知,P(B)=P(X=2),P(C)=P(X=1),
故P(A)=P(B∪C)=P(X=2)+P(X=1)=.
所以,事件A发生的概率为.
点睛:本题主要在考查超几何分布和分层抽样.超几何分布描述的是不放回抽样问题,随机变量为抽到的某类个体的个数.超几何分布的特征是:①考查对象分两类;②已知各类对象的个数;③从中抽取若干个个体,考查某类个体个数X的概率分布,超几何分布主要用于抽检产品、摸不同类别的小球等概率模型,其实质是古典概型.进行分层抽样的相关计算时,常利用以下关系式巧解:(1) ;(2)总体中某两层的个体数之比=样本中这两层抽取的个体数之比.
20.(1)114人;(2)分布列见解析,.
(1)通过分析得,,,初试成绩不低于90分的概率为求得人数;
(2)由题得的取值分别为0,3,5,8,10,13,分别计算对应概率列出分布列得解.
【详解】
(1)∵学生笔试成绩服从正态分布,其中,,
∴
∴估计笔试成绩不低于90分的人数为人
(2)的取值分别为0,3,5,8,10,13,
则
的分布为
故的分布列为:
0 3 5 8 10 13
利用正态曲线的对称性求概率是常见的正态分布应用问题.解题的关键是利用对称轴确定所求概率对应的随机变量的区间与已知概率对应的随机变量的区间的关系,必要时可借助图形判断.
对于正态分布,由是正态曲线的对称轴知:
(1)对任意的,有;
(2)
(3).
21.(1)(ⅰ),;(ⅱ)0.84;(2)分布列见解析,.
(1)(ⅰ)由公式计算平均数和标准差的值;(ⅱ)观察和与22的关系,由正态分布的知识得到所求概率.
(2)列出的所有可能取值,并求出每一个可能取值对应的概率,写出分布列,计算数学期望.
【详解】
解:(1)(ⅰ)样本的平均数为,
样本的标准差为.
因此,.
(ⅱ)22天之内完成该工程的概率
,
所以估计能够在规定时间内完成该工程的概率为0.84.
(2)把这10个工期从小到大排列,为17,17,19,19,19,21,21,22,22,23,则的可能取值为0,1,2,3,4,5,6,
,
,
,
,
,
,
.
所以的分布列是
0 1 2 3 4 5 6
的数学期望是
.
结论点睛:若,直线是正态曲线的对称轴:
(1);(2)对任意的实数,有①,②,③.
22.(1),;(2)①;②.
(1)根据平均数和方差的计算公式直接计算即可;
(2)①根据正态分布的概率直接计算可得;②可得,根据二项分布的期望公式即可求出.
【详解】
(1)由频率分布直方图可知,各区间对应的频数分布表如下:
成绩区间
频数 5 15 40 75 45 20
∴,
.
(2)①由(1)知服从正态分布,且,
∴.
②依题意,知,
则.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.良好的睡眠是保证高中学生良好学习状态的基础,为了解某校高三学生的睡眠状况,该校调查了高三年级1200名学生的睡眠时间(单位:小时),经调查发现,这1200名学生每天的睡眠时间,则每天的睡眠时间为5~6小时的学生人数约为( )(结果四舍五入保留整数)
(附:若,则,,
A.163 B.51 C.26 D.20
2.某中学高三(1)班有50名学生,在一次高三模拟考试中,经统计得:数学成绩,则估计该班数学得分大于120分的学生人数为( )(参考数据:)
A.16 B.10 C.8 D.2
3.某电子管的正品率为,次品率为,现对该批电子管进行测试,那么在三次测试中恰有一次测到正品的概率是( )
A. B. C. D.
4.某综艺节目中,有一个盲拧魔方游戏,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方.为了解某市盲拧魔方爱好者的水平状况,某兴趣小组在全市范围内随机抽取了100名盲拧魔方爱好者进行调查,得到的情况如表所示:
用时/秒 [5,10] (10,15] (15,20] (20,25]
男性人数 15 22 14 9
女性人数 5 11 17 7
以这100名盲拧魔方爱好者用时不超过10秒的频率,代替全市所有盲拧魔方爱好者用时不超过10秒的概率,每位盲拧魔方爱好者用时是否超过10秒相互独立.若该兴趣小组在全市范围内再随机抽取20名盲拧魔方爱好者进行测试,其中用时不超过10秒的人数最有可能(即概率最大)是( )A.2 B.3 C.4 D.5
5.王老师为了了解全班50位同学某次考试的成绩状况,随机抽查了10位同学该次考试的数学与物理成绩,列表如下:
学生 甲 乙 丙 丁 戊 己 庚 辛 壬 癸 平均值 标准差
数学成绩X/分 88 62
物理成绩Y/分 75 63
若这10位同学的成绩能反映全班的成绩状况,且全班成绩服从正态分布,用实线表示全班数学成绩的正态曲线,虚线表示全班物理成绩的正态曲线,则随机变量与的正态曲线可能是( )A. B.
C. D.
6.若随机变量,且,则等于( )
A. B. C. D.
7.设随机变量ξ服从正态分布N(μ,σ2),ξ<1的概率是,则μ等于( )
A.1 B.2 C.4 D.不确定
8.已知,且,则( )
A.0.3 B.0.4 C.0.85 D.0.7
9.如图分别是甲、乙、丙三种品牌手表日走时误差分布的正态分布密度曲线,则下列说法不正确的是( )
A.三种品牌的手表日走时误差的均值相等
B.三种品牌的手表日走时误差的均值从大到小依次为甲、乙、丙
C.三种品牌的手表日走时误差的方差从小到大依次为甲、乙、丙
D.三种品牌手表中甲品牌的质量最好
10.已知随机变量,且,,则为( )
A.0.1358 B.0.1359 C.0.2716 D.0.2718
11.在某次学科知识竞赛中(总分100分),若参赛学生成绩服从(>0),若在(70,90)内的概率为0.7,则落在[90,100]内的概率为( )
A.0.2 B.0.15 C.0.1 D.0.05
12.某校团委决定举办“鉴史知来”读书活动,经过选拔,共10名同学的作品被选为优秀作品,其中高一年级5名同学,高二年级5名同学,现从这10个优秀作品中随机抽7个,则高二年级5名同学的作品全被抽出的概率为( )
A. B. C. D.
13.已知随机变量X,Y满足,且,则( )
A.2.4 B.3.4 C.4.2 D.4.4
14.设随机变量,函数没有零点的概率是0.5,则( )
附:若,则,.
A.0.1587 B.0.1359 C.0.2718 D.0.3413
15.已知随机变量服从正态分布,若,则( )
A. B. C. D.
二、填空题
16.已知随机变量,若,则______.
17.已知随机变量服从正态分布,若,则________.
18.红外线自动测温门能有效避免测温者与被测温者的近距离接触,降低潜在的病毒感染风险,为防控新冠肺炎,某厂生产的红外线自动测温门,其测量体温误差服从正态分布,从已经生产出的测温门中随机取出一件,则其测量体温误差在区间内的概率为___________.(附:若随机变量服从正态分布,则)
三、解答题
19.已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(I)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;
(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
20.某单位招考工作人员,须参加初试和复试,初试通过后组织考生参加复试,共5000人参加复试,复试共三道题,第一题考生答对得3分,答错得0分,后两题考生每答对一道题得5分,答错得0分,答完三道题后的得分之和为考生的复试成绩.
(1)通过分析可以认为考生初试成绩服从正态分布,其中,,试估计初试成绩不低于90分的人数;
(2)已知某考生已通过初试,他在复试中第一题答对的概率为,后两题答对的概率均为,且每道题回答正确与否互不影响.记该考生的复试试成绩为,求的分布列及数学期望.
附:若随机变量服从正态分布,则,,.
21.为了了解某类工程的工期,某公司随机选取了10个这类工程,得到如下数据(单位:天):17,23,19,21,22,21,19,17,22,19.
(1)若该类工程的工期服从正态分布,用样本的平均数和标准差分别作为和的估计值.
(ⅰ)求和的值;
(ⅱ)由于疫情需要,要求在22天之内完成一项此类工程,估计能够在规定时间内完成该工程的概率(精确到0.01).
(2)在上述10个这类工程的工期中任取2个工期,设这2个工期的差的绝对值为,求的分布列和数字期望.
附:若随机变量服从正态分布,则,,.
22.为建立健全国家学生体质健康监测评价机制,激励学生积极参加身体锻炼,教育部印发《国家学生体质健康标准(2014年修订)》(简称《标准》),要求各学校每学年开展覆盖本校各年级学生的《标准》测试工作,并依据学生学年总分评定等级.某市在高三年级开展了一次体质健康模拟测试(满分100分),从中随机抽取了200名学生的测试成绩,并据此绘制了如图所示的频率分布直方图.
(1)估计这200名学生测试成绩的平均数和方差(同一组数据用该组区间的中点值作代表).
(2)由频率分布直方图知,该市高三学生的健康指数服从正态分布,其中近似为样本平均数,近似为样本方差.
①求;
②已知该市高三学生约有10000名,记测试成绩在区间的人数为,求.
附:参考数据.若随机变量服从正态分布,则,,.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
由正态分布可知,,可确定,再结合正态分布曲线的对称性计算可求对应概率,结合频数=总数频率即可求解.
【详解】
解:由题意,,则,,所以
,,
则每天的睡眠时间为5~6小时的学生人数约为26.
故选:C.
2.C
根据正态分布的性质,结合题中所给的公式进行求解即可.
【详解】
因为数学成绩,所以,因此由
所以有,
估计该班数学得分大于120分的学生人数为,
故选:C
3.C
恰有一次测到正品,则有两次测到次品,再根据独立重复实验求概率得方法即可得解.
【详解】
解:由题意可知,三次测试中恰有一次测到正品,则有两次测到次品,故所求事件的概率为.
故选:C.
4.C
由条件求出1名盲拧魔方爱好者用时不超过10秒的概率为,设随机抽取的20名盲拧魔方爱好者中用时不超过10秒的人数为,则,由此可得,再由求其最大值,并确定对应的的值即可.
【详解】
根据题意得,1名盲拧魔方爱好者用时不超过10秒的概率为,设随机抽取的20名盲拧魔方爱好者中用时不超过10秒的人数为,
则,其中,,
当时,由,
得,化简得,
解得,又,∴,∴这20名盲拧魔方爱好者中用时不超过10秒的人数最有可能是4.
故选:C.
5.A
根据、的大小关系可得对称轴的位置关系,根据、可得图象的瘦高、矮胖,进而可得正确选项.
【详解】
因为,所以随机变量的正态曲线的对称轴在随机变量的正态曲线的对称轴的左边,排除B,C;
因为,所以随机变量的总体分布更离散,正态曲线比随机变量的正态曲线“矮胖”,排除D,
故选:A.
6.A
利用正态密度曲线的对称性可得出,即可得解.
【详解】
由于随机变量,则,
因此,.
故选:A.
7.A
利用正态分布图象的对称性,确定对称轴,即可知均值μ.
【详解】
由题意,ξ < 1的概率是,则ξ > 1的概率也是,
∴正态分布的图象关于对称,即.
故选:A
8.D
根据正态分布的性质计算可得;
【详解】
解:因为,正态曲线的对称轴为,因为,所以,所以
故选:D
9.B
观察图象可知图象的对称轴相同,所以其平均值相等,根据尖陡程度可以判断出其的大小关系,从而求得其结果.
【详解】
由题中图象可知三种品牌的手表日走时误差的平均数(均值)相等,
由正态密度曲线的性质,可知越大,正态曲线越扁平,越小,正态曲线越尖陡,
故三科总体的标准差从小到大依次为甲、乙、丙,
故选:B.
该题考查的是有关正态分布的问题,涉及到的知识点有根据概率密度曲线判断其均值和方差的特征,从而求得结果.
10.B
由随机变量可知,利用正态分布的对称性求解即可
【详解】
由随机变量知,,
所以,,
所以,
故选:B
11.B
由参赛学生成绩服从(>0),可知平均数,结合在概率密度曲线中的意义,即可计算得解.
【详解】
由参赛学生成绩服从(>0),
可知平均数,
则正态分布的概率密度曲线关于对称,
因为在(70,90)内的概率为0.7,
所以在内的概率为0.35,
所以在[90,100]内的概率为0.5-0.35=0.15.
故选:B.
本题考查了正态分布,考查了利用正态分布概率密度曲线的特征求概率,关键是理解平均数的含义,属于中档题.
12.A
用表示抽到高二年级同学的作品数,,即可得到答案.
【详解】
从10个作品中抽7个,用表示抽到高二年级同学的作品数,
则.
故选:A.
13.D
根据二项分布的知识求得,然后求得,从而求得正确答案.
【详解】
由题意,知随机变量X服从二项分布,,,
则,方差,又∵,∴,
∴,
∴.
故选:D
14.B
首先根据函数没有零点求出的取值范围,再根据没有零点的概率是,得到,再根据正态曲线的性质得到的值;然后再根据正态曲线的对称性求出的值即可.
【详解】
若函数没有零点,
∴二次方程无实根,
∴,∴.
又∵没有零点的概率是0.5,
∴.
由正态曲线的对称性知,
∴,∴,,
∴,,,,
∴,,
∴
.
故选:B.
15.B
利用正态密度曲线的对称性可得出,由此可求得结果.
【详解】
由于随机变量服从正态分布,则,
因此,.
故选:B.
本题考查利用正态密度曲线的对称性求概率,考查计算能力,属于基础题.
16.
根据随机变量服从正态分布,可知正态曲线的对称轴,利用对称性即可求出.
【详解】
因为,所以正态曲线的对称轴为,
因为,所以,
所以.
故答案为:
关键点点睛:本题的关键是充分利用正态曲线的对称性和曲线与轴之间的面积为1.
17.
根据正态分布曲线的对称性,得到,即可求解.
【详解】
由题意,随机变量服从正态分布,可得对称轴,则,
因为,
根据正态分布曲线的对称性,可得.
故答案为:.
18.
由题意可知,结合题意得出,,再由,即可得出答案.
【详解】
由红外线自动测温门测量体温误差服从正态分布,
得,.
测量体温误差在区间内的概率为:
.
故答案为:.
19.(Ⅰ)从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.(Ⅱ)(i)答案见解析;(ii).
【详解】
分析:(Ⅰ)由分层抽样的概念可知应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.
(Ⅱ)(i)随机变量X的所有可能取值为0,1,2,3.且分布列为超几何分布,即P(X=k)=(k=0,1,2,3).据此求解分布列即可,计算相应的数学期望为.
(ii)由题意结合题意和互斥事件概率公式可得事件A发生的概率为.
详解:(Ⅰ)由已知,甲、乙、丙三个部门的员工人数之比为3∶2∶2,
由于采用分层抽样的方法从中抽取7人,
因此应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.
(Ⅱ)(i)随机变量X的所有可能取值为0,1,2,3.
P(X=k)=(k=0,1,2,3).
所以,随机变量X的分布列为
X 0 1 2 3
P
随机变量X的数学期望.
(ii)设事件B为“抽取的3人中,睡眠充足的员工有1人,睡眠不足的员工有2人”;
事件C为“抽取的3人中,睡眠充足的员工有2人,睡眠不足的员工有1人”,
则A=B∪C,且B与C互斥,
由(i)知,P(B)=P(X=2),P(C)=P(X=1),
故P(A)=P(B∪C)=P(X=2)+P(X=1)=.
所以,事件A发生的概率为.
点睛:本题主要在考查超几何分布和分层抽样.超几何分布描述的是不放回抽样问题,随机变量为抽到的某类个体的个数.超几何分布的特征是:①考查对象分两类;②已知各类对象的个数;③从中抽取若干个个体,考查某类个体个数X的概率分布,超几何分布主要用于抽检产品、摸不同类别的小球等概率模型,其实质是古典概型.进行分层抽样的相关计算时,常利用以下关系式巧解:(1) ;(2)总体中某两层的个体数之比=样本中这两层抽取的个体数之比.
20.(1)114人;(2)分布列见解析,.
(1)通过分析得,,,初试成绩不低于90分的概率为求得人数;
(2)由题得的取值分别为0,3,5,8,10,13,分别计算对应概率列出分布列得解.
【详解】
(1)∵学生笔试成绩服从正态分布,其中,,
∴
∴估计笔试成绩不低于90分的人数为人
(2)的取值分别为0,3,5,8,10,13,
则
的分布为
故的分布列为:
0 3 5 8 10 13
利用正态曲线的对称性求概率是常见的正态分布应用问题.解题的关键是利用对称轴确定所求概率对应的随机变量的区间与已知概率对应的随机变量的区间的关系,必要时可借助图形判断.
对于正态分布,由是正态曲线的对称轴知:
(1)对任意的,有;
(2)
(3).
21.(1)(ⅰ),;(ⅱ)0.84;(2)分布列见解析,.
(1)(ⅰ)由公式计算平均数和标准差的值;(ⅱ)观察和与22的关系,由正态分布的知识得到所求概率.
(2)列出的所有可能取值,并求出每一个可能取值对应的概率,写出分布列,计算数学期望.
【详解】
解:(1)(ⅰ)样本的平均数为,
样本的标准差为.
因此,.
(ⅱ)22天之内完成该工程的概率
,
所以估计能够在规定时间内完成该工程的概率为0.84.
(2)把这10个工期从小到大排列,为17,17,19,19,19,21,21,22,22,23,则的可能取值为0,1,2,3,4,5,6,
,
,
,
,
,
,
.
所以的分布列是
0 1 2 3 4 5 6
的数学期望是
.
结论点睛:若,直线是正态曲线的对称轴:
(1);(2)对任意的实数,有①,②,③.
22.(1),;(2)①;②.
(1)根据平均数和方差的计算公式直接计算即可;
(2)①根据正态分布的概率直接计算可得;②可得,根据二项分布的期望公式即可求出.
【详解】
(1)由频率分布直方图可知,各区间对应的频数分布表如下:
成绩区间
频数 5 15 40 75 45 20
∴,
.
(2)①由(1)知服从正态分布,且,
∴.
②依题意,知,
则.
答案第1页,共2页
答案第1页,共2页
