人教版A版(2019)课标高中数学必修二第六章平面向量及其应用6.4平面向量线性运算的应用 教案
文档属性
| 名称 | 人教版A版(2019)课标高中数学必修二第六章平面向量及其应用6.4平面向量线性运算的应用 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 102.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 19:55:18 | ||
图片预览


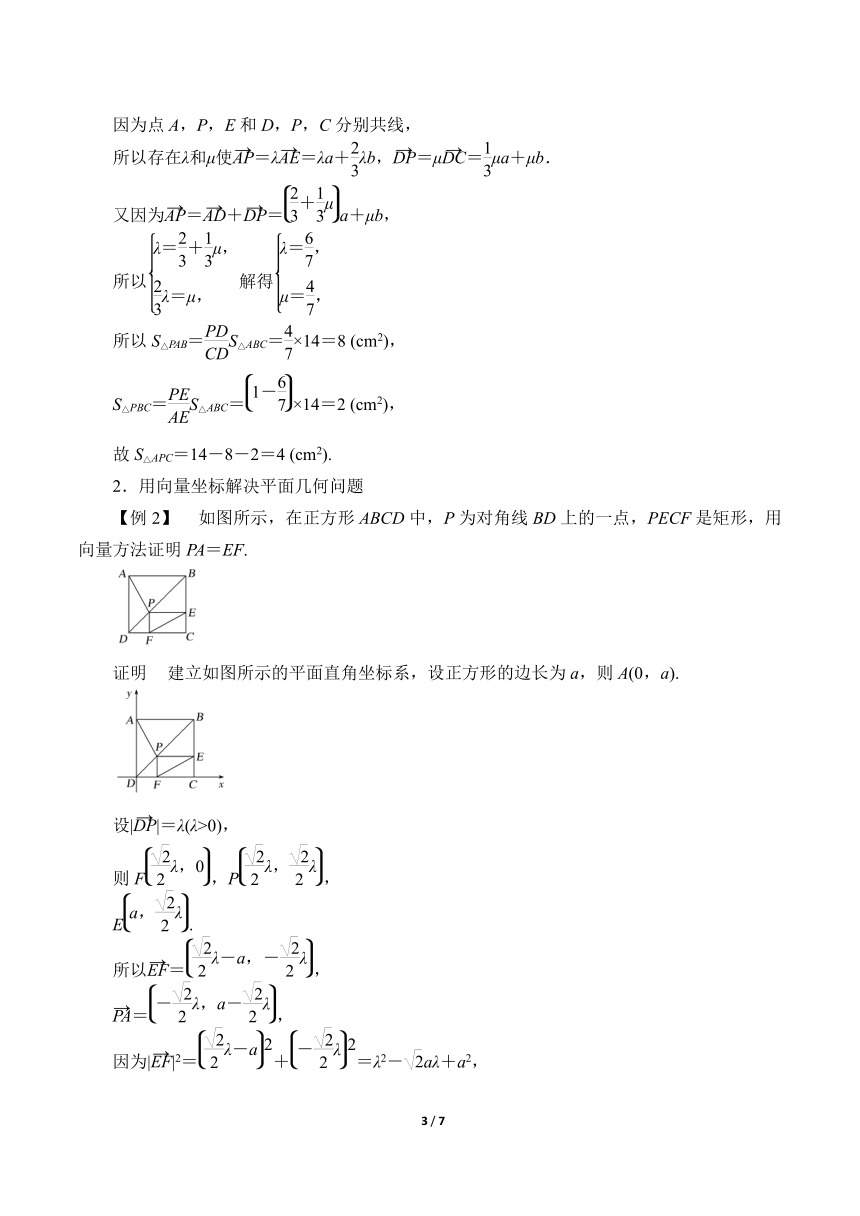
文档简介
平面向量线性运算的应用
【教学目标】
1.能用平面向量线性运算解决平面几何中的问题.
2.熟悉平面向量的线性运算在物理中的应用.
【教学重难点】
用平面向量线性运算解决平面几何中的问题.
【教学过程】
一、问题导入
如图所示,在细绳l上作用着一个大小为200 N,与水平方向的夹角为45°的力,细绳上挂着一个重物,使细绳的另一端与水平面平行.
问题1 水平方向OA上的拉力多大?
问题2 物重G是多少?
提示1 200×cos 45°=100(N),方向向右.
提示2 200×sin 45°=100(N).
二、新知探究
1.用向量解决平面几何问题
【例1】 如图所示,已知△ABC中,D,E,F分别是AC,AB,BC的中点,AF与CE相交于点O.
(1)求AO∶OF与CO∶OE的值;
(2)证明AF,BD,CE交于一点O.
(1)解 因为=+=+,
又因为E,F都是中点,所以
+=+=2+2=2.
另外,=+,所以+=2+2.
设=s,=t,
则有s-t=2+2,即
(s-2)=(t-2).
从而由共线向量基本定理可知s=t=2,
因此AO∶OF=CO∶OE=2∶1.
(2)证明 要证明AF,BD,CE交于一点O,只需证明B,O,D三点共线即可.
由(1)可知,=+,
=+=+=-
=-=(+),
又=(+),∴∥,又与有公共点B,
∴B,O,D三点共线,
故AF,BD,CE交于一点.
规律方法 利用向量线性运算解决几何问题的思路:
(1)把几何元素化为向量;
(2)进行向量的线性运算;
(3)把结果翻译成几何问题.
【训练1】 如图,已知△ABC的面积为14 cm2,D,E分别为AB,BC上的点,且AD∶DB=BE∶EC=2∶1,求△APC的面积.
解 设=a,=b为一组基底.
则=a+b,=a+b.
因为点A,P,E和D,P,C分别共线,
所以存在λ和μ使=λ=λa+λb,=μ=μa+μb.
又因为=+=a+μb,
所以解得
所以S△PAB=S△ABC=×14=8 (cm2),
S△PBC=S△ABC=×14=2 (cm2),
故S△APC=14-8-2=4 (cm2).
2.用向量坐标解决平面几何问题
【例2】 如图所示,在正方形ABCD中,P为对角线BD上的一点,PECF是矩形,用向量方法证明PA=EF.
证明 建立如图所示的平面直角坐标系,设正方形的边长为a,则A(0,a).
设||=λ(λ>0),
则F,P,
E.
所以=,
=,
因为||2=+=λ2-aλ+a2,
||2=+=λ2-aλ+a2,
所以||=||,即PA=EF.
规律方法 用坐标表示平面向量可将几何问题转化为代数问题,通过向量的坐标运算使问题得到解决,这是数形结合思想的重要体现.利用向量坐标法选取适当的位置建立坐标系是关键.
【训练2】 证明直角三角形ABC斜边AB上的中线CD等于斜边AB的一半.
证明 建立如图所示的平面直角坐标系.设C(0,0),A(a,0),B(0,b).
则AB=,中点D的坐标为,
即=,OD=||==,即CD=,故CD=AB.
3.平面向量在物理中的应用
【例3】 如图,用两根绳子把重10 N的物体W吊在水平杆AB上,∠ACW=150°,∠BCW=120°.求A和B处所受力的大小.(忽略绳子重量)
解 设A,B处所受力分别为f1,f2,10 N的重力用f表示,则f1+f2+f=0.
以重力作用点C为f1,f2的始点,作平行四边形CFWE,使CW为对角线,则=-f2,=-f1,=f.
∠ECW=180°-150°=30°,
∠FCW=180°-120°=60°,
∠FCE=90°,
∴四边形CEWF为矩形.
∴||=||cos 30°=5,
||=||cos 60°=5.
即A处所受力的大小为5 N,B处所受力的大小为5 N.
规律方法 由于力、位移、速度都是向量,对于解决力、位移、速度的大小、方向问题均可利用向量知识解决.
【训练3】 一辆汽车在平直公路上向西行驶,车上装着风速计和风向标,测得风向为东偏南30°,风速为4 m/s,这时气象台报告实际风速为2 m/s.试求风的实际方向和汽车的速度大小.
解 依据物理知识,有三个相对速度:汽车对地的速度为v车地,风对车的速度为v风车,风对地的速度为v风地,风对地的速度可以看成车对地与风对车的速度的合速度,即:v风地=v风车+v车地,如图,根据向量加法的平行四边形法则,可知表示向量v风地的有向线段是 ACDB的对角线.因为||=4 m,∠ACD=30°,
||=2,
所以∠ADC=90°,在Rt△ADC中,
||=||·cos 30°=2(m/s).
所以风的实际方向是吹向正南方向;汽车速度的大小为2 m/s.
三、课堂小结
1.通过学习平面向量线性运算的应用,培养运算、分析和解决实际问题的能力,提升直观想象、数学运算和逻辑推理素养.
2.对于解决平面几何问题,首先要结合图形的特点,确定能否建立平面直角坐标系是关键.
3.力、速度、加速度、位移的合成与分解就是向量的加、减运算,运动的叠加也用到向量的合成.
四、课堂检测
1.已知作用在点A的三个力f1=(3,4),f2=(2,-5),f3=(3,1),且A(1,1),则合力f=f1+f2+f3的终点坐标为( )
A.(9,1) B.(1,9)
C.(9,0) D.(0,9)
解析 f=f1+f2+f3=(3,4)+(2,-5)+(3,1)=(8,0),
设合力f的终点为P(x,y),则
=+f=(1,1)+(8,0)=(9,1).
答案 A
2.设点M是线段BC的中点,点A在直线BC外,且||2=16,|+|=|-|,则||=( )
A.8 B.4
C.2 D.1
解析 由||2=16,得||=4,
|+|=|-|=||=4,
而|+|=2||,故||=2,故选C.
答案 C
3.若=(2,2),=(-2,3)分别表示力F1,F2,则|F1+F2|为________.
解析 ∵F1+F2=(0,5),∴|F1+F2|==5.
答案 5
4.如图,已知点O是平行四边形ABCD的中心,E,F分别在边CD,AB上,且==.
求证:点E,O,F在同一直线上.
证明 设=m,=n,由==,
知E,F分别是CD,AB的三等分点,
∴=+=+
=-m+(m+n)=m+n,
=+=+=(m+n)-m
=m+n.∴=.
又O为和的公共点,故点E,O,F在同一直线上.
1 / 7
【教学目标】
1.能用平面向量线性运算解决平面几何中的问题.
2.熟悉平面向量的线性运算在物理中的应用.
【教学重难点】
用平面向量线性运算解决平面几何中的问题.
【教学过程】
一、问题导入
如图所示,在细绳l上作用着一个大小为200 N,与水平方向的夹角为45°的力,细绳上挂着一个重物,使细绳的另一端与水平面平行.
问题1 水平方向OA上的拉力多大?
问题2 物重G是多少?
提示1 200×cos 45°=100(N),方向向右.
提示2 200×sin 45°=100(N).
二、新知探究
1.用向量解决平面几何问题
【例1】 如图所示,已知△ABC中,D,E,F分别是AC,AB,BC的中点,AF与CE相交于点O.
(1)求AO∶OF与CO∶OE的值;
(2)证明AF,BD,CE交于一点O.
(1)解 因为=+=+,
又因为E,F都是中点,所以
+=+=2+2=2.
另外,=+,所以+=2+2.
设=s,=t,
则有s-t=2+2,即
(s-2)=(t-2).
从而由共线向量基本定理可知s=t=2,
因此AO∶OF=CO∶OE=2∶1.
(2)证明 要证明AF,BD,CE交于一点O,只需证明B,O,D三点共线即可.
由(1)可知,=+,
=+=+=-
=-=(+),
又=(+),∴∥,又与有公共点B,
∴B,O,D三点共线,
故AF,BD,CE交于一点.
规律方法 利用向量线性运算解决几何问题的思路:
(1)把几何元素化为向量;
(2)进行向量的线性运算;
(3)把结果翻译成几何问题.
【训练1】 如图,已知△ABC的面积为14 cm2,D,E分别为AB,BC上的点,且AD∶DB=BE∶EC=2∶1,求△APC的面积.
解 设=a,=b为一组基底.
则=a+b,=a+b.
因为点A,P,E和D,P,C分别共线,
所以存在λ和μ使=λ=λa+λb,=μ=μa+μb.
又因为=+=a+μb,
所以解得
所以S△PAB=S△ABC=×14=8 (cm2),
S△PBC=S△ABC=×14=2 (cm2),
故S△APC=14-8-2=4 (cm2).
2.用向量坐标解决平面几何问题
【例2】 如图所示,在正方形ABCD中,P为对角线BD上的一点,PECF是矩形,用向量方法证明PA=EF.
证明 建立如图所示的平面直角坐标系,设正方形的边长为a,则A(0,a).
设||=λ(λ>0),
则F,P,
E.
所以=,
=,
因为||2=+=λ2-aλ+a2,
||2=+=λ2-aλ+a2,
所以||=||,即PA=EF.
规律方法 用坐标表示平面向量可将几何问题转化为代数问题,通过向量的坐标运算使问题得到解决,这是数形结合思想的重要体现.利用向量坐标法选取适当的位置建立坐标系是关键.
【训练2】 证明直角三角形ABC斜边AB上的中线CD等于斜边AB的一半.
证明 建立如图所示的平面直角坐标系.设C(0,0),A(a,0),B(0,b).
则AB=,中点D的坐标为,
即=,OD=||==,即CD=,故CD=AB.
3.平面向量在物理中的应用
【例3】 如图,用两根绳子把重10 N的物体W吊在水平杆AB上,∠ACW=150°,∠BCW=120°.求A和B处所受力的大小.(忽略绳子重量)
解 设A,B处所受力分别为f1,f2,10 N的重力用f表示,则f1+f2+f=0.
以重力作用点C为f1,f2的始点,作平行四边形CFWE,使CW为对角线,则=-f2,=-f1,=f.
∠ECW=180°-150°=30°,
∠FCW=180°-120°=60°,
∠FCE=90°,
∴四边形CEWF为矩形.
∴||=||cos 30°=5,
||=||cos 60°=5.
即A处所受力的大小为5 N,B处所受力的大小为5 N.
规律方法 由于力、位移、速度都是向量,对于解决力、位移、速度的大小、方向问题均可利用向量知识解决.
【训练3】 一辆汽车在平直公路上向西行驶,车上装着风速计和风向标,测得风向为东偏南30°,风速为4 m/s,这时气象台报告实际风速为2 m/s.试求风的实际方向和汽车的速度大小.
解 依据物理知识,有三个相对速度:汽车对地的速度为v车地,风对车的速度为v风车,风对地的速度为v风地,风对地的速度可以看成车对地与风对车的速度的合速度,即:v风地=v风车+v车地,如图,根据向量加法的平行四边形法则,可知表示向量v风地的有向线段是 ACDB的对角线.因为||=4 m,∠ACD=30°,
||=2,
所以∠ADC=90°,在Rt△ADC中,
||=||·cos 30°=2(m/s).
所以风的实际方向是吹向正南方向;汽车速度的大小为2 m/s.
三、课堂小结
1.通过学习平面向量线性运算的应用,培养运算、分析和解决实际问题的能力,提升直观想象、数学运算和逻辑推理素养.
2.对于解决平面几何问题,首先要结合图形的特点,确定能否建立平面直角坐标系是关键.
3.力、速度、加速度、位移的合成与分解就是向量的加、减运算,运动的叠加也用到向量的合成.
四、课堂检测
1.已知作用在点A的三个力f1=(3,4),f2=(2,-5),f3=(3,1),且A(1,1),则合力f=f1+f2+f3的终点坐标为( )
A.(9,1) B.(1,9)
C.(9,0) D.(0,9)
解析 f=f1+f2+f3=(3,4)+(2,-5)+(3,1)=(8,0),
设合力f的终点为P(x,y),则
=+f=(1,1)+(8,0)=(9,1).
答案 A
2.设点M是线段BC的中点,点A在直线BC外,且||2=16,|+|=|-|,则||=( )
A.8 B.4
C.2 D.1
解析 由||2=16,得||=4,
|+|=|-|=||=4,
而|+|=2||,故||=2,故选C.
答案 C
3.若=(2,2),=(-2,3)分别表示力F1,F2,则|F1+F2|为________.
解析 ∵F1+F2=(0,5),∴|F1+F2|==5.
答案 5
4.如图,已知点O是平行四边形ABCD的中心,E,F分别在边CD,AB上,且==.
求证:点E,O,F在同一直线上.
证明 设=m,=n,由==,
知E,F分别是CD,AB的三等分点,
∴=+=+
=-m+(m+n)=m+n,
=+=+=(m+n)-m
=m+n.∴=.
又O为和的公共点,故点E,O,F在同一直线上.
1 / 7
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
