第四章 三角形 单元测试题（含答案）

中小学教育资源及组卷应用平台
七年级数学《三角形》单元测试题
姓名 学号 得分
一.选择题(每题3分，共30分)
1．以下面各组线段为边，能组成三角形的是（ ）．
A．1cm，2cm，4cm B．8cm，6cm，4cm
C．12cm，5cm，6cm D．2cm，3cm，6cm
如图，D是△ABC中AC边上一点，E是BD上的一点，
则对∠A，∠1，∠2之间关系描述正确的是（ ）．
（A）∠A<∠1<∠2 （B）∠2>∠1>∠A （C）∠1>∠2>∠A （D）无法判断
3．下列说法错误的是（ ）．
A．锐角三角形的三条高线，三条中线，三条角平分线分别交于一点
B．钝角三角形有两条高线在三角形外部
C．直角三角形只有一条高线
D．任意三角形都有三条高线，三条中线，三条角平分线
4．某人到瓷砖店去购买一种多边形形状的瓷砖，用来铺设无缝地板，他购买的瓷砖形状不可以是（ ）．
A．正三角形 B．长方形 C．正八边形 D．正六边形
5．如图，共有三角形的个数是（ ）
A．3 B．4 C．5 D．6
把一个多边形截去一个内角后,它的内角和为12600,
则原来这个多边形的边数不可能为( )
A．8 B.9 C．10 D．11
如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么与这个外角 相邻的内角的度数为( )
A.30° B.60° C.90° D.120°
8.如图所示，某同学把一块三角形玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（ ）
A.带①去 B. 带②去 C. 带③去 D. 带①和②去
9.如图，已知AB∥CD，AD∥BC，那么图中共有全等三角形（ ）
A．4对 B．2对 C．1对 D．不能确定
10.如图20所示，∠A+∠B+∠C+∠D+∠E=（ ）
A.180° B.260° C.270° D.360°
第10题图
二.填空题(每题4分，共28分)
11.要使五边形木架不变形，则至少要钉上_______根木条．
12.一个多边形的每一个外角都等于30°，这个多边形的边数是 ，它的内角和是 。
13.等腰三角形的周长为20cm，一边长为6cm，则其余两边长为______．
14.如图所示,∠A=50°,∠B=40°,∠C=30°,则∠BDC=________
15．已知等腰三角形ABC中,AB=AC=10cm,D为AC边上一点,且BD=AD,△BCD的周长为15cm,则底边BC的长为__________.
16.如图，三角形纸片ABC中，∠A＝65°，∠B＝75°，将纸片的一角折叠，使点C落在△ABC内，若∠1＝20°，则∠2的度数为______．
(
（1
6
题）
)
（第14题） （第17题 ）
17.如图5所示，在△ABC和△DCB中，AB=DC，要使△ABO≌△DCO，请你补充条件________________(只填写一个你认为合适的条件)。
三.简答题（每小题6分，共18分）
18.在△ABC中：画出BC边上的高AD、中线AE和∠B的平分线BF。
19.在△ABC中，AB=AC,AC上的中线BD把△ABC的周长分为24和18两部分,
求△ABC三边的长。
20.在△ABC中,已知∠B-∠A=5°,∠C-∠B=20°,求三角形各内角的度数。
四、解答题（每小题8分，共24分）
21.如图，A、D、F、B在同一直线上，已知AD ＝ BF，∠EFA＝60°，AE∥BC，且AE ＝ BC，
下面是求∠CDB的过程，请补充完整。　　
解： ∵ AD ＝ BF（已知）
∴ AD＋DF＝BF＋DF（ ）
即 AF ＝BD
又 ∵__________ （已知）
∴ ∠A＝∠B （ ）
在△AEF与△BCD中， ∴ △AEF ≌△BCD （ ）
AE ＝BC（已知） ∴∠CDB ＝_________
∠A＝∠B （已求） （ ）
_______＝ ________ 又 ∵ ∠EFA＝ 60°
∴ ∠CDB ＝ 60°
22.如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,
求∠DAC的度数。
23.如图9所示，在△ABC中，D是BC上一点且AB＝AC＝BD，∠1＝30°，你能求出△ABC各内角的度数吗？若能，写出求解过程；若不能，请说明理由。
五、解答题（每小题10分，共20分）
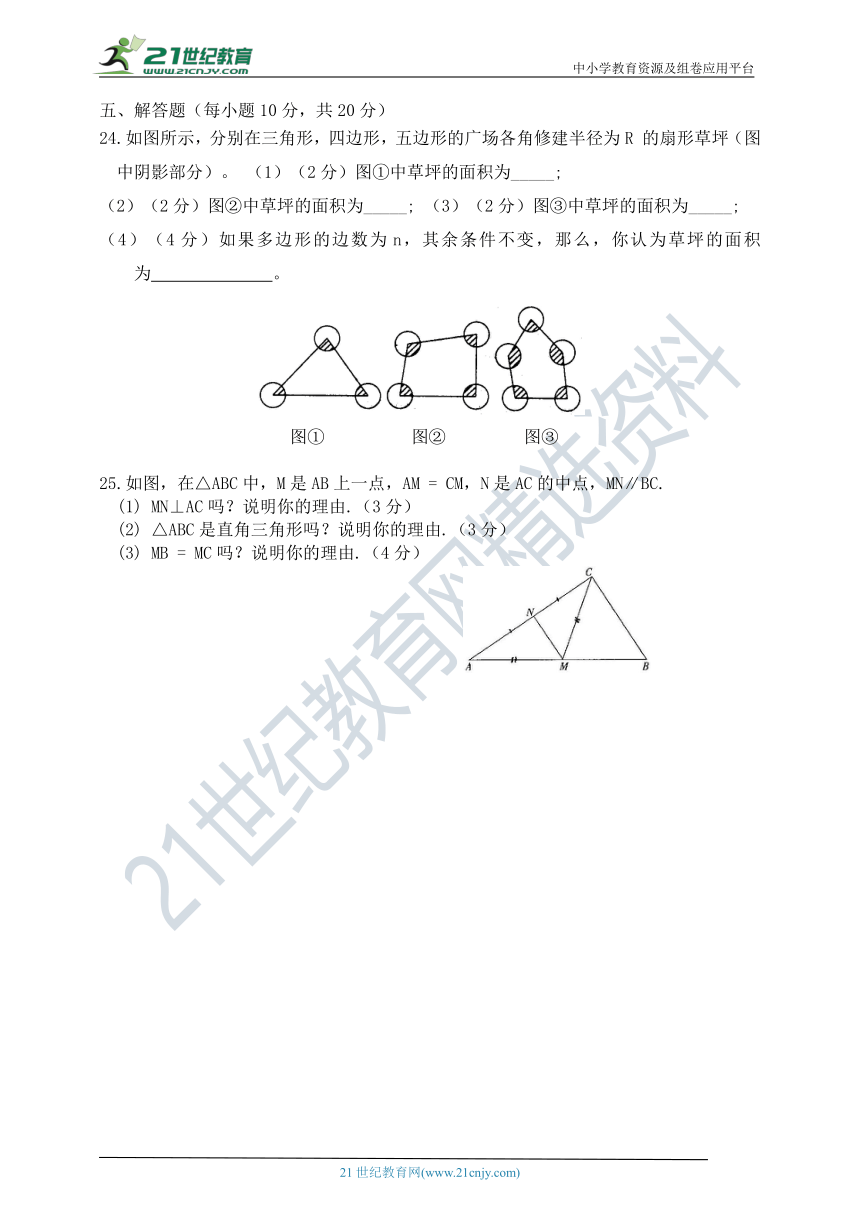
24.如图所示，分别在三角形，四边形，五边形的广场各角修建半径为R的扇形草坪（图中阴影部分）。 （1）（2分）图①中草坪的面积为_____;
（2）（2分）图②中草坪的面积为_____; （3）（2分）图③中草坪的面积为_____;
（4）（4分）如果多边形的边数为n，其余条件不变，那么，你认为草坪的面积为 。
图① 图② 图③
25.如图，在△ABC中，M是AB上一点，AM = CM，N是AC的中点，MN∥BC.
(1) MN⊥AC吗？说明你的理由.（3分）
(2) △ABC是直角三角形吗？说明你的理由.（3分）
(3) MB = MC吗？说明你的理由.（4分）
参考答案：
BACCD DCCAA
11、2; 12、12,1800°； 13、6cm,8cm或7cm,7cm; 14、120°； 15、5cm;
16、60°；17、∠A=∠D或∠ABO=∠DCO或∠ABC=∠DCB (答案不唯一）。
三、18、（作图略） A
解：分两种情况： 2x x
如图：当AB+AD=24时， D
设AD=CD=x,则AB=2x
有2x+x=24，解得x=8.
所以，AB=AC=2x=16, B C
BC=(24+18)-16×2=10.
当AB+AD=18 时，
有2x+x=18，解得x=6.所以，AB=AC=2x=12,
BC=(24+18)-12×2=18.
综上，△ABC三边的长为 AB=AC=16,BC=10：或AB=AC=12,BC=18.
解：因为∠B-∠A=5°,∠C-∠B=20°
所以∠B=∠A+5°,∠C=∠B+20°=∠A+25°
因为∠A+∠B+∠C=180°
所以∠A+∠A+5°+∠A+25°=180°
解得∠A=50°，所以∠B=∠A+5°=55°，∠C=∠A+25°=75°.
等式性质； AE∥BC； 两直线平行，内错角相等；
AF ＝BD； SAS; ∠EFA; 全等三角形对应角相等。
解：因为∠3=∠1+∠2，∠1=∠2,所以∠3=2∠1。
又因为∠3=∠4,所以∠DAC=180°-∠3-∠4=180°-2∠3=180°-4∠1.
因为∠BAC=63°，所以∠1+∠DAC=63°.
所以∠1+180°-4∠1=63°，解得∠1=39°.
所以∠DAC=63°-∠1=24°.
23、解：能，过程如下：
因为AB＝AC，所以∠B=∠C.
所以∠BAC=180°-(∠B+∠C)=180°-2∠B.
因为AB＝BD，所以∠BAD=∠BDA.
因为∠1＝30°，
所以∠BAD=∠BDA=180°-2∠B-∠1=150°-2∠B.
因为在△ABD中，∠B+∠BAD+∠BDA=180°
所以∠B+2（150°-2∠B）=180°。
解得∠B=40°，所以∠C=40°，∠BAC=100°.
24、（1）πR ; （2）πR ； （3）πR ； （4）（n-1）πR .
25、解：（1）MN⊥AC，理由如下：
因为N是AC的中点，所以AN=CN.
在△AMN与△CMN中，
所以△AMN≌△CMN（SSS）
所以∠A=∠ACM,∠ANM=∠CNM(全等三角形对应角相等）
因为N是AB上一点，
所以∠ANM=∠CNM=90°，即MN⊥AC。
△ABC是直角三角形，理由如下：
因为MN∥BC，∠ANM=90°，
所以∠ACB=∠ANM=90°(两直线平行，同位角相等）
所以△ABC是直角三角形。
（3）MB = MC，理由如下：
因为∠ACB=90°，所以∠ACM+∠MCB=90°,且∠A+∠B=90°.
因为∠A=∠ACM（已证），所以∠MCB=∠B，所以MB = MC。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)