中考复习专题--图形运动过程中的临界问题
文档属性
| 名称 | 中考复习专题--图形运动过程中的临界问题 |  | |
| 格式 | zip | ||
| 文件大小 | 264.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-25 21:57:17 | ||
图片预览

文档简介
图形运动过程中的临界问题
一、题型特点
1.图形位置不确定;
2.图形运动具有连续性;
3.多以求某一变量的取值范围或最值为主.
二、涉及的主要知识点
1.几何作图或画函数图象;
2.几何计算;
3.方程或不等式(组);
三、主要解题思路
1.通过画图(或示意图)或直观操作把问题直观化;
2.确定运动的起始位置、终止位置或某些特殊位置,化动为静;
3.计算临界位置的相应结果,得到相应变量的取值范围或最值.
四、例题讲解
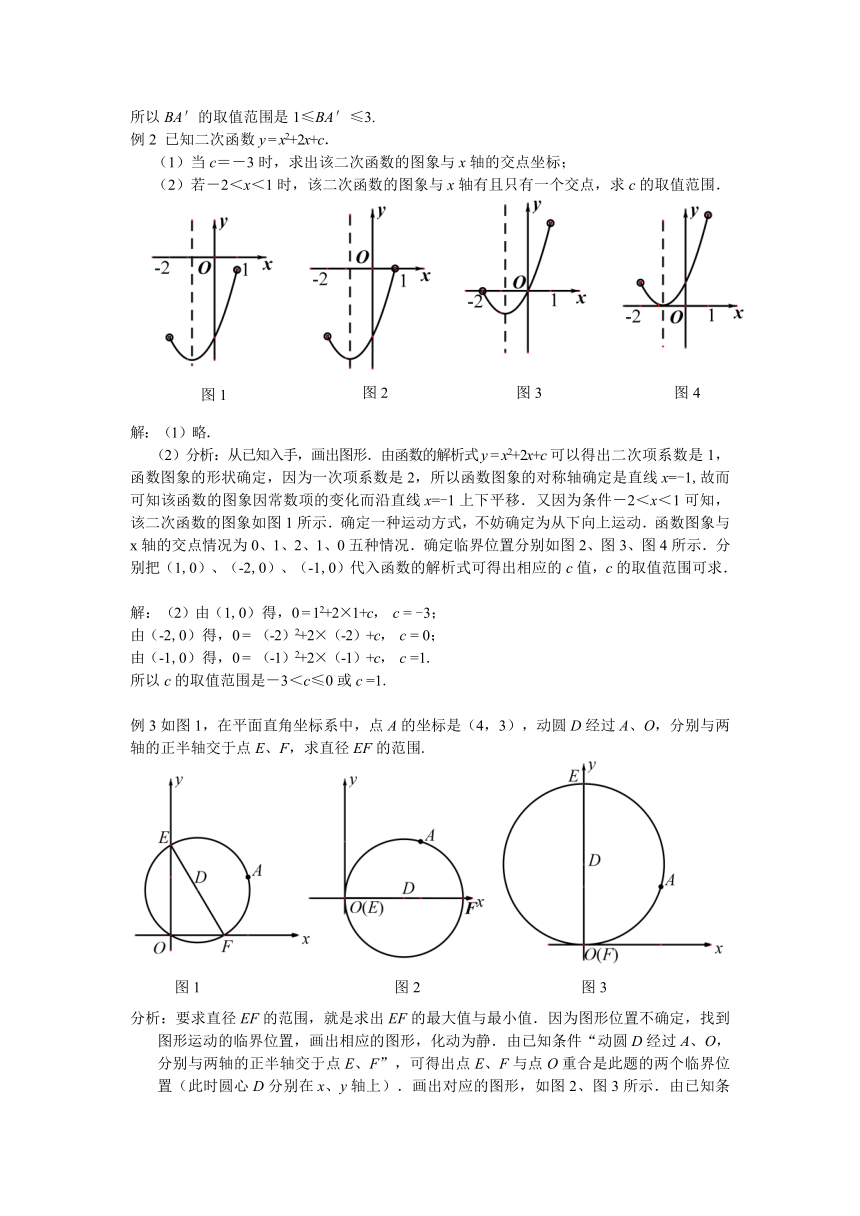
例1 在矩形纸片ABCD中,AB=3,AD=5.如图1所示,折叠纸片,使点A落在BC边上的A'处,折痕为PQ,当点A'在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则BA'的取值范围是 .
分析:如图2,解题由画图开始.点A'在BC边上移动,可首先使点A'与点B重合,画出相应的图形,如图2所示;再使点A'与点C重合,画出相应的图形,如图3所示,可知均不满足条件,进而可得出,点P、Q的位置决定BA'的取值范围.当点P与点B重合时,如图4所示,BA'值再大,当点Q与点D重合时,如图5所示,BA'值再小,BA'的取值范围可求.
解:如图4,当点P与点B重合时, BA'=3.
如图5,当点Q与点D重合时, DA'=5,CA'=5,BA'=1.
所以BA'的取值范围是1≤BA'≤3.
例2 已知二次函数y = x2+2x+c.
(1)当c=-3时,求出该二次函数的图象与x轴的交点坐标;
(2)若-2<x<1时,该二次函数的图象与x轴有且只有一个交点,求c的取值范围.
解:(1)略.
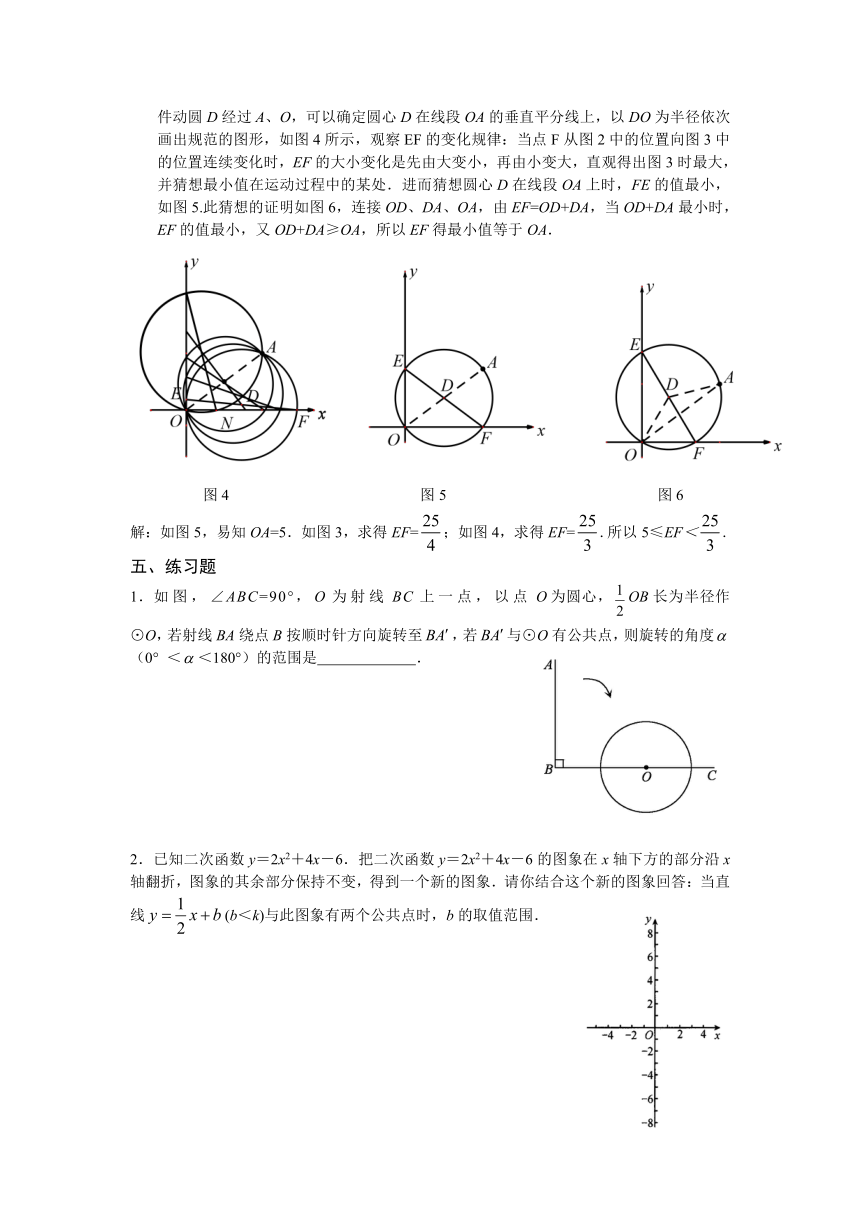
(2)分析:从已知入手,画出图形.由函数的解析式y = x2+2x+c可以得出二次项系数是1,函数图象的形状确定,因为一次项系数是2,所以函数图象的对称轴确定是直线x=-1,故而可知该函数的图象因常数项的变化而沿直线x=-1上下平移.又因为条件-2<x<1可知,该二次函数的图象如图1所示.确定一种运动方式,不妨确定为从下向上运动.函数图象与x轴的交点情况为0、1、2、1、0五种情况.确定临界位置分别如图2、图3、图4所示.分别把(1,0)、(-2,0)、(-1,0)代入函数的解析式可得出相应的c值,c的取值范围可求.
解:(2)由(1,0)得,0 = 12+2×1+c, c = -3;
由(-2,0)得,0 = (-2)2+2×(-2)+c, c = 0;
由(-1,0)得,0 = (-1)2+2×(-1)+c, c =1.
所以c的取值范围是-3<c≤0或c =1.
例3如图1,在平面直角坐标系中,点A的坐标是(4,3),动圆D经过A、O,分别与两轴的正半轴交于点E、F,求直径EF的范围.
分析:要求直径EF的范围,就是求出EF的最大值与最小值.因为图形位置不确定,找到图形运动的临界位置,画出相应的图形,化动为静.由已知条件“动圆D经过A、O,分别与两轴的正半轴交于点E、F”,可得出点E、F与点O重合是此题的两个临界位置(此时圆心D分别在x、y轴上).画出对应的图形,如图2、图3所示.由已知条件动圆D经过A、O,可以确定圆心D在线段OA的垂直平分线上,以DO为半径依次画出规范的图形,如图4所示,观察EF的变化规律:当点F从图2中的位置向图3中的位置连续变化时,EF的大小变化是先由大变小,再由小变大,直观得出图3时最大,并猜想最小值在运动过程中的某处.进而猜想圆心D在线段OA上时,FE的值最小,如图5.此猜想的证明如图6,连接OD、DA、OA,由EF=OD+DA,当OD+DA最小时,EF的值最小,又OD+DA≥OA,所以EF得最小值等于OA.
解:如图5,易知OA=5.如图3,求得EF=;如图4,求得EF=.所以5≤EF<.
五、练习题
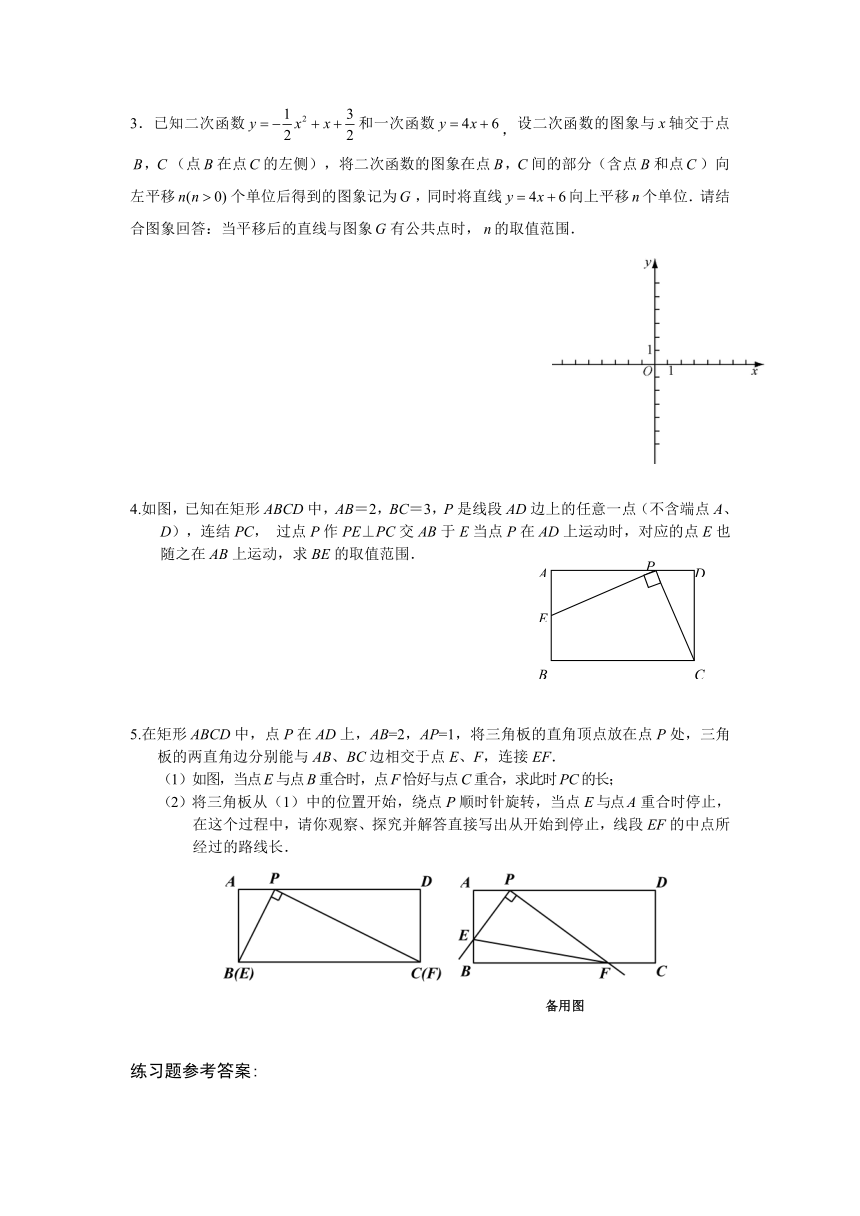
1.如图,∠ABC=90°,O为射线BC上一点,以点O为圆心,OB长为半径作⊙O,若射线BA绕点B按顺时针方向旋转至,若与⊙O有公共点,则旋转的角度(0° <<180°)的范围是 .
2.已知二次函数y=2x2+4x-6.把二次函数y=2x2+4x-6的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线(b<k)与此图象有两个公共点时,b的取值范围.
3.已知二次函数和一次函数,设二次函数的图象与轴交于点(点在点的左侧),将二次函数的图象在点间的部分(含点和点)向左平移个单位后得到的图象记为,同时将直线向上平移个单位.请结合图象回答:当平移后的直线与图象有公共点时,的取值范围.
4.如图,已知在矩形ABCD中,AB=2,BC=3,P是线段AD边上的任意一点(不含端点A、D),连结PC, 过点P作PE⊥PC交AB于E当点P在AD上运动时,对应的点E也随之在AB上运动,求BE的取值范围.
5.在矩形ABCD中,点P在AD上,AB=2,AP=1,将三角板的直角顶点放在点P处,三角板的两直角边分别能与AB、BC边相交于点E、F,连接EF.
(1)如图,当点E与点B重合时,点F恰好与点C重合,求此时PC的长;
(2)将三角板从(1)中的位置开始,绕点P顺时针旋转,当点E与点A重合时停止,在这个过程中,请你观察、探究并解答直接写出从开始到停止,线段EF的中点所经过的路线长.
备用图
练习题参考答案:
1.60° ≤≤120°
2.
3.
4. ≤BE<2
5.(1) (2)
说明:
例2是2012年北京市朝阳区九年级综合练习(二)数学试卷第22题 ;
22.已知二次函数.
(1)当c=-3时,求出该二次函数的图象与x轴的交点坐标;
(2)若-2<x<1时,该二次函数的图象与x轴有且只有一个交点,求c的取值范围.
22. 解:(1)由题意,得.
当时,.
解得,.
∴该二次函数的图象与x轴的交点坐标为(-3,0),(1,0).
(2)抛物线的对称轴为.
① 若抛物线与x轴只有一个交点,则交点为(-1,0).
有,解得.
② 若抛物线与x轴有两个交点,且满足题意,则有
当时, ≤0,
∴≤0,解得≤0.
当时,,
∴,解得.
∴≤0.
综上所述,c的取值范围是或≤0.
练习2是由2009年北京市中考数学试卷第23题改编
原题及答案
23.已知关于x的一元二次方程2x2+4x+k-1=0有实数根,k为正整数.
(1)求k的值;
(2)当此方程有两个非零的整数根时,将关于x的二次函数y=2x2+4x+k-1的图象向下平移8个单位长度,求平移后的图象的解析式;
(3)在(2)的条件下,将平移后的二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线(b<k)与此图象有两个公共点时,b的取值范围.
第23题图
23.解:(1)由题意得,Δ=16-8(k-1)≥0.∴k≤3.
∵k为正整数,∴k=1,2,3.
(2)当k=1时,方程2x2+4x+k-1=0有一个根为零;
当k=2时,方程2x2+4x+k-1=0无整数根;
当k=3时,方程2x2+4x+k-1=0有两个非零的整数根.
综上所述,k=1和k=2不合题意,舍去;k=3符合题意.
当k=3时,二次函数为y=2x2+4x+2,把它的图象向下平移8个单位长度得到的图象的解析式为y=2x2+4x-6.
(3)设二次函数y=2x2+4x-6的图象与x轴交于A、B两点,则A(-3,0),B(1,0).
依题意翻折后的图象如图所示.
第23题答图
当直线经过A点时,可得;
当直线经过B点时,可得.
由图象可知,符合题意的b(b<3)的取值范围为.
练习3是由2012年北京中考数学试卷第23题改编
原题及答案
23.已知二次函数
在和时的函数值相等。
求二次函数的解析式;
若一次函数的图象与二次函数的图象都经过点,求和的值;
设二次函数的图象与轴交于点(点在点的左侧),将二次函数的图象在点间的部分(含点和点)向左平移个单位后得到的图象记为,同时将(2)中得到的直线向上平移个单位。请结合图象回答:当平移后的直线与图象有公共点时,的取值范围。
23. 解:(1)由题意得.
解得.
二次函数的解析式为.
(2)点在二次函数的图象上,
.
点的坐标为.
点在一次函数的图象上,
.
(3)由题意,可得点的坐标分别为.
平移后,点的对应点分别为
.
将直线平移后得到直线
.
如图1,当直线经过
点时,图象(点除外)
在该直线右侧,可得;
如图2,当直线经过
点时,图象(点除外)
在该直线左侧,可得.
由图象可知,符合题意的的取值范围是.
练习5是2012年北京市朝阳区九年级综合练习(一)数学试卷第25题(有改动),原题及答案如下:
25. 在矩形ABCD中,点P在AD上,AB=2,AP=1,将三角板的直角顶点放在点P处,三角板的两直角边分别能与AB、BC边相交于点E、F,连接EF.
(1)如图,当点E与点B重合时,点F恰好与点C重合,求此时PC的长;
(2)将三角板从(1)中的位置开始,绕点P顺时针旋转,当点E与点A重合时停止,在这个过程中,请你观察、探究并解答:
① ∠PEF的大小是否发生变化?请说明理由;
② 直接写出从开始到停止,线段EF的中点所经过的路线长.
备用图
25. 解:(1)在矩形ABCD中,,AP=1,CD=AB=2,
∴PB= ,.
∵,
∴.
∴.
∴ △ABP∽△DPC.
∴,即.
∴PC=2.
(2)① ∠PEF的大小不变.
理由:过点F作FG⊥AD于点G.
∴四边形ABFG是矩形.
∴.
∴GF=AB=2,.
∵,
∴.
∴.
∴ △APE∽△GFP.
∴.
∴在Rt△EPF中,tan∠PEF=.
即tan∠PEF的值不变.
∴∠PEF的大小不变.
② .
一、题型特点
1.图形位置不确定;
2.图形运动具有连续性;
3.多以求某一变量的取值范围或最值为主.
二、涉及的主要知识点
1.几何作图或画函数图象;
2.几何计算;
3.方程或不等式(组);
三、主要解题思路
1.通过画图(或示意图)或直观操作把问题直观化;
2.确定运动的起始位置、终止位置或某些特殊位置,化动为静;
3.计算临界位置的相应结果,得到相应变量的取值范围或最值.
四、例题讲解
例1 在矩形纸片ABCD中,AB=3,AD=5.如图1所示,折叠纸片,使点A落在BC边上的A'处,折痕为PQ,当点A'在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则BA'的取值范围是 .
分析:如图2,解题由画图开始.点A'在BC边上移动,可首先使点A'与点B重合,画出相应的图形,如图2所示;再使点A'与点C重合,画出相应的图形,如图3所示,可知均不满足条件,进而可得出,点P、Q的位置决定BA'的取值范围.当点P与点B重合时,如图4所示,BA'值再大,当点Q与点D重合时,如图5所示,BA'值再小,BA'的取值范围可求.
解:如图4,当点P与点B重合时, BA'=3.
如图5,当点Q与点D重合时, DA'=5,CA'=5,BA'=1.
所以BA'的取值范围是1≤BA'≤3.
例2 已知二次函数y = x2+2x+c.
(1)当c=-3时,求出该二次函数的图象与x轴的交点坐标;
(2)若-2<x<1时,该二次函数的图象与x轴有且只有一个交点,求c的取值范围.
解:(1)略.
(2)分析:从已知入手,画出图形.由函数的解析式y = x2+2x+c可以得出二次项系数是1,函数图象的形状确定,因为一次项系数是2,所以函数图象的对称轴确定是直线x=-1,故而可知该函数的图象因常数项的变化而沿直线x=-1上下平移.又因为条件-2<x<1可知,该二次函数的图象如图1所示.确定一种运动方式,不妨确定为从下向上运动.函数图象与x轴的交点情况为0、1、2、1、0五种情况.确定临界位置分别如图2、图3、图4所示.分别把(1,0)、(-2,0)、(-1,0)代入函数的解析式可得出相应的c值,c的取值范围可求.
解:(2)由(1,0)得,0 = 12+2×1+c, c = -3;
由(-2,0)得,0 = (-2)2+2×(-2)+c, c = 0;
由(-1,0)得,0 = (-1)2+2×(-1)+c, c =1.
所以c的取值范围是-3<c≤0或c =1.
例3如图1,在平面直角坐标系中,点A的坐标是(4,3),动圆D经过A、O,分别与两轴的正半轴交于点E、F,求直径EF的范围.
分析:要求直径EF的范围,就是求出EF的最大值与最小值.因为图形位置不确定,找到图形运动的临界位置,画出相应的图形,化动为静.由已知条件“动圆D经过A、O,分别与两轴的正半轴交于点E、F”,可得出点E、F与点O重合是此题的两个临界位置(此时圆心D分别在x、y轴上).画出对应的图形,如图2、图3所示.由已知条件动圆D经过A、O,可以确定圆心D在线段OA的垂直平分线上,以DO为半径依次画出规范的图形,如图4所示,观察EF的变化规律:当点F从图2中的位置向图3中的位置连续变化时,EF的大小变化是先由大变小,再由小变大,直观得出图3时最大,并猜想最小值在运动过程中的某处.进而猜想圆心D在线段OA上时,FE的值最小,如图5.此猜想的证明如图6,连接OD、DA、OA,由EF=OD+DA,当OD+DA最小时,EF的值最小,又OD+DA≥OA,所以EF得最小值等于OA.
解:如图5,易知OA=5.如图3,求得EF=;如图4,求得EF=.所以5≤EF<.
五、练习题
1.如图,∠ABC=90°,O为射线BC上一点,以点O为圆心,OB长为半径作⊙O,若射线BA绕点B按顺时针方向旋转至,若与⊙O有公共点,则旋转的角度(0° <<180°)的范围是 .
2.已知二次函数y=2x2+4x-6.把二次函数y=2x2+4x-6的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线(b<k)与此图象有两个公共点时,b的取值范围.
3.已知二次函数和一次函数,设二次函数的图象与轴交于点(点在点的左侧),将二次函数的图象在点间的部分(含点和点)向左平移个单位后得到的图象记为,同时将直线向上平移个单位.请结合图象回答:当平移后的直线与图象有公共点时,的取值范围.
4.如图,已知在矩形ABCD中,AB=2,BC=3,P是线段AD边上的任意一点(不含端点A、D),连结PC, 过点P作PE⊥PC交AB于E当点P在AD上运动时,对应的点E也随之在AB上运动,求BE的取值范围.
5.在矩形ABCD中,点P在AD上,AB=2,AP=1,将三角板的直角顶点放在点P处,三角板的两直角边分别能与AB、BC边相交于点E、F,连接EF.
(1)如图,当点E与点B重合时,点F恰好与点C重合,求此时PC的长;
(2)将三角板从(1)中的位置开始,绕点P顺时针旋转,当点E与点A重合时停止,在这个过程中,请你观察、探究并解答直接写出从开始到停止,线段EF的中点所经过的路线长.
备用图
练习题参考答案:
1.60° ≤≤120°
2.
3.
4. ≤BE<2
5.(1) (2)
说明:
例2是2012年北京市朝阳区九年级综合练习(二)数学试卷第22题 ;
22.已知二次函数.
(1)当c=-3时,求出该二次函数的图象与x轴的交点坐标;
(2)若-2<x<1时,该二次函数的图象与x轴有且只有一个交点,求c的取值范围.
22. 解:(1)由题意,得.
当时,.
解得,.
∴该二次函数的图象与x轴的交点坐标为(-3,0),(1,0).
(2)抛物线的对称轴为.
① 若抛物线与x轴只有一个交点,则交点为(-1,0).
有,解得.
② 若抛物线与x轴有两个交点,且满足题意,则有
当时, ≤0,
∴≤0,解得≤0.
当时,,
∴,解得.
∴≤0.
综上所述,c的取值范围是或≤0.
练习2是由2009年北京市中考数学试卷第23题改编
原题及答案
23.已知关于x的一元二次方程2x2+4x+k-1=0有实数根,k为正整数.
(1)求k的值;
(2)当此方程有两个非零的整数根时,将关于x的二次函数y=2x2+4x+k-1的图象向下平移8个单位长度,求平移后的图象的解析式;
(3)在(2)的条件下,将平移后的二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线(b<k)与此图象有两个公共点时,b的取值范围.
第23题图
23.解:(1)由题意得,Δ=16-8(k-1)≥0.∴k≤3.
∵k为正整数,∴k=1,2,3.
(2)当k=1时,方程2x2+4x+k-1=0有一个根为零;
当k=2时,方程2x2+4x+k-1=0无整数根;
当k=3时,方程2x2+4x+k-1=0有两个非零的整数根.
综上所述,k=1和k=2不合题意,舍去;k=3符合题意.
当k=3时,二次函数为y=2x2+4x+2,把它的图象向下平移8个单位长度得到的图象的解析式为y=2x2+4x-6.
(3)设二次函数y=2x2+4x-6的图象与x轴交于A、B两点,则A(-3,0),B(1,0).
依题意翻折后的图象如图所示.
第23题答图
当直线经过A点时,可得;
当直线经过B点时,可得.
由图象可知,符合题意的b(b<3)的取值范围为.
练习3是由2012年北京中考数学试卷第23题改编
原题及答案
23.已知二次函数
在和时的函数值相等。
求二次函数的解析式;
若一次函数的图象与二次函数的图象都经过点,求和的值;
设二次函数的图象与轴交于点(点在点的左侧),将二次函数的图象在点间的部分(含点和点)向左平移个单位后得到的图象记为,同时将(2)中得到的直线向上平移个单位。请结合图象回答:当平移后的直线与图象有公共点时,的取值范围。
23. 解:(1)由题意得.
解得.
二次函数的解析式为.
(2)点在二次函数的图象上,
.
点的坐标为.
点在一次函数的图象上,
.
(3)由题意,可得点的坐标分别为.
平移后,点的对应点分别为
.
将直线平移后得到直线
.
如图1,当直线经过
点时,图象(点除外)
在该直线右侧,可得;
如图2,当直线经过
点时,图象(点除外)
在该直线左侧,可得.
由图象可知,符合题意的的取值范围是.
练习5是2012年北京市朝阳区九年级综合练习(一)数学试卷第25题(有改动),原题及答案如下:
25. 在矩形ABCD中,点P在AD上,AB=2,AP=1,将三角板的直角顶点放在点P处,三角板的两直角边分别能与AB、BC边相交于点E、F,连接EF.
(1)如图,当点E与点B重合时,点F恰好与点C重合,求此时PC的长;
(2)将三角板从(1)中的位置开始,绕点P顺时针旋转,当点E与点A重合时停止,在这个过程中,请你观察、探究并解答:
① ∠PEF的大小是否发生变化?请说明理由;
② 直接写出从开始到停止,线段EF的中点所经过的路线长.
备用图
25. 解:(1)在矩形ABCD中,,AP=1,CD=AB=2,
∴PB= ,.
∵,
∴.
∴.
∴ △ABP∽△DPC.
∴,即.
∴PC=2.
(2)① ∠PEF的大小不变.
理由:过点F作FG⊥AD于点G.
∴四边形ABFG是矩形.
∴.
∴GF=AB=2,.
∵,
∴.
∴.
∴ △APE∽△GFP.
∴.
∴在Rt△EPF中,tan∠PEF=.
即tan∠PEF的值不变.
∴∠PEF的大小不变.
② .
同课章节目录
