人教版八年级下册 16.1二次根式课件(共27张PPT)
文档属性
| 名称 | 人教版八年级下册 16.1二次根式课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 16:34:31 | ||
图片预览







文档简介
(共27张PPT)
二次根式
⑵什么是一个数的算术平方根?如何表示?
正数的正的平方根叫做它的算术平方根。
复习
⑴什么叫做一个数的平方根?如何表示?
一般地,若一个数的平方等于a,则
这个数就叫做a的平方根。
用 (a≥0)表示。
0的算术平方根是0
a的平方根是
正数有两个平方根且互为相反数;
0有一个平方根就是0;
负数没有平方根。
1、平方根的性质:
1、16的平方根是什么 算术平方根是什么?
2、0的平方根是什么?算术平方根是什么?
3、-7有没有平方根?有没有算术平方根?
2S
④
9
①
10
②
S
③
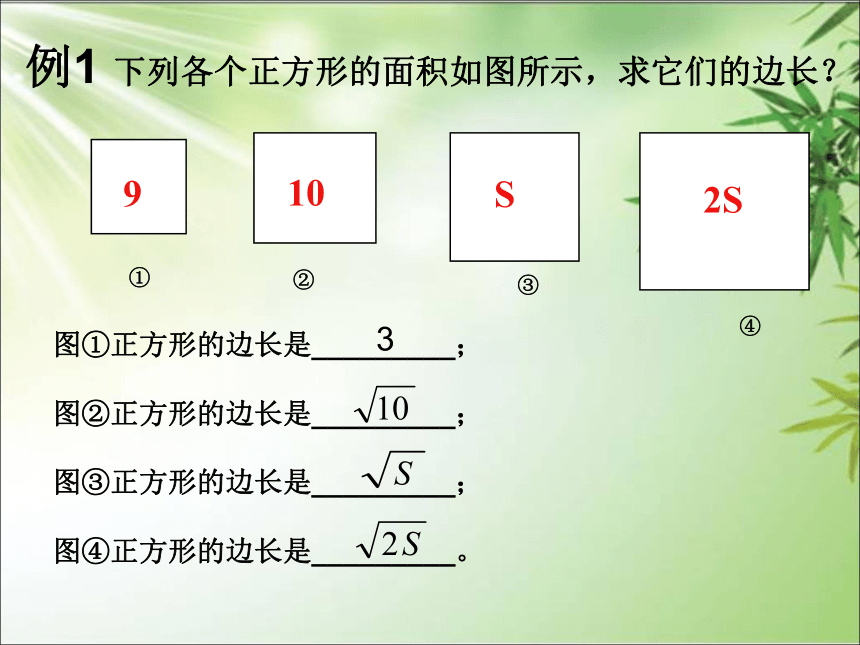
例1 下列各个正方形的面积如图所示,求它们的边长?
图①正方形的边长是_________;
图②正方形的边长是_________;
图③正方形的边长是_________;
图④正方形的边长是_________。
3
这些式子有什么共同特征?
(1)都含有根号且根号的指数是2;
(2)被开方数为非负数。
上面问题中得到的结果
分别是: , , , 。
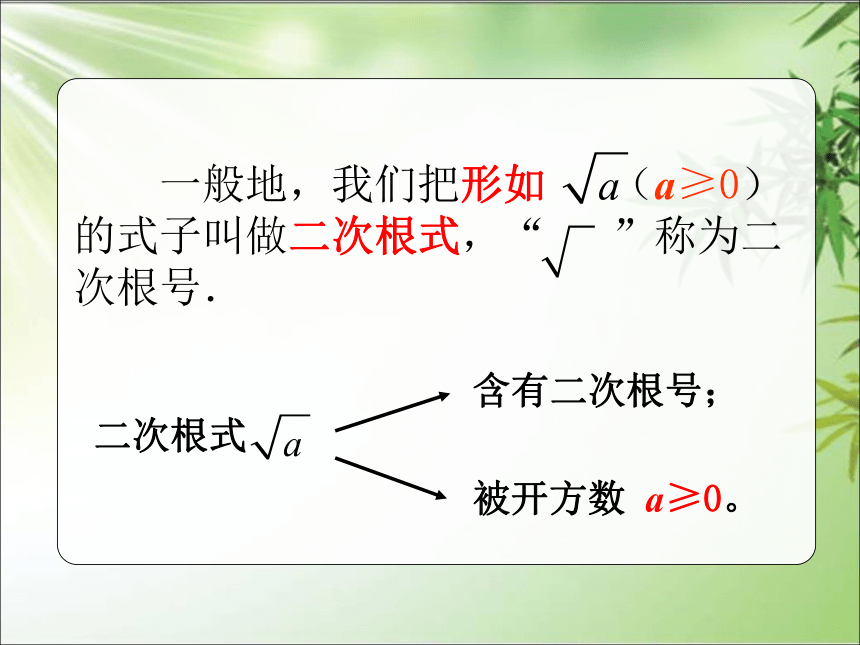
被开方数 a≥0。
含有二次根号;
二次根式
一般地,我们把形如 (a≥0)的式子叫做二次根式,“ ”称为二次根号.
下列各式是二次根式吗
(m≤0),
(x,y 异号)
(9)
(10)
求下列二次根式中字母的取值范围:
1、 x取何值时,下列式子有意义
求式子中字母的取值范围的基本依据:
①二次根式被开方数为非负数;
②式中含有分式时,要保证分母不为零。
③式中含有零指数或负整数指数时,
要保证底数不为0。
2.已知a.b为实数,且满足
你能求出a+b 的值吗?
若 ,求a,b的值
3、已知 有意义,那P(a, b)在 象限.
第三
4、 的最小值为__,此时x的值为__。
2
3
探究
2
4
17
0
一般地,
(a≥0)
归纳
例题讲解
计算:
解:
练习
解:
探究
2
0.1
0
一般地,根据算术平方根的意义,
a
-a
(a≥0)
(a≤0)
例题讲解
化简:
解:
练习
8
3
12
6
计算:
练习2:
(x﹤y)
(x>0 )
2.从取值范围来看,
a≥0
a取任何实数
1:从运算顺序来看,
先开方,后平方
先平方,后开方
3.从运算结果来看:
=a
a (a≥ 0)
-a (a≤0)
=
=∣a∣
化简下列各式:
(河南省)实数p在数轴上的位置如图所示,化简
1.若1<x<4,则化简
的结果是_____
2.设a,b,c为△ ABC的三边,化简
3
2a+2b+2c
代数式
≥
代数式
注:代数式中不含等号或不等号
(1)二次根式的概念
(2)根号内字母的取值范围
(3)二次根式的性质
二次根式
⑵什么是一个数的算术平方根?如何表示?
正数的正的平方根叫做它的算术平方根。
复习
⑴什么叫做一个数的平方根?如何表示?
一般地,若一个数的平方等于a,则
这个数就叫做a的平方根。
用 (a≥0)表示。
0的算术平方根是0
a的平方根是
正数有两个平方根且互为相反数;
0有一个平方根就是0;
负数没有平方根。
1、平方根的性质:
1、16的平方根是什么 算术平方根是什么?
2、0的平方根是什么?算术平方根是什么?
3、-7有没有平方根?有没有算术平方根?
2S
④
9
①
10
②
S
③
例1 下列各个正方形的面积如图所示,求它们的边长?
图①正方形的边长是_________;
图②正方形的边长是_________;
图③正方形的边长是_________;
图④正方形的边长是_________。
3
这些式子有什么共同特征?
(1)都含有根号且根号的指数是2;
(2)被开方数为非负数。
上面问题中得到的结果
分别是: , , , 。
被开方数 a≥0。
含有二次根号;
二次根式
一般地,我们把形如 (a≥0)的式子叫做二次根式,“ ”称为二次根号.
下列各式是二次根式吗
(m≤0),
(x,y 异号)
(9)
(10)
求下列二次根式中字母的取值范围:
1、 x取何值时,下列式子有意义
求式子中字母的取值范围的基本依据:
①二次根式被开方数为非负数;
②式中含有分式时,要保证分母不为零。
③式中含有零指数或负整数指数时,
要保证底数不为0。
2.已知a.b为实数,且满足
你能求出a+b 的值吗?
若 ,求a,b的值
3、已知 有意义,那P(a, b)在 象限.
第三
4、 的最小值为__,此时x的值为__。
2
3
探究
2
4
17
0
一般地,
(a≥0)
归纳
例题讲解
计算:
解:
练习
解:
探究
2
0.1
0
一般地,根据算术平方根的意义,
a
-a
(a≥0)
(a≤0)
例题讲解
化简:
解:
练习
8
3
12
6
计算:
练习2:
(x﹤y)
(x>0 )
2.从取值范围来看,
a≥0
a取任何实数
1:从运算顺序来看,
先开方,后平方
先平方,后开方
3.从运算结果来看:
=a
a (a≥ 0)
-a (a≤0)
=
=∣a∣
化简下列各式:
(河南省)实数p在数轴上的位置如图所示,化简
1.若1<x<4,则化简
的结果是_____
2.设a,b,c为△ ABC的三边,化简
3
2a+2b+2c
代数式
≥
代数式
注:代数式中不含等号或不等号
(1)二次根式的概念
(2)根号内字母的取值范围
(3)二次根式的性质
