中考数学复习之无刻度直尺作图问题(含答案)
文档属性
| 名称 | 中考数学复习之无刻度直尺作图问题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 737.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 00:00:00 | ||
图片预览


文档简介
无刻度直尺作图举例及练习题
问题简介
问题特点
1.无刻度直尺;2.利用特殊点进行作图;3.对图形性质要非常高;
包含的问题:1.角度问题;2.对称问题;3.旋转问题;4.特殊角问题;5.特殊图形问题;6.切线问题;
问题举例
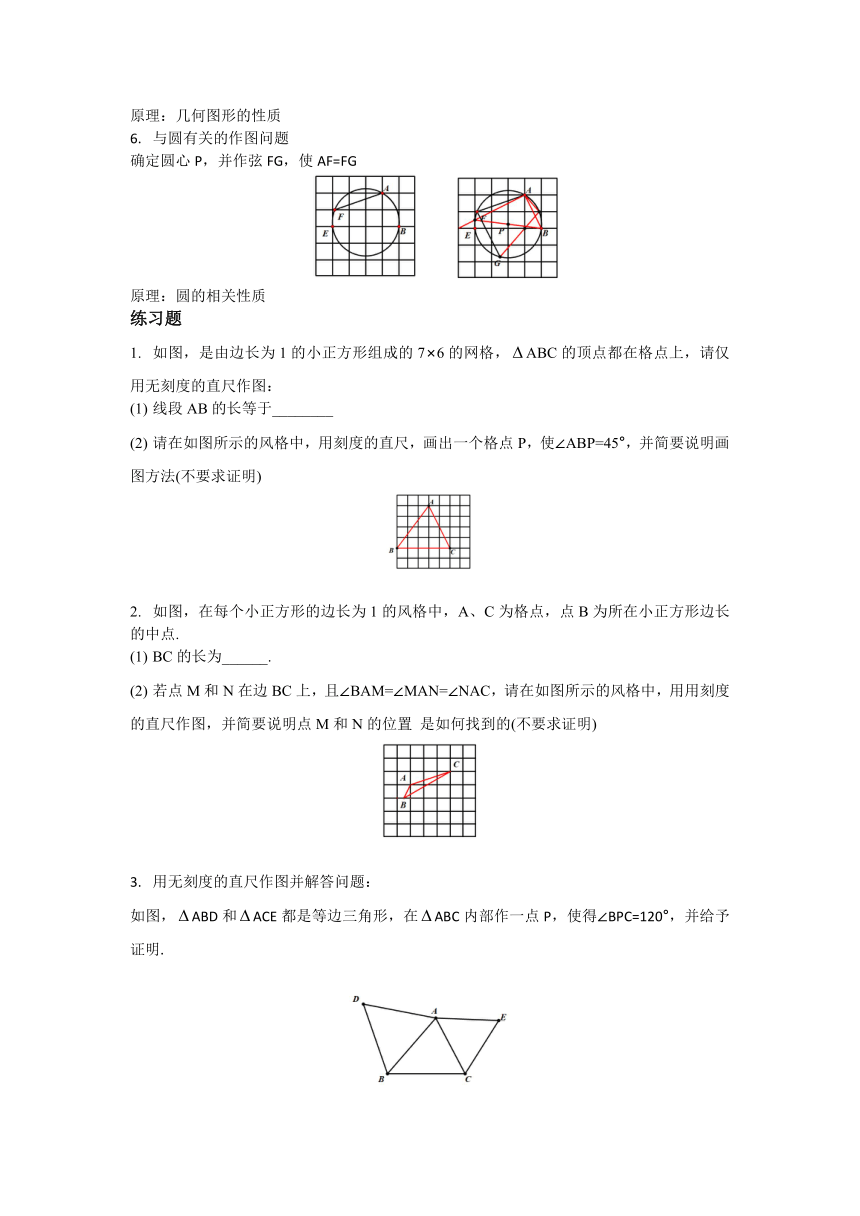
1.特殊角问题:找一格点C,使∠BAC=45°
原理:tan=,tan=,则=45°
2.找中点:作线段AB的中点P
原理:平行线分线段成比例
3.找n等分点
原理:平行线分线段成比例
作垂线
原理:平移及全等
作特殊图形
E为正方形对角线上一点,BE>DE,作以AE为边的菱形
原理:几何图形的性质
与圆有关的作图问题
确定圆心P,并作弦FG,使AF=FG
原理:圆的相关性质
练习题
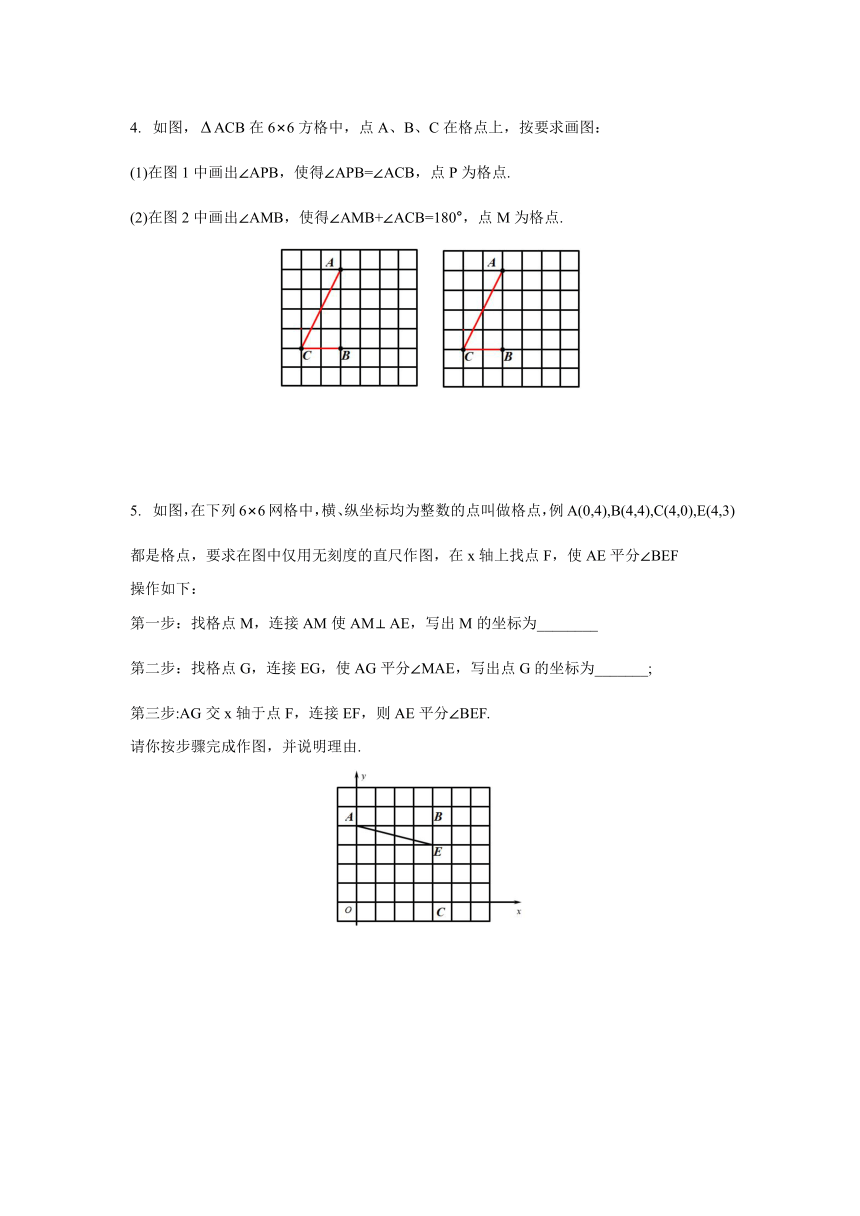
如图,是由边长为1的小正方形组成的7×6的网格,ABC的顶点都在格点上,请仅用无刻度的直尺作图:
线段AB的长等于________
请在如图所示的风格中,用刻度的直尺,画出一个格点P,使∠ABP=45°,并简要说明画图方法(不要求证明)
如图,在每个小正方形的边长为1的风格中,A、C为格点,点B为所在小正方形边长的中点.
BC的长为______.
若点M和N在边BC上,且∠BAM=∠MAN=∠NAC,请在如图所示的风格中,用用刻度的直尺作图,并简要说明点M和N的位置 是如何找到的(不要求证明)
用无刻度的直尺作图并解答问题:
如图,ABD和ACE都是等边三角形,在ABC内部作一点P,使得∠BPC=120°,并给予证明.
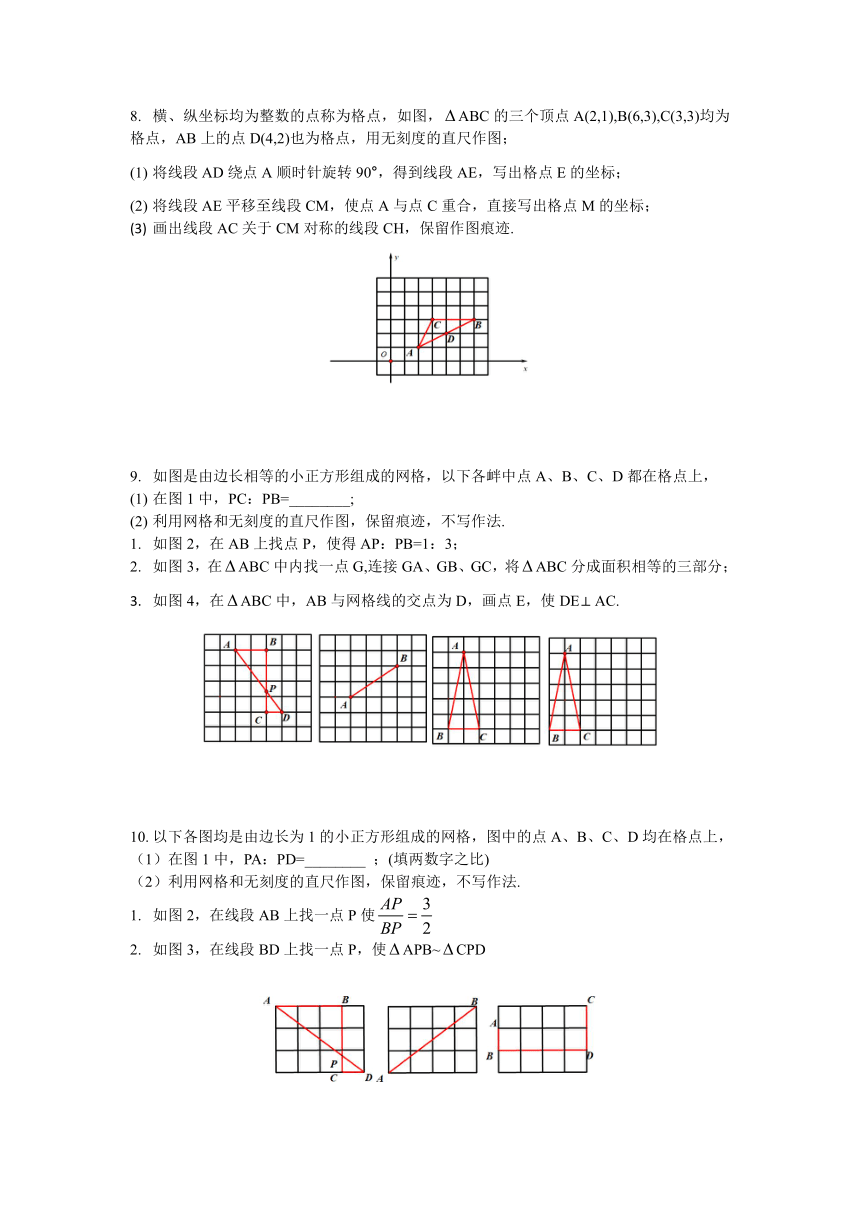
如图,ACB在6×6方格中,点A、B、C在格点上,按要求画图:
(1)在图1中画出∠APB,使得∠APB=∠ACB,点P为格点.
(2)在图2中画出∠AMB,使得∠AMB+∠ACB=180°,点M为格点.
如图,在下列6×6网格中,横、纵坐标均为整数的点叫做格点,例A(0,4),B(4,4),C(4,0),E(4,3)都是格点,要求在图中仅用无刻度的直尺作图,在x轴上找点F,使AE平分∠BEF
操作如下:
第一步:找格点M,连接AM使AM AE,写出M的坐标为________
第二步:找格点G,连接EG,使AG平分∠MAE,写出点G的坐标为_______;
第三步:AG交x轴于点F,连接EF,则AE平分∠BEF.
请你按步骤完成作图,并说明理由.
用无刻度的直尺作图(辅助线请画虚线)
(1)如图1,在 ABCD中画一条直线平分周长;
(2)如图2,在O中,AB为O内的一条弦,D为优弧AB的中点,C为优弧AB的一动点,画出∠ACB的平分线;
(3)如图3,在正方形ABCD中,E为CB上的任意一点,在AB上截取一点F,使得BF=BE.
如图,在下列10×10的风格中,横、纵坐标均为整点的数叫做格点,例如A(-2,-2),B(5,-3),C(1,2)都是格点.
(1)∠ACB的大小为________
(2)要求在下图中仅用无刻度的直尺作图:以A为中心,取旋转角等于∠BAC.
把ABC逆时针旋转,得到ABC,其中点C和点B的对应点分别为点C和B,操作步骤如下:
第一步:延长AC到格点B1,使得AB1=AB;
第二步:延长BC到格点E,使得CE=CB,连接AE;
第三步:取格点F,连接FB1交AE于点C1,则AB1C1即为所示.
请你按步骤完成作图,并直接写出B1、E、F三点的坐标.
横、纵坐标均为整数的点称为格点,如图,ABC的三个顶点A(2,1),B(6,3),C(3,3)均为格点,AB上的点D(4,2)也为格点,用无刻度的直尺作图;
将线段AD绕点A顺时针旋转90°,得到线段AE,写出格点E的坐标;
将线段AE平移至线段CM,使点A与点C重合,直接写出格点M的坐标;
画出线段AC关于CM对称的线段CH,保留作图痕迹.
如图是由边长相等的小正方形组成的网格,以下各衅中点A、B、C、D都在格点上,
在图1中,PC:PB=________;
利用网格和无刻度的直尺作图,保留痕迹,不写作法.
如图2,在AB上找点P,使得AP:PB=1:3;
如图3,在ABC中内找一点G,连接GA、GB、GC,将ABC分成面积相等的三部分;
如图4,在ABC中,AB与网格线的交点为D,画点E,使DE AC.
以下各图均是由边长为1的小正方形组成的网格,图中的点A、B、C、D均在格点上,
在图1中,PA:PD=________ ;(填两数字之比)
利用网格和无刻度的直尺作图,保留痕迹,不写作法.
如图2,在线段AB上找一点P使
如图3,在线段BD上找一点P,使APB~CPD
请用无刻度的直尺作图.
在图1中,已知点E是正方形ABCD边AB的中点,画出CD的中点F;
图2是正方形ABCD,E是对角线BD上任意一点(BE>DE),以AE为边画一个菱形.
按要求作图,不要求写作法,但要保留作图痕迹.
(1)如图1,矩形ABCD的顶点A、D在圆上,B、C两点在圆心,已知圆心O请仅用无刻度的直尺作图,请作出直线l AD
(2)请仅用无刻度的直尺在下列图2和图3中按要求作图.(补上所作图开顶点字母)
1.图2是矩形ABCD,E、F分别是AB和AD的中点,以EF为边作一个菱形;
2.图4是矩形ABCD,E是对角线BD上任意一点(BE>DE),以AE为边作一个平行四边形.
已知正方形ABCD的边长为4个单位长度,点E是CD的中点,请仅用无刻度的直尺按下列要求作图(保留作图痕迹)
在图1中,将直线AC绕着正方形ABCD的中心顺时针旋转45°
在图2中,将直线AC向上平移1个单位长度.
如图平行四边形ABCD,E在AD边上,且DE=CD,仅用无刻度的直尺作图并保留作图痕迹,不写画法.
在图1中,来出∠C的角平分线;
在图2中,画出∠A的角平分线.
15.如图是边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点,在四边形ABDC中,
请你使用无刻度直尺作图,并保留作图痕迹.
(1)在直线BD上有一动点F,连接AF、FC,请作出点F使得(AF+FC)为最小值.
(2)在线段AB上有一点M,使S△ACM:S△BFM=4:1,请你画出点M的位置.
(3)延长FM、CD交于E,连接CM,请直接写出=________ ,S△CME=_______ .
16.如图,矩形ABCD与圆O交于点D,点A为圆O上一点,AB=2BC,请仅用无刻度的直尺,
分别按下列要求作图(保留作图痕迹)
(1)在图1中作出过点D的切线;
(2)在图2中作一个圆周角,使这个角的正切值为
17.在如图的网格中建立平面直角坐标系,△ABP的顶点坐标分别为A(0,3),B(1,0)P(3,2),仅用无刻度的直尺在给定网格中完成画图,画图过程中用虚线表示,并回答下列问题:
(1)在图1中,作线段CD,使P为线段CD与线段AB的位似中心,且满足
(2)在图2中,作出△PAB的外心M,并直接写出M的坐标______
(3)在图2中,作出△PAB的外接圆的切线PE.
如图,是由小正方形构成的6×6风格,每个小正方形的顶点叫做格点,圆P经过A、B两个格点,仅用无刻度的直尺在给定网格中按要求画图(画图过程用虚线表示,画图结果有实线表示)
(1)在图1中,圆P经过格点C,画圆心P,并画弦BD,使BD平分∠ABC
(2)在图2中,圆P经过格点E,F是圆P与网格线的交点,画圆心P,并画弦FG,使FG=FA.
扩展:1.圆P经过格点A,与格线交于点C,在圆上求作点D(不同于A),使CD=CA.
2.如图,圆P经过格点A,与格线交于点B,在圆上求作点E(不同于A,使AE=AB.
如图,已知A、B、C均在圆O上,请用无刻度的直尺作图,
(1)如图1,若点D是AC的中点,试画出∠B的平分线;
(2)如图2,若BD||AC,试画出∠ABC的平分线.
已知形ABCD的顶点A、D在圆上,B、C两点在圆内,请仅用无刻度的直尺作图.
(1)如图1,已知圆心O,请作出直线l AD
(2)如图2,未知圆心O,请作为直线l AD.
用无刻度的直尺作图,保留作图痕迹.
ABCD的边CD切⊙O于D
①在图1中CD上确定N点,使ON等分 ABCD的面积
②在如图2中,作CD边的高BH
ABCD的边CD与⊙O相切
①在图3中作OM CD于M;
②在图4中作CD边的垂线BH.
如图,在下列6×6的网格中,横、纵坐标均为整数的点叫做格点,例如A(0,3),B(5,3),C(1,5),D(3,4)都是格点,在网格中仅用无刻度的直尺作图,画图过程用虚线表示,画图结果用实线表示,并回答下列问题
直线写出ABC的形状;
画出点D关于AB的对称点E,并写出点E的坐标;
在线段AB上找一点F,连接F,使DF||AC;
在线段AB上确定一点M使得tan∠ACM=
23.如图,每个小正方形的边长都是1的方格纸中,有线段AC和EF,点A、C、E、F都在小正方形的顶点上.
(1)在方格纸中画出一个以线段AC为对角线的正方形ABCD,
所画的正方形的各顶点必须在小正方形的顶点上.
(2)在方格纸中以EF为腰画出等腰三角形EFM,点M在小正方形的顶点上,且MF=MC.
(3)在(1)、(2)的条件下,连接MA,请直接写出线段MA的长.
24.如图,在含有60°角的5×6菱形网格中,我们把顶点都在格点上的多边形称为格点多边形,
A,B均在格点上,按下面要求画出格点多边形.
(1)在图1中画出一个等腰三角形ABC.
(2)在图2中画出一个菱形APBQ.
参考答案
(1)AB=5 (2)原理:ABDPAE可得ABP为等腰直角三角形,故∠ABP=45°
(1)BC= (2)原理:12345原理
原理:连接BE、CE交点即为所示的点P,证明:ACDAEB,可∠ADC=∠ABE,∠BPD=180°-∠BDP-∠DBA-∠ABP=180°-∠BDP-60°-∠ADC=60°,故∠BPC=120°
原理:平行边形、等腰三角形的性质,共圆的性质;
原理:弦图垂直的性质、同余
原理:平行四边形、圆、正方形的性质
∠BAC=90°,B1(3,3),E(-3,5),F(-4,2)
E(3,-1),M(4,1)原理:全等,平移.
1:2
3:1
原理:平行四边形、矩形的对称性
原理:正方形的性质
原理:角平分与平行、等腰、中心对称图形
,
原理:圆与矩形的性质
原理:垂直平分线、位似、成比例线段
原理:圆的性质
扩展:
原理:垂径定理
20.原理:垂直径定理、矩形的性质
21.原理:矩形的性质、圆的性质、平行线分线段成比例
22.原理:平行线分线段成比例
23.原理:垂直平分线的性质、弦图性质
24.原理:全等及菱形的性质
问题简介
问题特点
1.无刻度直尺;2.利用特殊点进行作图;3.对图形性质要非常高;
包含的问题:1.角度问题;2.对称问题;3.旋转问题;4.特殊角问题;5.特殊图形问题;6.切线问题;
问题举例
1.特殊角问题:找一格点C,使∠BAC=45°
原理:tan=,tan=,则=45°
2.找中点:作线段AB的中点P
原理:平行线分线段成比例
3.找n等分点
原理:平行线分线段成比例
作垂线
原理:平移及全等
作特殊图形
E为正方形对角线上一点,BE>DE,作以AE为边的菱形
原理:几何图形的性质
与圆有关的作图问题
确定圆心P,并作弦FG,使AF=FG
原理:圆的相关性质
练习题
如图,是由边长为1的小正方形组成的7×6的网格,ABC的顶点都在格点上,请仅用无刻度的直尺作图:
线段AB的长等于________
请在如图所示的风格中,用刻度的直尺,画出一个格点P,使∠ABP=45°,并简要说明画图方法(不要求证明)
如图,在每个小正方形的边长为1的风格中,A、C为格点,点B为所在小正方形边长的中点.
BC的长为______.
若点M和N在边BC上,且∠BAM=∠MAN=∠NAC,请在如图所示的风格中,用用刻度的直尺作图,并简要说明点M和N的位置 是如何找到的(不要求证明)
用无刻度的直尺作图并解答问题:
如图,ABD和ACE都是等边三角形,在ABC内部作一点P,使得∠BPC=120°,并给予证明.
如图,ACB在6×6方格中,点A、B、C在格点上,按要求画图:
(1)在图1中画出∠APB,使得∠APB=∠ACB,点P为格点.
(2)在图2中画出∠AMB,使得∠AMB+∠ACB=180°,点M为格点.
如图,在下列6×6网格中,横、纵坐标均为整数的点叫做格点,例A(0,4),B(4,4),C(4,0),E(4,3)都是格点,要求在图中仅用无刻度的直尺作图,在x轴上找点F,使AE平分∠BEF
操作如下:
第一步:找格点M,连接AM使AM AE,写出M的坐标为________
第二步:找格点G,连接EG,使AG平分∠MAE,写出点G的坐标为_______;
第三步:AG交x轴于点F,连接EF,则AE平分∠BEF.
请你按步骤完成作图,并说明理由.
用无刻度的直尺作图(辅助线请画虚线)
(1)如图1,在 ABCD中画一条直线平分周长;
(2)如图2,在O中,AB为O内的一条弦,D为优弧AB的中点,C为优弧AB的一动点,画出∠ACB的平分线;
(3)如图3,在正方形ABCD中,E为CB上的任意一点,在AB上截取一点F,使得BF=BE.
如图,在下列10×10的风格中,横、纵坐标均为整点的数叫做格点,例如A(-2,-2),B(5,-3),C(1,2)都是格点.
(1)∠ACB的大小为________
(2)要求在下图中仅用无刻度的直尺作图:以A为中心,取旋转角等于∠BAC.
把ABC逆时针旋转,得到ABC,其中点C和点B的对应点分别为点C和B,操作步骤如下:
第一步:延长AC到格点B1,使得AB1=AB;
第二步:延长BC到格点E,使得CE=CB,连接AE;
第三步:取格点F,连接FB1交AE于点C1,则AB1C1即为所示.
请你按步骤完成作图,并直接写出B1、E、F三点的坐标.
横、纵坐标均为整数的点称为格点,如图,ABC的三个顶点A(2,1),B(6,3),C(3,3)均为格点,AB上的点D(4,2)也为格点,用无刻度的直尺作图;
将线段AD绕点A顺时针旋转90°,得到线段AE,写出格点E的坐标;
将线段AE平移至线段CM,使点A与点C重合,直接写出格点M的坐标;
画出线段AC关于CM对称的线段CH,保留作图痕迹.
如图是由边长相等的小正方形组成的网格,以下各衅中点A、B、C、D都在格点上,
在图1中,PC:PB=________;
利用网格和无刻度的直尺作图,保留痕迹,不写作法.
如图2,在AB上找点P,使得AP:PB=1:3;
如图3,在ABC中内找一点G,连接GA、GB、GC,将ABC分成面积相等的三部分;
如图4,在ABC中,AB与网格线的交点为D,画点E,使DE AC.
以下各图均是由边长为1的小正方形组成的网格,图中的点A、B、C、D均在格点上,
在图1中,PA:PD=________ ;(填两数字之比)
利用网格和无刻度的直尺作图,保留痕迹,不写作法.
如图2,在线段AB上找一点P使
如图3,在线段BD上找一点P,使APB~CPD
请用无刻度的直尺作图.
在图1中,已知点E是正方形ABCD边AB的中点,画出CD的中点F;
图2是正方形ABCD,E是对角线BD上任意一点(BE>DE),以AE为边画一个菱形.
按要求作图,不要求写作法,但要保留作图痕迹.
(1)如图1,矩形ABCD的顶点A、D在圆上,B、C两点在圆心,已知圆心O请仅用无刻度的直尺作图,请作出直线l AD
(2)请仅用无刻度的直尺在下列图2和图3中按要求作图.(补上所作图开顶点字母)
1.图2是矩形ABCD,E、F分别是AB和AD的中点,以EF为边作一个菱形;
2.图4是矩形ABCD,E是对角线BD上任意一点(BE>DE),以AE为边作一个平行四边形.
已知正方形ABCD的边长为4个单位长度,点E是CD的中点,请仅用无刻度的直尺按下列要求作图(保留作图痕迹)
在图1中,将直线AC绕着正方形ABCD的中心顺时针旋转45°
在图2中,将直线AC向上平移1个单位长度.
如图平行四边形ABCD,E在AD边上,且DE=CD,仅用无刻度的直尺作图并保留作图痕迹,不写画法.
在图1中,来出∠C的角平分线;
在图2中,画出∠A的角平分线.
15.如图是边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点,在四边形ABDC中,
请你使用无刻度直尺作图,并保留作图痕迹.
(1)在直线BD上有一动点F,连接AF、FC,请作出点F使得(AF+FC)为最小值.
(2)在线段AB上有一点M,使S△ACM:S△BFM=4:1,请你画出点M的位置.
(3)延长FM、CD交于E,连接CM,请直接写出=________ ,S△CME=_______ .
16.如图,矩形ABCD与圆O交于点D,点A为圆O上一点,AB=2BC,请仅用无刻度的直尺,
分别按下列要求作图(保留作图痕迹)
(1)在图1中作出过点D的切线;
(2)在图2中作一个圆周角,使这个角的正切值为
17.在如图的网格中建立平面直角坐标系,△ABP的顶点坐标分别为A(0,3),B(1,0)P(3,2),仅用无刻度的直尺在给定网格中完成画图,画图过程中用虚线表示,并回答下列问题:
(1)在图1中,作线段CD,使P为线段CD与线段AB的位似中心,且满足
(2)在图2中,作出△PAB的外心M,并直接写出M的坐标______
(3)在图2中,作出△PAB的外接圆的切线PE.
如图,是由小正方形构成的6×6风格,每个小正方形的顶点叫做格点,圆P经过A、B两个格点,仅用无刻度的直尺在给定网格中按要求画图(画图过程用虚线表示,画图结果有实线表示)
(1)在图1中,圆P经过格点C,画圆心P,并画弦BD,使BD平分∠ABC
(2)在图2中,圆P经过格点E,F是圆P与网格线的交点,画圆心P,并画弦FG,使FG=FA.
扩展:1.圆P经过格点A,与格线交于点C,在圆上求作点D(不同于A),使CD=CA.
2.如图,圆P经过格点A,与格线交于点B,在圆上求作点E(不同于A,使AE=AB.
如图,已知A、B、C均在圆O上,请用无刻度的直尺作图,
(1)如图1,若点D是AC的中点,试画出∠B的平分线;
(2)如图2,若BD||AC,试画出∠ABC的平分线.
已知形ABCD的顶点A、D在圆上,B、C两点在圆内,请仅用无刻度的直尺作图.
(1)如图1,已知圆心O,请作出直线l AD
(2)如图2,未知圆心O,请作为直线l AD.
用无刻度的直尺作图,保留作图痕迹.
ABCD的边CD切⊙O于D
①在图1中CD上确定N点,使ON等分 ABCD的面积
②在如图2中,作CD边的高BH
ABCD的边CD与⊙O相切
①在图3中作OM CD于M;
②在图4中作CD边的垂线BH.
如图,在下列6×6的网格中,横、纵坐标均为整数的点叫做格点,例如A(0,3),B(5,3),C(1,5),D(3,4)都是格点,在网格中仅用无刻度的直尺作图,画图过程用虚线表示,画图结果用实线表示,并回答下列问题
直线写出ABC的形状;
画出点D关于AB的对称点E,并写出点E的坐标;
在线段AB上找一点F,连接F,使DF||AC;
在线段AB上确定一点M使得tan∠ACM=
23.如图,每个小正方形的边长都是1的方格纸中,有线段AC和EF,点A、C、E、F都在小正方形的顶点上.
(1)在方格纸中画出一个以线段AC为对角线的正方形ABCD,
所画的正方形的各顶点必须在小正方形的顶点上.
(2)在方格纸中以EF为腰画出等腰三角形EFM,点M在小正方形的顶点上,且MF=MC.
(3)在(1)、(2)的条件下,连接MA,请直接写出线段MA的长.
24.如图,在含有60°角的5×6菱形网格中,我们把顶点都在格点上的多边形称为格点多边形,
A,B均在格点上,按下面要求画出格点多边形.
(1)在图1中画出一个等腰三角形ABC.
(2)在图2中画出一个菱形APBQ.
参考答案
(1)AB=5 (2)原理:ABDPAE可得ABP为等腰直角三角形,故∠ABP=45°
(1)BC= (2)原理:12345原理
原理:连接BE、CE交点即为所示的点P,证明:ACDAEB,可∠ADC=∠ABE,∠BPD=180°-∠BDP-∠DBA-∠ABP=180°-∠BDP-60°-∠ADC=60°,故∠BPC=120°
原理:平行边形、等腰三角形的性质,共圆的性质;
原理:弦图垂直的性质、同余
原理:平行四边形、圆、正方形的性质
∠BAC=90°,B1(3,3),E(-3,5),F(-4,2)
E(3,-1),M(4,1)原理:全等,平移.
1:2
3:1
原理:平行四边形、矩形的对称性
原理:正方形的性质
原理:角平分与平行、等腰、中心对称图形
,
原理:圆与矩形的性质
原理:垂直平分线、位似、成比例线段
原理:圆的性质
扩展:
原理:垂径定理
20.原理:垂直径定理、矩形的性质
21.原理:矩形的性质、圆的性质、平行线分线段成比例
22.原理:平行线分线段成比例
23.原理:垂直平分线的性质、弦图性质
24.原理:全等及菱形的性质
同课章节目录
