人教版七数学年级下册10.1统计调查2课件(19张ppt)
文档属性
| 名称 | 人教版七数学年级下册10.1统计调查2课件(19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 589.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 21:51:23 | ||
图片预览






文档简介
(共19张PPT)
人教版数学七年级
10.1 统计调查 (2)
上节回顾
问题情境:
妈妈:“儿子,再帮妈妈买鸡蛋去。”
妈妈:“这次注意点,上次你买的鸡蛋有好几个是坏的。”
儿子高兴地跑回来。
儿子:“妈妈,这次的鸡蛋全是好的,我每个都打开看过了。”
妈妈:“啊!”
问:在这则笑话中,儿子采用的是什么调查?
这种调查好不好?还可采用什么样的调查方法呢?
10.1 统计调查(2)
学习目标
(1)理解抽样调查的概念,能够区分抽样调查和全面调查,能对数据进行简单的收集整理。
(2)理解总体、个体、样本、样本容量等概念。
(3)理解随机抽样的合理性。
问题2:某校有2 000名学生,要想了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,怎样进行调查?
讨论1:
(1)这道题与上节课的问题1有什么区别?
(2)采用全面调查方法对全校学生逐个进行调查可行吗?你认为是否有这个必要?能否找到一种更简便的调查方法?
探究新知
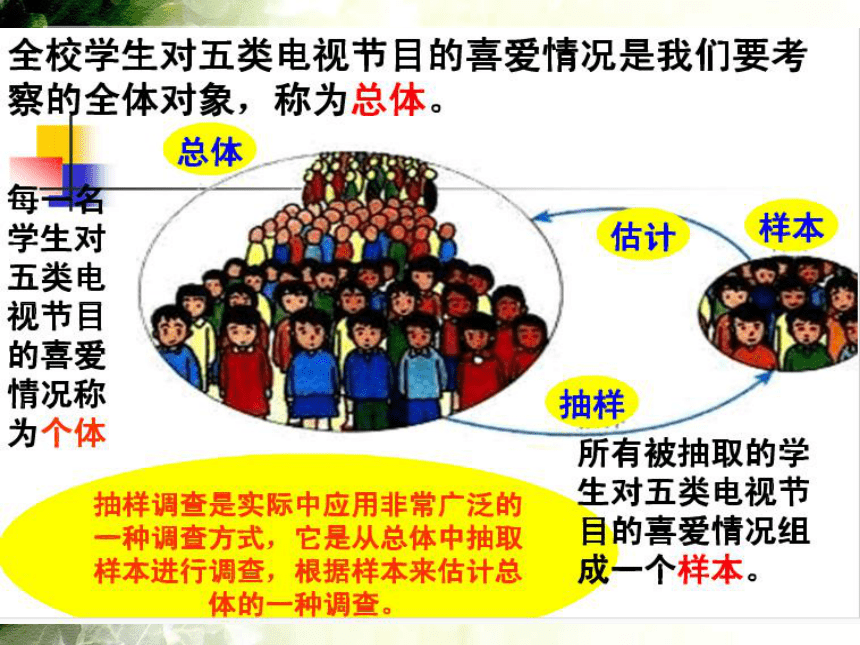
抽样调查:是这样一种方法,它只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况.要考察的全体对象称为总体,组成总体的每一个考察对象称为个体,被抽取的那些个体组成一个样本.
讨论2:抽取多少名学生进行调查比较合适?被调查的学生又如何抽取呢?
如果抽取的学生人数很少,那么样本就不能很好地反映总体的情况.如果抽取的学生人数很多,必然花费大量的时间精力,达不到省时省力的目的.因此抽取的学生数目要适当.样本中个体的数目称为样本容量.本问题可以抽取100名同学,即样本容量为100.
讨论2:抽取多少名学生进行调查比较合适?被调查的学生又如何抽取呢?
为了使样本能较好地反映总体情况,除了有合适的样本容量外,抽取时还要尽量使每一个个体有相等的机会被抽到.例如,可以在2 000名学生的注册学号中,随意抽取100个学号,调查这些学号对应的100名学生.
归纳:
全面调查和抽样调查是收集数据的两种方式.全面调查收集到的数据全面、准确,但一般花费多、耗时长,而且某些调查不宜用全面调查.抽样调查具有花费少、省时的特点,但抽取的样本是否具有代表性,直接关系到对总体估计的准确程度.
讨论3:从表10-2中可以看出什么信
息?
从表格中可以看出,喜爱娱乐节目的学生最多,为38%,据此可以估计这个学校中,喜欢娱乐节目的最多,约为38%左右.类似地,可以估计这个学校的学生喜爱其他节目的百分比.
讨论3:你可以用条形图和扇形图来
描述上述表格中的数据吗?
条形图 扇形图
归纳:上面抽取样本的过程中,总体中每一个个体都有相等的机会被抽到,像这样的抽样方法叫简单随机抽样.
(1)当调查的对象个数较少,调查容易进行
时,我们一般采用全面调查的方式进行。
(2)当调查的结果对调查对象具有破坏性时,
或者会产生一定的危害性时,我们通常采
用抽样调查的方式进行调查。
(3)当调查对象的个数较多,调查不易进行
时,我们常采用抽样调查的方式进行调查。
(4)当调查的结果有特别要求时,或调查的结
果有特殊意义时,如国家的人口普查,我们
仍须采用全面调查的方式进行。
注意:在抽样调查中抽取的样本要具有代表性。
归纳:
例题讲解
例1、为了了解某校七年级400名学生的期中数学成绩的情况,从中抽取了50名学生的数学成绩进行分析。在这个问题中,
总体是▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁
个体是▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁
样本是▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁
样本容量是▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁
巩固新知
1、为了解全校同学的平均身高,小明调查了座位在自己旁边的3名同学,把他们的身高的平均值作为全校同学平均身高的估计
(1)小明的调查是抽样调查吗?
(2)这个调查结果能较好的反应总体情况吗?如果不能请说明理由。
2、一次调查中,哪些适宜全面调查,哪些适宜抽样调查?
(1)调查某批次汽车的抗击能力;
(2)了解某班学生的身高情况;
(3)调查春节联欢晚会的收视率;
(4)选出某校短跑最快的学生参加全市比赛。
学以致用:练一练
1.要调查下面几个问题,你认为应该作全面调查
还是抽样调查:
(1)调查我们班所有同学的体重情况
(2)调查市场上五色冰淇淋的色素含量是否符合国家标准;
(3)检测某城市的空气质量;
(4)调查某村所有家庭的年收入;
(5)调查灵山县初一年级的作业量情况;
(6)调查钦州市市早稻亩产量.
抽样调查
全面调查
抽样调查
全面调查
抽样调查
抽样调查
小结
数据的收集:调查问卷;
数据的整理:表格;
数据的描述:条形图、扇形图;
基本概念: 抽样调查、总体、个体、样
本、样本容量、随机抽样调
查
作业:P 159--160
3、4、8、11
人教版数学七年级
10.1 统计调查 (2)
上节回顾
问题情境:
妈妈:“儿子,再帮妈妈买鸡蛋去。”
妈妈:“这次注意点,上次你买的鸡蛋有好几个是坏的。”
儿子高兴地跑回来。
儿子:“妈妈,这次的鸡蛋全是好的,我每个都打开看过了。”
妈妈:“啊!”
问:在这则笑话中,儿子采用的是什么调查?
这种调查好不好?还可采用什么样的调查方法呢?
10.1 统计调查(2)
学习目标
(1)理解抽样调查的概念,能够区分抽样调查和全面调查,能对数据进行简单的收集整理。
(2)理解总体、个体、样本、样本容量等概念。
(3)理解随机抽样的合理性。
问题2:某校有2 000名学生,要想了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,怎样进行调查?
讨论1:
(1)这道题与上节课的问题1有什么区别?
(2)采用全面调查方法对全校学生逐个进行调查可行吗?你认为是否有这个必要?能否找到一种更简便的调查方法?
探究新知
抽样调查:是这样一种方法,它只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况.要考察的全体对象称为总体,组成总体的每一个考察对象称为个体,被抽取的那些个体组成一个样本.
讨论2:抽取多少名学生进行调查比较合适?被调查的学生又如何抽取呢?
如果抽取的学生人数很少,那么样本就不能很好地反映总体的情况.如果抽取的学生人数很多,必然花费大量的时间精力,达不到省时省力的目的.因此抽取的学生数目要适当.样本中个体的数目称为样本容量.本问题可以抽取100名同学,即样本容量为100.
讨论2:抽取多少名学生进行调查比较合适?被调查的学生又如何抽取呢?
为了使样本能较好地反映总体情况,除了有合适的样本容量外,抽取时还要尽量使每一个个体有相等的机会被抽到.例如,可以在2 000名学生的注册学号中,随意抽取100个学号,调查这些学号对应的100名学生.
归纳:
全面调查和抽样调查是收集数据的两种方式.全面调查收集到的数据全面、准确,但一般花费多、耗时长,而且某些调查不宜用全面调查.抽样调查具有花费少、省时的特点,但抽取的样本是否具有代表性,直接关系到对总体估计的准确程度.
讨论3:从表10-2中可以看出什么信
息?
从表格中可以看出,喜爱娱乐节目的学生最多,为38%,据此可以估计这个学校中,喜欢娱乐节目的最多,约为38%左右.类似地,可以估计这个学校的学生喜爱其他节目的百分比.
讨论3:你可以用条形图和扇形图来
描述上述表格中的数据吗?
条形图 扇形图
归纳:上面抽取样本的过程中,总体中每一个个体都有相等的机会被抽到,像这样的抽样方法叫简单随机抽样.
(1)当调查的对象个数较少,调查容易进行
时,我们一般采用全面调查的方式进行。
(2)当调查的结果对调查对象具有破坏性时,
或者会产生一定的危害性时,我们通常采
用抽样调查的方式进行调查。
(3)当调查对象的个数较多,调查不易进行
时,我们常采用抽样调查的方式进行调查。
(4)当调查的结果有特别要求时,或调查的结
果有特殊意义时,如国家的人口普查,我们
仍须采用全面调查的方式进行。
注意:在抽样调查中抽取的样本要具有代表性。
归纳:
例题讲解
例1、为了了解某校七年级400名学生的期中数学成绩的情况,从中抽取了50名学生的数学成绩进行分析。在这个问题中,
总体是▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁
个体是▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁
样本是▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁
样本容量是▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁
巩固新知
1、为了解全校同学的平均身高,小明调查了座位在自己旁边的3名同学,把他们的身高的平均值作为全校同学平均身高的估计
(1)小明的调查是抽样调查吗?
(2)这个调查结果能较好的反应总体情况吗?如果不能请说明理由。
2、一次调查中,哪些适宜全面调查,哪些适宜抽样调查?
(1)调查某批次汽车的抗击能力;
(2)了解某班学生的身高情况;
(3)调查春节联欢晚会的收视率;
(4)选出某校短跑最快的学生参加全市比赛。
学以致用:练一练
1.要调查下面几个问题,你认为应该作全面调查
还是抽样调查:
(1)调查我们班所有同学的体重情况
(2)调查市场上五色冰淇淋的色素含量是否符合国家标准;
(3)检测某城市的空气质量;
(4)调查某村所有家庭的年收入;
(5)调查灵山县初一年级的作业量情况;
(6)调查钦州市市早稻亩产量.
抽样调查
全面调查
抽样调查
全面调查
抽样调查
抽样调查
小结
数据的收集:调查问卷;
数据的整理:表格;
数据的描述:条形图、扇形图;
基本概念: 抽样调查、总体、个体、样
本、样本容量、随机抽样调
查
作业:P 159--160
3、4、8、11
