6.1分类加法计数原理与分步乘法计数原理 同步练习(Word版含解析)
文档属性
| 名称 | 6.1分类加法计数原理与分步乘法计数原理 同步练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 189.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 08:41:36 | ||
图片预览




文档简介
人教A版(2019)选择性必修第三册 6.1分类加法计数原理与分步乘法计数原理
一、单选题
1.有3名防控新冠肺炎疫情的志愿者,每人从2个不同的社区中选择1个进行服务,则不同的选择方法共有
( )
A.12种 B.9种 C.8种 D.6种
2.立德幼儿园王老师和李老师给小朋友发水果.王老师的果篮里有草莓,苹果,芒果3种水果.李老师的果篮里有苹果,櫻桃,香蕉,猕猴桃4种水果.小华可以在两个老师的果篮里分别选一个水果.小华拿到两种不同的水果的情况有( ).
A.7种 B.6种 C.12种 D.11种
3.某同学从3本不同的哲学图书 4本不同的自然科学图书 2本不同的社会科学图书中任选1本阅读,则不同的选法共有( )
A.24种 B.12种 C.9种 D.3种
4.某日,从赣州到南昌的火车共有10个车次,飞机共有2个航班,长途汽车共有12个班次,若该日甲只选择这3种交通工具中的一种,则甲从赣州到南昌共有( )
A.12种选法 B.24种选法
C.22种选法 D.14种选法
5.7个人排成一排准备照一张合影,其中甲、乙要求相邻,丙、丁要求分开,则不同的排法有( )
A.480种 B.720种 C.960种 D.1200种
6.将数字1,2,3,4填入标号为1,2,3,4的四个方格里,每格填一个数,则每个方格的标号与所填数字均不相同的填法有( )
A.6种 B.9种 C.11种 D.23种
7.数学中有回文数,如343,12521等.两位数的回文数有11,22,33,…,99,共9个,则在三位数的回文数中偶数的个数是( )
A.40 B.30 C.20 D.10
8.作家马伯庸的小说《长安十二时辰》中,靖安司通过长安城内的望楼传递信息.如图所示是望楼传递信息的一种方式,在九宫格中,每个小方格可以在白色和紫色(此处以阴影代表紫色)之间变换,从而一共可以有512种不同的颜色组合,即代表512种不同的信息.现要求每一行、每一列上有且只有1个紫色小方格(如图所示即满足要求),则一共可以传递的不同信息种数是( )
A.14 B.12 C.9 D.6
9.用红,黄,蓝,绿,黑这5种颜色随机给如图所示的四块三角形区域涂色,则“在任意两个有公共边的三角形所涂颜色不同”的概率为( )
A. B. C. D.
10.天河区某校开展学农活动时进行劳动技能比赛,通过初选,选出甲 乙 丙 丁 戊共5名同学进行决赛,决出第1名到第5名的名次.甲和乙去询问成绩,回答者对甲说“很遗憾,你和乙都未拿到冠军”;对乙说“你当然不是最差的”,试从这个回答中分析这5人的名次排列顺序可能出现的种类有( )
A.54种 B.60种 C.72种 D.96种
11.如图,用四种不同的颜色给图中的A,B,C,D,E,F,G七个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法有( )
A.192种 B.336种 C.600种 D.624种
12.集合,,以为定义域,为值域的函数的个数为( )
A.60 B.150 C.540 D.
二、填空题
13.如图,用四种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法的种数为______(用数字作答)
14.中国古典数学的代表作有《算数书》《九章算术》《周髀算经》《孙子算经》等.学校图书馆计划将这四本书借给名学生阅读,要求每人至少读一本,则不同的借阅方式有_______种(用数字作答).
15.将一张面值1元的人民币全部换成面值1角,2角和5角的硬币,则换法总数为______.
16.一排有10盏灯,如果用灯亮表示数1,用灯不亮表示数0,每一种亮灯方式代表一个数据,如:0010100101表示一个数据,那么这10盏灯可以表示的数据个数是___________.
17.作家马伯庸小说《长安十二时辰》中,靖安司通过长安城内的望楼传递信息.同名改编电视剧中,望楼传递信息的方式有一种如下:如图所示,在九宫格中,每个小方格可以在白色和紫色(此处以阴影代表紫色)之间变换,从而一共可以有512种不同的颜色组合,即代表512种不同的信息.现要求每一行、每一列上都有且只有1个紫色小方格(如图所示即满足要求).则一共可以传递______种信息.(用数字作答)
三、解答题
18.在10张奖券中有3张可以中奖,求从中抽出4张,至少有1张中奖的抽法的种数.
19.2160有多少个不同的正因数?
20.从5名同学中选出正、副组长各1名,有多少种不同的选法?
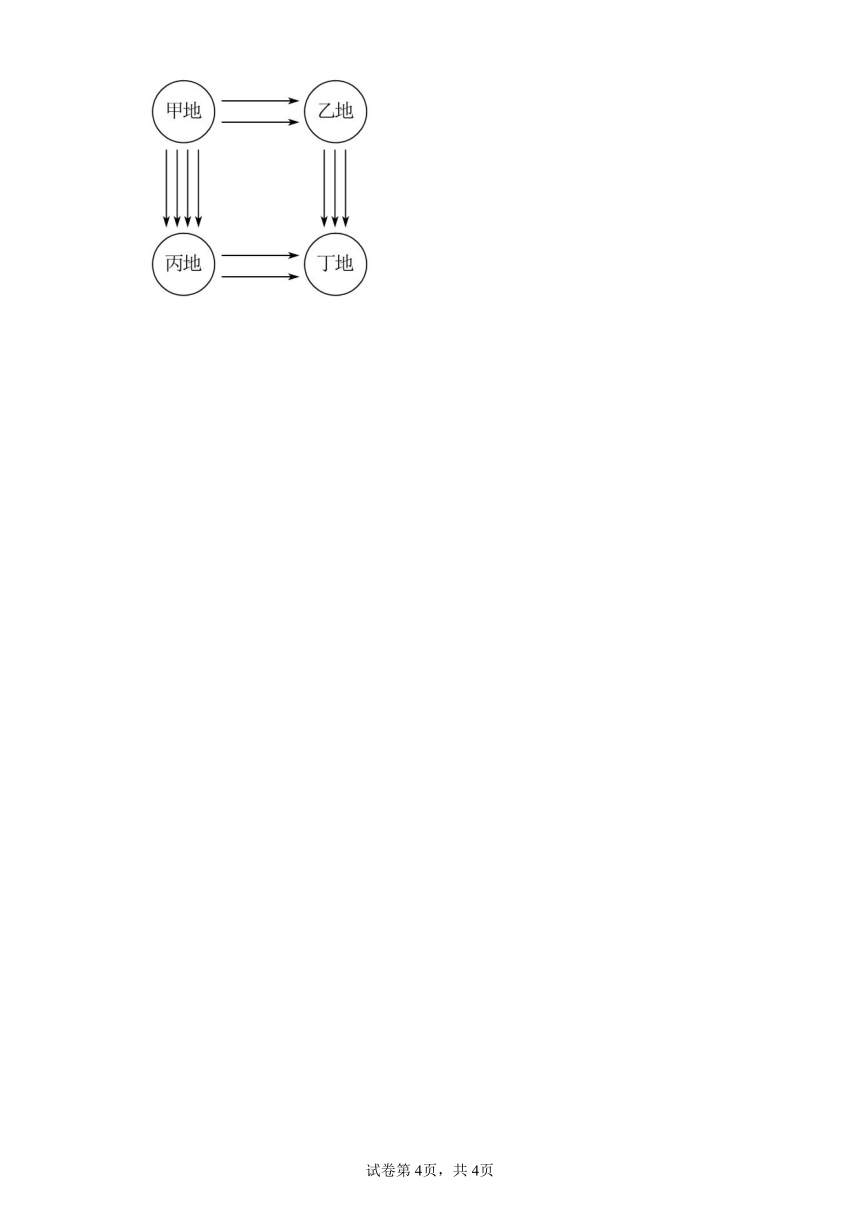
21.如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路,从丙地到丁地有2条路.从甲地到丁地共有多少条不同的路线?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
根据分步计数原理可求.
【详解】
每名防控新冠肺炎疫情的志愿者都有2种不同的选择方法,根据分步计数原理可知,不同的选择方法共有(种).
故选:C.
2.D
结合分类、分步计数原理计算出正确答案.
【详解】
王老师有3种水果,李老师有4种水果.其中苹果是重复的.所以应该先分类后分步.
第一类,如果小华在王老师那里拿到苹果,
那么在李老师那里只能从剩下3种水果中拿,共有(种)情况.
第二类,如果小华在王老师那里拿到的不是苹果,那么就有2种情况,
在李老师那里有4种情况,共有(种)情况.
根据分类加法计数原理,得小华拿到两种不同水果总共有(种)情况.
故选:D
3.C
利用分类加法计数原理直接求出答案即可.
【详解】
解:由分类加法计数原理知,不同的选法种数为.
故选:C.
4.B
根据计数原理的加法法则可得选项.
【详解】
由计数原理的加法法则可得,甲从赣州到南昌共有10+2+12=24种选法.
故选:B.
5.C
甲、乙要求相邻,则把甲和乙看成一个元素,与除去丙和丁以外的共4个元素进行全排列,其中甲和乙之间还有一个排列,根据丙和丁不相邻,把形成的五个空选两个排列丙和丁.得到结果.
【详解】
解:由题意知,
甲、乙要求相邻,则把甲和乙看成一个元素,
与除去丙和丁以外的共4个元素进行全排列,其中甲和乙之间还有一个排列,
把形成的五个空选两个排列丙和丁,
根据分步计数原理知共有A44A22A52=960种.
故选:C.
6.B
第一步,把1填入方格中,第二步,把被填入方格的对应数字填入其它三个方格,然后填余下的两个数字,即可求解.
【详解】
先把1填入方格中,符合条件的有3种方法,
第二步把被填入方格的对应数字填入其它三个方格,又有三种方法;
第三步填余下的两个数字,只有一种填法,共有3×3×1=9种填法,
故选:B.
7.A
首先安排末(首)位,再考虑中间位置,按照分步乘法计数原理计算可得;
【详解】
解:由题意,若三位数的回文数是偶数,则末(首)位可能为2,4,6,8.如果末(首)位为2,中间一位数有10种可能,同理可得,如果末(首)位为4或6或8,中间一位数均有10种可能,所以在三位数的回文数总偶数的个数是.
故选:A
8.D
由分步乘法原理求传递的不同信息种数.
【详解】
根据每行中紫色小方格的位置,可分三步:第一步,在第一行中,有且只有1个紫色小方格,有3种情况;第二步,在第二行的3个方格中,要求每列有且只有1个紫色小方格,则第二行有2种情况;第三步,在第三行,只有1种情况,则一共可以传递的信息种数是,
故选:D.
9.A
求出所有涂色方法数为,再求出在任意两个有公共边的三角形所涂颜色不同的方法数,可先从中间一个三角形涂色,然后再涂其他三个三角形.
【详解】
5种颜色随机给如图所示的四块三角形区域涂色方法数为,
有公共边的三角形为同色,先考虑中间一块涂色有5种方法,其他三个三角形在剩下的4色中任意涂色均可,方法为,
所以所求概率为.
故选:A.
10.A
甲乙不是第一名且乙不是最后一名,乙的限制最多,先排乙,可以是第二,三,四名3种情况,再排甲,也有3种情况,余下的问题是三个元素在三个位置全排列,根据分步计数原理求解即可.
【详解】
由题意,甲乙不是第一名且乙不是最后一名,乙的限制最多,故先排乙,有3种情况,
再排甲,也有3种情况,余下3人有种情况,
利用分步相乘计数原理知有种情况
故选:A.
思路点睛:解决排列组合问题的一般过程:
(1)认真审题弄清楚要做什么事情;
(2)要做的事情是需要分步还是分类,还是分步分类同时进行,确定分多少步及多少类;
(3)确定每一步或每一类是排列(有序)问题还是组合(无序)问题,元素总数是多少及取出多少元素.
11.C
由题意,点E,F,G分别有4,3,2种涂法,再分当A与F相同、A与G相同和A既不同于F又不同于G,三种情况讨论,进而求解.
【详解】
由题意,点E,F,G分别有4,3,2种涂法,
(1)当A与F相同时,A有1种涂色方法,此时B有2种涂色方法,
①若C与F相同,则C有1种涂色方法,此时D有3种涂色方法;
②若C与F不同,则D有2种涂色方法.
故此时共有种涂色方法.
(2)当A与G相同时,A有1种涂色方法,
①若C与F相同,则C有1种涂色方法,此时B有2种涂色方法,D有2种涂色方法;
②若C与F不同,则C有2种涂色方法,此时B有2种涂色方法,D有1种涂色方法.
故此时共有种涂色方法.
(3)当A既不同于F又不同于G时,A有1种涂色方法.
①若B与F相同,则C与A相同时,D有2种涂色方法,C与A不同时,C和D均只有1种涂色方法;
②若B与F不同,则B有1种涂色方法,
(i)若C与F相同,则C有1种涂色方法,此时D有2种涂色方法;
(ii)若C与F不同,则必与A相同,C有1种涂色方法,此时D有2种涂色方法.
故此时共有种涂色方法.
综上,共有种涂色方法.
故选:C.
利用两个计数原理解题的策:
1、利用分类计数原理解题分类时应注意完成这件事情的任何一种方法必须属于某一类,并且分步属于不同种类的两种方法是不同的方法,不能重复,分类时除了不能交叉重复外,还不能有遗漏;
2、利用分步计数原理解题时要注意按事件发生的过程合理分步,即分步时有先有后顺序的,并且分步必须满足:完成一件事的各个步骤是相互依存的,只有各个步骤都完成了,才算完成这件事,分步必须满足两个条件:一是各步骤相互独立,互不干扰;二是步与步之间确保连续,逐步完成.
12.B
求以为定义域,为值域的函数的个数相当于把5个不同的球放入3个不同的盒子中,且盒子不能空的放法,先把5个不同的球分成3组,然后放入3个盒子即可
【详解】
由题意可知求以为定义域,为值域的函数的个数相当于把5个不同的球放入3个不同的盒子中,且盒子不能空的放法,
先将5个不同的球分成3组,不同的分法有种,然后每个盒子中放一组即可,
所以共有种,
所以以为定义域,为值域的函数的个数为150,
故选:B
13.48
由已知按区域分四步,然后给,,,区域分步选择颜色,由此即可求解.
【详解】
解:由已知按区域分四步:第一步区域有4种选择,第二步区域有3种选择,
第三步区域有2种选择,第四步区域也有2种选择,
则由分步计数原理可得共有种,
故答案为:48.
14.36
根据题意,分2步进行分析:
①从4本书中选出2本,分配给三人中的1人;②剩下的2本安排给剩下的2人;
由分步计数原理可得答案.
【详解】
根据题意,分2步进行分析:
①从4本书中选出2本,分配给三人中的1人,有种;
②剩下的2本安排给剩下的2人,有种;
则有18×2=36种.
故答案为:36.
15.10
设1角硬币有x枚,2角硬币有y枚,5角硬币有z枚,构造三元一次方程,然后利用列举法得到所有可能的情况,可得答案.
【详解】
设1角硬币有x枚,2角硬币有y枚,5角硬币有z枚,则.
满足方程的解有:
;
;
;
;
;
;
;
;
;
;
共十种不同情况.
故答案为:10 .
16.1024
由于每盏灯有两种情况,所以由分步乘法原可求得结果
【详解】
因为用灯亮表示数1,用灯不亮表示数0,每一种亮灯方式代表一个数据,
所以由乘法分步原理可知这10盏灯可以表示的数据个数为个,
故答案为:1024
17.6
由题意,分3步依次分析三行方格的可能情况数目,由分步计数原理计算可得答案
【详解】
解:根据题意,分3步分析:
第一步,在每行中,有且只有1个紫色小方格,有3 种情况,
第二步,在第二行的3个方格中,要求每列上都有且只有一个紫色小方格,则第二行有2种情况,
第三步,在第三行,只有1种情况,
则有种情况,
故答案为:6
18.175(种)
分有1张、2张、3张中奖,三种情况讨论,即可
【详解】
有3张可以中奖的奖券,7张不能中奖的奖券,分三类:
第一类:有1张中奖的抽法是种;
第二类:有2张中奖的抽法是种;
第三类:有3张中奖的抽法是种;
因此,共有(种).
19.40
对2160分解因数,转化2160的正因数,结合参数的取值及分步乘法计数原理即可得解.
【详解】
由题意,,
则2160的正因数,
因为可取0,1,2,3,4;可取0,1;可取0,1,2,3;
所以2160有个不同的正因数.
20.20种选法
从5人中依次选出正、副组长,由分步乘法计数原理即可得解.
【详解】
先从5人中选出一名组长,共有5种选法,
再从剩下的4人中选出一名副组长,共有4种选法,
所以从5名同学中选出正、副组长各1名,共有种选法.
21.14种
按照甲地经乙地到丁地、甲地经丙地到丁地分类,结合分类加法、分步乘法计数原理即可得解.
【详解】
如果由甲地经乙地到丁地,则有种不同的路线;
如果由甲地经丙地到丁地,则有种不同的路线;
因此,从甲地到丁地共有种不同的路线.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.有3名防控新冠肺炎疫情的志愿者,每人从2个不同的社区中选择1个进行服务,则不同的选择方法共有
( )
A.12种 B.9种 C.8种 D.6种
2.立德幼儿园王老师和李老师给小朋友发水果.王老师的果篮里有草莓,苹果,芒果3种水果.李老师的果篮里有苹果,櫻桃,香蕉,猕猴桃4种水果.小华可以在两个老师的果篮里分别选一个水果.小华拿到两种不同的水果的情况有( ).
A.7种 B.6种 C.12种 D.11种
3.某同学从3本不同的哲学图书 4本不同的自然科学图书 2本不同的社会科学图书中任选1本阅读,则不同的选法共有( )
A.24种 B.12种 C.9种 D.3种
4.某日,从赣州到南昌的火车共有10个车次,飞机共有2个航班,长途汽车共有12个班次,若该日甲只选择这3种交通工具中的一种,则甲从赣州到南昌共有( )
A.12种选法 B.24种选法
C.22种选法 D.14种选法
5.7个人排成一排准备照一张合影,其中甲、乙要求相邻,丙、丁要求分开,则不同的排法有( )
A.480种 B.720种 C.960种 D.1200种
6.将数字1,2,3,4填入标号为1,2,3,4的四个方格里,每格填一个数,则每个方格的标号与所填数字均不相同的填法有( )
A.6种 B.9种 C.11种 D.23种
7.数学中有回文数,如343,12521等.两位数的回文数有11,22,33,…,99,共9个,则在三位数的回文数中偶数的个数是( )
A.40 B.30 C.20 D.10
8.作家马伯庸的小说《长安十二时辰》中,靖安司通过长安城内的望楼传递信息.如图所示是望楼传递信息的一种方式,在九宫格中,每个小方格可以在白色和紫色(此处以阴影代表紫色)之间变换,从而一共可以有512种不同的颜色组合,即代表512种不同的信息.现要求每一行、每一列上有且只有1个紫色小方格(如图所示即满足要求),则一共可以传递的不同信息种数是( )
A.14 B.12 C.9 D.6
9.用红,黄,蓝,绿,黑这5种颜色随机给如图所示的四块三角形区域涂色,则“在任意两个有公共边的三角形所涂颜色不同”的概率为( )
A. B. C. D.
10.天河区某校开展学农活动时进行劳动技能比赛,通过初选,选出甲 乙 丙 丁 戊共5名同学进行决赛,决出第1名到第5名的名次.甲和乙去询问成绩,回答者对甲说“很遗憾,你和乙都未拿到冠军”;对乙说“你当然不是最差的”,试从这个回答中分析这5人的名次排列顺序可能出现的种类有( )
A.54种 B.60种 C.72种 D.96种
11.如图,用四种不同的颜色给图中的A,B,C,D,E,F,G七个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法有( )
A.192种 B.336种 C.600种 D.624种
12.集合,,以为定义域,为值域的函数的个数为( )
A.60 B.150 C.540 D.
二、填空题
13.如图,用四种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法的种数为______(用数字作答)
14.中国古典数学的代表作有《算数书》《九章算术》《周髀算经》《孙子算经》等.学校图书馆计划将这四本书借给名学生阅读,要求每人至少读一本,则不同的借阅方式有_______种(用数字作答).
15.将一张面值1元的人民币全部换成面值1角,2角和5角的硬币,则换法总数为______.
16.一排有10盏灯,如果用灯亮表示数1,用灯不亮表示数0,每一种亮灯方式代表一个数据,如:0010100101表示一个数据,那么这10盏灯可以表示的数据个数是___________.
17.作家马伯庸小说《长安十二时辰》中,靖安司通过长安城内的望楼传递信息.同名改编电视剧中,望楼传递信息的方式有一种如下:如图所示,在九宫格中,每个小方格可以在白色和紫色(此处以阴影代表紫色)之间变换,从而一共可以有512种不同的颜色组合,即代表512种不同的信息.现要求每一行、每一列上都有且只有1个紫色小方格(如图所示即满足要求).则一共可以传递______种信息.(用数字作答)
三、解答题
18.在10张奖券中有3张可以中奖,求从中抽出4张,至少有1张中奖的抽法的种数.
19.2160有多少个不同的正因数?
20.从5名同学中选出正、副组长各1名,有多少种不同的选法?
21.如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路,从丙地到丁地有2条路.从甲地到丁地共有多少条不同的路线?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
根据分步计数原理可求.
【详解】
每名防控新冠肺炎疫情的志愿者都有2种不同的选择方法,根据分步计数原理可知,不同的选择方法共有(种).
故选:C.
2.D
结合分类、分步计数原理计算出正确答案.
【详解】
王老师有3种水果,李老师有4种水果.其中苹果是重复的.所以应该先分类后分步.
第一类,如果小华在王老师那里拿到苹果,
那么在李老师那里只能从剩下3种水果中拿,共有(种)情况.
第二类,如果小华在王老师那里拿到的不是苹果,那么就有2种情况,
在李老师那里有4种情况,共有(种)情况.
根据分类加法计数原理,得小华拿到两种不同水果总共有(种)情况.
故选:D
3.C
利用分类加法计数原理直接求出答案即可.
【详解】
解:由分类加法计数原理知,不同的选法种数为.
故选:C.
4.B
根据计数原理的加法法则可得选项.
【详解】
由计数原理的加法法则可得,甲从赣州到南昌共有10+2+12=24种选法.
故选:B.
5.C
甲、乙要求相邻,则把甲和乙看成一个元素,与除去丙和丁以外的共4个元素进行全排列,其中甲和乙之间还有一个排列,根据丙和丁不相邻,把形成的五个空选两个排列丙和丁.得到结果.
【详解】
解:由题意知,
甲、乙要求相邻,则把甲和乙看成一个元素,
与除去丙和丁以外的共4个元素进行全排列,其中甲和乙之间还有一个排列,
把形成的五个空选两个排列丙和丁,
根据分步计数原理知共有A44A22A52=960种.
故选:C.
6.B
第一步,把1填入方格中,第二步,把被填入方格的对应数字填入其它三个方格,然后填余下的两个数字,即可求解.
【详解】
先把1填入方格中,符合条件的有3种方法,
第二步把被填入方格的对应数字填入其它三个方格,又有三种方法;
第三步填余下的两个数字,只有一种填法,共有3×3×1=9种填法,
故选:B.
7.A
首先安排末(首)位,再考虑中间位置,按照分步乘法计数原理计算可得;
【详解】
解:由题意,若三位数的回文数是偶数,则末(首)位可能为2,4,6,8.如果末(首)位为2,中间一位数有10种可能,同理可得,如果末(首)位为4或6或8,中间一位数均有10种可能,所以在三位数的回文数总偶数的个数是.
故选:A
8.D
由分步乘法原理求传递的不同信息种数.
【详解】
根据每行中紫色小方格的位置,可分三步:第一步,在第一行中,有且只有1个紫色小方格,有3种情况;第二步,在第二行的3个方格中,要求每列有且只有1个紫色小方格,则第二行有2种情况;第三步,在第三行,只有1种情况,则一共可以传递的信息种数是,
故选:D.
9.A
求出所有涂色方法数为,再求出在任意两个有公共边的三角形所涂颜色不同的方法数,可先从中间一个三角形涂色,然后再涂其他三个三角形.
【详解】
5种颜色随机给如图所示的四块三角形区域涂色方法数为,
有公共边的三角形为同色,先考虑中间一块涂色有5种方法,其他三个三角形在剩下的4色中任意涂色均可,方法为,
所以所求概率为.
故选:A.
10.A
甲乙不是第一名且乙不是最后一名,乙的限制最多,先排乙,可以是第二,三,四名3种情况,再排甲,也有3种情况,余下的问题是三个元素在三个位置全排列,根据分步计数原理求解即可.
【详解】
由题意,甲乙不是第一名且乙不是最后一名,乙的限制最多,故先排乙,有3种情况,
再排甲,也有3种情况,余下3人有种情况,
利用分步相乘计数原理知有种情况
故选:A.
思路点睛:解决排列组合问题的一般过程:
(1)认真审题弄清楚要做什么事情;
(2)要做的事情是需要分步还是分类,还是分步分类同时进行,确定分多少步及多少类;
(3)确定每一步或每一类是排列(有序)问题还是组合(无序)问题,元素总数是多少及取出多少元素.
11.C
由题意,点E,F,G分别有4,3,2种涂法,再分当A与F相同、A与G相同和A既不同于F又不同于G,三种情况讨论,进而求解.
【详解】
由题意,点E,F,G分别有4,3,2种涂法,
(1)当A与F相同时,A有1种涂色方法,此时B有2种涂色方法,
①若C与F相同,则C有1种涂色方法,此时D有3种涂色方法;
②若C与F不同,则D有2种涂色方法.
故此时共有种涂色方法.
(2)当A与G相同时,A有1种涂色方法,
①若C与F相同,则C有1种涂色方法,此时B有2种涂色方法,D有2种涂色方法;
②若C与F不同,则C有2种涂色方法,此时B有2种涂色方法,D有1种涂色方法.
故此时共有种涂色方法.
(3)当A既不同于F又不同于G时,A有1种涂色方法.
①若B与F相同,则C与A相同时,D有2种涂色方法,C与A不同时,C和D均只有1种涂色方法;
②若B与F不同,则B有1种涂色方法,
(i)若C与F相同,则C有1种涂色方法,此时D有2种涂色方法;
(ii)若C与F不同,则必与A相同,C有1种涂色方法,此时D有2种涂色方法.
故此时共有种涂色方法.
综上,共有种涂色方法.
故选:C.
利用两个计数原理解题的策:
1、利用分类计数原理解题分类时应注意完成这件事情的任何一种方法必须属于某一类,并且分步属于不同种类的两种方法是不同的方法,不能重复,分类时除了不能交叉重复外,还不能有遗漏;
2、利用分步计数原理解题时要注意按事件发生的过程合理分步,即分步时有先有后顺序的,并且分步必须满足:完成一件事的各个步骤是相互依存的,只有各个步骤都完成了,才算完成这件事,分步必须满足两个条件:一是各步骤相互独立,互不干扰;二是步与步之间确保连续,逐步完成.
12.B
求以为定义域,为值域的函数的个数相当于把5个不同的球放入3个不同的盒子中,且盒子不能空的放法,先把5个不同的球分成3组,然后放入3个盒子即可
【详解】
由题意可知求以为定义域,为值域的函数的个数相当于把5个不同的球放入3个不同的盒子中,且盒子不能空的放法,
先将5个不同的球分成3组,不同的分法有种,然后每个盒子中放一组即可,
所以共有种,
所以以为定义域,为值域的函数的个数为150,
故选:B
13.48
由已知按区域分四步,然后给,,,区域分步选择颜色,由此即可求解.
【详解】
解:由已知按区域分四步:第一步区域有4种选择,第二步区域有3种选择,
第三步区域有2种选择,第四步区域也有2种选择,
则由分步计数原理可得共有种,
故答案为:48.
14.36
根据题意,分2步进行分析:
①从4本书中选出2本,分配给三人中的1人;②剩下的2本安排给剩下的2人;
由分步计数原理可得答案.
【详解】
根据题意,分2步进行分析:
①从4本书中选出2本,分配给三人中的1人,有种;
②剩下的2本安排给剩下的2人,有种;
则有18×2=36种.
故答案为:36.
15.10
设1角硬币有x枚,2角硬币有y枚,5角硬币有z枚,构造三元一次方程,然后利用列举法得到所有可能的情况,可得答案.
【详解】
设1角硬币有x枚,2角硬币有y枚,5角硬币有z枚,则.
满足方程的解有:
;
;
;
;
;
;
;
;
;
;
共十种不同情况.
故答案为:10 .
16.1024
由于每盏灯有两种情况,所以由分步乘法原可求得结果
【详解】
因为用灯亮表示数1,用灯不亮表示数0,每一种亮灯方式代表一个数据,
所以由乘法分步原理可知这10盏灯可以表示的数据个数为个,
故答案为:1024
17.6
由题意,分3步依次分析三行方格的可能情况数目,由分步计数原理计算可得答案
【详解】
解:根据题意,分3步分析:
第一步,在每行中,有且只有1个紫色小方格,有3 种情况,
第二步,在第二行的3个方格中,要求每列上都有且只有一个紫色小方格,则第二行有2种情况,
第三步,在第三行,只有1种情况,
则有种情况,
故答案为:6
18.175(种)
分有1张、2张、3张中奖,三种情况讨论,即可
【详解】
有3张可以中奖的奖券,7张不能中奖的奖券,分三类:
第一类:有1张中奖的抽法是种;
第二类:有2张中奖的抽法是种;
第三类:有3张中奖的抽法是种;
因此,共有(种).
19.40
对2160分解因数,转化2160的正因数,结合参数的取值及分步乘法计数原理即可得解.
【详解】
由题意,,
则2160的正因数,
因为可取0,1,2,3,4;可取0,1;可取0,1,2,3;
所以2160有个不同的正因数.
20.20种选法
从5人中依次选出正、副组长,由分步乘法计数原理即可得解.
【详解】
先从5人中选出一名组长,共有5种选法,
再从剩下的4人中选出一名副组长,共有4种选法,
所以从5名同学中选出正、副组长各1名,共有种选法.
21.14种
按照甲地经乙地到丁地、甲地经丙地到丁地分类,结合分类加法、分步乘法计数原理即可得解.
【详解】
如果由甲地经乙地到丁地,则有种不同的路线;
如果由甲地经丙地到丁地,则有种不同的路线;
因此,从甲地到丁地共有种不同的路线.
答案第1页,共2页
答案第1页,共2页
