7.4二项分布与超几何分布 同步练习(Word版含解析)
文档属性
| 名称 | 7.4二项分布与超几何分布 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 662.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 00:00:00 | ||
图片预览




文档简介
人教A版(2019)选择性必修第三册 7.4 二项分布与超几何分布
一、单选题
1.某小组有名男生、名女生,从中任选名同学参加活动,若表示选出女生的人数,则( )
A. B. C. D.
2.已知随机变量服从二项分布,若,,则( )
A. B. C. D.
3.某电子管的正品率为,次品率为,现对该批电子管进行测试,那么在三次测试中恰有一次测到正品的概率是( )
A. B. C. D.
4.抛掷一枚质地均匀的正方体骰子4次,设表示向上一面出现6点的次数,则的数学期望的值为( )
A. B. C. D.
5.某产品正品率为,次品率为,现对该产品进行测试,设第ξ次首次测到正品,则P(ξ=3)=( )
A. B. C. D.
6.某同学进行3分投篮训练,若该同学投中的概率为,他连续投篮n次至少得到3分的概率大于0.9,那么n的最小值是( )
A.3 B.4 C.5 D.6
7.已知随机变量满足,且,若,则( )
A.0.5 B.0.8 C.0.2 D.0.4
8.若随机变量,,若,则( )
A. B. C. D.
9.下列事件:①运动员甲射击一次,“射中9环”与“射中8环”;②甲 乙两名运动员各射击一次,“甲射中10环”与“乙射中9环”;③甲 乙两名运动员各射击一次,“甲 乙都射中目标”与“甲 乙都没射中目标”;④在相同的条件下,甲射击10次5次击中目标.其中是独立重复试验的是( )
A.① B.② C.③ D.④
10.一个袋子里装有大小相同的3个红球和2个黄球,从中同时取出2个球,其中红球个数的数学期望是( )
A. B. C. D.
11.掷一枚质地均匀的骰子n次,设出现k次点数为1的概率为,若,则当取最大值时,k为( )
A.3 B.4 C.8 D.10
12.设随机变量,,若,则( )
A. B. C. D.
13.设随机变量,函数没有零点的概率是0.5,则( )
附:若,则,.
A.0.1587 B.0.1359 C.0.2718 D.0.3413
14.已知某种药物对某种疾病的治愈率为,现有位患有该病的患者服用了这种药物,位患者是否会被治愈是相互独立的,则恰有位患者被治愈的概率为( )
A. B. C. D.
15.为了防止受到核污染的产品影响我国民众的身体健康,有关部门要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为,第二轮检测不合格的概率为,两轮检测是否合格相互没有影响,若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则( )
A. B. C. D.
二、填空题
16.某电视台开展有奖答题活动,每次要求答30个选择题,每个选择题有4个选项,其中有且只有一个正确答案,每一题选对得5分,选错或不选得0分,满分150分.规定满100分拿三等奖,满120分拿二等奖,满140分拿一等奖.有一个选手选对任一题的概率都是0.8,则该选手可能拿到________等奖.
17.一台仪器每启动一次都随机地出现一个4位的二进制数,其中的各位数字中,,出现0的概率为,出现1的概率为.若启动一次出现的数字为,则称这次试验成功.若成功一次得2分,失败一次得分,则54次这样的重复试验的总得分的方差为______.
18.为了防止受到核污染的产品影响我国民众的身体健康,要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为,第二轮检测不合格的概率为,两轮检测是否合格相互没有影响.若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则P(X≥-80)=________.
三、解答题
19.甲、乙两位同学进行篮球三分球投篮比赛,甲每次投中的概率为,乙每次投中的概率为,每人分别进行三次投篮.
(1)记甲投中的次数为,求的分布列;
(2)求乙至多投中2次的概率.
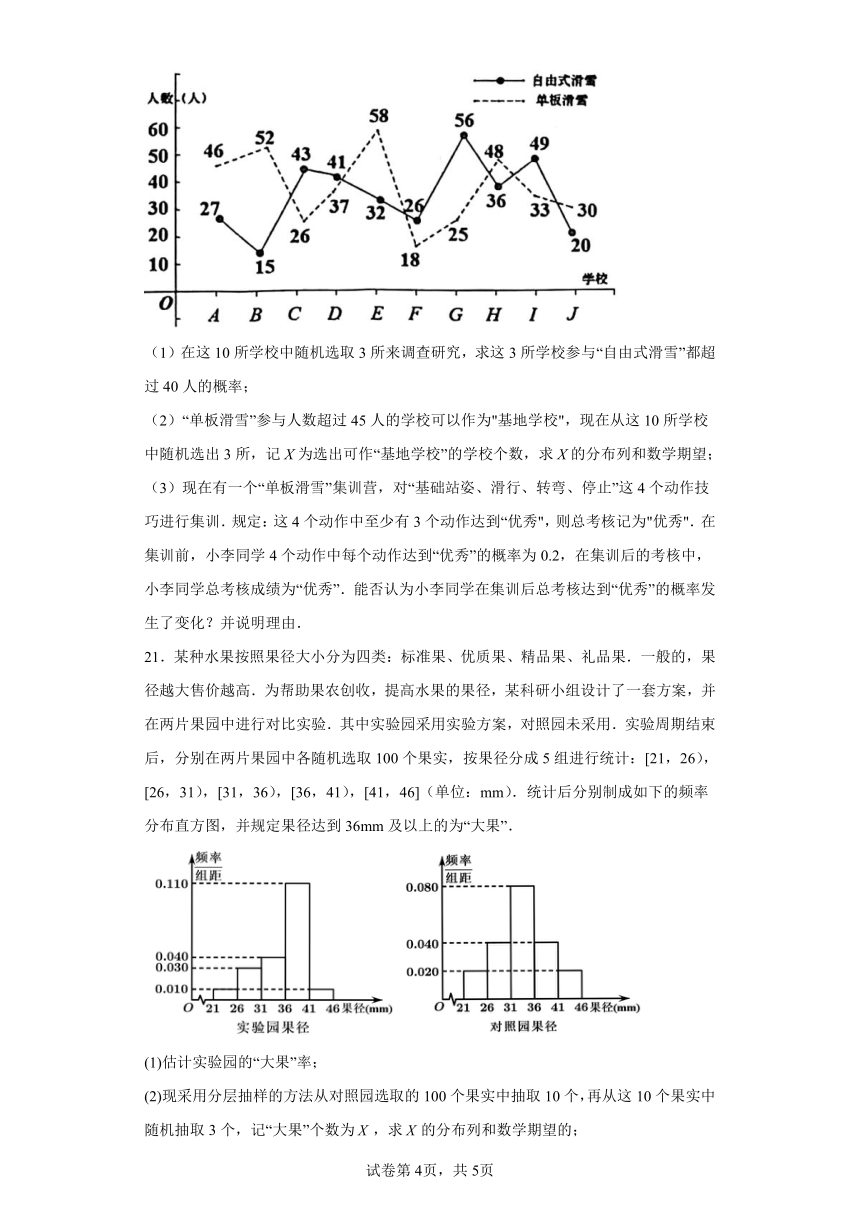
20.2022年冬季奥林匹克运动会主办城市是北京,北京成为第一个举办过夏季奥林匹克运动会和冬季奥林匹克运动会以及亚洲运动会三项国际赛事的城市!为迎接冬奥会的到来,某地很多中小学开展了模拟冬奥会赛事的活动,为了深入了解学生在“自由式滑雪”和“单板滑雪”两项活动的参与情况,在该地随机选取了10所学校进行研究,得到如下数据:
(1)在这10所学校中随机选取3所来调查研究,求这3所学校参与“自由式滑雪”都超过40人的概率;
(2)“单板滑雪”参与人数超过45人的学校可以作为"基地学校",现在从这10所学校中随机选出3所,记X为选出可作“基地学校”的学校个数,求X的分布列和数学期望;
(3)现在有一个“单板滑雪”集训营,对“基础站姿、滑行、转弯、停止”这4个动作技巧进行集训.规定:这4个动作中至少有3个动作达到“优秀",则总考核记为"优秀".在集训前,小李同学4个动作中每个动作达到“优秀”的概率为0.2,在集训后的考核中,小李同学总考核成绩为“优秀”.能否认为小李同学在集训后总考核达到“优秀”的概率发生了变化?并说明理由.
21.某种水果按照果径大小分为四类:标准果、优质果、精品果、礼品果.一般的,果径越大售价越高.为帮助果农创收,提高水果的果径,某科研小组设计了一套方案,并在两片果园中进行对比实验.其中实验园采用实验方案,对照园未采用.实验周期结束后,分别在两片果园中各随机选取100个果实,按果径分成5组进行统计:[21,26),[26,31),[31,36),[36,41),[41,46](单位:mm).统计后分别制成如下的频率分布直方图,并规定果径达到36mm及以上的为“大果”.
(1)估计实验园的“大果”率;
(2)现采用分层抽样的方法从对照园选取的100个果实中抽取10个,再从这10个果实中随机抽取3个,记“大果”个数为,求的分布列和数学期望的;
(3)以频率估计概率,从对照园这批果实中随机抽取个,设其中恰有2个“大果”的概率为,当最大时,写出的值(只需写出结论).
22.溺水 校园欺凌等与学生安全有关的问题越来越受到社会的关注和重视,为了普及安全教育,某市组织了一次学生安全知识竞赛,规定每队3人,每人回答一个问题,答对得1分,答错得0分.在竞赛中,甲 乙两个中学代表队相遇,假设甲队3人回答正确的概率均为,乙队3人回答正确的概率分别为,,,且两队各人回答问题正确与否互不影响.
(1)求甲队总得分为2分且乙队总得分为1分的概率;
(2)求甲队总得分X的分布列和数学期望.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
本题首先可以求出当时的概率,然后求出当时的概率,最后两者相加,即可得出结果.
【详解】
当时,;
当时,,
则,
故选:C.
本题考查超几何分布的概率计算公式,能否将分为、两种情况是解决本题的关键,考查计算能力,是简单题.
2.A
由二项分布的均值和方差公式列方程组求解.
【详解】
由题意,解得.
故选:A.
3.C
恰有一次测到正品,则有两次测到次品,再根据独立重复实验求概率得方法即可得解.
【详解】
解:由题意可知,三次测试中恰有一次测到正品,则有两次测到次品,故所求事件的概率为.
故选:C.
4.D
先确定抛掷一枚质地均匀的正方体骰子1次,向上一面出现6点的概率,再根据二项分布数学期望公式求得结果.
【详解】
抛掷一枚质地均匀的正方体骰子1次,向上一面出现6点的概率为
故选:D
本题考查二项分布数学期望公式,考查基本分析求解能力,属基础题.
5.C
由已知得“ξ=3”表示第一次和第二次都测到了次品,第三次测到正品,由此能求出结果.
【详解】
解:因为某产品正品率为,次品率为,现对该产品进行测试,设第ξ次首次测到正品,
所以“ξ=3”表示第一次和第二次都测到了次品,第三次测到正品,
所以P(ξ=3) = ,
故选:C
此题考查概率的求法,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用,属于基础题.
6.B
先计算一次都不中的概率,再求至少中一次的概率,列关系求解即可.
【详解】
由题意可知,该同学连投n次,一次都不中的概率为:,
故n次投篮至少得到3分即至少中一次的概率为,得,∴.
故选:B.
本题考查了n次独立重复实验至少有一次发生的概率和指数不等式,属于基础题.
7.D
由二项分布的性质推导出,解得,从而,再由,能求出.
【详解】
解:随机变量,满足,且,,
,解得,
,
,
.
故选:.
本题考查离散型随机变量的方差的求法,考查二项分布及方差的性质等基础知识,考查运算求解能力,属于基础题.
8.A
根据二项分布列式,计算出,然后利用正态分布的特点计算的值.
【详解】
由题意,,解得,则,所以.
故选:A.
9.D
根据互斥事件、相互独立事件,以及独立重复试验的定义可以判断:①,甲射击一次,“射中9环”与“射中8环”是一个实验的两个结果,是互斥事件;②是相互独立事件;③是互斥事件;④是独立重复试验.
【详解】
①和③符合互斥事件的概念,是互斥事件;
②是相互独立事件;
④是独立重复试验;
所以只有④符合题意,
故选:D.
10.C
记同时取出的2个球中红球的个数为X,则,再根据超几何分布的期望公式计算可得;
【详解】
解:记同时取出的2个球中红球的个数为X,则X服从参数为,,的超几何分布,所以.
故选:C
11.A
由题意可知出现的点数,根据二项分布求解即可.
【详解】
掷一枚质地均匀的骰子20次,其中出现点数为1的次数为X,
则,
当时,,;
当时,,.
因此当时,取最大值.
故选:A
12.A
先建立方程求出,再计算即可.
【详解】
解:因为随机变量,,
所以,则,
因为,即,解得
随机变量中,
,
故选:A
本题考查二项分布概率公式,是基础题.
13.B
首先根据函数没有零点求出的取值范围,再根据没有零点的概率是,得到,再根据正态曲线的性质得到的值;然后再根据正态曲线的对称性求出的值即可.
【详解】
若函数没有零点,
∴二次方程无实根,
∴,∴.
又∵没有零点的概率是0.5,
∴.
由正态曲线的对称性知,
∴,∴,,
∴,,,,
∴,,
∴
.
故选:B.
14.B
利用二项分布概率计算公式即可解得
【详解】
由已知位患者被治愈是相互独立的,每位患者被治愈的概率为,则不被治愈的概率为
所以位患者中恰有1为患者被治愈的概率为
故选:B
结论点睛:二项分布概率公式,n是试验次数,k是指定事件发生的次数,p是指定事件在一次试验中发生的概率,考查学生的逻辑能力与运算能力,属于基础题.
15.B
先求得该产品能销售的概率,易知X的所有可能取值为﹣320,﹣200,﹣80,40,160,然后利用二项分布求解.
【详解】
由题意得该产品能销售的概率为,
易知X的所有可能取值为﹣320,﹣200,﹣80,40,160,
设表示一箱产品中可以销售的件数,则,
所以,
所以,,
,
故,
,
故选:B.
16.二
根据题意得到选手选对题的个数服从二项分别,求得期望,得到选手的得分,即可求解.
【详解】
由题意,选手选对任一题的概率都是0.8,
所以选手选对题的个数服从二项分布,即,
所以,可得(分),所以可能拿到二等奖.
故答案为:二
17.
由题可求出试验成功的概率,再利用二项分布及其方差的性质即求.
【详解】
启动一次出现数字为的概率,
设试验成功的次数为,则,
所以的方差为,
易得总得分,所以.
故答案为:.
18.
首先求某产品两轮检测合格的概率,X的所有可能取值为-320,-200,-80,40,160,然后根据二项分布求其概率,并计算.
【详解】
由题意得该产品能销售的概率为,易知X的所有可能取值为-320,-200,-80,40,160,设ξ表示一箱产品中可以销售的件数,则ξ~B,
所以,
所以P(X=-80)=P(ξ=2)= ,
P(X=40)=P(ξ=3)=,
P(X=160)=P(ξ=4)=,
故P(X≥-80)=P(X=-80)+P(X=40)+P(X=160)=.
本题考查独立事件同时发生的概率和二项分布,意在考查分析问题和解决问题的能力,对于此类考题,要注意认真审题,从数学与实际生活两个角度来理解问题的实质,将问题成功转化为古典概型,独立事件、互斥事件等概率模型求解,因此对概率型应用性问题,理解是基础,转化是关键.
19.(1)答案见解析;(2).
(1)可得的可能取值为0,1,2,3,求出取不同值时的概率即可得出分布列;
(2)求出对立事件乙3次全部投中的概率即可求解.
【详解】
(1)的可能取值为0,1,2,3.
,
,
,
,
的分布列为
0 1 2 3
(2)乙至多投中2次的对立事件为乙3次全部投中,
则乙至多投中2次的概率为.
20.(1);(2)分布列见解析,;(3)无法确定总考核达到“优”的概率发生了变化,理由见解析.
(1)利用古典概型结合组合公式即可求得结果;(2)写出X的可能值,利用超几何分布求得分布列,利用数学期望公式求得期望;(3)利用二项分布分别求得集训前,小李同学总考核为“优”的概率,经比较得出结论.
【详解】
解:(1)记“从10所学校中选出的3所学校参与“自由式滑雪”都超过40人”的事件为A;
参与“自由式滑雪”的人数超过40人的学校共4所,随机选择3所学校共种,
所以.
(2)X的所有可能取值为0,1,2,3,参加“单板滑雪”人数在45人以上的学校共4所.
所以,,,.
所以X的分布列为
X 0 1 2 3
P
所以.
(3)答案不唯一.
答案示例1:可以认为小李同学在集训后总考核为“优”的概率发生了变化.理由如下:
集训前,小李同学总考核为“优”的概率为:.
集训前,小李同学总考核为“优”的概率非常小,一且发生,就有理由认为集训后总考核达到“优”的概率发生了变化.
答案示例2:无法确定,理由如下:
集训前,小李同学总考核为“优”的概率为:.
虽然概率非常小,但是也可能发生,所以,无法确定总考核达到“优”的概率发生了变化.
21.(1);
(2)分布列见解析,;
(3)6.
(1)根据频率直方图计算果径达到36mm及以上组的频率和,即为所求的“大果”率
(2)由分层抽样可得:抽取10个大果有3个,则“大果”个数可能取值为,并求对应概率,写出分布列,进而求期望.
(3)由,应用不等式法求最大时的值.
(1)
由实验园的频率分布直方图得:,
所以估计实验园的“大果”率为
(2)
由对照园的频率分布直方图得:这个果实中大果的个数为个.
采用分层抽样的方法从100个果实中抽取10个,其中大果有个,
从这10个果实中随机抽取3个,记“大果”个数为,则的可能取值为,
,,,,
所以的分布列为:
0 1 2 3
所以.
(3)
由题设知:,而,,
∴要使最大,则且,
∴,故.
22.(1);
(2)分布列见解析,.
(1)利用独立事件的乘法公式及互斥事件加法公式求甲队总得分为2分且乙队总得分为1分的概率;
(2)由题意有,利用二项分布概率公式求各可能值对应的概率,进而写出分布列,再根据分布列求期望即可.
(1)
由题设,甲队得2分,即2人答对1人答错,概率为,
乙队得1分,即1人答对2人答错,概率为,
所以甲队总得分为2分且乙队总得分为1分的概率.
(2)
由题设,,且,,,,
甲队总得分X的分布列如下:
0 1 2 3
所以.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.某小组有名男生、名女生,从中任选名同学参加活动,若表示选出女生的人数,则( )
A. B. C. D.
2.已知随机变量服从二项分布,若,,则( )
A. B. C. D.
3.某电子管的正品率为,次品率为,现对该批电子管进行测试,那么在三次测试中恰有一次测到正品的概率是( )
A. B. C. D.
4.抛掷一枚质地均匀的正方体骰子4次,设表示向上一面出现6点的次数,则的数学期望的值为( )
A. B. C. D.
5.某产品正品率为,次品率为,现对该产品进行测试,设第ξ次首次测到正品,则P(ξ=3)=( )
A. B. C. D.
6.某同学进行3分投篮训练,若该同学投中的概率为,他连续投篮n次至少得到3分的概率大于0.9,那么n的最小值是( )
A.3 B.4 C.5 D.6
7.已知随机变量满足,且,若,则( )
A.0.5 B.0.8 C.0.2 D.0.4
8.若随机变量,,若,则( )
A. B. C. D.
9.下列事件:①运动员甲射击一次,“射中9环”与“射中8环”;②甲 乙两名运动员各射击一次,“甲射中10环”与“乙射中9环”;③甲 乙两名运动员各射击一次,“甲 乙都射中目标”与“甲 乙都没射中目标”;④在相同的条件下,甲射击10次5次击中目标.其中是独立重复试验的是( )
A.① B.② C.③ D.④
10.一个袋子里装有大小相同的3个红球和2个黄球,从中同时取出2个球,其中红球个数的数学期望是( )
A. B. C. D.
11.掷一枚质地均匀的骰子n次,设出现k次点数为1的概率为,若,则当取最大值时,k为( )
A.3 B.4 C.8 D.10
12.设随机变量,,若,则( )
A. B. C. D.
13.设随机变量,函数没有零点的概率是0.5,则( )
附:若,则,.
A.0.1587 B.0.1359 C.0.2718 D.0.3413
14.已知某种药物对某种疾病的治愈率为,现有位患有该病的患者服用了这种药物,位患者是否会被治愈是相互独立的,则恰有位患者被治愈的概率为( )
A. B. C. D.
15.为了防止受到核污染的产品影响我国民众的身体健康,有关部门要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为,第二轮检测不合格的概率为,两轮检测是否合格相互没有影响,若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则( )
A. B. C. D.
二、填空题
16.某电视台开展有奖答题活动,每次要求答30个选择题,每个选择题有4个选项,其中有且只有一个正确答案,每一题选对得5分,选错或不选得0分,满分150分.规定满100分拿三等奖,满120分拿二等奖,满140分拿一等奖.有一个选手选对任一题的概率都是0.8,则该选手可能拿到________等奖.
17.一台仪器每启动一次都随机地出现一个4位的二进制数,其中的各位数字中,,出现0的概率为,出现1的概率为.若启动一次出现的数字为,则称这次试验成功.若成功一次得2分,失败一次得分,则54次这样的重复试验的总得分的方差为______.
18.为了防止受到核污染的产品影响我国民众的身体健康,要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为,第二轮检测不合格的概率为,两轮检测是否合格相互没有影响.若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则P(X≥-80)=________.
三、解答题
19.甲、乙两位同学进行篮球三分球投篮比赛,甲每次投中的概率为,乙每次投中的概率为,每人分别进行三次投篮.
(1)记甲投中的次数为,求的分布列;
(2)求乙至多投中2次的概率.
20.2022年冬季奥林匹克运动会主办城市是北京,北京成为第一个举办过夏季奥林匹克运动会和冬季奥林匹克运动会以及亚洲运动会三项国际赛事的城市!为迎接冬奥会的到来,某地很多中小学开展了模拟冬奥会赛事的活动,为了深入了解学生在“自由式滑雪”和“单板滑雪”两项活动的参与情况,在该地随机选取了10所学校进行研究,得到如下数据:
(1)在这10所学校中随机选取3所来调查研究,求这3所学校参与“自由式滑雪”都超过40人的概率;
(2)“单板滑雪”参与人数超过45人的学校可以作为"基地学校",现在从这10所学校中随机选出3所,记X为选出可作“基地学校”的学校个数,求X的分布列和数学期望;
(3)现在有一个“单板滑雪”集训营,对“基础站姿、滑行、转弯、停止”这4个动作技巧进行集训.规定:这4个动作中至少有3个动作达到“优秀",则总考核记为"优秀".在集训前,小李同学4个动作中每个动作达到“优秀”的概率为0.2,在集训后的考核中,小李同学总考核成绩为“优秀”.能否认为小李同学在集训后总考核达到“优秀”的概率发生了变化?并说明理由.
21.某种水果按照果径大小分为四类:标准果、优质果、精品果、礼品果.一般的,果径越大售价越高.为帮助果农创收,提高水果的果径,某科研小组设计了一套方案,并在两片果园中进行对比实验.其中实验园采用实验方案,对照园未采用.实验周期结束后,分别在两片果园中各随机选取100个果实,按果径分成5组进行统计:[21,26),[26,31),[31,36),[36,41),[41,46](单位:mm).统计后分别制成如下的频率分布直方图,并规定果径达到36mm及以上的为“大果”.
(1)估计实验园的“大果”率;
(2)现采用分层抽样的方法从对照园选取的100个果实中抽取10个,再从这10个果实中随机抽取3个,记“大果”个数为,求的分布列和数学期望的;
(3)以频率估计概率,从对照园这批果实中随机抽取个,设其中恰有2个“大果”的概率为,当最大时,写出的值(只需写出结论).
22.溺水 校园欺凌等与学生安全有关的问题越来越受到社会的关注和重视,为了普及安全教育,某市组织了一次学生安全知识竞赛,规定每队3人,每人回答一个问题,答对得1分,答错得0分.在竞赛中,甲 乙两个中学代表队相遇,假设甲队3人回答正确的概率均为,乙队3人回答正确的概率分别为,,,且两队各人回答问题正确与否互不影响.
(1)求甲队总得分为2分且乙队总得分为1分的概率;
(2)求甲队总得分X的分布列和数学期望.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
本题首先可以求出当时的概率,然后求出当时的概率,最后两者相加,即可得出结果.
【详解】
当时,;
当时,,
则,
故选:C.
本题考查超几何分布的概率计算公式,能否将分为、两种情况是解决本题的关键,考查计算能力,是简单题.
2.A
由二项分布的均值和方差公式列方程组求解.
【详解】
由题意,解得.
故选:A.
3.C
恰有一次测到正品,则有两次测到次品,再根据独立重复实验求概率得方法即可得解.
【详解】
解:由题意可知,三次测试中恰有一次测到正品,则有两次测到次品,故所求事件的概率为.
故选:C.
4.D
先确定抛掷一枚质地均匀的正方体骰子1次,向上一面出现6点的概率,再根据二项分布数学期望公式求得结果.
【详解】
抛掷一枚质地均匀的正方体骰子1次,向上一面出现6点的概率为
故选:D
本题考查二项分布数学期望公式,考查基本分析求解能力,属基础题.
5.C
由已知得“ξ=3”表示第一次和第二次都测到了次品,第三次测到正品,由此能求出结果.
【详解】
解:因为某产品正品率为,次品率为,现对该产品进行测试,设第ξ次首次测到正品,
所以“ξ=3”表示第一次和第二次都测到了次品,第三次测到正品,
所以P(ξ=3) = ,
故选:C
此题考查概率的求法,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用,属于基础题.
6.B
先计算一次都不中的概率,再求至少中一次的概率,列关系求解即可.
【详解】
由题意可知,该同学连投n次,一次都不中的概率为:,
故n次投篮至少得到3分即至少中一次的概率为,得,∴.
故选:B.
本题考查了n次独立重复实验至少有一次发生的概率和指数不等式,属于基础题.
7.D
由二项分布的性质推导出,解得,从而,再由,能求出.
【详解】
解:随机变量,满足,且,,
,解得,
,
,
.
故选:.
本题考查离散型随机变量的方差的求法,考查二项分布及方差的性质等基础知识,考查运算求解能力,属于基础题.
8.A
根据二项分布列式,计算出,然后利用正态分布的特点计算的值.
【详解】
由题意,,解得,则,所以.
故选:A.
9.D
根据互斥事件、相互独立事件,以及独立重复试验的定义可以判断:①,甲射击一次,“射中9环”与“射中8环”是一个实验的两个结果,是互斥事件;②是相互独立事件;③是互斥事件;④是独立重复试验.
【详解】
①和③符合互斥事件的概念,是互斥事件;
②是相互独立事件;
④是独立重复试验;
所以只有④符合题意,
故选:D.
10.C
记同时取出的2个球中红球的个数为X,则,再根据超几何分布的期望公式计算可得;
【详解】
解:记同时取出的2个球中红球的个数为X,则X服从参数为,,的超几何分布,所以.
故选:C
11.A
由题意可知出现的点数,根据二项分布求解即可.
【详解】
掷一枚质地均匀的骰子20次,其中出现点数为1的次数为X,
则,
当时,,;
当时,,.
因此当时,取最大值.
故选:A
12.A
先建立方程求出,再计算即可.
【详解】
解:因为随机变量,,
所以,则,
因为,即,解得
随机变量中,
,
故选:A
本题考查二项分布概率公式,是基础题.
13.B
首先根据函数没有零点求出的取值范围,再根据没有零点的概率是,得到,再根据正态曲线的性质得到的值;然后再根据正态曲线的对称性求出的值即可.
【详解】
若函数没有零点,
∴二次方程无实根,
∴,∴.
又∵没有零点的概率是0.5,
∴.
由正态曲线的对称性知,
∴,∴,,
∴,,,,
∴,,
∴
.
故选:B.
14.B
利用二项分布概率计算公式即可解得
【详解】
由已知位患者被治愈是相互独立的,每位患者被治愈的概率为,则不被治愈的概率为
所以位患者中恰有1为患者被治愈的概率为
故选:B
结论点睛:二项分布概率公式,n是试验次数,k是指定事件发生的次数,p是指定事件在一次试验中发生的概率,考查学生的逻辑能力与运算能力,属于基础题.
15.B
先求得该产品能销售的概率,易知X的所有可能取值为﹣320,﹣200,﹣80,40,160,然后利用二项分布求解.
【详解】
由题意得该产品能销售的概率为,
易知X的所有可能取值为﹣320,﹣200,﹣80,40,160,
设表示一箱产品中可以销售的件数,则,
所以,
所以,,
,
故,
,
故选:B.
16.二
根据题意得到选手选对题的个数服从二项分别,求得期望,得到选手的得分,即可求解.
【详解】
由题意,选手选对任一题的概率都是0.8,
所以选手选对题的个数服从二项分布,即,
所以,可得(分),所以可能拿到二等奖.
故答案为:二
17.
由题可求出试验成功的概率,再利用二项分布及其方差的性质即求.
【详解】
启动一次出现数字为的概率,
设试验成功的次数为,则,
所以的方差为,
易得总得分,所以.
故答案为:.
18.
首先求某产品两轮检测合格的概率,X的所有可能取值为-320,-200,-80,40,160,然后根据二项分布求其概率,并计算.
【详解】
由题意得该产品能销售的概率为,易知X的所有可能取值为-320,-200,-80,40,160,设ξ表示一箱产品中可以销售的件数,则ξ~B,
所以,
所以P(X=-80)=P(ξ=2)= ,
P(X=40)=P(ξ=3)=,
P(X=160)=P(ξ=4)=,
故P(X≥-80)=P(X=-80)+P(X=40)+P(X=160)=.
本题考查独立事件同时发生的概率和二项分布,意在考查分析问题和解决问题的能力,对于此类考题,要注意认真审题,从数学与实际生活两个角度来理解问题的实质,将问题成功转化为古典概型,独立事件、互斥事件等概率模型求解,因此对概率型应用性问题,理解是基础,转化是关键.
19.(1)答案见解析;(2).
(1)可得的可能取值为0,1,2,3,求出取不同值时的概率即可得出分布列;
(2)求出对立事件乙3次全部投中的概率即可求解.
【详解】
(1)的可能取值为0,1,2,3.
,
,
,
,
的分布列为
0 1 2 3
(2)乙至多投中2次的对立事件为乙3次全部投中,
则乙至多投中2次的概率为.
20.(1);(2)分布列见解析,;(3)无法确定总考核达到“优”的概率发生了变化,理由见解析.
(1)利用古典概型结合组合公式即可求得结果;(2)写出X的可能值,利用超几何分布求得分布列,利用数学期望公式求得期望;(3)利用二项分布分别求得集训前,小李同学总考核为“优”的概率,经比较得出结论.
【详解】
解:(1)记“从10所学校中选出的3所学校参与“自由式滑雪”都超过40人”的事件为A;
参与“自由式滑雪”的人数超过40人的学校共4所,随机选择3所学校共种,
所以.
(2)X的所有可能取值为0,1,2,3,参加“单板滑雪”人数在45人以上的学校共4所.
所以,,,.
所以X的分布列为
X 0 1 2 3
P
所以.
(3)答案不唯一.
答案示例1:可以认为小李同学在集训后总考核为“优”的概率发生了变化.理由如下:
集训前,小李同学总考核为“优”的概率为:.
集训前,小李同学总考核为“优”的概率非常小,一且发生,就有理由认为集训后总考核达到“优”的概率发生了变化.
答案示例2:无法确定,理由如下:
集训前,小李同学总考核为“优”的概率为:.
虽然概率非常小,但是也可能发生,所以,无法确定总考核达到“优”的概率发生了变化.
21.(1);
(2)分布列见解析,;
(3)6.
(1)根据频率直方图计算果径达到36mm及以上组的频率和,即为所求的“大果”率
(2)由分层抽样可得:抽取10个大果有3个,则“大果”个数可能取值为,并求对应概率,写出分布列,进而求期望.
(3)由,应用不等式法求最大时的值.
(1)
由实验园的频率分布直方图得:,
所以估计实验园的“大果”率为
(2)
由对照园的频率分布直方图得:这个果实中大果的个数为个.
采用分层抽样的方法从100个果实中抽取10个,其中大果有个,
从这10个果实中随机抽取3个,记“大果”个数为,则的可能取值为,
,,,,
所以的分布列为:
0 1 2 3
所以.
(3)
由题设知:,而,,
∴要使最大,则且,
∴,故.
22.(1);
(2)分布列见解析,.
(1)利用独立事件的乘法公式及互斥事件加法公式求甲队总得分为2分且乙队总得分为1分的概率;
(2)由题意有,利用二项分布概率公式求各可能值对应的概率,进而写出分布列,再根据分布列求期望即可.
(1)
由题设,甲队得2分,即2人答对1人答错,概率为,
乙队得1分,即1人答对2人答错,概率为,
所以甲队总得分为2分且乙队总得分为1分的概率.
(2)
由题设,,且,,,,
甲队总得分X的分布列如下:
0 1 2 3
所以.
答案第1页,共2页
答案第1页,共2页
