2.3直线的交点坐标与距离公式 同步练习(Word版含解析)
文档属性
| 名称 | 2.3直线的交点坐标与距离公式 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 644.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 00:00:00 | ||
图片预览




文档简介
人教A版(2019)选择性必修第一册 2.3 直线的交点坐标与距离公式
一、单选题
1.已知直线与直线和的距离相等,则的方程是( )
A. B.
C. D.
2.已知三条直线、和中没有任何两条平行,但它们不能构成三角形的三边,则实数的值为( )
A. B. C. D.
3.点(2,1)到直线l:x-2y+2=0的距离为( )
A. B.
C. D.0
4.唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河”,诗中隐含着一个有趣的数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在的位置为,若将军从山脚下的点处出发,河岸线所在直线l的方程为,则“将军饮马”的最短总路程是( )
A. B. C. D.
5.两条平行直线3x+4y-10=0与ax+8y+11=0之间的距离为( )
A. B. C. D.
6.若(-1,-2)为直线2x+3y+a=0与直线bx-y-1=0的交点,则ab的值为( )
A.8 B.-8
C.9 D.-9
7.已知平面上两点,,,则的最小值为( )
A.3 B. C.2 D.
8.直线上与点的距离等于的点的坐标是( )
A. B.
C.或 D.或
9.已知点P,Q分别在直线与直线上,且,点,,则的最小值为.
A. B. C. D.
10.直线y=4x﹣5关于点P(2,1)对称的直线方程是( )
A.y=4x+5 B.y=4x﹣5 C.y=4x﹣9 D.y=4x+9
11.点到直线的距离为( )
A. B. C. D.
12.已知M,N分别是曲线上的两个动点,P为直线上的一个动点,则的最小值为
A. B. C.2 D.3
二、填空题
13.直线与直线之间的距离为__________.
14.在同一平面内,已知直线和直线,若直线l到直线的距离与到直线的距离之比为,则直线l的方程为______.
15.已知中,,,点C在直线上,若的面积为10,则点C的坐标为______.
16.若某直线被两平行线与所截得的线段的长为,则该直线的倾斜角大小为_______.
三、解答题
17.已知三条直线:,直线:和:,且与之间的距离是.
(1)求的值;
(2)求经过直线与的交点,且与点的距离为3的直线的方程.
18.求点到直线的距离.
19.已知直线.
(1)若直线的倾斜角为,求实数a的值;
(2)若直线在x轴上的截距为,求实数a的值;
(3)若直线与直线平行,求两平行直线与之间的距离.
20.已知三角形的顶点为,,.
(1)求直线的方程;
(2)从①、②这两个问题中选择一个作答.
①求点关于直线的对称点的坐标.
②若直线过点且与直线交于点,,求直线的方程.
21.一河流同侧有两个村庄A,B,两村庄计划在河上共建一水电站供两村使用,已知A,B两村到河边的垂直距离分别为300 m和700 m,且两村相距500 m,问:水电站建于何处送电到两村的电线用料最省?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
设所求直线方程为:,根据该直线与和的距离相等,建立方程求解可得选项.
【详解】
设所求直线l方程为:,
因为直线l与;距离相等,所以,解得,
所以所求直线方程为:,
故选:D.
2.A
由三条直线过同一点,求得,并判断不重合即得.
【详解】
由已知得三条直线必过同一个点,则联立,解得这两条直线的交点为,
代入可得,此时没有两条直线重合.
故选:A.
3.B
直接运用点到直线距离公式进行求解即可.
【详解】
点(2,1)到直线l:x-2y+2=0的距离为,
故选:B
4.D
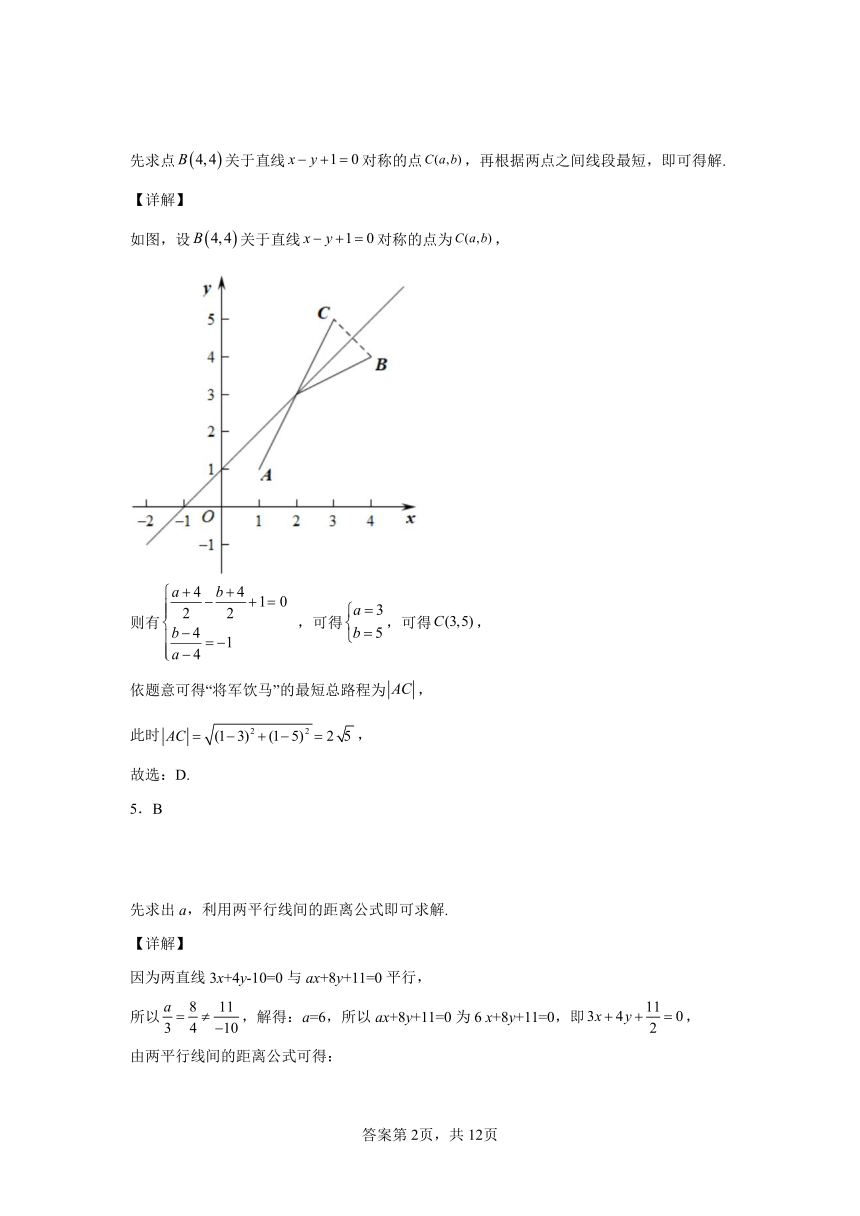
先求点关于直线对称的点,再根据两点之间线段最短,即可得解.
【详解】
如图,设关于直线对称的点为,
则有 ,可得,可得,
依题意可得“将军饮马”的最短总路程为,
此时,
故选:D.
5.B
先求出a,利用两平行线间的距离公式即可求解.
【详解】
因为两直线3x+4y-10=0与ax+8y+11=0平行,
所以,解得:a=6,所以ax+8y+11=0为6 x+8y+11=0,即,
由两平行线间的距离公式可得:
两条平行直线3x+4y-10=0与6x+8y+11=0之间的距离为:.
故选:B.
6.A
由x=-1,y=-2是方程2x+3y+a=0与方程bx-y-1=0的公共解求解.
【详解】
由题意得,
解得,
所以ab=8.
故选:A
7.D
利用两点间距离公式,结合配方法进行求解即可.
【详解】
根据题意,平面上两点,,,
则,则有,
则的最小值为,
故选:D.
8.C
设所求点坐标为,根据已知条件列方程,由此求得正确答案.
【详解】
设所求点的坐标为,有,且,
两式联立解得或.
故选:C
9.B
设,则四边形为平行四边形,故而就是的最小值,又的最小值就是.
【详解】
因为,故,
,故,所以,
又,所以,故四边形为平行四边形,
,
因为,当且仅当三点共线时等号成立,
的最小值为,选B.
本题考查坐标平面中线段和的最值,注意利用几何性质把问题转化为一个动点(在直线上)与两个定点之间的连线段的和的最值,这类问题属于中档题.
10.C
设直线上的点关于点的对称点的坐标为,求出,,再代入直线中即可得到对称直线的方程.
【详解】
设直线上的点关于点的对称点的坐标为,
所以,,所以,,
将其代入直线中,得到,化简得,
故选:C.
本题主要考查的知识要点:直线的方程和中点坐标公式,属于基础题.
11.B
直接代入点到直线距离公式,即可得解.
【详解】
根据距离公式可得:
点到直线的距离,
故选:B.
12.D
求出圆心关于的对称点为,则的最小值是.
【详解】
解:圆的圆心,半径为 ,圆,圆心,半径为,
圆心关于的对称点为,
解得故
.
故选.
本题考查圆的方程,考查点线对称,考查学生分析解决问题的能力,属于基础题.
13.
化简直线为,结合两平行线间的距离公式,即可求解.
【详解】
化简直线为,
根据平行线间的距离公式,可得,
即直线与直线之间的距离为.
故答案为:.
14.或
由直线平行可设,根据距离之比即可得关于的方程,从而可求出直线l的方程.
【详解】
解:由题意知,直线的方程可转化为.易知,
所以可设直线l的方程为(且).
由题意,可得,解得或.
故直线l的方程为或,
即或.
故答案为: 或.
本题考查了直线间的距离公式,属于基础题.设出适合的直线方程是解本题的关键.
15.或
求出的距离,利用三角形的面积求出到直线的距离,求出的方程,结合点在直线上,利用点到直线的距离公式求出的坐标.
【详解】
设点到直线的距离为,
由题意知:,
,
直线的方程为,即,
点在直线上,
设,
,
或,
的坐标为或,故答案为或.
本题主要考查点到直线距离公式以及直线的两点式方程的应用,意在考查计算能力以及函数与方程思想的应用,属于中档题.
16.和
先由两平行直线的距离公式得直线与的距离为,再结合直线被两平行线所截得的线段的长为,求得该直线与直线所成角,然后结合直线的倾斜角为求解即可.
【详解】
解:由两平行直线的距离公式可得:
直线与的距离为,
又直线被两平行线与所截得的线段的长为,
即该直线与直线所成角,
又直线的倾斜角为,
则该直线的倾斜角大小为和,
故答案为:和.
本题考查了两平行直线的距离公式及直线的倾斜角,重点考查了运算能力,属基础题.
17.(1);(2)或.
(1)由与的距离是,代入两条平行直线间的距离公式,可得一个关于的方程,解方程即可求的值;
(2)求出交点坐标,设出直线方程,利用点到直线的距离公式求解即可.
【详解】
解:(1)即,
与的距离.
.
,.
(2)直线与的交点,由:,解得所以交点坐标.
当直线的斜率存在时,设所求的直线方程为:,即:.
点到直线的距离为3,
可得:,
解得,
所求直线方程.
当直线的斜率不存在时,,满足题意.
所求直线方程为:或.
本题考查直线方程的求法,直线的交点坐标,平行线之间的距离的求法,考查计算能力,属于中档题.
18.
直接利用距离公式计算可得;
【详解】
解:点到直线的距离
19.(1);(2);(3).
(1)根据直线,得到,再根据斜率与倾斜角的关系求解.
(2)根据直线,令得,再求解.
(3)根据直线与直线平行,则有求解,然后根据两平行直线间的距离公式求解.
【详解】
(1)因为直线,
所以,
又因为直线的倾斜角为,
所以,
解得.
(2)因为直线,
令得,,
解得.
(3)因为直线与直线平行,
所以,解得,
所以直线,
两平行直线与之间的距离 .
本题主要考查正弦得倾斜角,斜率,截距以及两直线的位置关系,还考查了运算求解的能力,属于中档题.
20.(1);(2)① ;②或.
(1)由,,即可求出直线的斜率,由点斜式即可写出直线的方程;
(2)选①由对称点的性质即可求出;
选②设出点的坐标,由两点间的距离公式列出方程,解出的值,根据、点的坐标即可求出直线的方程.
【详解】
解:(1)因为直线的斜率为,
所以直线的方程为:,
即直线的方程为:;
(2)问题①:
设的坐标为,则
解得:
点的坐标是;
问题②:
设的坐标为,
,
,
解得:或,
的坐标为或,
直线的方程为或.
方法点睛:求解直线方程时应该注意以下问题:
一是根据斜率求倾斜角,要注意倾斜角的范围;
二是求直线方程时,若不能断定直线是否具有斜率时,应对斜率存在与不存在加以讨论;
三是在用截距式时,应先判断截距是否为0,若不确定,则需分类讨论.
21.水电站建在P(90,0)处电线用料最省.
如图,以河流所在直线为x轴、y轴通过点A,建立平面直角坐标系,再求出点B的坐标,利用对称性求解.
【详解】
解:如图,以河流所在直线为x轴、y轴通过点A,建立平面直角坐标系,
则点A(0,300),B(x,700).
设点B在y轴上的射影为H,则x=|BH|==300,
故点B(300,700).
设点A关于x轴的对称点A′(0,-300),
则直线A′B的斜率k=,直线A′B的方程为y=x-300.
令y=0,得x=90,得点P(90,0),
故水电站建在P(90,0)处电线用料最省.
关键点睛:解答本题有两个关键,其一是:想到利用解析法来求解;其二是,能够利用数形结合利用对称性找到满足题意的位置.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知直线与直线和的距离相等,则的方程是( )
A. B.
C. D.
2.已知三条直线、和中没有任何两条平行,但它们不能构成三角形的三边,则实数的值为( )
A. B. C. D.
3.点(2,1)到直线l:x-2y+2=0的距离为( )
A. B.
C. D.0
4.唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河”,诗中隐含着一个有趣的数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在的位置为,若将军从山脚下的点处出发,河岸线所在直线l的方程为,则“将军饮马”的最短总路程是( )
A. B. C. D.
5.两条平行直线3x+4y-10=0与ax+8y+11=0之间的距离为( )
A. B. C. D.
6.若(-1,-2)为直线2x+3y+a=0与直线bx-y-1=0的交点,则ab的值为( )
A.8 B.-8
C.9 D.-9
7.已知平面上两点,,,则的最小值为( )
A.3 B. C.2 D.
8.直线上与点的距离等于的点的坐标是( )
A. B.
C.或 D.或
9.已知点P,Q分别在直线与直线上,且,点,,则的最小值为.
A. B. C. D.
10.直线y=4x﹣5关于点P(2,1)对称的直线方程是( )
A.y=4x+5 B.y=4x﹣5 C.y=4x﹣9 D.y=4x+9
11.点到直线的距离为( )
A. B. C. D.
12.已知M,N分别是曲线上的两个动点,P为直线上的一个动点,则的最小值为
A. B. C.2 D.3
二、填空题
13.直线与直线之间的距离为__________.
14.在同一平面内,已知直线和直线,若直线l到直线的距离与到直线的距离之比为,则直线l的方程为______.
15.已知中,,,点C在直线上,若的面积为10,则点C的坐标为______.
16.若某直线被两平行线与所截得的线段的长为,则该直线的倾斜角大小为_______.
三、解答题
17.已知三条直线:,直线:和:,且与之间的距离是.
(1)求的值;
(2)求经过直线与的交点,且与点的距离为3的直线的方程.
18.求点到直线的距离.
19.已知直线.
(1)若直线的倾斜角为,求实数a的值;
(2)若直线在x轴上的截距为,求实数a的值;
(3)若直线与直线平行,求两平行直线与之间的距离.
20.已知三角形的顶点为,,.
(1)求直线的方程;
(2)从①、②这两个问题中选择一个作答.
①求点关于直线的对称点的坐标.
②若直线过点且与直线交于点,,求直线的方程.
21.一河流同侧有两个村庄A,B,两村庄计划在河上共建一水电站供两村使用,已知A,B两村到河边的垂直距离分别为300 m和700 m,且两村相距500 m,问:水电站建于何处送电到两村的电线用料最省?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
设所求直线方程为:,根据该直线与和的距离相等,建立方程求解可得选项.
【详解】
设所求直线l方程为:,
因为直线l与;距离相等,所以,解得,
所以所求直线方程为:,
故选:D.
2.A
由三条直线过同一点,求得,并判断不重合即得.
【详解】
由已知得三条直线必过同一个点,则联立,解得这两条直线的交点为,
代入可得,此时没有两条直线重合.
故选:A.
3.B
直接运用点到直线距离公式进行求解即可.
【详解】
点(2,1)到直线l:x-2y+2=0的距离为,
故选:B
4.D
先求点关于直线对称的点,再根据两点之间线段最短,即可得解.
【详解】
如图,设关于直线对称的点为,
则有 ,可得,可得,
依题意可得“将军饮马”的最短总路程为,
此时,
故选:D.
5.B
先求出a,利用两平行线间的距离公式即可求解.
【详解】
因为两直线3x+4y-10=0与ax+8y+11=0平行,
所以,解得:a=6,所以ax+8y+11=0为6 x+8y+11=0,即,
由两平行线间的距离公式可得:
两条平行直线3x+4y-10=0与6x+8y+11=0之间的距离为:.
故选:B.
6.A
由x=-1,y=-2是方程2x+3y+a=0与方程bx-y-1=0的公共解求解.
【详解】
由题意得,
解得,
所以ab=8.
故选:A
7.D
利用两点间距离公式,结合配方法进行求解即可.
【详解】
根据题意,平面上两点,,,
则,则有,
则的最小值为,
故选:D.
8.C
设所求点坐标为,根据已知条件列方程,由此求得正确答案.
【详解】
设所求点的坐标为,有,且,
两式联立解得或.
故选:C
9.B
设,则四边形为平行四边形,故而就是的最小值,又的最小值就是.
【详解】
因为,故,
,故,所以,
又,所以,故四边形为平行四边形,
,
因为,当且仅当三点共线时等号成立,
的最小值为,选B.
本题考查坐标平面中线段和的最值,注意利用几何性质把问题转化为一个动点(在直线上)与两个定点之间的连线段的和的最值,这类问题属于中档题.
10.C
设直线上的点关于点的对称点的坐标为,求出,,再代入直线中即可得到对称直线的方程.
【详解】
设直线上的点关于点的对称点的坐标为,
所以,,所以,,
将其代入直线中,得到,化简得,
故选:C.
本题主要考查的知识要点:直线的方程和中点坐标公式,属于基础题.
11.B
直接代入点到直线距离公式,即可得解.
【详解】
根据距离公式可得:
点到直线的距离,
故选:B.
12.D
求出圆心关于的对称点为,则的最小值是.
【详解】
解:圆的圆心,半径为 ,圆,圆心,半径为,
圆心关于的对称点为,
解得故
.
故选.
本题考查圆的方程,考查点线对称,考查学生分析解决问题的能力,属于基础题.
13.
化简直线为,结合两平行线间的距离公式,即可求解.
【详解】
化简直线为,
根据平行线间的距离公式,可得,
即直线与直线之间的距离为.
故答案为:.
14.或
由直线平行可设,根据距离之比即可得关于的方程,从而可求出直线l的方程.
【详解】
解:由题意知,直线的方程可转化为.易知,
所以可设直线l的方程为(且).
由题意,可得,解得或.
故直线l的方程为或,
即或.
故答案为: 或.
本题考查了直线间的距离公式,属于基础题.设出适合的直线方程是解本题的关键.
15.或
求出的距离,利用三角形的面积求出到直线的距离,求出的方程,结合点在直线上,利用点到直线的距离公式求出的坐标.
【详解】
设点到直线的距离为,
由题意知:,
,
直线的方程为,即,
点在直线上,
设,
,
或,
的坐标为或,故答案为或.
本题主要考查点到直线距离公式以及直线的两点式方程的应用,意在考查计算能力以及函数与方程思想的应用,属于中档题.
16.和
先由两平行直线的距离公式得直线与的距离为,再结合直线被两平行线所截得的线段的长为,求得该直线与直线所成角,然后结合直线的倾斜角为求解即可.
【详解】
解:由两平行直线的距离公式可得:
直线与的距离为,
又直线被两平行线与所截得的线段的长为,
即该直线与直线所成角,
又直线的倾斜角为,
则该直线的倾斜角大小为和,
故答案为:和.
本题考查了两平行直线的距离公式及直线的倾斜角,重点考查了运算能力,属基础题.
17.(1);(2)或.
(1)由与的距离是,代入两条平行直线间的距离公式,可得一个关于的方程,解方程即可求的值;
(2)求出交点坐标,设出直线方程,利用点到直线的距离公式求解即可.
【详解】
解:(1)即,
与的距离.
.
,.
(2)直线与的交点,由:,解得所以交点坐标.
当直线的斜率存在时,设所求的直线方程为:,即:.
点到直线的距离为3,
可得:,
解得,
所求直线方程.
当直线的斜率不存在时,,满足题意.
所求直线方程为:或.
本题考查直线方程的求法,直线的交点坐标,平行线之间的距离的求法,考查计算能力,属于中档题.
18.
直接利用距离公式计算可得;
【详解】
解:点到直线的距离
19.(1);(2);(3).
(1)根据直线,得到,再根据斜率与倾斜角的关系求解.
(2)根据直线,令得,再求解.
(3)根据直线与直线平行,则有求解,然后根据两平行直线间的距离公式求解.
【详解】
(1)因为直线,
所以,
又因为直线的倾斜角为,
所以,
解得.
(2)因为直线,
令得,,
解得.
(3)因为直线与直线平行,
所以,解得,
所以直线,
两平行直线与之间的距离 .
本题主要考查正弦得倾斜角,斜率,截距以及两直线的位置关系,还考查了运算求解的能力,属于中档题.
20.(1);(2)① ;②或.
(1)由,,即可求出直线的斜率,由点斜式即可写出直线的方程;
(2)选①由对称点的性质即可求出;
选②设出点的坐标,由两点间的距离公式列出方程,解出的值,根据、点的坐标即可求出直线的方程.
【详解】
解:(1)因为直线的斜率为,
所以直线的方程为:,
即直线的方程为:;
(2)问题①:
设的坐标为,则
解得:
点的坐标是;
问题②:
设的坐标为,
,
,
解得:或,
的坐标为或,
直线的方程为或.
方法点睛:求解直线方程时应该注意以下问题:
一是根据斜率求倾斜角,要注意倾斜角的范围;
二是求直线方程时,若不能断定直线是否具有斜率时,应对斜率存在与不存在加以讨论;
三是在用截距式时,应先判断截距是否为0,若不确定,则需分类讨论.
21.水电站建在P(90,0)处电线用料最省.
如图,以河流所在直线为x轴、y轴通过点A,建立平面直角坐标系,再求出点B的坐标,利用对称性求解.
【详解】
解:如图,以河流所在直线为x轴、y轴通过点A,建立平面直角坐标系,
则点A(0,300),B(x,700).
设点B在y轴上的射影为H,则x=|BH|==300,
故点B(300,700).
设点A关于x轴的对称点A′(0,-300),
则直线A′B的斜率k=,直线A′B的方程为y=x-300.
令y=0,得x=90,得点P(90,0),
故水电站建在P(90,0)处电线用料最省.
关键点睛:解答本题有两个关键,其一是:想到利用解析法来求解;其二是,能够利用数形结合利用对称性找到满足题意的位置.
答案第1页,共2页
答案第1页,共2页
