第十九章 一次函数单元测试题(Word版附答案)
文档属性
| 名称 | 第十九章 一次函数单元测试题(Word版附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 16:14:47 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第19章《一次函数》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题.(每题3分,共30分)
1.在平面直角坐标系中,将直线y=3x先向左平移2个单位长度,再向上平移5个单位长度,则平移后的新直线为( )
A.y=3x﹣1 B.y=3x+11 C.y=3x+5 D.y=3x+3
2.一次函数y=(k+3)x+1中,y随x的增大而减小,则k的取值范围是( )
A.k>0 B.k<0 C.k<﹣3 D.k>﹣3
3.函数y=(m+1)x﹣(4m﹣3)的图象在第一、二、四象限,那么m的取值范围是( )
A. B. C.m<﹣1 D.m>﹣1
4.已知一次函数y=kx+b(k≠0),若k b<0,则该函数的图象可能是( )
A.B.C.D.
5.已知正比例函数y=(3k﹣1)x,若y随x的增大而增大,则k的取值范围是( )
A.k<0 B.k>0 C.k< D.k>
6.无论a取何值,关于x的函数y=﹣x+a2+1的图象都不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.已知一次函数y=x+b的图象经过一、二、三象限,则b的值可以是( )
A.﹣2 B.﹣1 C.0 D.2
8.下列函数中,满足y的值随x的值增大而增大的是( )
A.y=﹣2x B.y=3x﹣1 C.y= D.y=x2
9.已知正比例函数y=(2m﹣1)x的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2,那么m的取值范围是( )
A.m< B.m> C.m<0 D.m>0
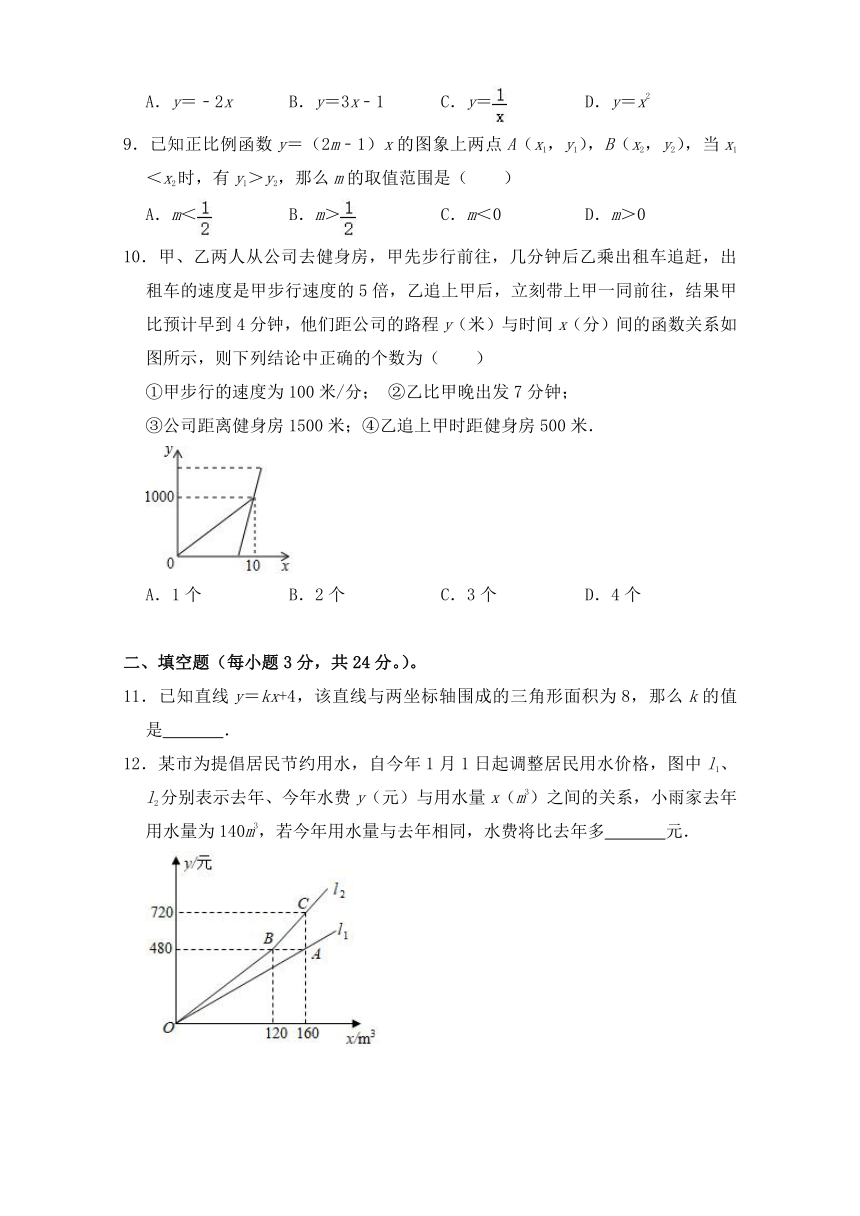
10.甲、乙两人从公司去健身房,甲先步行前往,几分钟后乙乘出租车追赶,出租车的速度是甲步行速度的5倍,乙追上甲后,立刻带上甲一同前往,结果甲比预计早到4分钟,他们距公司的路程y(米)与时间x(分)间的函数关系如图所示,则下列结论中正确的个数为( )
①甲步行的速度为100米/分; ②乙比甲晚出发7分钟;
③公司距离健身房1500米;④乙追上甲时距健身房500米.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共24分。)。
11.已知直线y=kx+4,该直线与两坐标轴围成的三角形面积为8,那么k的值是 .
12.某市为提倡居民节约用水,自今年1月1日起调整居民用水价格,图中l1、l2分别表示去年、今年水费y(元)与用水量x(m3)之间的关系,小雨家去年用水量为140m3,若今年用水量与去年相同,水费将比去年多 元.
13.已知正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置,点A1,A2,A3…在直线y=x+1上,C1,C2,C3…在x轴上,则点A2021的坐标是 .
14.一次函数y=ax+b与正比例函数y=kx在同一平面直角坐标系的图象如图所示,则关于x的不等式ax+b≥kx的解集为 .
15.在平面直角坐标系中,坐标原点O到一次函数y=kx﹣3k+1图象的距离的最大值为 .
16.如图,在平面直角坐标系中,一次函数y=2x﹣2的图象分别交x、y轴于点A、B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是 .
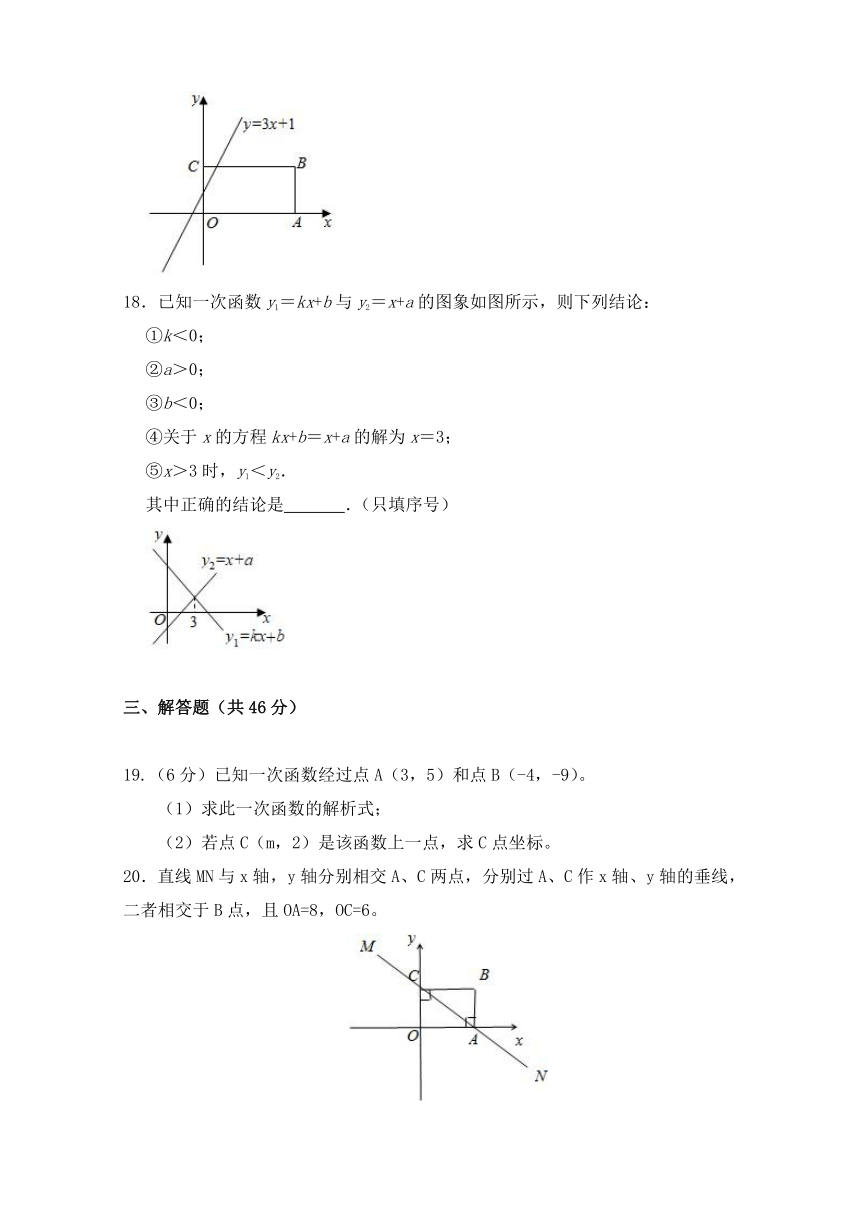
17.如图,在平面直角坐标系中,矩形OABC的点A和点C分别落在x轴和y轴上,AO=4,CO=2,直线y=3x+1以每秒2个单位长度向下移动,经过 秒该直线可将矩形OABC的面积平分.
18.已知一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:
①k<0;
②a>0;
③b<0;
④关于x的方程kx+b=x+a的解为x=3;
⑤x>3时,y1<y2.
其中正确的结论是 .(只填序号)
三、解答题(共46分)
19.(6分)已知一次函数经过点A(3,5)和点B(-4,-9)。
(1)求此一次函数的解析式;
(2)若点C(m,2)是该函数上一点,求C点坐标。
20.直线MN与x轴,y轴分别相交A、C两点,分别过A、C作x轴、y轴的垂线,二者相交于B点,且OA=8,OC=6。
(1)求直线MN的解析式;
(2)已知在直线MN上存在点P,使△PBC是等腰三角形,求点P的坐标。
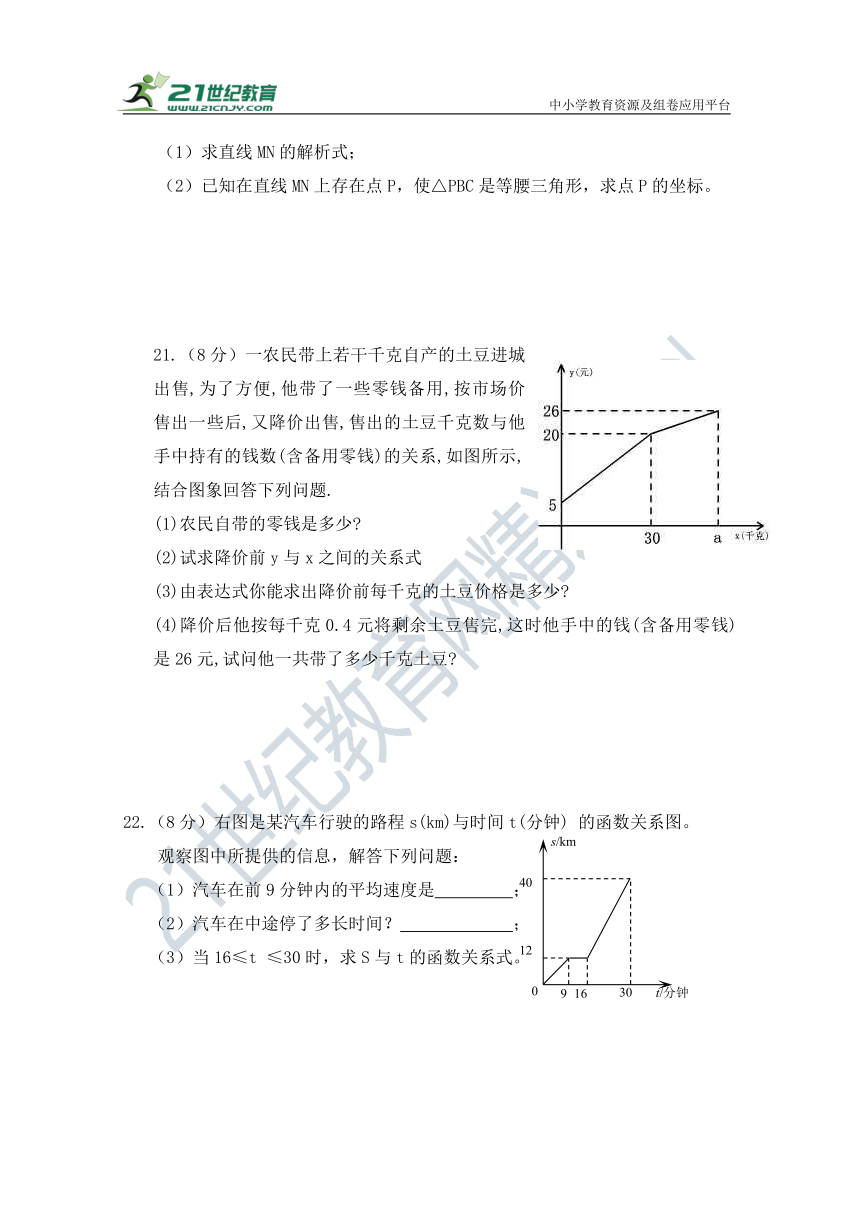
21.(8分)一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆
22.(8分)右图是某汽车行驶的路程s(km)与时间t(分钟) 的函数关系图。
观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是 ;
(2)汽车在中途停了多长时间? ;
(3)当16≤t ≤30时,求S与t的函数关系式。
23.(8分)甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
24.甲、乙两店销售同一种蔬菜种子.在甲店,不论一次购买数量是多少,价格均为4.5元/kg.在乙店价格为5元/kg,如果一次购买2kg以上的种子,超出2kg部分的种子价格打8折.设小明在同一个店一次购买种子的数量为xkg(x>0).
(1)设在甲店花费y1元,在乙店花费y2元,分别求y1,y2关于x的函数解析式;
(2)若小明计划在同一个店将45元全部用于购买这种蔬菜种子,则他在哪个店购买种子的数量较多?
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C C D D B A B C
二、填空题
11.解:∵当x=0时,y=4,
当y=0时,x=﹣,
∴直线与y轴的交点分别为(0,4),与x轴的交点分别为(﹣,0),
∴×4×|﹣|=8,
解得,k=±1,
故答案为:k=±1.
12.解:设当x>120时,l2对应的函数解析式为y=kx+b,
,
解得,
即当x>120时,l2对应的函数解析式为y=6x﹣240,
当x=140时,y=6×140﹣240=600,
由图象可知,去年的水价是480÷160=3(元/m3),故小雨家去年用水量为140m3,需要缴费:140×3=420(元),
600﹣420=180(元),
即小雨家去年用水量为140m3,若今年用水量与去年相同,水费将比去年多180元,
故答案为:180.
13.解:根据条件y=x+1,可以得到该直线与x轴的夹角是45°,且OA1=1,即;
再结合正方形条件,可以判定所有三角形都是等腰直角三角形;
于是A2 的高度是1+1=2,即;
A3的高度是2+2=4,即;
同样A4 的高度是4+4=8,即;
…An 的高度是2n﹣1.
所以当n=2021 时,A2021 的高度是22020,即,
于是将该点的纵坐标代入y=x+1,得到x=22020﹣1.
故答案是:(22020﹣1,22020).
14.解:从图象可看出当x≥﹣1,直线l2的图象在直线l1的上方,不等式ax+b>kx.
故答案为:x≥﹣1.
15.解:y=kx﹣3k+1=k(x﹣3)+1,
即该一次函数经过定点(3,1),
设该定点为P,则P(3,1),
当直线OP与直线y=kx﹣3k+1垂直时,坐标原点O到一次函数y=kx﹣3k+1的距离最大,如下图所示:
最大距离为:=,
故答案为:.
16.解:∵一次函数y=2x﹣2的图象分别交x、y轴于点A、B,
∴令x=0,得y=﹣2,令y=0,则x=1,
∴A(1,0),B(0,﹣2),
∴OA=1,OB=2,
过A作AF⊥AB交BC于F,过F作FE⊥x轴于E,
∵∠ABC=45°,
∴△ABF是等腰直角三角形,
∴AB=AF,
∵∠OAB+∠ABO=∠OAB+∠EAF=90°,
∴∠ABO=∠EAF,
在△ABO和△FAE中
,
∴△ABO≌△FAE(AAS),
∴AE=OB=2,EF=OA=1,
∴F(3,﹣1),
设直线BC的函数表达式为:y=kx+b,
∴,解得,
∴直线BC的函数表达式为:y=x﹣2,
故答案为:y=x﹣2.
17.解:连接AC、BO,交于点D,
当y=3x+1经过D点时,该直线可将 OABC的面积平分;
∵AC,BO是 OABC的对角线,
∴OD=BD,
∵O(0,0),B(4,2),
∴D(2,1),
根据题意设平移后直线的解析式为y=3x+b,
∵D(2,1),
∴1=3×2+b,解得b=﹣5,
∴平移后的直线的解析式为y=3x﹣5,
∴直线y=3x+1要向下平移6个单位,
∴时间为3秒,
故答案为:3.
18.解:∵一次函数y1=kx+b的图象经过一、二、四象限,
∴k<0,b>0,
故①正确,③错误;
∵一次函数y2=x+a的图象经过一、三、四象限,
∴a<0,故②错误;
∵一次函数y1=kx+b与y2=x+a的交点的横坐标为3,
∴关于x的方程kx+b=x+a的解为x=3,故④正确;
由图象可知,当x>3时,y1<y2,故⑤正确;
故正确的结论是①④⑤.
故答案为①④⑤.
三、解答题
19、【答案】(1)设其解析式为y=kx+b(k、b是常数,且k≠0)
则
5=3k+b
9= 4k+b
∴k=2,b= 1;
∴其解析式为y=2x-1
(2)∵点C(m,2)在y=2x-1上
∴2=2m-1
∴m=
∴点C的坐标为(,2)
20.【答案】(1)∵OA=8,OC=6,
∴A(8,0),C(0,6),
设直线MN的解析式为:y=kx+b,
8k+b=0
b=6,
解得:
k= ,b=6,
直线MN的解析式:y=- x+6;
(2)由题意得,B(8,6),
∵点P在直线MN上,
∴设P(a,-a+6),
当PC=PB时,点P为BC的中垂线与MN的交点,则P1(4,3);
当PC=BC时,a2+(- a+6-6)2=64,
解得,a1= - ,a2= ,
则P2(- ,),P3(,);
当PB=BC时,(a-8)2+(-a+6-6)2=64,
解得,a= ,
则P4(,-)。
21、(1)5元 (2)y=0.5x+5 (3) 0.5元/㎏,(4)40㎏
22、(1)80km/h;(2)7分钟;(3)S=2t-20
23、解:(1)由图象可得,
货车的速度为300÷5=60(千米/小时),
则轿车到达乙地时,货车与甲地的距离是60×4.5=270(千米),
即轿车到达乙地时,货车与甲地的距离是270千米;
(2)设线段CD对应的函数表达式是y=kx+b,
∵点C(2.5,80),点D(4.5,300),
∴,
解得,
即线段CD对应的函数表达式是y=110x﹣195(2.5≤x≤4.5);
(3)当x=2.5时,两车之间的距离为:60×2.5﹣80=70,
∵70>15,
∴在轿车行进过程,两车相距15千米时间是在2.5~4.5之间,
由图象可得,线段OA对应的函数解析式为y=60x,
则|60x﹣(110x﹣195)|=15,
解得x1=3.6,x2=4.2,
∵轿车比货车晚出发1.5小时,3.6﹣1.5=2.1(小时),4.2﹣1.5=2.7(小时),
∴在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米,
答:在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米.
24.解:(1)由题意可得,y1=4.5x,
当0≤x≤2时,y2=5x,
当x>2时,y2=5×2+(x﹣2)×5×0.8=4x+2,
(2)当y=45时,
在甲店中,45=4.5x,得x=10,
在乙店中,45=4x+2,得x=10.75,
∵10<10.75,
∴在乙店购买的数量较多.
0
9
16
30
t/分钟
s/km
40
12
第19章《一次函数》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题.(每题3分,共30分)
1.在平面直角坐标系中,将直线y=3x先向左平移2个单位长度,再向上平移5个单位长度,则平移后的新直线为( )
A.y=3x﹣1 B.y=3x+11 C.y=3x+5 D.y=3x+3
2.一次函数y=(k+3)x+1中,y随x的增大而减小,则k的取值范围是( )
A.k>0 B.k<0 C.k<﹣3 D.k>﹣3
3.函数y=(m+1)x﹣(4m﹣3)的图象在第一、二、四象限,那么m的取值范围是( )
A. B. C.m<﹣1 D.m>﹣1
4.已知一次函数y=kx+b(k≠0),若k b<0,则该函数的图象可能是( )
A.B.C.D.
5.已知正比例函数y=(3k﹣1)x,若y随x的增大而增大,则k的取值范围是( )
A.k<0 B.k>0 C.k< D.k>
6.无论a取何值,关于x的函数y=﹣x+a2+1的图象都不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.已知一次函数y=x+b的图象经过一、二、三象限,则b的值可以是( )
A.﹣2 B.﹣1 C.0 D.2
8.下列函数中,满足y的值随x的值增大而增大的是( )
A.y=﹣2x B.y=3x﹣1 C.y= D.y=x2
9.已知正比例函数y=(2m﹣1)x的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2,那么m的取值范围是( )
A.m< B.m> C.m<0 D.m>0
10.甲、乙两人从公司去健身房,甲先步行前往,几分钟后乙乘出租车追赶,出租车的速度是甲步行速度的5倍,乙追上甲后,立刻带上甲一同前往,结果甲比预计早到4分钟,他们距公司的路程y(米)与时间x(分)间的函数关系如图所示,则下列结论中正确的个数为( )
①甲步行的速度为100米/分; ②乙比甲晚出发7分钟;
③公司距离健身房1500米;④乙追上甲时距健身房500米.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共24分。)。
11.已知直线y=kx+4,该直线与两坐标轴围成的三角形面积为8,那么k的值是 .
12.某市为提倡居民节约用水,自今年1月1日起调整居民用水价格,图中l1、l2分别表示去年、今年水费y(元)与用水量x(m3)之间的关系,小雨家去年用水量为140m3,若今年用水量与去年相同,水费将比去年多 元.
13.已知正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置,点A1,A2,A3…在直线y=x+1上,C1,C2,C3…在x轴上,则点A2021的坐标是 .
14.一次函数y=ax+b与正比例函数y=kx在同一平面直角坐标系的图象如图所示,则关于x的不等式ax+b≥kx的解集为 .
15.在平面直角坐标系中,坐标原点O到一次函数y=kx﹣3k+1图象的距离的最大值为 .
16.如图,在平面直角坐标系中,一次函数y=2x﹣2的图象分别交x、y轴于点A、B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是 .
17.如图,在平面直角坐标系中,矩形OABC的点A和点C分别落在x轴和y轴上,AO=4,CO=2,直线y=3x+1以每秒2个单位长度向下移动,经过 秒该直线可将矩形OABC的面积平分.
18.已知一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:
①k<0;
②a>0;
③b<0;
④关于x的方程kx+b=x+a的解为x=3;
⑤x>3时,y1<y2.
其中正确的结论是 .(只填序号)
三、解答题(共46分)
19.(6分)已知一次函数经过点A(3,5)和点B(-4,-9)。
(1)求此一次函数的解析式;
(2)若点C(m,2)是该函数上一点,求C点坐标。
20.直线MN与x轴,y轴分别相交A、C两点,分别过A、C作x轴、y轴的垂线,二者相交于B点,且OA=8,OC=6。
(1)求直线MN的解析式;
(2)已知在直线MN上存在点P,使△PBC是等腰三角形,求点P的坐标。
21.(8分)一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆
22.(8分)右图是某汽车行驶的路程s(km)与时间t(分钟) 的函数关系图。
观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是 ;
(2)汽车在中途停了多长时间? ;
(3)当16≤t ≤30时,求S与t的函数关系式。
23.(8分)甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
24.甲、乙两店销售同一种蔬菜种子.在甲店,不论一次购买数量是多少,价格均为4.5元/kg.在乙店价格为5元/kg,如果一次购买2kg以上的种子,超出2kg部分的种子价格打8折.设小明在同一个店一次购买种子的数量为xkg(x>0).
(1)设在甲店花费y1元,在乙店花费y2元,分别求y1,y2关于x的函数解析式;
(2)若小明计划在同一个店将45元全部用于购买这种蔬菜种子,则他在哪个店购买种子的数量较多?
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C C D D B A B C
二、填空题
11.解:∵当x=0时,y=4,
当y=0时,x=﹣,
∴直线与y轴的交点分别为(0,4),与x轴的交点分别为(﹣,0),
∴×4×|﹣|=8,
解得,k=±1,
故答案为:k=±1.
12.解:设当x>120时,l2对应的函数解析式为y=kx+b,
,
解得,
即当x>120时,l2对应的函数解析式为y=6x﹣240,
当x=140时,y=6×140﹣240=600,
由图象可知,去年的水价是480÷160=3(元/m3),故小雨家去年用水量为140m3,需要缴费:140×3=420(元),
600﹣420=180(元),
即小雨家去年用水量为140m3,若今年用水量与去年相同,水费将比去年多180元,
故答案为:180.
13.解:根据条件y=x+1,可以得到该直线与x轴的夹角是45°,且OA1=1,即;
再结合正方形条件,可以判定所有三角形都是等腰直角三角形;
于是A2 的高度是1+1=2,即;
A3的高度是2+2=4,即;
同样A4 的高度是4+4=8,即;
…An 的高度是2n﹣1.
所以当n=2021 时,A2021 的高度是22020,即,
于是将该点的纵坐标代入y=x+1,得到x=22020﹣1.
故答案是:(22020﹣1,22020).
14.解:从图象可看出当x≥﹣1,直线l2的图象在直线l1的上方,不等式ax+b>kx.
故答案为:x≥﹣1.
15.解:y=kx﹣3k+1=k(x﹣3)+1,
即该一次函数经过定点(3,1),
设该定点为P,则P(3,1),
当直线OP与直线y=kx﹣3k+1垂直时,坐标原点O到一次函数y=kx﹣3k+1的距离最大,如下图所示:
最大距离为:=,
故答案为:.
16.解:∵一次函数y=2x﹣2的图象分别交x、y轴于点A、B,
∴令x=0,得y=﹣2,令y=0,则x=1,
∴A(1,0),B(0,﹣2),
∴OA=1,OB=2,
过A作AF⊥AB交BC于F,过F作FE⊥x轴于E,
∵∠ABC=45°,
∴△ABF是等腰直角三角形,
∴AB=AF,
∵∠OAB+∠ABO=∠OAB+∠EAF=90°,
∴∠ABO=∠EAF,
在△ABO和△FAE中
,
∴△ABO≌△FAE(AAS),
∴AE=OB=2,EF=OA=1,
∴F(3,﹣1),
设直线BC的函数表达式为:y=kx+b,
∴,解得,
∴直线BC的函数表达式为:y=x﹣2,
故答案为:y=x﹣2.
17.解:连接AC、BO,交于点D,
当y=3x+1经过D点时,该直线可将 OABC的面积平分;
∵AC,BO是 OABC的对角线,
∴OD=BD,
∵O(0,0),B(4,2),
∴D(2,1),
根据题意设平移后直线的解析式为y=3x+b,
∵D(2,1),
∴1=3×2+b,解得b=﹣5,
∴平移后的直线的解析式为y=3x﹣5,
∴直线y=3x+1要向下平移6个单位,
∴时间为3秒,
故答案为:3.
18.解:∵一次函数y1=kx+b的图象经过一、二、四象限,
∴k<0,b>0,
故①正确,③错误;
∵一次函数y2=x+a的图象经过一、三、四象限,
∴a<0,故②错误;
∵一次函数y1=kx+b与y2=x+a的交点的横坐标为3,
∴关于x的方程kx+b=x+a的解为x=3,故④正确;
由图象可知,当x>3时,y1<y2,故⑤正确;
故正确的结论是①④⑤.
故答案为①④⑤.
三、解答题
19、【答案】(1)设其解析式为y=kx+b(k、b是常数,且k≠0)
则
5=3k+b
9= 4k+b
∴k=2,b= 1;
∴其解析式为y=2x-1
(2)∵点C(m,2)在y=2x-1上
∴2=2m-1
∴m=
∴点C的坐标为(,2)
20.【答案】(1)∵OA=8,OC=6,
∴A(8,0),C(0,6),
设直线MN的解析式为:y=kx+b,
8k+b=0
b=6,
解得:
k= ,b=6,
直线MN的解析式:y=- x+6;
(2)由题意得,B(8,6),
∵点P在直线MN上,
∴设P(a,-a+6),
当PC=PB时,点P为BC的中垂线与MN的交点,则P1(4,3);
当PC=BC时,a2+(- a+6-6)2=64,
解得,a1= - ,a2= ,
则P2(- ,),P3(,);
当PB=BC时,(a-8)2+(-a+6-6)2=64,
解得,a= ,
则P4(,-)。
21、(1)5元 (2)y=0.5x+5 (3) 0.5元/㎏,(4)40㎏
22、(1)80km/h;(2)7分钟;(3)S=2t-20
23、解:(1)由图象可得,
货车的速度为300÷5=60(千米/小时),
则轿车到达乙地时,货车与甲地的距离是60×4.5=270(千米),
即轿车到达乙地时,货车与甲地的距离是270千米;
(2)设线段CD对应的函数表达式是y=kx+b,
∵点C(2.5,80),点D(4.5,300),
∴,
解得,
即线段CD对应的函数表达式是y=110x﹣195(2.5≤x≤4.5);
(3)当x=2.5时,两车之间的距离为:60×2.5﹣80=70,
∵70>15,
∴在轿车行进过程,两车相距15千米时间是在2.5~4.5之间,
由图象可得,线段OA对应的函数解析式为y=60x,
则|60x﹣(110x﹣195)|=15,
解得x1=3.6,x2=4.2,
∵轿车比货车晚出发1.5小时,3.6﹣1.5=2.1(小时),4.2﹣1.5=2.7(小时),
∴在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米,
答:在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米.
24.解:(1)由题意可得,y1=4.5x,
当0≤x≤2时,y2=5x,
当x>2时,y2=5×2+(x﹣2)×5×0.8=4x+2,
(2)当y=45时,
在甲店中,45=4.5x,得x=10,
在乙店中,45=4x+2,得x=10.75,
∵10<10.75,
∴在乙店购买的数量较多.
0
9
16
30
t/分钟
s/km
40
12
