4.3指数函数与对数函数的关系 课件(共20张PPT)
文档属性
| 名称 | 4.3指数函数与对数函数的关系 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 763.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
指数函数与对数函数的关系
温故知新
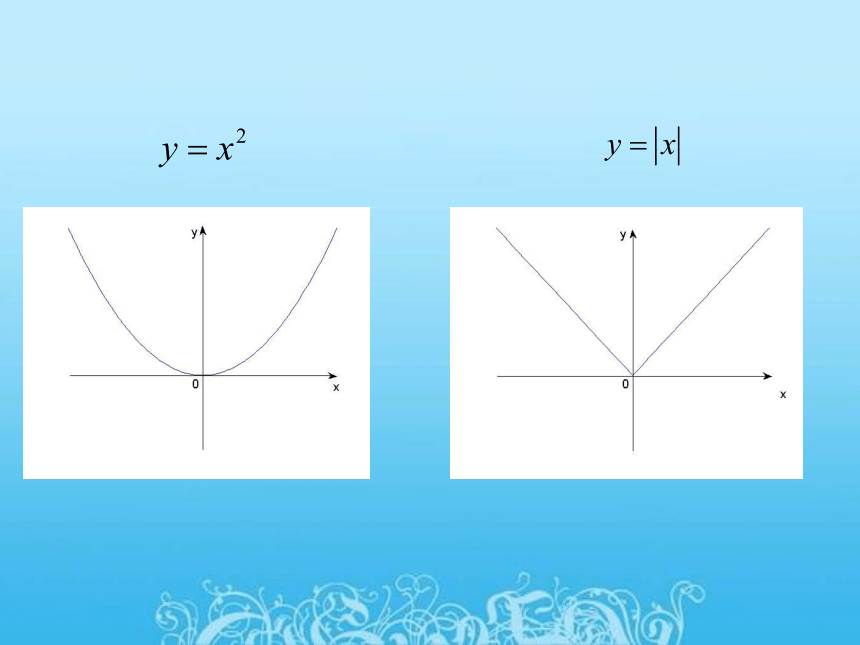
1、指数函数 的图象
2、对数函数 的图象
问题1:
指数函数y=ax与对数函数y=loga x(a>0,a≠1)有什么关系
称这两个函数互为反函数
y=ax
x=loga y
y=loga x
指数换对数
交换x,y
y=3x+5
交换x,y
移项
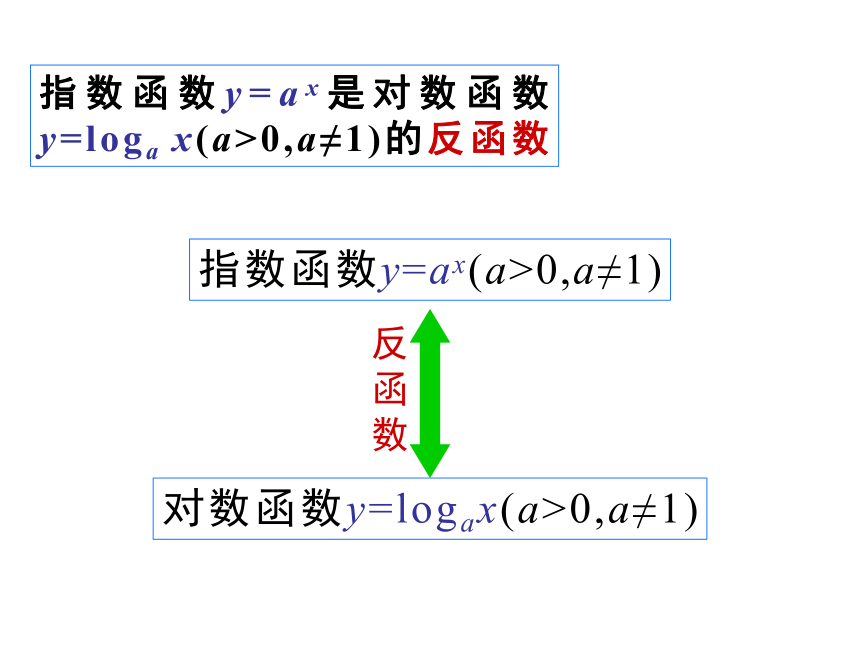
指数函数y=ax(a>0,a≠1)
对数函数y=logax(a>0,a≠1)
反函数
指数函数y=ax是对数函数y=loga x(a>0,a≠1)的反函数
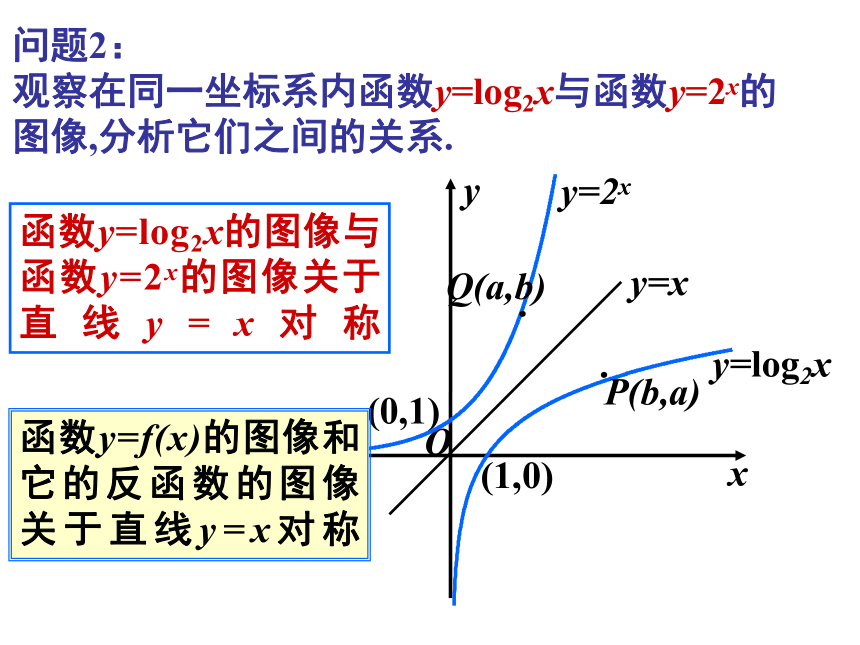
问题2:
观察在同一坐标系内函数y=log2x与函数y=2x的图像,分析它们之间的关系.
函数y=log2x的图像与函数y=2x的图像关于直线y=x对称
(1,0)
(0,1)
O
x
y
y=log2x
y=2x
y=x
P(b,a)
Q(a,b)
函数y=f(x)的图像和它的反函数的图像关于直线y=x对称
.
.
反函数定义
当一个函数是一一映射时,可以把这个函数的因变量作为一个新的函数的自变量,而把这个函数的自变量作为新的函数的因变量,称这两个函数互为反函数。
说明:
① 函数必须是一一映射,反函数亦是函数。
② 原函数的定义域是其反函数的值域,
原函数的值域是其反函数的定义域。
数通常用 表示。
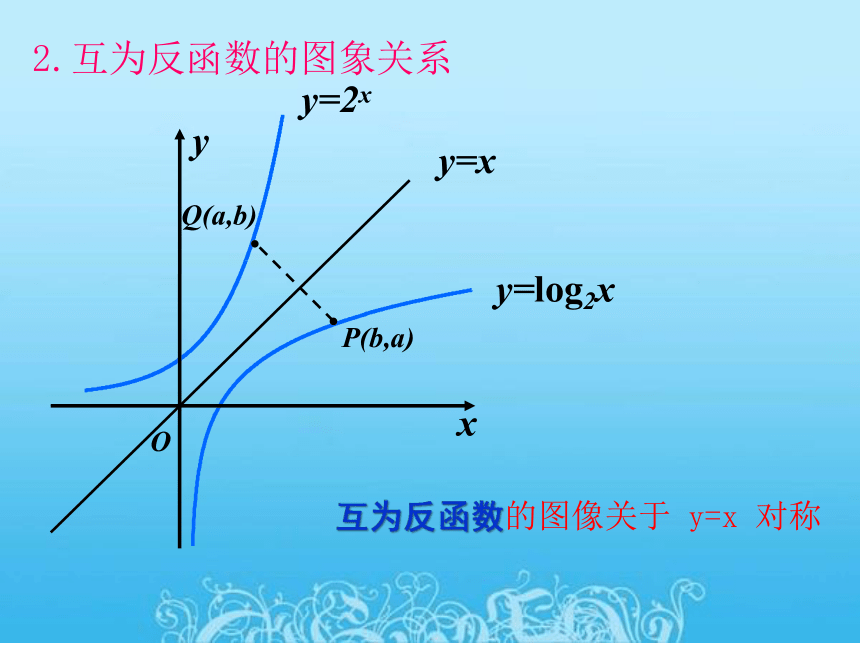
2.互为反函数的图象关系
y=log2x
y=2x
y=x
P(b,a)
Q(a,b)
O
x
y
互为反函数的图像关于 y=x 对称
3.比较这两个函数增长的差异
O
x
y
y=log2x
y=2x
●
●
●
●
△x
△y
△y
△x
●
●
●
特点:1、在区间 指数函数随x增长函数值增长速度逐步加快,对数函数随x增长函数值增长速度变的缓慢。
2、互为反函数的两个函数在公共定义域上单调性一致
例1 写出下列对数函数的反函数:
(1)y =lgx;
解(1)
y=10x
(2)
x、y互换得反函数
x、y互换得反函数
例2 写出下列指数函数的反函数:
(1) y=5x
答案:
(1)
(2)
例3 求函数y=3x-2(x>0)反函数,并在同一直角坐标系中作出函数及其反函数的图象。
解:由y=3x-2(x>-1 )得 (y>-2 )
所以y=3x-2(x∈R)的反函数是
(x>-2 )
y=3x-2 经过两点(0,-2), (2/3,0)
经过两点(-2,0), (0 ,2/3 )
做一做
0
x
y
y=3x-2
y=x
求函数反函数的步骤:
3. 求原函数的值域
1. 反解
2. x与y互换
4. 写出反函数及它的定义域
b=f(a)
a=f-1(b)
点(b,a)在反函数y=f-1(x) 的图像上
点(a,b)在函数y=f(x)的图像上
(1,0)
(0,1)
O
x
y
y=log2x
y=2x
y=x
P(b,a)
Q(a,b)
结论:
例4 函数f(x)=loga (x-1)(a>0且a≠1)的反函数的图象
经过点(1, 4),求a的值。
解:依题意,原函数经过点(4,1)得
b=f(a)
a=f-1(b)
点(b,a)在反函数y=f-1(x) 的图像上
点(a,b)在函数y=f(x)的图像上
b=f(a)
a=f-1(b)
点(b,a)在反函数y=f-1(x) 的图像上
点(a,b)在函数y=f(x)的图像上
巩固练习
已知函数 ,其反函数 ,则函数
的图象是( )
y
x
0
y
x
0
y
x
0
y
x
0
●
●
●
●
●
●
1
2
1
2
●
1
0.5
●
1
0.5
(A)
(C)
(B)
(D)
A
变式训练:
的图象是( )
C
今天有哪些收获?
1、 与 互为反函数。
2、互为反函数的图象关于直线 y=x 对称。
4、数形结合的思想。
3、 原函数的定义域是其反函数的值域,
原函数的值域是其反函数的定义域。
指数函数与对数函数的关系
温故知新
1、指数函数 的图象
2、对数函数 的图象
问题1:
指数函数y=ax与对数函数y=loga x(a>0,a≠1)有什么关系
称这两个函数互为反函数
y=ax
x=loga y
y=loga x
指数换对数
交换x,y
y=3x+5
交换x,y
移项
指数函数y=ax(a>0,a≠1)
对数函数y=logax(a>0,a≠1)
反函数
指数函数y=ax是对数函数y=loga x(a>0,a≠1)的反函数
问题2:
观察在同一坐标系内函数y=log2x与函数y=2x的图像,分析它们之间的关系.
函数y=log2x的图像与函数y=2x的图像关于直线y=x对称
(1,0)
(0,1)
O
x
y
y=log2x
y=2x
y=x
P(b,a)
Q(a,b)
函数y=f(x)的图像和它的反函数的图像关于直线y=x对称
.
.
反函数定义
当一个函数是一一映射时,可以把这个函数的因变量作为一个新的函数的自变量,而把这个函数的自变量作为新的函数的因变量,称这两个函数互为反函数。
说明:
① 函数必须是一一映射,反函数亦是函数。
② 原函数的定义域是其反函数的值域,
原函数的值域是其反函数的定义域。
数通常用 表示。
2.互为反函数的图象关系
y=log2x
y=2x
y=x
P(b,a)
Q(a,b)
O
x
y
互为反函数的图像关于 y=x 对称
3.比较这两个函数增长的差异
O
x
y
y=log2x
y=2x
●
●
●
●
△x
△y
△y
△x
●
●
●
特点:1、在区间 指数函数随x增长函数值增长速度逐步加快,对数函数随x增长函数值增长速度变的缓慢。
2、互为反函数的两个函数在公共定义域上单调性一致
例1 写出下列对数函数的反函数:
(1)y =lgx;
解(1)
y=10x
(2)
x、y互换得反函数
x、y互换得反函数
例2 写出下列指数函数的反函数:
(1) y=5x
答案:
(1)
(2)
例3 求函数y=3x-2(x>0)反函数,并在同一直角坐标系中作出函数及其反函数的图象。
解:由y=3x-2(x>-1 )得 (y>-2 )
所以y=3x-2(x∈R)的反函数是
(x>-2 )
y=3x-2 经过两点(0,-2), (2/3,0)
经过两点(-2,0), (0 ,2/3 )
做一做
0
x
y
y=3x-2
y=x
求函数反函数的步骤:
3. 求原函数的值域
1. 反解
2. x与y互换
4. 写出反函数及它的定义域
b=f(a)
a=f-1(b)
点(b,a)在反函数y=f-1(x) 的图像上
点(a,b)在函数y=f(x)的图像上
(1,0)
(0,1)
O
x
y
y=log2x
y=2x
y=x
P(b,a)
Q(a,b)
结论:
例4 函数f(x)=loga (x-1)(a>0且a≠1)的反函数的图象
经过点(1, 4),求a的值。
解:依题意,原函数经过点(4,1)得
b=f(a)
a=f-1(b)
点(b,a)在反函数y=f-1(x) 的图像上
点(a,b)在函数y=f(x)的图像上
b=f(a)
a=f-1(b)
点(b,a)在反函数y=f-1(x) 的图像上
点(a,b)在函数y=f(x)的图像上
巩固练习
已知函数 ,其反函数 ,则函数
的图象是( )
y
x
0
y
x
0
y
x
0
y
x
0
●
●
●
●
●
●
1
2
1
2
●
1
0.5
●
1
0.5
(A)
(C)
(B)
(D)
A
变式训练:
的图象是( )
C
今天有哪些收获?
1、 与 互为反函数。
2、互为反函数的图象关于直线 y=x 对称。
4、数形结合的思想。
3、 原函数的定义域是其反函数的值域,
原函数的值域是其反函数的定义域。
